次二次哈密尔顿系统周期解的存在性问题

张小静，郭 飞

(天津大学 理学院 数学系，天津 300072)

次二次哈密尔顿系统周期解的存在性问题

张小静，郭 飞

(天津大学 理学院 数学系，天津 300072)

用极大极小原理证明了次二次哈密尔顿系统的周期解的存在性结果.

周期解；哈密尔顿系统；次二次条件；极大极小方法；变分原理

本文考虑以下次二次Hamilton系统的周期边值问题：

(1)

我们知道有好多诸如系统(1)的周期解的研究情况，包括存在性和多重性等情况.本文将讨论周期为T的系统(1.1)的周期解，且H(t,z)是次二次的，即当|z|→+∞时H(z)的增长速度慢于|z|2.文献[3-9]讨论了次二次Hamilton系统周期解的情况.文献[3]中的Hamilton系统H(t,z)和文献[4]中的H(z)需要满足凸的条件.文献[7]和[10]中，要求Hamilton系统函数H(t,z)是可微的. 文献[8]和[9] 中，黑塞矩阵Hzz(t,z)是有界的.

文献[1] 利用极大极小值原理证明了超二次自制 Hamilton 系统周期解的存在性.本文中，我们要求H(t,z)是可微的且满足别的条件, 则可以利用文献 [1] 提供的极大极小值方法证明存在性.

我们用|·|和(·，·)表示R2n中的标准范数和内积.

本文分为三部分，我们将在第二节中给出一些将会在第三节中用到的预备知识.

在第三节，我们假设H∈C1(R2n,R)满足条件 (H1)-(H4)，即

(H1)H(t+T,z)=H(t,z),∀z∈R2n,∀t∈R

(H2) 存在常数a≥0，使得|▽H(t,z)|≤φ(|z|),|z|>a,∀t∈R其中φ∈C(R+,R+)(R+[0,+∞))满足：

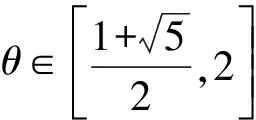
(▽H(t,z),z)≥-b|z|θ-K0,∀z∈R2n,∀t∈R

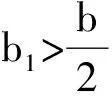
那么(1)至少存在一个解.

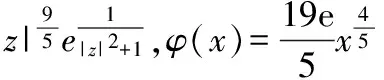
定理1 设H∈C1(R×R2n,R)满足 (H1), (H2), (H3) 及 (H4)， 那么系统(1)至少存在一个周期解.

1 预备知识

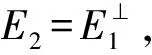
Γ{Φ∈C([0,1]×E,E)|Φ(0,u)=u且P2Φ(t,u)=P2u-K(t,u),其中K：[0，1]×E→E2是紧映射}

定义1 如果对于任意集合Φ∈Γ，以及任意t∈[0,1]，Φ(t,∂Q)∩S=φ,我们有Φ(t,Q)∩S≠φ,∀t∈[0,1]，则称S和∂Q环绕.

引理1[1]设E是一个希尔伯特空间，E1,E2是E的两个直和子空间，E=E1⊕E2.如果I∈C1(E,R)满足(P.S.)条件，且满足以下条件：

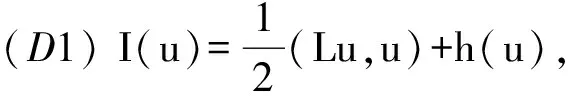
(D2)h′是紧算子,

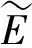
(I)S⊂E1,I|S≥α,

(II)Q有界，且I|∂Q≤β,

(III)S和∂Q环绕，

那么泛函I有一个临界值c≥α.

引理 2[5]对每个r∈[1,+∞],E紧嵌入到Lr([0,T],R2n).特别地, 存在Cr>0使得

‖zr‖≤Cr‖z‖，∀z∈E

(2)

设S1=R/TZ，我们定义两个空间如下：

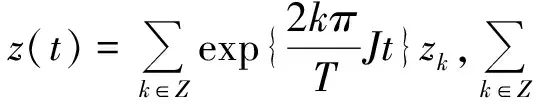
和

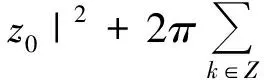
设算子A∈L(E)，及空间E上的泛函I1为：

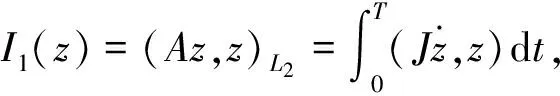
其中：L(E)为E上的所有线性算子构成的集合.于是我们有E的特征子空间

εk=

其中{e1,e2,…e2n}是R2n上的一组标准基.显然的，

E0=span{e1,e2,…,e2n}

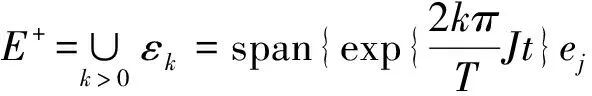
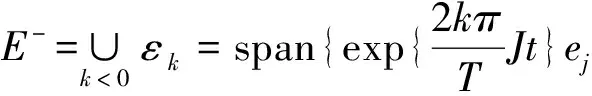
因此，每个z∈E都有惟一分解z=z++z-+z0.对u=u+u-+u0和v=v+v-+v0，我们容易验证〈u,v〉B[u-,v-]-B[u-,v-]+(u0,v0)是E上的内积.以上这些说明‖z‖2〈z,z〉=(Az+,z+)L2-(Az-,z-)L2+|z0|2为空间E上的等价范数.所以，在后面的讨论中，我们都采用这种范数作为空间E上的范数.通过上面的表述，我们知道E+，E-和E0关于相应的内积是相互正交的.另外，可以证得A∈L(E)是自伴算子，即(Au,v)L2=(u,Av)L2.

2 利用极大极小值方法证明

由条件(φ)，我们知道存在常数M0>0, 使得

φ(x)≤x+M0,∀x∈R+

(3)

因为H∈C1(R×R2n,R) ，▽H∈C(R×R2n，R2n)所以存在常数a0>0使得

|▽H(t,z)|≤a0,∀t∈[0,T],∀z∈R2n且|z|≤a

(4)

于是由条件(H1) 和 (H2)， 我们有

|▽H(t,z)|≤φ(|z|)+a0,∀t∈R∀z∈R2n

(5)

从而根据条件(φ)，我们得到

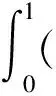
也就是说，

|H(t,z)|≤φ(|z|)|z|+a0|z|+a1,∀t∈[0,T],∀z∈R2n

(6)

其中a1=max{|H(t,0)|t∈[0,T]}≥0是常数.

由不等式(3)和条件(H1) 可得

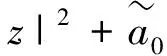
(7)

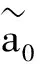
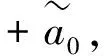
(8)

[1] 的命题B.37，可知h∈C1(E,R)且h′是紧的.

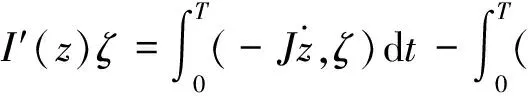
显然I在E上的临界点即是系统(1)的一个弱解.

如上所述，我们定义

令g(z)=-I(z)，则g∈C1(E,R).

第一步.g(z)满足 (P.S.) 条件

证明:设{zm}是E中的任意一组序列满足{g(zm)}有界，且当m→+∞时g′(zm)→0.

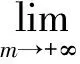
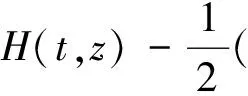
(9)

其中a2>0是一个足够大的常数.

因为{g(zm)}有界，存在常数M1>0使得|g(zm)|≤M1，∀m∈N又因为m→+∞时g′(zm)→0，所以对m∈N充分大，由式(9)可知

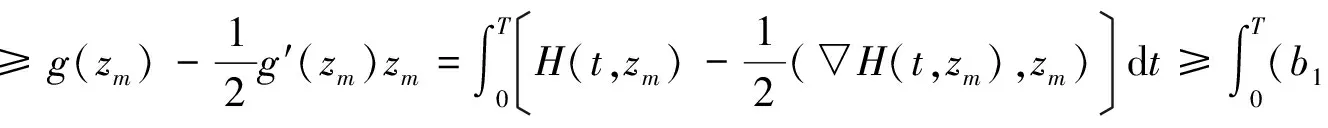
(10)

即

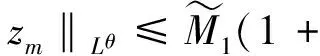
(11)

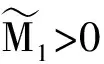
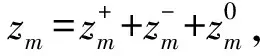
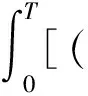
(12)

由式(8)，Hölder不等式及引理2可知

(13)

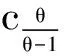
根据式(11)、(13)，有

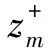
(14)

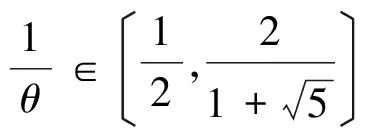
(15)

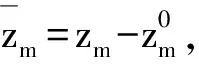
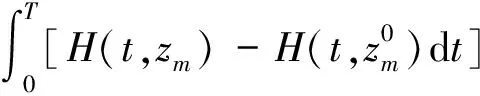
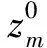
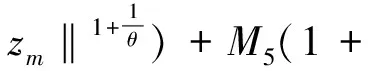
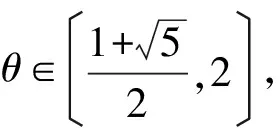
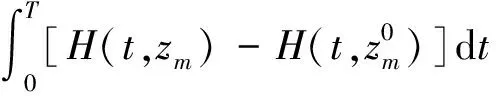
(16)

另外，

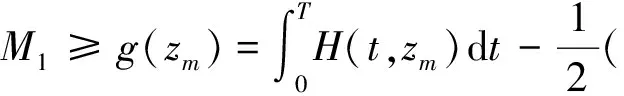
则由式(14)、(16)，有

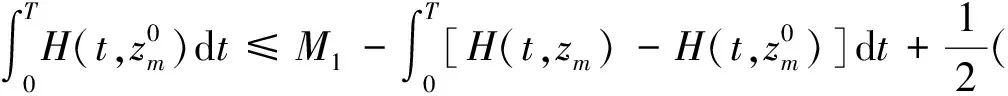
(17)

另一方面，不等式(9)和条件 (H3) 表明

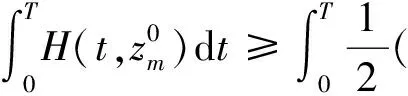
(18)

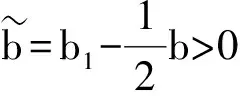
(19)

其中M8>0是常数.

结合不等式(19)和不等式(14)，(15)考虑，我们有

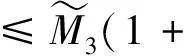
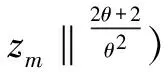
(20)

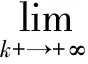
其次，我们将证明{zm}有一个收敛子列.

为了说明{zm}在E中是列紧的，注意到

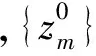
由简单的计算可知∓P±g′(z)=z±∓P±h′(z),∀z∈E其中P±是E到E±中的正交投影，且h′是紧的.因此，有

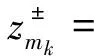
(21)

因为h′是紧的，有一个收敛子列h′(zmkj) ，另外j→+∞时,g′(zmkj)→0 ， 所以{zm}有一个收敛子列.

第二步 g满足引理 1 中的 (D1) 和 (D3) 条件.

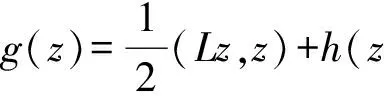
接下来验证g满足引理1中的 (D3) 条件.

Ⅰ 令S≜E1=E-⊕E0则需要证明存在常数α>0使得当z∈S时，g(z)≥α.

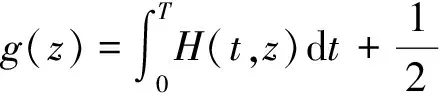
即

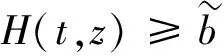
(22)

因此，若,z∈S

(23)

我们完成了Ⅰ的证明.

Ⅱ 我们将证明存在常数β<α使得在∂Q上，g(z)≤β，其中Q=E+∩BR⊂E2,R>0 (我们稍后给出R的定义).

若z∈Q，由式(6)可知

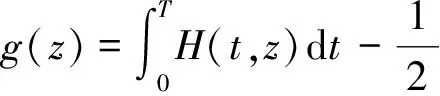
(24)

对给定的δ>0，由条件(φ)知，存在常数G(δ)>0使得

φ(x)<δx,∀x>G(δ)

(25)

令G1(z)={t∈[0,T]||z(t)>G(δ)|}和G2(z)={t∈[0,T]||z(t)≤G(δ)|}，则

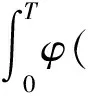
(26)

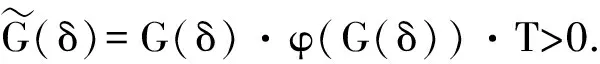
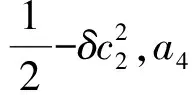
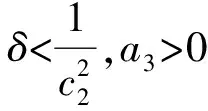
Ⅲ验证S和∂Q环绕.

令P1,P2是E到其给定子空间E1,E2上的投影，

Γ={Φ∈C([0,1]×E,E)|Φ(0,u)=u且P2Φ(t,u)=P2u-K(t,u),其中K：[0，1]×E→E是紧映射.}

若

Φ(t,∂Q)∩S=φ，∀t∈[0,1]

(28)

我们断言Φ(t,Q)∩S≠φ，∀t∈[0,1]，即存在z(t)∈Q使得P2Φ(t,z(t))=0. 对u∈E2，设Ψ(t,u)=P2Φ(t,u)=u-K(t,u)，则由式(28)知Ψ(t,u)≠0,u∈∂Q.于是对任意t∈[0,1]，deg(Ψ(t,·)，Q，0)有定义且

deg(Ψ(t,·)，Q，0)=deg(Ψ(0,·)，Q，0)=deg(id,Q,0)=1

因此存在满足条件的z(t)∈Q，即S和∂Q环绕.

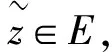
第三步. 我们将证明这个弱解其实也是系统(1)的经典解.

(29)

特别地，若令ζ=e1,e2,…,e2n, 则式(29)表明

由式(8)知

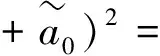
(30)

于是有

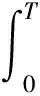
(31)

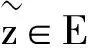
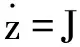
(32)

对式(32)两边分别与Jζ(ζ∈W1/2,2([0,T]，R2n)做内积，并由分部积分可知

(33)

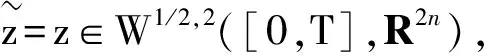
参考文献：

[1] RABINOWITZ PH. Minimax methods in critical point theory with applications to differential equations [M]. RI: CBMS Regional Conf Ser in Math, 1986.

[2] RABINOWITZ P H. Periodic solution of Hamiltonian systems [J]. Comm. Pure Appl. Math., 1978, 31: 157-184.

[3] EKELAND I. Convexity Methods in Hamiltonian Mechanics [M]. New York: Springer-Verlag, 1990.

[4] CHANG K. Critical point theory and its applications (in Chinese) [M]. Shanghai: Science and technology publishing company, 1986.

[5] FRIEDMAN A. Partial differential equations [M]. Dover: Dover Publications Inc., 1969.

[6] RABINOWITZ P H. Periodic solution of Hamiltonian systems: a survey, Math [R]. Research Center Technical Summary Report, University of Wisconsin-Madison.

[7] COPPZI A. On Subquadratic not-autonomous Hamiltonian systems [M]. Berlin: Springer-Verlag, 1983. 122-131.

[8] AMANN H. Saddle points and multiple solutions of differential equations [J]. Math. Z., 1979, 169: 127-166.

[9] AMANN H, ZEHNDER E. Nontrivial solutions for a class of nonresonance problems and applications to nonlinear differential equations [J]. Ann. Sc. Norm. Sup. Pisa, C1. Sci. IV Ser., 1980, 7: 539-603.

[10] CHONG L, CHUNGEN L. The existence of nontrival solutions of Hamiltoian systems with Lagrangian boundary conditions[J]. Acta Mathematica Scientia, 2009, 29 B (2): 313-326.

Existence of periodic solutions of subquadratic Hamiltonian systems

ZHANG Xiao-jing, GUO Fei

(School of science, Tianjin University, Tianjin 300072, China)

In this paper, a result on existence of periodic solutions of subquadratic Hamiltonian systems was proved by the minimax methods.

periodic solutions; Hamiltonian systems; subquadratic conditions; minimax methods; variational principle

2014-04-14.

国家自然科学基金(10901118)；天津大学“北洋学者青年骨干教师计划项目”

张小静(1988-)，女，硕士，研究方向：非线性分析.

郭 飞(1979-)，女，副教授，研究方向：非线性分析.

O175

A

1672-0946(2015)05-0614-06