地铁隧道地震动力响应三维数值分析

宋稳明 陈清波

地铁隧道地震动力响应三维数值分析

宋稳明 陈清波

摘 要：文章依托广州地铁花都广场站—马鞍山公园站区间隧道工程，建立地铁隧道地震动力响应三维数值分析有限元模型，计算分析水平向地震荷载作用下的地表位移、隧道结构动力响应，并计算分析了不同阻尼、边界条件等计算参数对隧道结构动力响应的影响。

关键词：地铁隧道；地震荷载；动力响应；数值分析

宋稳明：广东省南粤交通投资建设有限公司，硕士，广东广州 510100

目前，我国地铁已进入快速发展时期，其安全受到地震等自然灾害的严重威胁。地震发生时，地下结构周围的土体受到地震波的影响会产生较大的变形，地下结构会因地震动力响应过大造成破坏，因此，对地铁隧道结构进行动力响应计算分析具有重要意义。

1　工程概况

广州地铁花都广场站—马鞍山公园站区间隧道最大纵坡6.613‰，最短坡长250 m，最小埋深4.85 m，最大埋深8.6 m。地区场地地形平坦，属广花冲积盆地，上覆饱和砂土分布广泛，有一定厚度，为可液化地层；下伏灰岩分布较稳定，岩溶发育较强烈，分布规律性差，形态规模难以确定，且岩溶发育可导致地面塌陷；场地土的类型属中软土，建筑场地类别为Ⅱ类，场地地基液化等级属轻微液化，为抗震不利地段。

2　地震动力响应三维数值分析

2.1有限元模型的建立

有限元模型建立中假定，地震由地下的基岩处产生加速度，以地震波的方式入射，包括压缩波和剪切波，用材料阻尼来描述系统阻尼，计算中使用总应力法，忽略地震导致的砂土液化以及孔隙水压力的变化。

有限元模型的土体深度取80 m，隧道长200 m。为了使地震波在有限元模型边沿处的反射作用降到最低，模型选用无限元边界条件进行模拟。选用Mohr-Coulomb本构模型作为土体的本构模型，隧道结构为线弹性模型。假定土体和隧道结构接触界面满足位移协调条件，即不发生相对的滑动和脱离。结合该地区岩土分层以及计算需要对模型进行简化，将土体分为3层。隧道结构为圆形，其中外直径取为10 m，衬砌厚度为0.5 m，密度取为2 400 kg/m3，泊松比为0.15，弹性模量取为35 GPa。所建立的三维有限元模型见图1，土体参数见表1。

图1　三维有限元模型

材料的阻尼比均设为0.05，输入的地震波为广州人工波（图2），地震烈度分别按照7、8、9度来考虑。考虑到广州人工波给出的只是剪切波的时程曲线，结合以往的工程经验以及抗震规范，将压缩波的大小按照剪切波大小的2/3缩小，作为水平地震荷载施加。

2.2水平向地震作用下地震动力响应

2.2.1地表水平位移

为考察在水平向地震作用下地表水平位移，分别对无隧道衬砌（自由场）和有隧道衬砌时的地表水平位移进行了计算分析。将有限元模型的纵向方向分为20个部分，分别提取地震作用后的计算结果中各个部分的地表水平位移最大值，图3给出了各个部分的地表最大水平位移值与隧道长度的关系。由图3可知，隧道上部地表水平位移最大值出现在隧道的两端，隧道中部的地表位移值变化不大。通过无隧道衬砌（自由场）的地表水平位移最大值与有隧道衬砌的地表水平位移最大值相比较可以发现，隧道衬砌的存在导致地表水平位移增加，但增加的幅度不大，两者仅仅相差1.4 cm。

2.2.2隧道结构水平位移

水平向地震荷载对隧道结构的破坏非常大，在计算分析水平向地震对隧道结构的动力影响时，需选取地表水平向位移变化最为剧烈的隧道截面。由图3可知，在距离隧道两端20 m左右的范围内，地表水平位移出现急剧变化，对应地表水平最大位移图形出现尖顶，意味着内力的急剧变化。鉴于篇幅的原因，本文选择地震烈度为7度，距离隧道端部20 m的截面作为控制性截面，进行水平向地震荷载作用下隧道结构水平位移计算。

图4为水平向地震荷载作用下，隧道结构的最大水平位移云图。图5为水平向地震荷载作用下，隧道结构顶、底部相对水平位移时程曲线。

由图4可知，隧道结构的水平位移随着地震烈度的提高而增大，当地震烈度为7度的时候，隧道结构的最大水平位移值为2.806 cm，出现在隧道结构的底部；当地震烈度为8度的时候，隧道结构的最大水平位移值为6.583 cm，出现在隧道结构的左下部；当地震烈度为9度的时候，隧道结构的最大水平位移值为10.22 cm，出现在隧道结构的左下部。

表1　土体物理力学参数

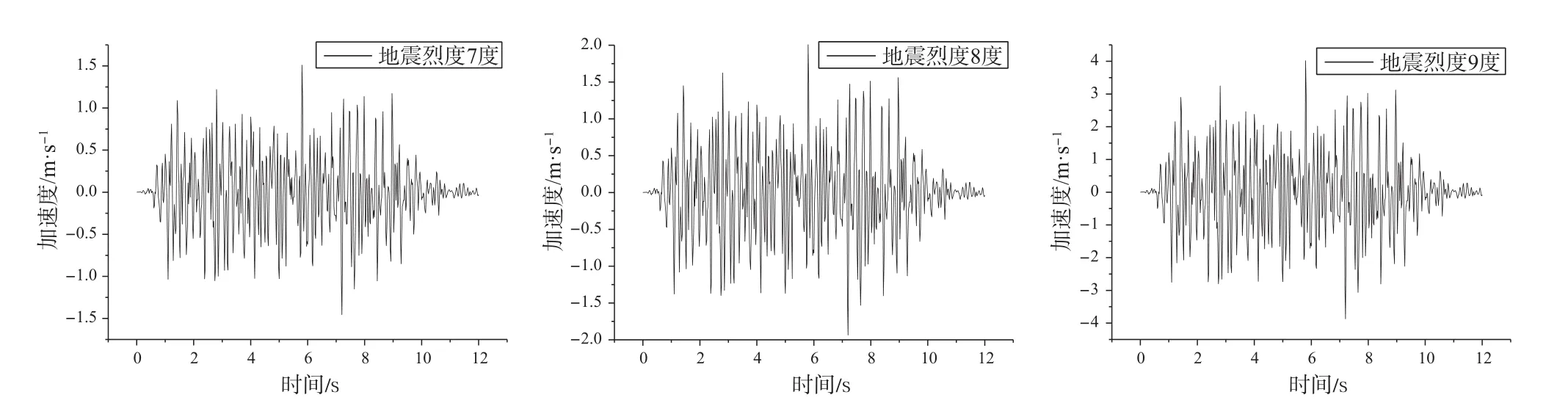
图2　广州人工波加速度时程曲线

图3　地表水平位移最大值分布图

由图5可知，当地震烈度为7度的时候，隧道结构的顶部和底部的相对位移最大值为1.58 cm；当地震烈度为8度的时候，隧道结构的顶部和底部的相对位移最大值为3.79 cm；当地震烈度为9度的时候，隧道结构的顶部和底部的相对位移最大值为5.02 cm。隧道结构的顶部和底部的相对位移最大值出现的时间均在5 s左右。

2.2.3隧道结构应力

图6为隧道结构在受到水平向地震荷载作用下的最大Mises应力云图，可以看出，当地震烈度为7度的时候，隧道结构顶部的Mises应力最大值为116.7 kPa；当地震烈度为8度的时候，隧道结构顶部的Mises应力最大值为403.8 kPa；当地震烈度为9度的时候，隧道结构顶部的Mises应力最大值为855.4 kPa。这表明，隧道结构应力随着地震烈度的提高呈倍数增大。

图4　隧道结构最大水平位移云图（单位：m）

图5　隧道结构顶部和底部相对水平位移时程曲线

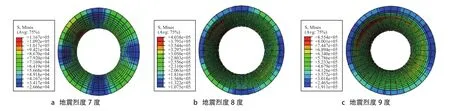
图6　隧道结构最大Mises应力云图（单位：Pa）

3　计算参数对地震动力响应的影响

3.1土体阻尼的影响

为分析水平向地震荷载作用下，不同土体阻尼对隧道结构动力响应的影响，本文选取土体的阻尼比分别为0.05、0.02和0，计算分析土体阻尼比改变后地震对隧道结构的动力响应。计算时，隧道结构的阻尼比设为0.05，并保持其他参数以及边界条件不变，入射地震波选取的是地震烈度为8度的地震加速度。表2给出了不同土体阻尼比情况下隧道结构的最大动力响应，包括水平加速度a、水平位移u、Mises应力、弯矩M和剪力Q。

从表2可以看出，隧道结构的地震响应大小受土体阻尼比的影响很大。从表2中隧道结构的最大水平加速度可以看出，隧道结构最大水平加速度随着土体阻尼比的增大而减小。同时，隧道结构的水平位移、Mises应力、弯矩和剪力也随着土体阻尼比的增大而减小。从这一方面也可以看出，土体阻尼比的取值直接关系到隧道结构动力响应的计算结果。

3.2隧道结构阻尼的影响

为分析水平向地震荷载作用下，不同隧道结构阻尼对隧道结构动力响应的影响，本文选取隧道结构的阻尼比分别为0.1、0.05和0，计算分析隧道结构阻尼比改变后地震对隧道结构的动力响应。计算时，土体的阻尼比设为0.05，并保持其他参数以及边界条件不变，入射地震波选取的是地震烈度为8度的地震加速度。表3给出了不同隧道结构阻尼比情况下隧道结构的最大动力响应，包括水平加速度a、水平位移u、Mises应力、弯矩M和剪力Q。

由表3可知，改变隧道结构结构阻尼比对隧道结构的动力响应影响不大，阻尼比为0时，隧道结构的最大水平加速度仅仅比阻尼比为0.1时的最大水平加速度增大了0.000 1 m/s2（0.01%），同样，对隧道结构的水平位移和剪力也影响不大，而对隧道结构的Mises应力和弯矩影响较大，分别增大了0.1207 MPa和3.02 kN·m（34%和9%）。3.3 边界条件的影响

为分析有限元模型不同边界条件对隧道结构动力响应的影响，本文选取了固定边界、无限元以及自由边界3种边界条件进行地震对隧道结构动力响应影响的计算，计算中入射地震波选取地震烈度为8度时的地震加速度。表4给出了不同边界条件下隧道结构的最大动力响应，包括水平加速度a、水平位移u、Mises应力、弯矩M和剪力Q。

由表4可见，不同边界条件的设定对于隧道结构动力响应的影响比较大。固定边界条件下，计算得到的隧道结构剪力Q、弯矩M、Mises应力、水平位移u和水平加速度a相比无限元边界条件下计算得到的结果要小，而自由边界条件下的计算结果相比无限元边界条件下的计算结果要大。由此表明，利用固定边界条件下的隧道动力响应计算结果进行抗震设计将会导致设计偏于危险，而利用自由边界条件下的隧道动力响应计算结果进行抗震设计将会导致设计偏于保守。

表2　不同土体阻尼时隧道结构动力响应

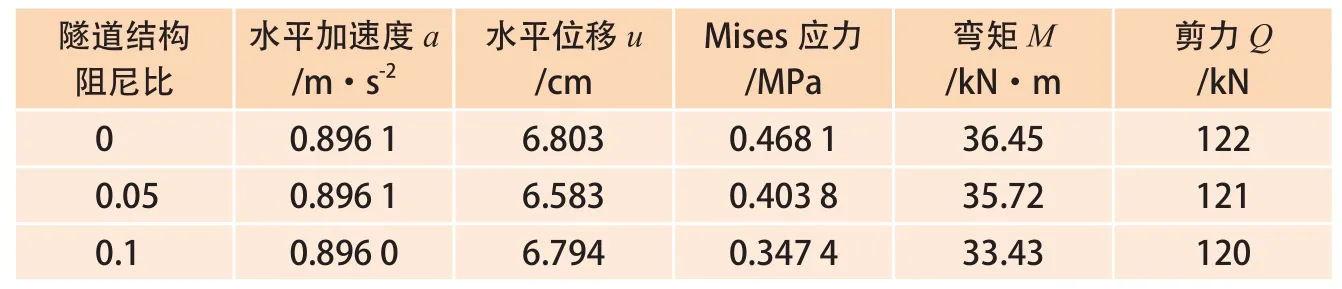
表3　不同隧道结构阻尼时隧道结构动力响应

表4　不同边界条件时隧道结构动力响应

参考文献

[1] 吴波. 城市地下工程技术研究与实践[M]. 北京：中国铁道出版社，2008.

[2] 侯公羽，刘宏伟，李晶晶. 基于开挖卸荷效应的地铁隧道施工过程数值分析[J]. 岩石力学与工程学，2013，32（增1）.

[3] 陈代秉. 地铁盾构区间隧道抗震分析[J]. 现代城市轨道交通，2014（2）.

[4] 赵伯明，苏彦. 盾构隧道的纵向地震响应[J]. 中国铁道科学，2009，30（5）.

[5] 焦建林. 土-结构相互作用时地下车站自振频率分析[J]. 现代城市轨道交通，2013（5）.

责任编辑 朱开明

3D Numerical Analysis of Seismic Response of Metro Tunnel

Song Wenming, Chen Qingbo

Abstract:Based on the metro tunnel works of section between Huadu Square station – Ma’anshan Park station of Guangzhou metro, the paper establishes a finite element model of 3D numerical analysis on seismic response, and it calculates and makes analysis of the surface displacement and tunnel structure dynamic response under lateral seismic loads, and analyzes the infl uence of different damping, boundary conditions and calculation parameters on the dynamic response of tunnel structures.

Keywords:metro tunnel, seismic load, dynamic response, numerical analysis

收稿日期2014-11-07

中图分类号：U452.2+8