近地快速交会调相策略设计与任务分析*

杨 震，罗亚中，张 进

(国防科技大学航天科学与工程学院，湖南长沙410073)

从20世纪60年代至今，人类已经进行了几百次交会对接活动［1］。我国于2011年、2012年和2013年分别实现了神舟八号、神舟九号、神舟十号飞船与天宫一号目标航天器的自动和手控交会对接试验，成为继美国、苏联(俄罗斯)之后，第三个独立掌握近地轨道交会对接技术的国家［2］。

从任务持续时间来看，交会对接策略主要经历了三个发展阶段［3］:第一阶段，直接交会对接策略。该策略在1圈内完成交会对接，追踪航天器入轨后直接与目标航天器建立相对导航，相位差很小(约为0.4°)，主要应用于20世纪60年代苏联和美国的交会对接任务中，包括东方－3与东方－4飞船(1962)［4］、阿金纳火箭上面级与双子星－11飞船(1966)［5］等。第二阶段，1天交会对接策略。该策略在一天内完成交会对接，追踪航天器入轨后需要在地面站(船)的测控支持下将其导引至相对导航设备可达范围(距离目标航天器几十公里)，相位角可调节范围为90°±15°，主要应用于20世纪70年代和80年代苏联联盟飞船与礼炮空间站的交会对接任务［6］。第三阶段，2～3天交会对接策略。该策略可将交会对接相位角可调节范围由1天交会策略的30°拓展到180°，避免了目标航天器调相，同时增强了应对多种故障(如飞船推迟发射等)的鲁棒性与安全性。该策略从20世纪90年代沿用至今，是目前地面向国际空间站运送航天员的主要方式，包括联盟飞船、航天飞机与国际空间站［7］及神舟飞船与天宫一号目标航天器［4］的交会对接任务。近期俄罗斯学者对“联盟/进步”飞船与国际空间站的快速交会对接方案进行了设计［7－9］，并从2012年8月到2014年4月，分别采用进步号货运飞船(4次飞行)和联盟号载人飞船(3次飞行)与国际空间站成功实施了7次快速交会对接试验，飞船从入轨到对接仅仅需要6小时。

交会对接过程一般分为远距离导引段(又称为调相段)、近距离导引段、平移靠拢和对接段。调相段变轨的目的是利用低轨道运动速度快的特性，减少两个航天器的相位角差，同时消除追踪航天器入轨时的轨道面偏差。调相变轨策略的选择影响重大，其终端控制精度直接关系到后续阶段任务的成败［1］。随着在轨补给、深空采样返回、空间紧急救援等新的任务需要，一般交会对接技术向长时间和快速(短时间)两个方向拓展。Zhang等［10］对近地多星补给长时间交会任务进行了设计，Labourdette，Baranov［11］和Yang［12］等对火星采样返回任务中的环火星长时间交会问题进行了研究。Murtazin和Budylow［7］对“联盟/进步”飞船与国际空间站快速交会对接的可行性与实施方案进行了研究;Murtazin和Petrov对该快速交会对接方案的任务特性与应急策略进行了分析［8］，并基于进步飞船与国际空间站快速交会对接试验的先验飞行数据，对联盟飞船与国际空间站的快速交会对接方案进行了设计，进一步缩短了交会对接时间［9］。

实施快速交会对接可以减小航天员在狭小飞船空间中生活的压力，减少船载环控生保资源消耗以增大飞船有效载荷运载量，还可以对在轨航天器故障实施快速抢修与紧急救援。由于调相段飞行时间占交会总飞行时间的大部分，快速交会对接主要通过缩短调相段时间来实现，因而飞行时间将缩短，追踪航天器的初始相位角、测控条件、调相段终端控制精度、变轨策略、发射窗口和目标航天器轨道控制策略等相对于现有2天交会对接方案将有较大差异，需要根据具体技术条件进行设计分析。

1 快速交会调相策略设计

1.1 变轨方案设计

远距离导引段的主要控制过程是通过变轨逐步抬升并圆化追踪航天器轨道，同时修正追踪航天器入轨时与目标航天器的初始轨道面偏差，最后使追踪航天器达到终端瞄准点。图1给出了我国交会对接任务中远距离导引段的基本飞行方案［2，13］。

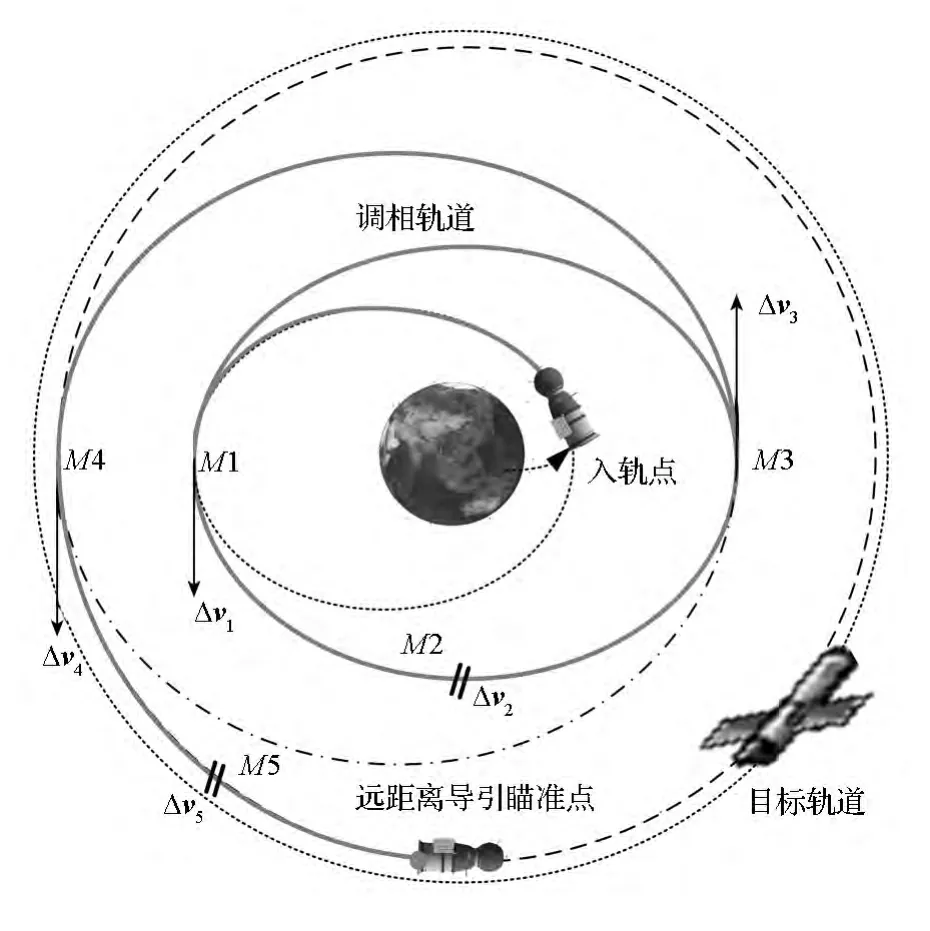
图1 远距离导引段飞行方案示意图Fig.1 Flight profile of long distance rendezvous-phasing mission

如图1所示，追踪航天器发射入轨后，初始轨道为低于目标器轨道的椭圆轨道，需要进行5次变轨以到达瞄准点，分别为:

M1—第N1圈远地点施加迹向冲量Δv1y，抬高近地点高度，进入调相轨道以调整相位角;

M2—第N2圈纬度幅角u2∈［90°，270°］处施加法向冲量Δv2z，同时修正轨道倾角和升交点赤经偏差，调整轨道面;

M3—第N3圈近地点施加迹向冲量Δv3y，抬高远地点高度，调整半长轴;

M4—第N4圈远地点附近u4∈［u4L，u4U］处施加迹向冲量Δv4y，调整偏心率以圆化轨道;

M5—第N5圈纬度幅角u5∈［u5L，u5U］处施加冲量Δv5=［Δv5x，Δv5y，Δv5z］T进行组合轨道修正，该次机动为小量，标称轨道中为零。

在我国2天交会对接任务中［2，13］，5次变轨圈次分别为N1=5，N2=13，N3=16，N4=19，N5=24。其中，每2次变轨间隔的飞行圈数主要用于变轨前后的轨道测定(每次测定需要三圈以上弧段)、变轨参数计算及指令上传。若不考虑测定及第5次组合轨道修正，执行远距离导引变轨机动仅需要2.5圈，如图1中实线段所示:从入轨点(为近地点)起算，追踪航天器飞行0.5圈后执行第一次机动，0.5～1.5圈后在合适轨道位置执行第二次机动，飞行2圈后执行第三次机动，2.5圈执行第四次机动。因此，在追踪航天器精确入轨且不存在控制误差的标称情况下，远距离导引段飞行时间最大可以缩短到2.5圈。

如果远距离导引段飞行时间缩短，则轨道误差短时间内传播较小，可采用入轨点到第一次机动前的N1圈定轨数据计算4次调相机动的变轨参数，采用关联轨道机动以取消后续变轨前后的轨道测定，并取消第五次组合轨道修正。这样远距离导引段飞行时间可减少为N1+2.5圈，以实现快速交会。本文研究基于以下假设:

1)初始轨道参数及近距离交会飞行方案与2天交会任务相同，即目标航天器为平均高度340 km的2天回归轨道，轨道倾角为42.8°，追踪航天器入轨近/远地点高度为200/330 km，远距离导引终端瞄准目标器后下方约52 km;

2)入轨点到第一次机动间隔0.5～1.5圈，若地面站(船)在该测量弧段的定轨精度不能满足远距离导引段终端控制精度要求，则追踪航天器需要基于卫星导航(如北斗二代，全球定位系统等)并具备星上自主规划的能力;

3)追踪航天器具备在1圈内执行两次以上机动的自主控制能力。

在我国2天交会对接任务中，调相段飞行28圈，近距离导引段飞行约1.5圈，若近距离导引飞行方案不变，对N圈快速交会对接，调相段飞行圈数约为N－1.5;若设置入轨点与第一次机动(测定轨弧段)间隔1.5圈，则调相段至少需要3.5圈，总飞行圈数约为5圈。综合上文分析，本文将5圈快速交会对接的调相段变轨方案设计如表1所示。

表1 五圈快速交会调相变轨方案Tab.1 Maneuver plan of five-obit short rendezvous

1.2 变轨任务规划模型

1)设计变量。由表1可知，第1，3次机动位置和第4次机动圈次、机动方向均固定，因此设计变量为第2，4次变轨的机动位置和各次冲量大小，即

2)约束条件。调相终端时刻要求追踪航天器与目标航天器的相对位置、速度一定，该条件一般可由地面导引获得的精度与相对测量传感器的性能等共同确定。

3)求解策略。由式(1)及式(2)可知，6个方程对应6个未知数，存在唯一解。本文采用张进［14］提出的修正特殊点变轨策略，基于近圆偏差方程的非线性解，通过简单迭代来计算摄动条件下精确满足终端条件的变轨参数。

2 任务参数分析

2.1 问题配置

设定初始时刻目标航天器与追踪航天器的轨道根数E=［a，e，i，Ω，ω，υ］(a为半长轴、e为偏心率、i为轨道倾角、Ω为升交点赤经、ω为近地点幅角、υ为真近点角)分别为［2，13］:Et=［6716.3 km，0.000 6，42.85°，50.75°，152.49°，0°］，Ec=［6636 km，0.009，42.84°，50.92°，125.49°，0°］。对5圈快速交会任务，调相段飞行3.5圈约为19 400 s。

高精度轨道预报模型考虑大气阻力和地球非球形引力摄动，大气模型为NRLMSISE 2000，地球引力模型为JGM3(20×20)，大气阻力系数cd=2.2，太阳辐射通量F10.7=150，地磁指数KP=3。在目标航天器当地轨道坐标系(原点o在目标航天器质心，ox轴沿其地心矢径方向，oz轴沿其轨道面法向，oy轴与ox，oz轴构成右手系)中表示的终端瞄准相对运动状态为:

x=－13.5 km，y=－50 km，z=0，vx=0，vy=23.23 m/s，vz=0;

容许误差标准差为:

σx=1.9 km，σy=6.4 km，σz=0.72 km，σvx=4.6 m/s，σvy=0.8 m/s，σvz=0.7 m/s。

2.2 测控条件分析

当初始相位角为20°，调相段飞行时间为19 400s时，采用表1所示的变轨方案和2.2节所述的规划模型，求解得追踪航天器调相段标称变轨参数如表2所示，对应追踪航天器调相段星下点轨迹如图2所示。

表2 四脉冲调相变轨方案Tab.2 Four-impulse phasing maneuver plan

图2 追踪航天器星下点轨迹图Fig.2 Subsatellite point trajectory of chasing spacecraft

由图2可知，中继星1，2，3可覆盖追踪航天器大部分飞行弧段，从追踪航天器入轨到第1次机动，依次可被主场、渭南、青岛、厦门、“远望五号”测量船、“远望六号”测量船、智利、阿尔卡特拉、喀什、和田等测站测控。第1次机动后可被智利站测控，第2次机动可被中继星1，3测控，第3次机动可被中继星1，3及卡拉奇站测控，第4次机动可被中继星2测控。因此，若仅依靠地面测控站(船)，则第2，4次机动不可测控，需要追踪航天器进行自主控制。

实际任务中，由于动力学模型偏差、导航偏差和控制偏差等因素影响，航天器真实轨道会偏离设计轨道。本文通过Monte Carlo打靶仿真［15］，分析为达到调相段终端控制精度要求所需要的初始定轨精度。

假设模型误差、导航误差、控制误差均满足高斯分布，对近地交会轨道，大气阻力摄动是最大的不确定性因素，主要是大气密度存在误差，由于大气密度在轨道上不断变化，很难直接评估，本文采用在阻力系数cd上施加误差的方法来分析大气阻力误差的影响，目标航天器和追踪航天器的模型误差标准差均取为σcd=0.05，在J2000地心惯性系下表示的导航误差标准差均取为σrv=［10fm，10fm，10fm，0.005fm/s，0.005fm/s，0.005fm/s］，其中f为待定系数。追踪航天器变轨脉冲矢量大小误差标准差为σΔv=0.01+0.000 5×Δv(m/s)，变轨脉冲矢量俯仰角、偏航角误差标准差分别为σp=0.5°，σy=0.5°，Monte Carlo打靶样本点数为1000。

仿真表明，相同的定轨精度下，横向相对位置偏差(y)散播最快，最容易超出调相段终端控制精度要求范围，本文通过数据拟合来确定横向相对位置偏差随定轨误差中系数f的变化关系。如图3所示，首先给定几个不同的f值，通过打靶计算出对应的终端横向相对位置误差标准差;然后采用二阶曲线拟合，求解出二者函数关系为:f=最后根据终端横向位置精度指标要求求值σδy=6.4 km，求解出:f≈4。则可计算出满足终端控制精度要求的初始定轨误差标准差不能大于:σrv=［40 m，40 m，40 m，0.02 m/s，0.02 m/s，0.02 m/s］，此时计算得到的终端相对状态均值为:

x=－13 566.9m，y=－50 207.9m，z=－1.8m，vx=0.019 m/s，vy=23.38 m/s，vz=0.002 m/s;

标准差为:

σx=131.2 m，σy=6369.2 m，σz=39.0 m，σvx=0.34 m/s，σvy=0.32 m/s，σvz=0.28 m/s。

可知当初始定轨位置误差为70 m，速度误差为0.035 m/s时，能满足5圈快速交会调相段终端控制精度要求。因此，若地面测控站(船)在追踪器入轨后1.5圈内的定轨精度大于该值，则需要采用天基导航或者增加调相机动前的飞行圈数。若1.5圈内地面站不能完成变轨参数计算及指令上传，则需要追踪航天器进行自主规划。

图3 定轨误差系数与终端控制精度关系曲线Fig.3 Relation curve of orbit determination error coefficient and terminal control accuracy

2.3 总速度增量及初始相位角分析

在调相段，相同的约束条件下，初始相位角的大小影响调相轨道的高度和总速度增量的大小。对于典型的共面且初始轨道不相交的交会情况，存在燃料消耗最小的最优初始相位角区域。当初始相位角处于该区域内时，所有交会脉冲同向(均为制动或加速);处于该区域外时，交会脉冲不同向(制动与加速并存)，使总速度增量增大，增大量与最优区域边界的距离近似呈线性关系增加［16］。

2.3.1 追踪航天器入轨周期误差影响分析

设置调相段飞行时间3.5圈，目标轨道高度340 km。当追踪航天器入轨轨道周期误差标准差分别为σT=5 s和σT=10 s时，总速度增量随初始相位角变化关系的300次Monte Carlo打靶仿真结果如图4所示。可知当σT=10 s时，最优相位角范围约为8°，总速度增量均值约为54 m/s，当σT=5 s时，最优相位角范围约为10°，总速度增量均值约为52 m/s，即入轨轨道周期精度提高1倍使得最优相位角范围增大了2°。因此提高追踪航天器入轨精度可以增大快速调相交会的最优初始相位角范围，同时减少燃料消耗。

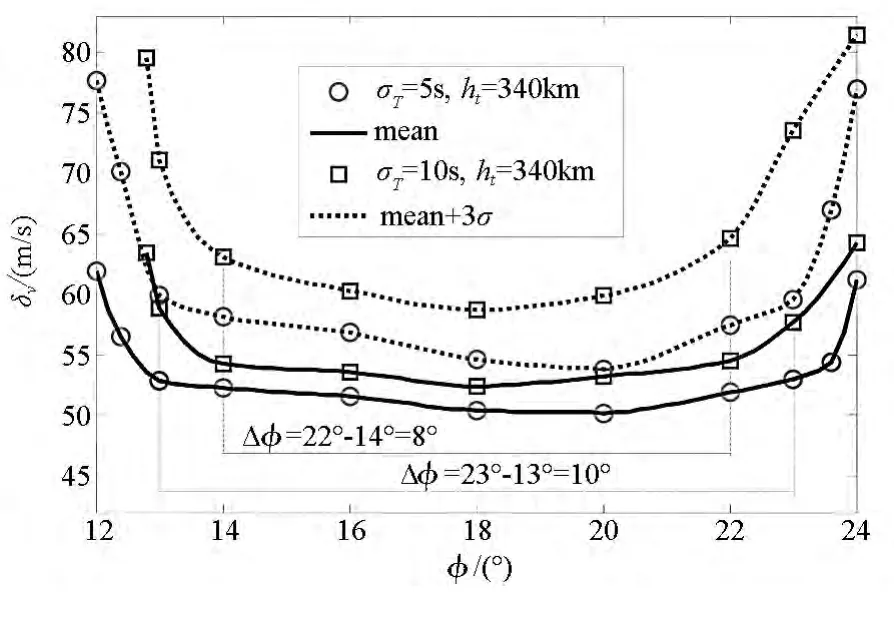
图4 追踪器不同入轨周期误差下的最优相位角范围Fig.4 Optimal phase angle range in different chaser’s inserting orbital period error

2.3.2 目标轨道高度影响分析

设置调相段飞行时间为3.5圈，追踪航天器入轨轨道周期误差标准差σT=5 s。当目标轨道高度分别为340 km和370 km时，总速度增量随初始相位角变化关系的300次Monte Carlo打靶仿真结果如图5所示。可知当ht=340 km时，最优相位角范围约为10°，总速度增量约为52 m/s;当ht=370 km时，最优相位角范围约为12°，总速度增量约为68 m/s，即追踪航天器入轨精度一定时，目标轨道高度越高，最优相位角范围越大，总速度增量也越大，且随着目标轨道高度增加，最优相位角的上、下边界值右移增大。

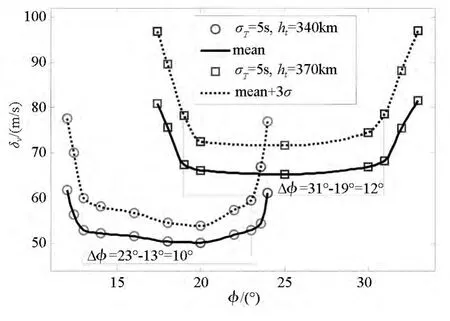
图5 不同目标轨道高度下的最优相位角范围Fig.5 Optimal phase range in different target orbit height

2.3.3 追踪航天器入轨远地点高度影响分析

在调相段飞行时间为3.5圈，目标轨道高度为340 km的标称状态下(不考虑任何偏差因素)，当追踪航天器入轨远地点高度分别为250 km，290 km和330 km时，总速度增量随初始相位角变化关系如图6所示。可知追踪航天器入轨远地点高度越高(仍小于目标轨道高度)，则最优相位角范围越大，总速度增量越小，且随着入轨远地点高度增加，最优初始相位角的上、下边界左移减小。

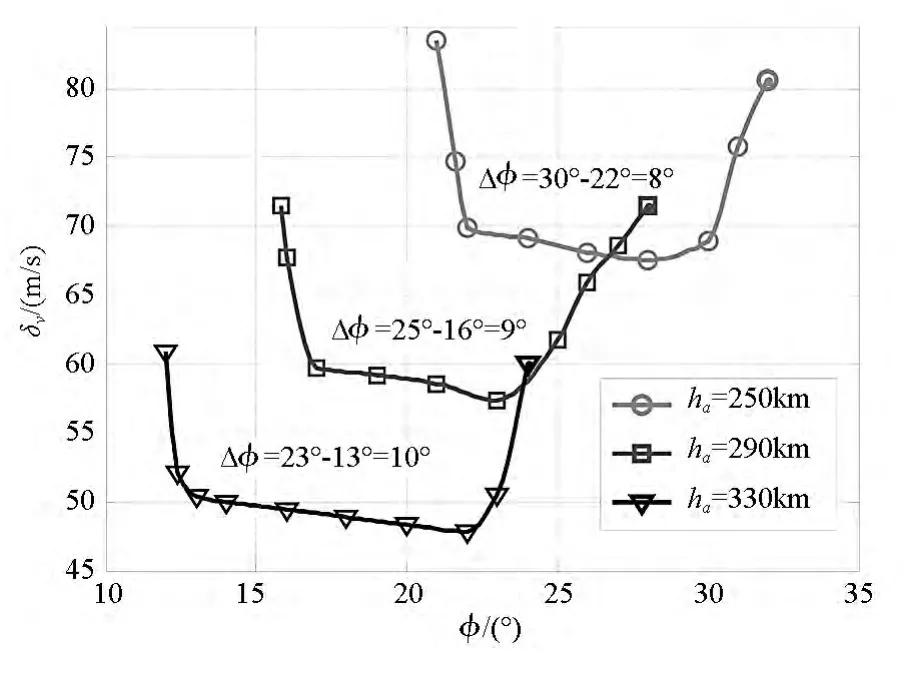
图6 追踪器不同入轨远地点高度下的最优相位角范围Fig.6 Optimal phase range in different orbit apogee height of chaser

2.3.4 终端瞄准点影响分析

设置调相段飞行时间为3.5圈，目标轨道高度为340 km。当调相段终端瞄准点由2天交会任务的52 km改为5 km停泊点(相对状态为:x=0，y=－5 km，z=0，vx=0，vy=0，vz=0)时，总速度增量随初始相位角变化关系如图7所示。可知终端瞄准点为52 km时，最优初始相位角范围约为10°，总速度增量约为49 m/s;终端瞄准点为5 km时，最优初始相位角范围约为16°，总速度增量约为56 m/s，即最优初始相位角范围增大了约6°。这是因为在交会总时间不变的情况下，若调相段直接瞄准5 km停泊点，则2天交会中寻的段的飞行时间(约70 min)可用于调相，增加了调相时间，使得最优初始相位角范围的上限增大，而增加的7 m/s的速度增量是2天交会中寻的段所需的速度增量。因此在控制精度允许的情况下，调相段直接瞄准5 km停泊点可增大最优初始相位角范围，而不改变总速度增量。

图7 不同终端瞄准点下的最优相位角范围Fig.7 Optimal phase range in different aiming points

2.3.5 调相时间影响分析

图8给出了5圈快速交会和现有2天交会调相段总速度增量与初始相位角变化关系。

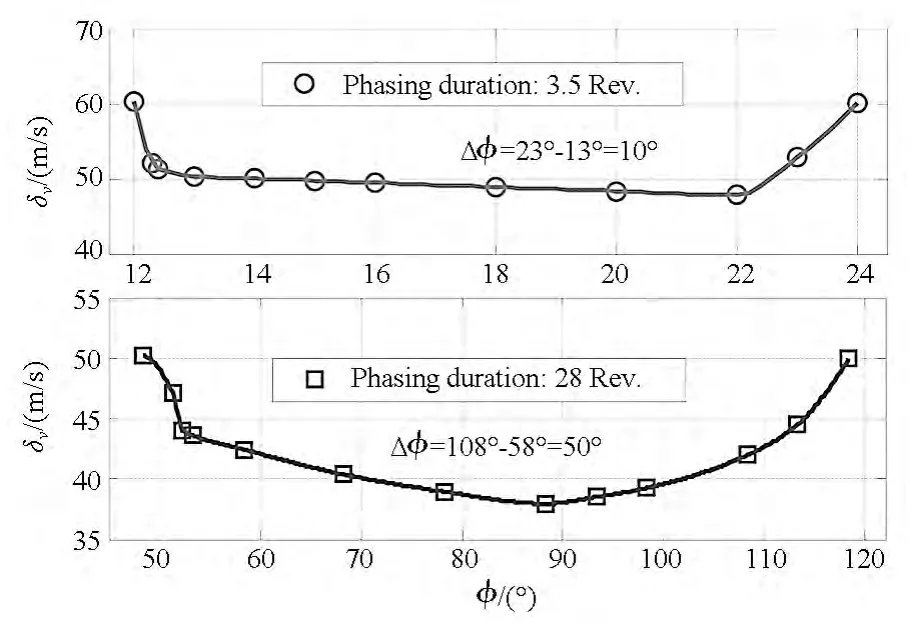
图8 3.5圈与28圈快速调相交会对比Fig.8 Comparison of 3.5 revolutions with 28 revolutions

可知5圈快速交会的最优初始相位角范围为10°，总速度增量约为49 m/s，2天交会最优初始相位角范围为50°，总速度增量约为39 m/s。因为5圈快速交会的初始轨道参数直接采用了2天交会任务的轨道参数，所以第二次调整轨道面偏差(主要是赤经偏差)的机动比2天交会的多约10 m/s。由于调相时间短，追踪轨道与目标轨道升交点赤经在地球引力J2项摄动下相对漂移小，5圈交会发射应该比2天交会稍微滞后以预留更小的初始赤经偏差。因此，当初始相位角范围在最优相位角区域内时，初始相位角基本不影响调相所需的总速度增量。

图9进一步给出了调相时间分别为3.5圈(19 400 s)、4.5圈(24 400 s)、5.5圈(29 800 s)、6.5圈(35 300 s)、7.5圈(40 800 s)时，最优初始相位角范围随调相段飞行圈数的变化关系，可知最优初始相位角范围随调相时间增加而近似线性增大(10°～28°)。

图9 不同调相时间下的最优相位角范围Fig.9 Optimal phase range in different phasing duration

2.4 目标调相与发射机会分析

根据轨道动力学原理，轨道平均角速率偏差与轨道半长轴偏差及切向机动与轨道半长轴偏差的关系可分别表示为［1］

其中，a为目标轨道半长轴，n为其平均轨道角速率，δvt为切向冲量δv t大小。

可得相位调整量与切向机动的关系为

由式(4)可得，对2天回归轨道(轨道高度约为347 km)，施加δv t的切向冲量，N天之中可使目标轨道相位角调整Δφ≈N×2.208×δvt(°)。在现有2天交会对接方案中，追踪航天器入轨时刻与目标航天器之间的相位角约为88°，若5圈快速交会的初始相位角设计为18°，则相对2天交会对接方案目标航天器需要多调整的相位角为70°。为了满足快速交会的初始相位角，若不改变2天调相交会任务的目标航天器调相变轨时刻(N不变)，则调整该相位角需要约为δvt≈31.70/N(m/s)的速度增量;若不改变2天调相交会任务的目标航天器调相变轨冲量(δv t不变)，则需要比2天任务提前N≈31.70/δvt(d)进行目标轨道调相机动。

由于目标航天器实际轨道高度与设计轨道高度(2天回归轨道约为347 km，3天回归轨道约为398 km)存在偏差δa(km)，将引起初始相位角漂移，由式(3)可知，对2天回归轨道，每天漂移的相位角大小为Δφ≈δa×1.264(°/d)。若实际轨道与2天回归轨道高度偏差5km，则在一个回归周期(2天)内相位角漂移12.6°;因为5圈快速调相交会的最优相位角范围约为10°，则第二个回归周期(2天后)快速调相交会的初始相位条件将不能满足，即追踪航天器只有一次发射机会。

3 结论

基于我国现有2天交会对接方案，对实施5圈快速交会对接的变轨方案与规划模型进行了研究。仿真结果表明，实施快速交会对接任务，需要追踪航天器具备自主控制的能力，且需要的定轨位置精度为70 m、速度精度为0.035 m/s。对目标轨道高度340 km，追踪航天器入轨近/远地点高度200/330 km，调相终端瞄准目标航天器后下方52 km的5圈快速交会对接任务，其最优相位角范围约为10°(13°～23°)。

References)

［1］唐国金，罗亚中，张进.空间交会对接任务规划［M］.北京:科学出版社，2008.TANG Guojin，LUO Yazhong，ZHANG Jin.Mission planning of space rendezvous and docking［M］.Beijing:Science Press，2008.(in Chinese)

［2］周建平.天宫一号/神舟八号交会对接任务总体评述［J］.载人航天，2012，18(1):1－5.ZHOU Jianping.A review of tiangong－1/shenzhou－8 rendezvous and docking mission［J］.Manned Spaceflight，2012，18(1):1－5.(in Chinese)

［3］杨震.自主交会调相任务优化策略与相对轨迹预报算法［D］.长沙:国防科学技术大学，2013.YANG Zhen.Phasing mission optimization approaches and relative orbit propagation algorithms for autonomous rendezvous［D］.Changsha:National University of Defense Technology，2013.(in Chinese)

［4］Branetc V N.To 40－aniversary of first automatic docking in space［R］.Universe，Infinity，Time，11，Kiev，2007.

［5］Lunney G S.Summary of gemini rendezvous experience［J］.AIAA Flight Test，Simulation and Support Conference，AIAA Paper 67－272.

［6］Fehse W.Automated rendezvous and docking of spacecraft［M］.London:Cambridge University Press，2003.

［7］Murtazin R F，Budylov S G.Short rendezvous missions for advanced Russian human spacecraft［J］.Acta Astronautica，2010，67(7－8):900－909.

［8］Murtazin R F，Petrov N.Short profile for the human spacecraft soyuz-TMA rendezvous mission to the ISS［J］.Acta Astronautica，2012，77:77－82.

［9］Murtazin R F，Petrov N.Usage of pre-flight data in short rendezvous mission of soyuz-TMA spacecrafts［J］.Acta Astronautica，2014，93:71－76.

［10］Zhang J，Luo Y Z，Tang G J.Hybrid planning for LEO longduration multi-spacecraft rendezvous mission［J］.SCIENCE CHINA Technological Sciences，2012，55(1):233－243.

［11］Labourdette P，Baranov A A.Strategies for on-orbit rendezvous circling mars［J］.Advances in the Astronautic Science，2002，109:1351－1368.

［12］Yang Z，Luo Y Z，Zhang J.Two-level optimization approach for mars orbital long-duration，large non-coplanar rendezvous phasing maneuvers［J］.Advances in Space Research，2013，52:883－894.

［13］李革非，宋军，刘成军.交会对接任务轨道控制规划设计与实施［J］.载人航天，2014，20(1):2－8.LI Gefei，SONG Jun，LIU Chengjun.Design and implementation of orbit maneuver programming in rendezvous and docking missions［J］.Manned Spaceflight，2014，20(1):2－8.(in Chinese)

［14］张进.空间交会远程导引变轨任务规划［D］.长沙:国防科学技术大学，2008.ZHANG Jin.Mission planning of space rendezvous phasing maneuvers［D］.Changsha:National University of Defense Technology，2008.(in Chinese)

［15］李革非，陈莉丹.交会对接地面导引精度分析研究［C］.第一届全国载人航天飞行动力学技术研讨会，海南，三亚，2012，357－363.LI Gefei，CHEN Lidan.Precision analysis of ground navigation of rendezvous［C］.Proceedings of 1st National Manned Space Congress，Sanya，Hainan，2012，357－363.(in Chinese)

［16］郭海林，曲广吉.航天器空间交会过程综合变轨策略研究［J］.中国空间科学技术，2004，3:60－67.GUO Hailin，QU Guangji.Study on synthetic orbit maneuver of spacecraft during space rendezvous［J］.Chinese Space Science and Technology，2004，3:60－67.(in Chinese)