碟形橡胶准零刚度隔振器的设计和特性分析*

徐道临, 周 杰,周加喜,张 敬

(湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082)

碟形橡胶准零刚度隔振器的设计和特性分析*

徐道临†, 周 杰,周加喜,张 敬

(湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082)

设计了具有准零刚度(QZS)特性的碟形橡胶隔振器，并分析了其隔振特性.隔振器由负刚度元件碟形橡胶(内含钢材料的筋)与正刚度元件竖直橡胶柱并联组装而成.基于Abaqus有限元仿真分析，给出了隔振器在静平衡位置处出现零刚度时，碟形橡胶元件和竖直橡胶元件分别需要满足的构型和尺寸参数条件，得到了隔振器的回复力曲线，并用仅含三次的多项式进行了拟合.进一步，建立隔振系统动力学方程，基于谐波平衡法分析了系统的隔振特性，并与Abaqus动力学仿真分析进行对比，结果表明，碟形橡胶准零系统隔振性能明显优于相应的线性系统.

准零刚度；碟形橡胶；隔振器；低频隔振

准零刚度的实现一般是通过正刚度和负刚度的并联，其典型的设计形式是用线性的竖直弹簧和两根斜弹簧并联来实现[1,2,3].其他方法有：利用空气弹簧实现准零刚度[4]；利用受轴压的梁和正刚度弹簧组合[5]；利用具有软弹簧特性的高度变形的挤压环[6,7];利用磁铁或电磁铁提供负刚度[8,9]；采用6根杆与1根拉簧组合[10]；利用凸轮-滚轮-弹簧机构提供负刚度[11]；Zhou[12]通过磁铁弹簧与机械弹簧并联实现了高静刚度低动刚度，并通过实验验证了其隔振效果.

上述空气弹簧与电磁铁准零刚度隔振器方案等存在体积大，难以实现工程化等缺点，而其他的像凸轮-滚轮-弹簧机构也是原理性的验证，在紧凑性上有所缺陷.本文提出可实现紧凑化设计的碟形橡胶准零刚度隔振器.首先，给出碟形橡胶准零刚度隔振器的设计方案，利用Abaqus仿真分析给出碟形橡胶元件的负刚度曲线及竖直橡胶元件的正刚度曲线，并调整正负刚度元件设计参数，使碟形元件压至水平时的负刚度值与竖直橡胶元件刚度相等，以满足零刚度条件，进而将正负刚度元件并联组装形成准零刚度隔振器，并给出其回复力曲线；其次，用仅含三次方的多项式对回复力进行拟合，得到近似解析表达式，并利用谐波平衡法给出力传递率近似解析表达式；最后，利用有限元动力学分析，评估系统隔振性能，并与线性系统对比，验证碟形准零刚度隔振系统的优越性.

1 碟形橡胶准零刚度隔振器设计

准零刚度特性一般是通过把负刚度单元和正刚度单元并联组合起来实现.本文的准零刚度隔振器是由产生负刚度的碟形橡胶(3)和提供正刚度的竖直橡胶块(4)并联组合而成的，如图1所示.

系统隔振机理是：被隔振物通过(6)承载接头与隔振器连接，碟形橡胶(3)被压至水平位置(即系统的静平衡位置)，此时蝶形橡胶提供负刚度与竖直橡胶块(6)的正刚度并联抵消而成为零刚度,系统在平衡位置附近振动时，固有频率低，可实现低频隔振.

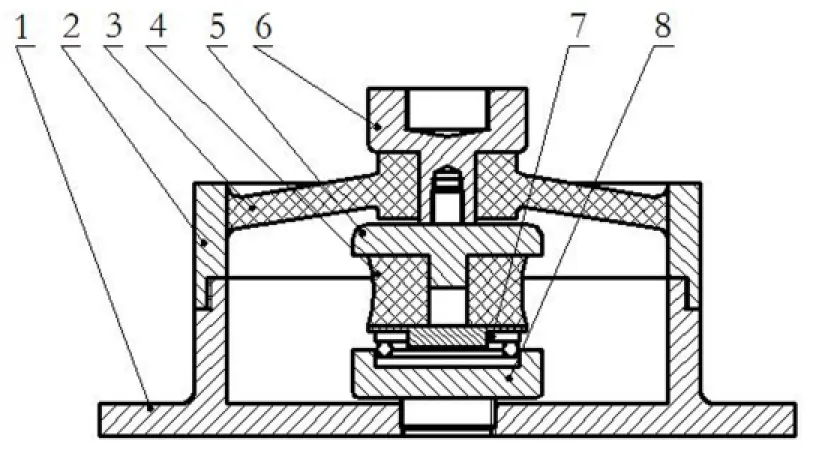
(a)加载前

(b)加载后

2 碟形橡胶的设计和刚度分析

碟形橡胶是该QZS隔振器设计中的重要组成部分， 首先借鉴碟形弹簧的分析理论进行设计，再利用Abaqus仿真分析设计碟形弹簧的构型和参数.图2为碟形橡胶的结构示意图，为达到提高刚度的效果，碟形橡胶里面加有钢筋材料.图中f为加载的力，x为碟形橡胶的变形量，t为碟形橡胶的斜面厚度，h0为碟形橡胶的斜面高度，D为碟形橡胶被压平时的直径.

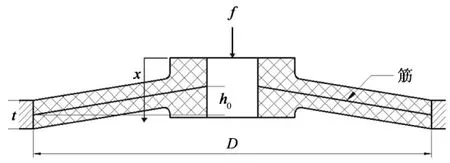
图2 碟形橡胶示意图

2.1 碟形弹簧的理论计算

根据弹性力学理论[13]，碟形弹簧的轴向载荷f与位移变形量x的关系是：

(1)

式中：f为轴向载荷，N;t为弹簧厚度，mm；D为碟形弹簧的外径，mm；x为碟形弹簧的变形量，mm；h0为碟形弹簧压平时的变形量的计算值，mm；E为弹性模量，MPa；μ为泊松比；K1,K4为计算系数．

此处为无支撑面型，所以取K4=1,式(1)对位移求导得：

(2)

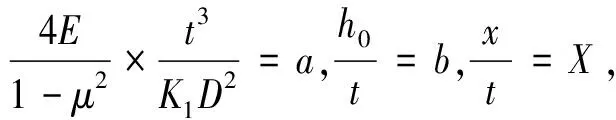
k=a(1.5X2-3bX+b2+1)．

(3)

2.2 碟形橡胶的有限元分析

考虑承载质量m=11kg，隔振频率低于4Hz.以上述理论分析为指导，初步设计了结构参数h0=4 mm,D=140 mm，橡胶厚度t=10 mm.沿碟形橡胶面一周均布50根径向筋，其横截面半径为r=0.6 mm.

由于设计中必须考虑上盖(2)与碟形橡胶(3)硫化固结的圆滑过渡工艺要求，这会影响碟形橡胶刚度；另外加筋碟形橡胶的理论刚度很难确定，需要采用有限元分析获得.图3为碟形橡胶在受力状态下的三维有限元模型，由于本模型具有轴对称性，所以选择一半的模型作为分析对象.橡胶部分的单元类型为C3D8RH，刚体部分为C3D8R, 筋单元为B31.由于本模型在平衡位置附近会呈现负刚度特性，故加力载荷在水平平衡位置附近会出现跳跃现象，即负刚度部分的位移捕捉不到.所以采用位移载荷法，位移施加范围0～8 mm.

图3表示位移云图，其中由于碟形橡胶与承载接头的连接处存在应力集中现象，所以网格比其他地方要密集，这是为了提高仿真结果的可靠性．本模型通过上表面与中心点耦合，把中心点作为加载点，通过采集加载点的位移与反力，可得碟形橡胶模型的力与位移曲线，进一步获得刚度曲线.

图4为微凸加筋模型，由图2可知整个筋是埋在碟形橡胶的中性面上的.采用具有小弧度的加筋方式(圆弧拱高3mm)是为了防止受力加筋面屈曲而产生非连续跳跃现象，加微凸实质是对筋引入一个初始缺陷，使其屈曲发生得更加平缓.图5(a)为非微凸时的力与位移曲线，图5(b)为微凸模型，比较可知，微凸模型可以得到光滑的力与位移曲线.

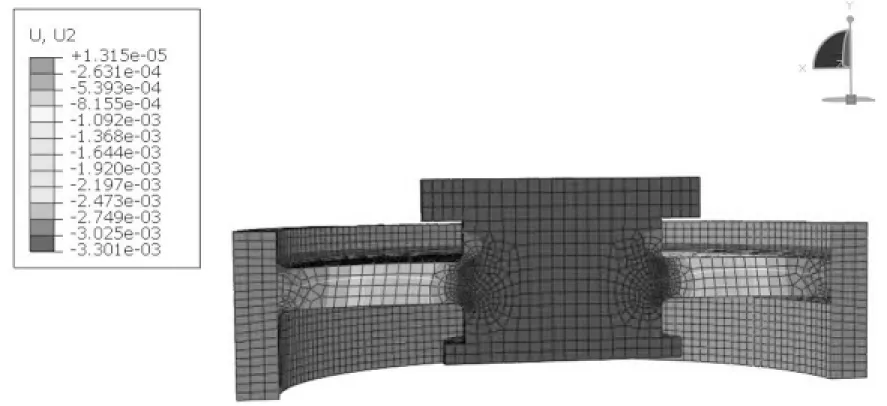
图3 碟形橡胶的有限元模型

图4 微凸加筋模型示意图

Displacement/mm

Displacement/mm

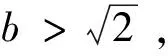
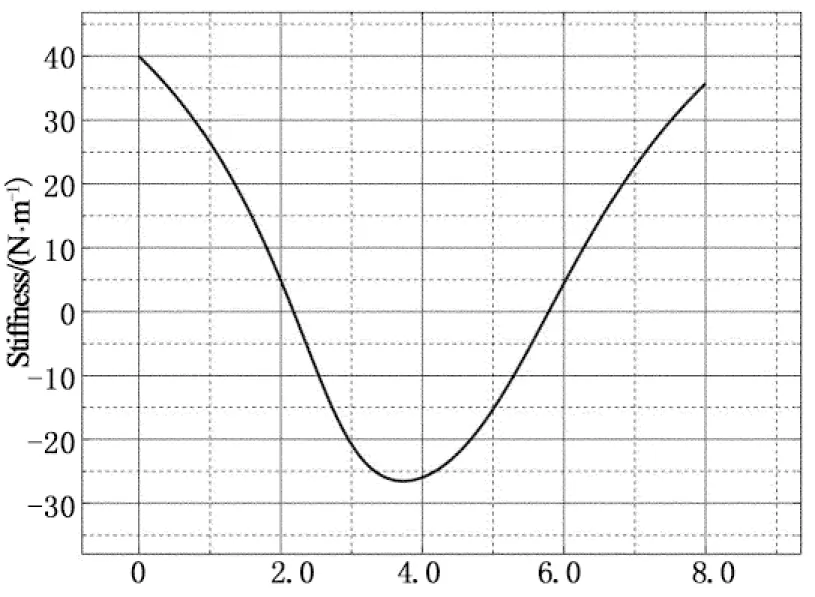
Displacement/mm

2.3 准零刚度系统的Abaqus分析

图7为碟形橡胶与竖向橡胶组合的准零刚度隔振器的三维有限元模型.在位移载荷作用下的变形位移云图表征着弹性体各点的位移分布状况.图8为力与位移曲线，图9为力对位移求导后得出的刚度曲线.图8和图9是确认组合系统是否实现准零刚度特性的依据.

图7 准零系统的有限元模型

为便于后面的准零刚度理论分析，采用只含三次项的多项式[14]来拟合有限元的力与位移曲线，利用最小二乘法拟合出力与位移的关系为：

f=k3x3=2.0918×109x3．

(4)

式中：f为系统所受外力；x为系统位移，初始位置为系统的静平衡位置.图8中的实线代表拟合曲线，虚点线代表有限元分析曲线.可以看出拟合曲线与仿真曲线在平衡点附近吻合得很好，在图8中位移-1.12mm到1.12mm之间吻合程度达99.76%.针对毫米级振动环境而言，此拟合精度足可满足工程设计要求.

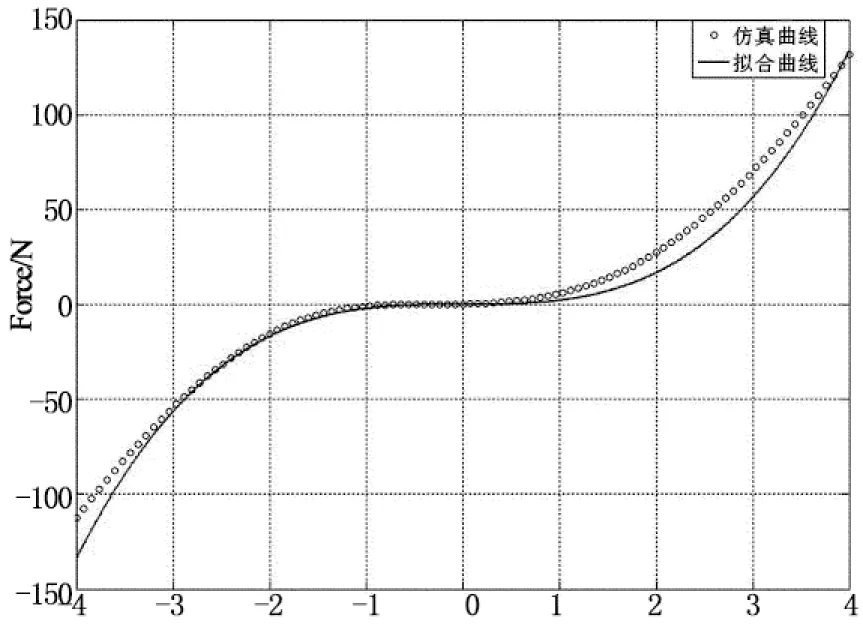
Displacement/mm

图9是通过有限元分析获得的刚度曲线(经过位移平移x=3.68 mm至平衡点).在平衡位置处，有限元分析的系统刚度实际上为135 N/m，相当于竖直橡胶刚度的0.53%.值得指出，采用有限元方法要获得绝对的零刚度是不容易的，系统组合刚度在平衡点处能降到正刚度的1%以下(接近零刚度)，符合工程设计要求.

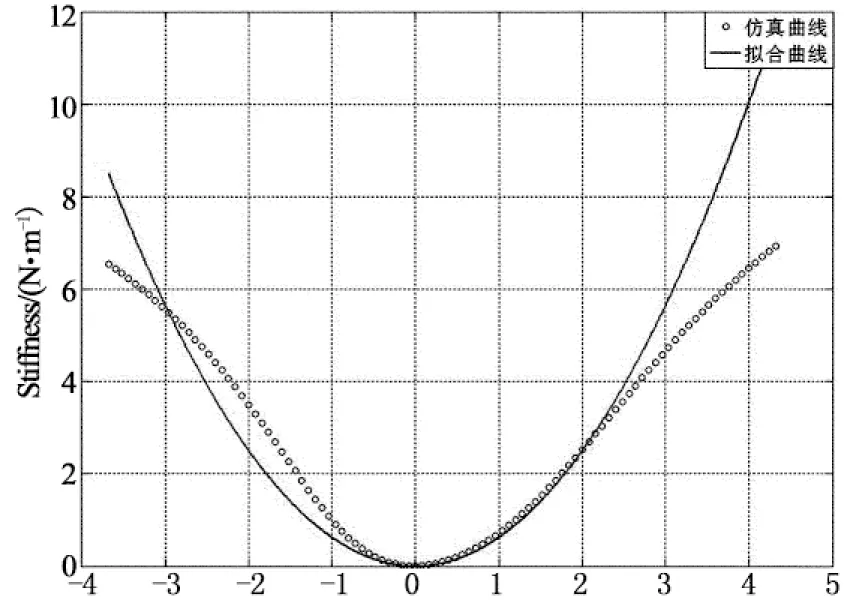
Displacement/mm

3 准零刚度系统隔振性能的理论分析

准零刚度隔振系统包括竖直橡胶和碟形橡胶、被隔振物体，并将系统结构阻尼近似为线性阻尼．当幅值为F的激振力作用于被隔振物体上时，被隔振物体会在平衡位置附近振动，如图1(b)所示.由式(4)可知:准零刚度系统回复力可由一个只含三次项的多项式表示，所以系统的运动方程可以近似表示为无线性项的达芬方程：

(5)

准零刚度隔振系统的回复力具有强非线性，利用谐波平衡法分析系统的幅频响应特性.假设系统响应频率由激励频率主导，则可以运用单谐波的方法来求解非线性的响应.因此式(5)的解可以设为y=Acos(ωt+φ)，它的幅频响应方程可表示为：

(6)

激振力的幅值为F，传递至基础的力为：

(7)

传递力的幅值为：

(8)

其中设计参数为k3=2.091 8×109N/m，m=11 kg，k=25 565 N/m.

力的传递率定义为传递到刚性基础的力的幅值和激振力的幅值的比值：

(9)

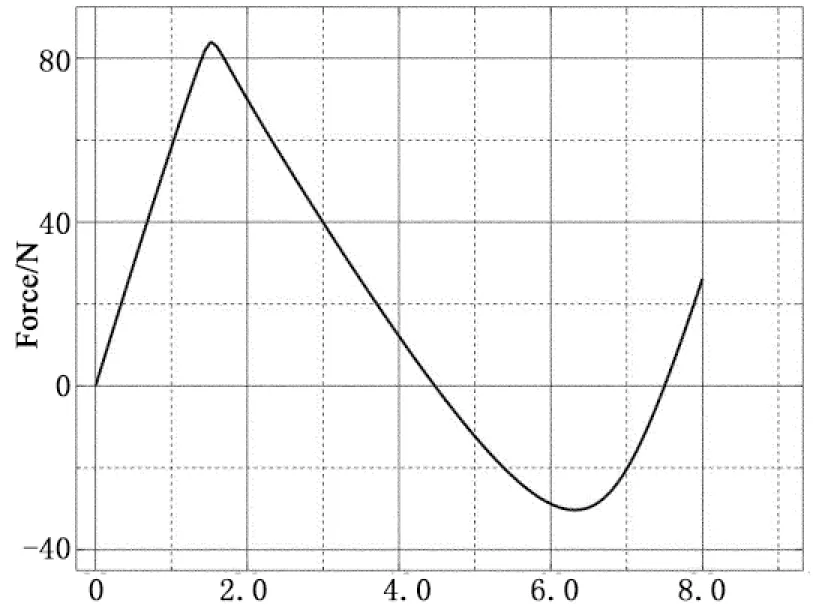
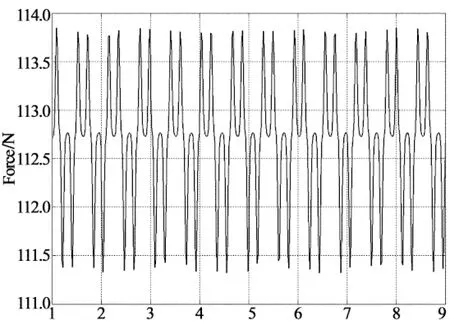
当阻尼比ζ=0.04，力幅值F=5时，系统的力传递率如图10所示.图中实线和虚线分别为准零刚度系统和相应线性系统的传递率曲线.线性系统是指撤除碟形橡胶后仅由竖直橡胶块支撑的系统.

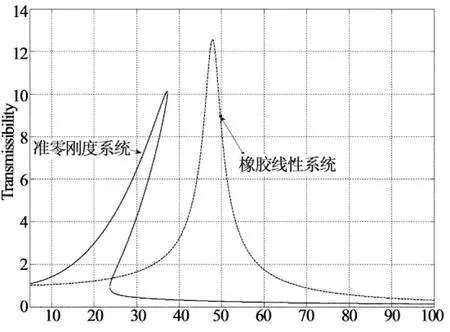
ω/(rad·s-1)

由图10可知，准零刚度系统的向下跳跃频率ω1=37 rad/s，峰值A1≈10；线性系统的固有频率ω0=48 rad/s,峰值A2=12.9.当传递率小于1时，系统具有隔振性能.从传递率曲线看，准零系统的隔振频率起始于23 rad/s，而线性系统的隔振起始于68 rad/s；且在大频率范围内准零系统的传递率远远低于线性系统.相对于线性系统而言，准零系统可以将隔振频带向低频区拓宽66.2%，这是传统方法难以企及的优越性.

4 准零刚度系统隔振性能有限元分析

当系统处于静平衡位置时，对动力学模型加载：

F=5cos(ωt)．

(10)

碟形橡胶准零刚度隔振器是典型的非线性系统，其响应成分可能出现多谐波特性，如图11显示的响应曲线.由于响应具有周期性，对于非线性隔振系统，庄表中等[14]提出力传递率的计算公式：

(11)

其中E(x2),E(y2)分别为激励与传递至基础的力的时程响应均方值.

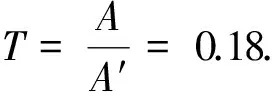
Time/s

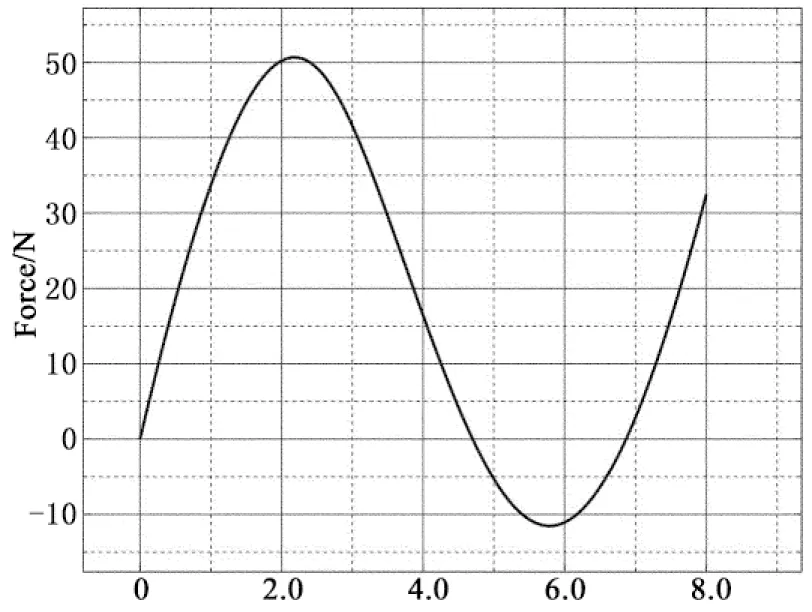
同理可得其他激励频率下的传递率曲线，见图12.准零刚度系统(实线)起始隔振频率为ω=27 rad/s，线性系统(虚线)起始隔振频率大约为ω=56 rad/s.准零刚度系统可以将隔振频带向低频区拓宽52%，且传递率远远小于线性系统.虽然图10和图12是分别基于理论分析方法和有限元数值分析方法，其结果有些微差异，但展示的隔振特性趋势基本相同.理论分析中准零刚度系统带有一个弯头部分，这部分为非线性方程的多解区间，系统响应的解取决于初始条件.进行有限元数值分析时，初始条件均取为(0, 0)，因此只能得到单一解，但从有限元分析曲线可明显观察到解的跳跃现象，即典型的非线性特性.

ω/(rad·s-1)

5 参数影响分析

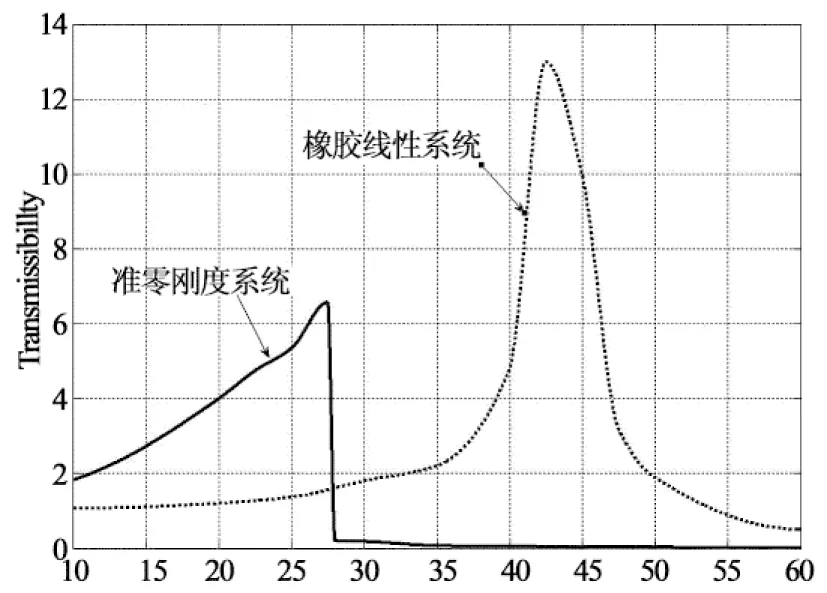
通过仿真过程得知，整个模型对刚度有影响的参数主要是筋的截面半径r和筋的数量．由图13和14可知r越大，数量越多，则该模型在静平衡位置能承受的力越大，但是刚度曲线的开口就越小，也就是准零刚度起作用的区间越窄．所以在设计碟形橡胶准零刚度隔振器时，要在承载能力与起作用区间取得平衡，也就是要选择合适的半径r与筋的数量.

在2.2节的隔振器结构尺寸情况下，仅通过改变加筋方式可以成倍提高模型在静平衡位置承载能力(被隔振质量可成倍提高)，说明该碟形准零刚度设计具有紧凑性等优点，主要是因为碟形弹簧在不改变其结构尺寸条件下可成倍提高其负刚度的特性.

Displacement/mm(a)力与位移曲线

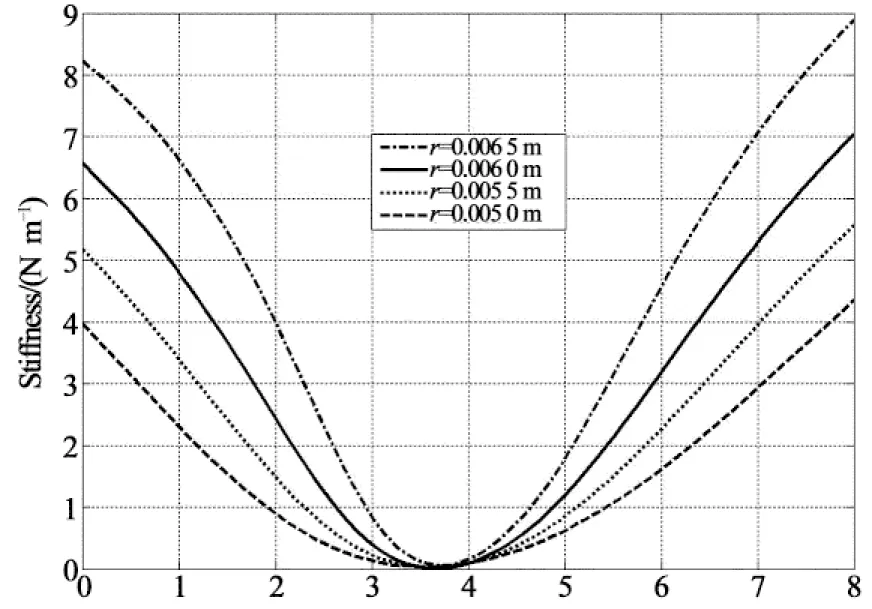
Displacement/mm(b)刚度曲线

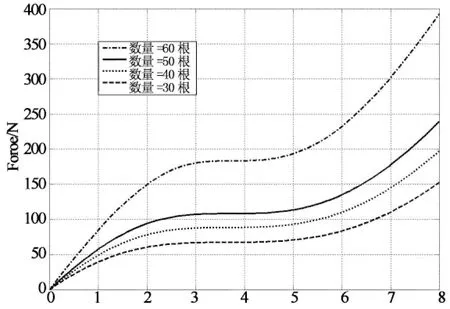
Displacement/mm(a)力与位移曲线

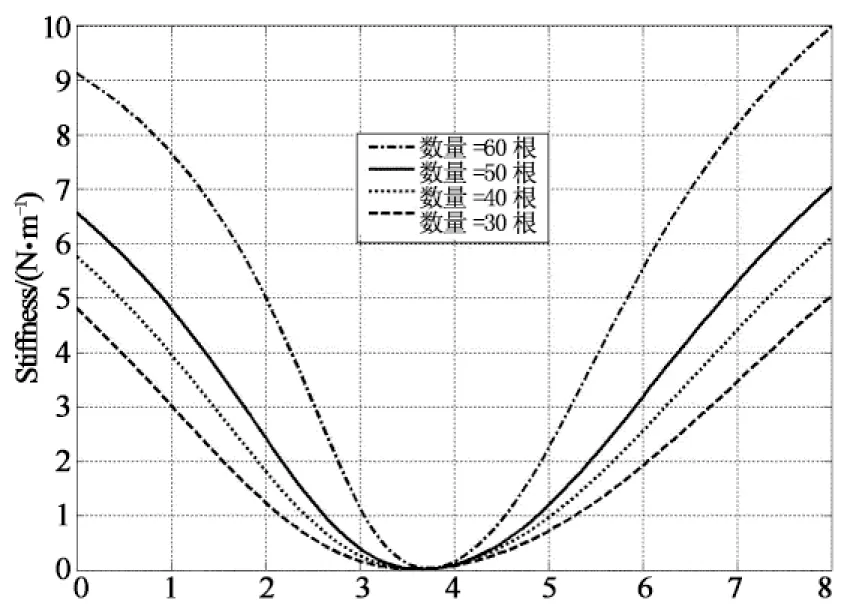
Displacement/mm(b)刚度曲线

6 结 论

本文提出了一种碟形橡胶准零刚度系统的紧凑型设计.结合碟形弹簧理论和有限元分析方法，详尽地阐述了新型准零刚度隔振器的建模方法和隔振特性.理论分析和有限元数值仿真结果均表明：1)碟形橡胶准零刚度隔振器能够实现低频隔振；2)可将隔振频带向低频区拓展50%以上；3)在隔振频带区域的隔振效率要远优于传统隔振方法.值得指出的是：本文仅描述了单层碟形设计，它可拓展到多层碟形准零刚度设计.由于受制于制造能力，目前尚未能进行实物试验验证，是个缺憾.但上述理论分析所揭示的碟形准零刚度系统的优越特性仍有学术借鉴意义.

[1]CARRELLAA,BRENNAMJ,WATERSTP.Staticanalysisofapassivevibrationisolatorwithquasi-zero-stiffnesscharacteristic[J].JournalofSoundandVibration, 2007, 301: 678-689.

[2]KOVACICI,BRENNAMJ,WATERSTP.Astudyofanonlinearvibrationisolatorwithaquasi-zerostiffnesscharacteristic[J].JournalofSoundandVibration, 2008, 315:700-711.

[3]CARRELLAA,BRENNAMJ,KOVACICI,etal. On the force transmissibility of a vibration isolator with quasi-zero-stiffness[J]. Journal of Sound and Vibration, 2009, 322: 707-717.

[4] 徐道临, 赵智, 周加喜.气动可调式准零刚度隔振器设计及特性分析[J]. 湖南大学学报:自然科学版, 2013,40(7):47-52.

XU Dao-lin, ZHAO Zhi, ZHOU Jia-xi. Design and analysis of an adjustable pneumatic vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Hunan University :Natural Sciences, 2013,40(7):47-52.(In Chinese)

[5] PLATUS D L. Negative-stiffness-mechanism vibration isolation systems[C]//Proceedings of SPIE．1999:98-105.

[6] SANTILLAN S T, VIRGIN L N, PLAUT R H. Equilibrium and vibration of a heavy pinched loop[J]. Journal of Sound and Vibration, 2005, 288: 81-90.

[7] VIRGIN L N, SANTILLAN S T, PLAUT R H. Vibration isolation using extreme geometric nonlinearity[J]. Journal of Sound and Vibration, 2008, 315: 721-731.

[8] XU Dao-lin , YU Qi-ping, ZHOU Jia-xi,etal. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2013, 332:3377-3389.

[9] XU Dao-lin, ZHANG Yue-ying, ZHOU Jia-xi,etal. On the analytical and experimental assessment of performance of a quasi-zero-stiffness isolator[J]. Journal of Vibration ad Control，2014，20：2314-2325．

[10]彭献，黎大志，陈树年. 准零刚度隔振器及其弹性特性设计[J]. 振动、测试与诊断,1997,17 (4)：44-46.

PENG Xian, LI Da-zhi, CHEN Shu-nian. Quasi-zero stiffness vibration isolators and design for their elastic characteristics[J]. Journal of Vibration, Measurement & Diagnosis, 1997, 17(4): 44-46. (In Chinese)

[11]王心龙，周加喜，徐道临. 一类准零刚度隔振器的分段非线性动力学特性研究[J].应用数学与力学,2014,35(1):50-62.

WANG Xin-long, ZHOU Jia-xi, XU Dao-lin. On piecewise nonlinear dynamic characteristics of a new-type quasi-zero-stiffness vibration isolator with cam-roller-spring mechanism[J]. Applied Mathematics and Mechanics,2014,35(1):50-62.(In Chinese)

[12]ZHOU N, LIU K. A tunable high-static-low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration,2010,329：1254-1273.

[13]秦大同，谢里阳.现代机械设计手册[M].北京：化学工业出版社,2013.

QIN Da-tong, XIE Li-yang. Modern handbook of mechanical design[M].Beijing: Chemical Industry Press,2013.(In Chinese)

[14]庄表中，王建华，邢 宏. 关于非线性隔振系统动态特性的描述方法[J].振动与冲击,1986,5(3):33-37.

ZHUANG Biao-zhong, WANG Jian-hua, XING Hong. The description method about the dynamic characteristics of nonlinear vibration isolation system[J]. Journal of Vibration and Shock, 1986,5(3):33-37.(In Chinese)

Design and Analysis of a Disc Rubber Vibration Isolator with Quasi-zero-stiffness Characteristic

XU Dao-lin†，ZHOU Jie, ZHOU Jia-xi , ZHANG Jing

(State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan Univ, Changsha，Hunan 410082, China)

A disc rubber vibration isolator with quasi-zero stiffness (QZS) was designed, and the characteristics of vibration isolation were studied. The QZS isolator was devised by assembling a reinforced disc rubber with negative stiffness in parallel with a vertical rubber cylinder with positive stiffness. By using Finite Element Analysis (FEA), the geometrical parameters of the reinforced disc rubber and the vertical rubber cylinder were achieved to ensure that the isolator's stiffness is close to zero at the static equilibrium position. And then, the characteristics of restoring force were analyzed, and the expression of restoring force was given as a polynomial only having cubic item by fitting the FEA simulations data. Moreover, the equation of motion of the vibration isolation system was obtained, and the isolation performance was evaluated theoretically based on Harmonic Balanced method, which was compared with that by using dynamic FEA. The results have shown that the QZS isolator significantly outperforms the corresponding linear one.

quasi-zero-stiffness； disc rubber； vibration isolator； low-frequency vibration isolation

1674-2974(2015)08-0022-07

2014-07-07

国家自然科学基金资助项目(11102062)，National Natural Science Foundation of China(11102062) ；高等学校博士学科点专项科研基金资助项目(20130161110037，20110161120040)；中央高校基本科研业务费资助项目

徐道临(1958-)，男，浙江宁波人，湖南大学教授，博士生导师

†通讯联系人，E-mail: dlxu@hnu.edu.cn

O322；O328

A