随机对照试验不依从数据分析方法的比较研究

哈尔滨医科大学公共卫生学院（150086） 陈永杰 张秋菊 王玉鹏 肖亚明 刘美娜

随机对照试验不依从数据分析方法的比较研究

哈尔滨医科大学公共卫生学院（150086） 陈永杰 张秋菊 王玉鹏 肖亚明 刘美娜△

目的比较依从者的平均因果效应（CACE）、意向性分析（ITT）、遵循研究方案分析（PP）和接受干预措施分析（AT），在分析随机对照试验不依从数据的效果，探索各种方法的适用条件，为实际数据分析提供科学依据。方法通过SAS软件模拟产生不依从数据，处理措施的因果效应使用CACE、ITT、PP和AT进行估计，以平均偏倚、均方根误差、标准误和检验效能作为评价指标，比较各种方法的估计效果。结果在各种参数组合下，以平均偏倚、均方根误差和检验效能作为评价指标，CACE的估计效果均优于ITT、PP和AT。依从率低于50%时，CACE估计的标准误低于PP，高于ITT和AT；依从率高于50%时，CACE估计的标准误均低于ITT、PP和AT。结论当满足CACE模型假设时，CACE估计随机对照试验不依从数据因果效应的效果优于三种传统分析方法，能够提供更加稳健、无偏的处理效应估计值。

随机对照试验 不依从 CACE ITT分析 PP分析 AT分析

随机对照试验（random ized controlled trials，RCT）是目前公认的估计干预措施因果效应的金标准［1］。然而，以人为研究对象的随机对照试验常遇到两个主要问题：不依从（non-compliance）和失访（loss to follow-up）［2－6］。分析带有不依从现象的随机对照试验的传统方法包括：意向性分析（intention-to-treat analysis，ITT）、接受干预措施分析（as-treated analysis，AT）和遵循研究方案分析（per-protocol analysis，PP）。三种方法均存在不同程度的局限性，ITT保留了随机化分组，分析的是分配处理的效应，事实上接受处理的效应是研究者感兴趣的［7－9］；PP分析删除不依从的个体，当不依从率较高时会高估处理效应，增大Ⅰ类错误［10］；AT分析按照实际接受处理的情况分析，破坏了随机化分组，引入选择偏倚。因此，三种传统分析方法在估计处理措施的因果效应时并不能给出一个无偏的估计［5－6，11］。本文介绍另一种方法——依从者的平均因果效应（complier average causal effect，CACE）［2，6，12］，通过模拟实验与ITT、PP和AT比较，评价各方法估计随机对照试验不依从数据因果效应的效果。

基本原理与方法

1．基本原理

根据主分层的思想，按照个体分配到的处理（Z）和实际接受的处理（D）把受试者分为四层：依从者（compliers）、从不接受处理者（never-takers）、总是接受处理者（always-takers）和总是接受相反处理者（defiers）［12－13］。CACE主要关注依从者，估计依从者的因果效应，模型表示为：

μ1c是处理组依从者的平均潜在结果，μ0c是对照组依从者的平均潜在结果。

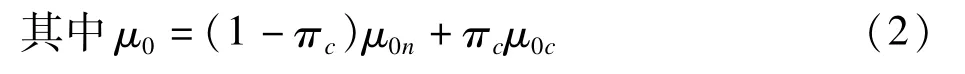
πc表示人群中依从者所占的比例，μ0n是对照组不依从者的平均潜在结果。

由（1）和（2）可得

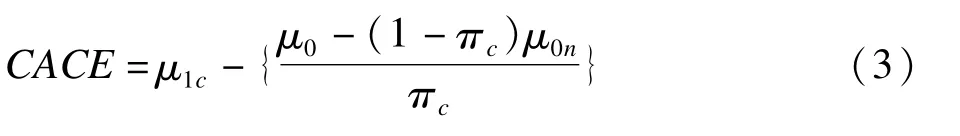
2．模型假设

随机对照试验中，对照组通常是空白对照或者安慰剂对照，个体是否依从于试验并不能完全观测到，故公式（3）不可识别。估计CACE时需要建立五个基本假设［13］：

（1）SUTVA假设（stable unit treatment value assumption）：指研究个体间不存在关联性，即个体A是否接受处理与个体B无关；每个个体仅有一种结果被观测到，该假设又称一致性假设（consistency assumption）。

（2）随机化假设：即随机分组，此假设在随机对照试验中是成立的。

（3）排除限制性假设（exclusive restriction assumption，ER）：在随机分组中，总是接受处理者和从不接受处理者的处理效应为零，同时μ0n＝μ1n。

（4）单调性假设（monotonicity assumption）：在随机对照试验中，总是接受相反处理者不存在。

（5）非零分子假设（nonzero numerator assumption）：指研究人群中一定存在依从者。

在五个模型假设成立的前提下，可将总是接受相反处理者排除；由于随机对照试验的对照组人群通常不能获得处理措施，可将总是接受处理者排除。以下分析都是针对依从者（compliers）和从不接受处理者（never-takers）两层人群。

根据以上假设CACE表示为：

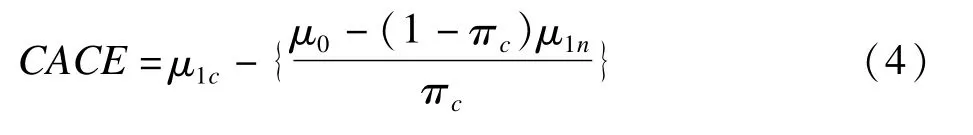
3．参数估计

CACE参数估计通过广义线性潜在混合模型（generalized linear latent and mixed model，GLLAMM）［14］实现。CACE参数估计过程如下：

（1）结果模型

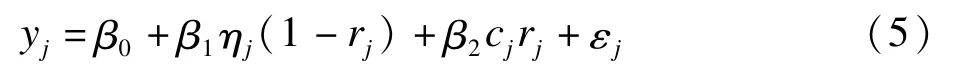
yj表示第j个个体的结果测量值；rj为随机分组变量，rj＝1表示第j个个体分到处理组，rj＝0表示分到对照组；cj为依从变量，cj＝1表示第j个个体为依从者，cj＝0表示不依从者；ηj为潜变量，取值1和0。

由公式（1）和（5）可得：

（2）依从模型

通过指示变量d把模型（5）和（7）联立

（3）联合模型：

通过对模型（8）进行参数估计得到β1和β2，由公式（6）可得CACE估计值。

不依从现象常伴随数据缺失，在考虑数据缺失机制后获得CACE估计值会更加准确。假设数据缺失机制为潜在可忽略（latent ignorability，LI），CACELI参数估计过程如下：

（1）缺失数据模型

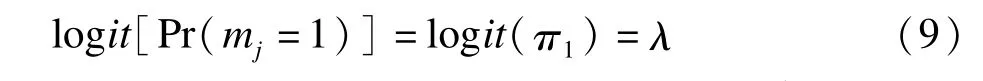
通过指示变量d把模型（5），（7），（9）联立

（2）联合模型：

模拟实验

通过模拟实验比较CACE、ITT、PP和AT在分析随机对照试验不依从数据时的优劣，从样本含量、依从率和缺失率三方面观察每种方法的估计效果，并探索各种方法的适用条件。

1．参数设置

样本含量设置为80、150和400；依从率设置为40%、60%和80%；缺失率设置为10%和30%；数据缺失机制设置为随机缺失（m issing at random，MAR）；处理效应真实值设置为1；基线测量变量服从N（－0．35，1．462）；研究对象以P（Zi＝1）＝0．5的概率随机分配到处理组和对照组。

结果变量的生成模型为：Yi＝β0＋β1xi＋β2ZiCi＋εi；依从变量的生成模型为：logitPci＝ln（Pci／（1－Pci））＝β0＋βcxi；缺失观测的生成模型为：logitPmi＝ln（Pmi／（1－Pmi））＝βm0＋βm1xi＋βm2Ci。各种参数组合重复模拟1000次。

2．评价指标

估计效果评价指标包括偏差（bias）、均方根误差（RMSE）、标准误和检验效能（power）。平均偏倚是估计值和真实值之间差值的平均数，该值越接近0表示估计的偏倚越小；均方根误差综合反应估计的方差与偏倚，该值越接近0表示估计越准确；标准误表示估计的精确度，该值越小表示估计的波动越小；检验效能反应估计的把握度，该值越接近100%表示犯Ⅱ类错误的概率越小。模拟实验主要通过SAS9．2和STATA12．0进行，CACE估计通过GLLAMM模型实现，ITT、PP和AT通过线性回归分析实现。

3．结果

表1和表2分别描述了缺失率为10%和30%时的模拟实验结果，CACE、ITT、PP和AT的平均偏倚和均方根误差均随着样本含量的增加、依从率的增高而逐渐变小；在各种参数组合下，CACE的估计效果均优于ITT、PP和AT。

表1 缺失率为10%时各方法的模拟实验结果

表2 缺失率为30%时各方法的模拟实验结果

图1描述了四种方法估计的标准误随着样本含量的增加逐渐变小的趋势；CACE和PP的标准误随着依从率的增高明显降低，ITT和AT基本保持不变；依从率低于50%时，CACE的估计效果优于PP，依从率高于50%时，CACE的估计效果优于ITT、PP和AT。

图1 各参数组合下每种方法估计值标准误的模拟实验结果

图2描述了四种方法的检验效能随着样本含量的增加逐渐增大的趋势，ITT和AT在样本含量为400时检验效能增加明显；在各种参数组合下ITT和AT的检验效能始终保持一致；样本含量为80、150和400时，CACE的检验效能均优于ITT、PP和AT，样本含量为400时，PP的检验效能与CACE接近。

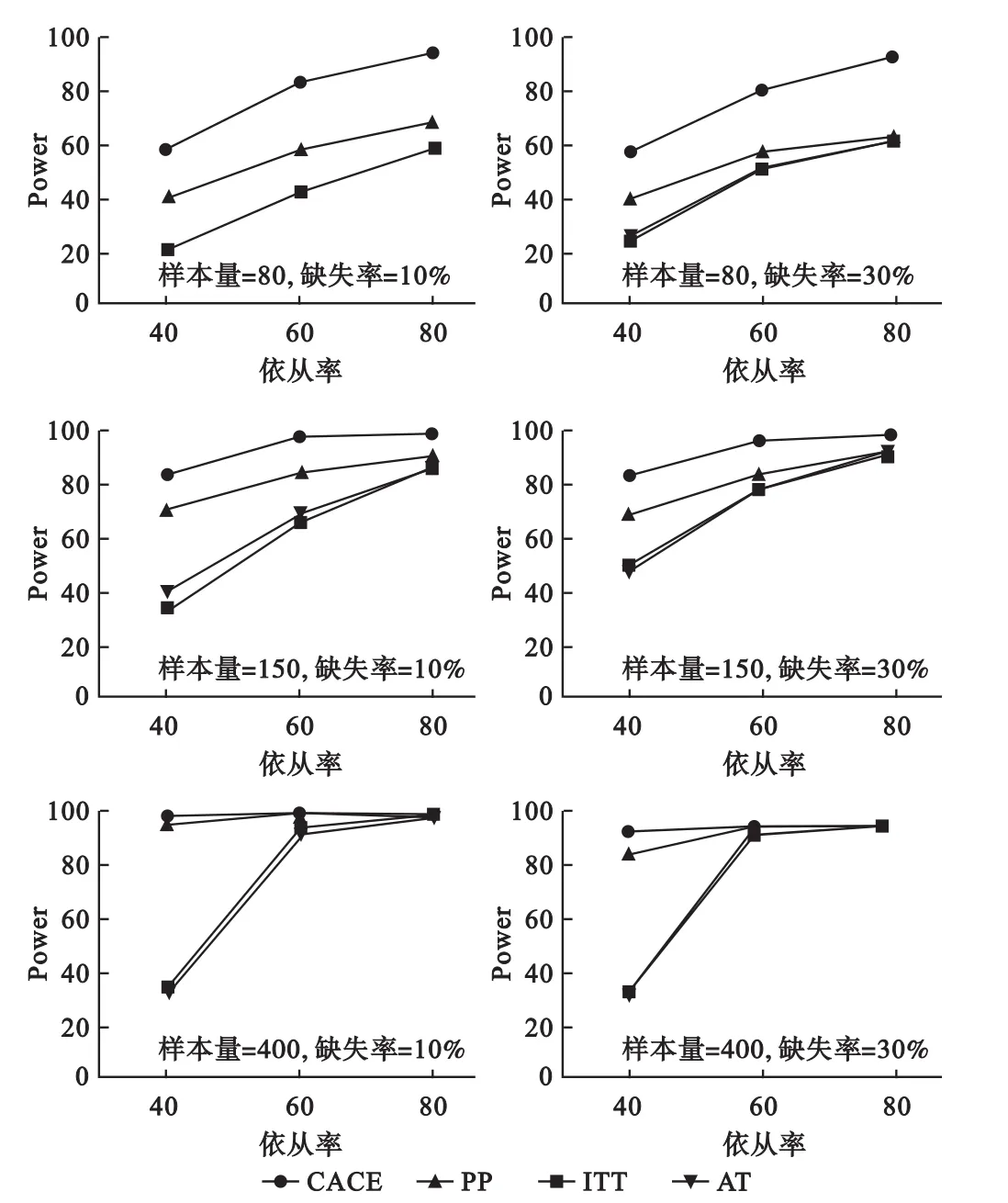
图2 各参数组合下每种方法检验效能的模拟实验结果

讨 论

CACE充分利用不依从和缺失数据的信息，通过处理组可观测的信息推断对照组不可观测的信息，利用潜变量进行参数估计，综合所有的信息对处理措施的因果效应进行估计，从而得到一个真实可靠的结论。本研究通过模拟实验证实，在各种参数组合下CACE的估计效果均优于ITT、PP和AT，且每种方法的估计效果随着样本含量的增加、依从率的增高而逐渐趋于稳健。因此建议在数据分析方法选择时，应优先采用CACE对不依从数据进行分析。

CACE建立在五个模型假设基础上，分析实际数据时，模型假设是否成立会不同程度影响结果的准确性。随机对照试验设计可以保证假设1、2、4和5成立，但假设3成立与否是无法检验的。因此，对实际数据分析后有必要对模型进行灵敏度分析（sensitivity analysis），检验模型假设不成立时参数的估计结果是否会发生显著性变化，对分析结果的准确度有一定的把握［6］。CACE目前主要用于两组间的比较，多组间的比较只能给出大致的区间估计［4，7］。因此，CACE多组间比较有待于进一步研究。

本研究通过模拟实验证实CACE分析不依从数据的效果优于三种传统的分析方法，为研究者提供了一种新的分析不依从数据的方法。实际中，使用CACE分析随机对照试验不依从数据的同时，应结合ITT和PP的分析结果，综合所有的信息对试验下结论并给出一个令人信服的结果解释，这样得到的结论才更加准确可靠，估计的因果效应才更接近处理措施的真实值。

［1］张熙．多重填补方法估计存在不依从与缺失值的随机对照试验的因果效应．上海：复旦大学，2012．

［2］Imbens GW，Rubin DB．Bayesian inference for causal effects in randomized experiments with noncompliance．The Annals of Statistics， 1997：305-327．

［3］Frangakis CE，Rubin DB．Addressing complications of intention-totreat analysis in the combined presence of all-or-none treatment-noncompliance and subsequentm issing outcomes．Biometrikam，1999，86（2）：365-379．

［4］Cheng J，Small DS．Bounds on causal effects in three-arm trials with non-compliance．Journal of the Royal Statistical Society：Series B（Statistical Methodology），2006，68（5）：815-836．

［5］Peng Y，Little RJ，Raghunathan TE．An extended general location model for causal inferences from data subject to noncompliance and m issing values．Biometrics，2004，60（3）：598-607．

［6］Jo B．Modelm isspecification sensitivity analysis in estimating causal effects of interventions with non-compliance．Statistics in medicine，2002，21（21）：3161-3681．

［7］Little RJ，Long Q，Lin X．A comparison of methods for estimating the causal effect of a treatment in random ized clinical trials subject to noncompliance．Biometrics，2009，65（2）：640-649．

［8］Hirano K，ImbensGW，Rubin DB，etal．Assessing the effectof an influenza vaccine in an encouragement design．Biostatistics，2000，1（1）：69-688．

［9］Welsh AW．Random ised controlled trials and clinicalmaternity care：moving on from intention-to-treatand other simplistic analyses of efficacy．BMC pregnancy and childbirth，2013，13：15．

［10］Dodd S，White IR，W illiamson P．Nonadherence to treatment protocol in published random ised controlled trials：a review．Trials，2012，13：84．

［11］Schwartz S，Li F，Reiter JP．Sensitivity analysis for unmeasured confounding in principal stratification settings with binary variables．Statistics in medicine，2012，31（10）：949-962．

［12］Angrist JD，Imbens GW，Rubin DB．Identification of causal effects using instrumental variables．Journal of the American statistical Association，1996，91（434）：444-455．

［13］Jo B，Ginexi EM，Ialongo NS．Handling m issing data in randomized experimentswith noncompliance．Prevention Science，2010，11（4）：384-96．

［14］Skrondal A，Rabe-Hesketh S．Some applicationsof generalized linear latent and mixed models in epidemiology：repeated measures，measurement error and multilevelmodeling．Norsk epidem iologi，2003，13（2）：265-278．

（责任编辑：郭海强）

Com parison of Methods Analyzing Non-com pliance Data of Random ized Controlled trial

Chen Yongjie，Zhang Qiuju，Wang Yupeng，etal．（DepartmentofBiostatistics，PublicHealthCollege，HarbinMedicalUniversity（150086），Harbin）

ObjectiveTo compare the performance of complier average causal effect（CACE）with thatof intention-totreat analysis（ITT），per-protocol analysis（PP），and as-treated analysis（AT）in estimating treatment effect of random ized controlled trialwith non-compliance，to explore the application conditions of eachmethod，and to provide scientific evidence for analyzing practical data．MethodsNon-compliance data was simulated using SAS．CACE，ITT，PP and AT were used to estimate treatment effect and their performances were evaluated using bias，root mean square error（RMSE），standard error，and power．ResultsFor all combinations of parameters，the performance of CACE was better than that of ITT，PP and AT in bias，RMSE and power．When compliant rate was less than 50%，the performance of CACEwas better than thatof PP in standard error，butworse than that of ITT and AT；when more than 50%，CACE was the best．ConclusionWhen themodel assumptions hold，CACE is better atestimating causal effect than ITT，PP and AT，and can provide an unbiased and robustestimation of treatment effect．

Random ized controlled trial；Non-compliance；Complier average causal effect；Intention-to-treat analysis；Per-protocol analysis；As-treated analysis

△通信作者：刘美娜