动态矩阵算法在水箱液位控制中的应用

Application of Dynamic Matrix Algorithm in Level Control of Water Tank

叶　昊　侯　艳　马　光

(北华航天工业学院电子工程系，河北 廊坊　065000)

动态矩阵算法在水箱液位控制中的应用

Application of Dynamic Matrix Algorithm in Level Control of Water Tank

叶昊侯艳马光

(北华航天工业学院电子工程系，河北 廊坊065000)

摘要：针对先进控制技术在下位控制系统中的应用问题，采用水箱模拟工业控制中常见的一阶被控对象。通过S7-300控制器，采用SCL语言编写矩阵运算功能块，实现了动态矩阵控制算法。水箱液位定值试验表明，在正常及扰动状态下，动态矩阵控制算法都取得了良好的控制效果。对于动态品质要求较高的控制系统，动态矩阵控制的实现效果明显优于传统PID控制。

关键词：下位机结构化控制语言惯性环节水箱液位控制动态矩阵控制(DMC)

Abstract：Be aimed at the issue of applying advanced control technology in subordinate control systems, the water tank is adopted to emulate the commonly seen 1st order controlled object in industrial control. Through S7-300 controller, the matrix operation functional block is programmed by using SCL language to implement dynamic matrix control algorithm. The test of water tank level indicates that in normal and disturbed condition, excellent control effects are obtained. For control systems requesting high dynamic quality, the effect of dynamic matrix control is obviously better than traditional PID control.

Keywords：Hypogynous machineStructured control languageInertial linkLevel controlDynamic matrix control(DMC)

0引言

系统成本、通信的可靠性及控制精度一直是衡量一个控制系统优劣的重要指标。数据采集与监视控制系统[1](supervisory control and data acquisition，SCADA)通常采用上位、下位的监控模式，通过各种总线进行通信。总线系统的建设在硬件方面、安全性方面均需增加成本，同时，通信系统的实时性也面临考验。

预测控制基于模型预测的启发式控制算法，采用输入/输出的非参数阶跃响应或脉冲响应模型作为预测模型。该模型通过测试比较容易得到，并且算法本身对模型精度的要求并不高。但由于算法实现时涉及大量的数学运算，因此预测控制通常运行于上位监控系统中。动态矩阵控制(dynamic matrix control,DMC)是预测控制的一种。对于可编程控制器，可否有效完成这些矩阵运算，可运算矩阵的阶数是多少，控制算法的实现效果如何，这些都是本文要探讨的问题。

1试验硬件的组成

试验系统现场设备中，采用水作为试验介质，整个管路由上海凯士比水泵供水，通过西门子MM440变频器实现对水泵的变频控制。试验管道上安装有大禹阀门，通过SIPART PS2智能电气阀门定位器控制阀门开度的大小，从而决定水箱液位的高低；水箱液位高度采用SITRANS P系列压力变送器(带有PA功能)测量，并将测得的压力数据转换成液位值。

控制柜中，采用S7-300控制器作为下位机，连接有DP/PA耦合器，实现与现场PA仪表的通信。控制器与上位机的通信采用CP343-1IT以太网模块，实现数据在上位系统中的实时显示。上位机中安装有WinCC监控软件，并制作相应的监控画面。

2控制方案的实现

控制方案实现时，可采用固定阀门开度，通过变频调速控制水泵转速来决定整个系统的供水量，进而决定水箱液位的高度；也可采用恒压供水，通过改变管道阀门开度的方式决定液位的高度。本设计中采用了后一种方案。

3动态矩阵算法原理及模型测试

动态矩阵控制算法[2]原理部分参见参考文献[2]，在此不再重复叙述。

模型测试部分采用开环阶跃响应曲线法[3-4]。测试时，将系统置于手动状态，将阀门开度从20%变化到30%，得到实测数据，如表1所示，则单位阶跃响应数据为其实测数据的1/10。

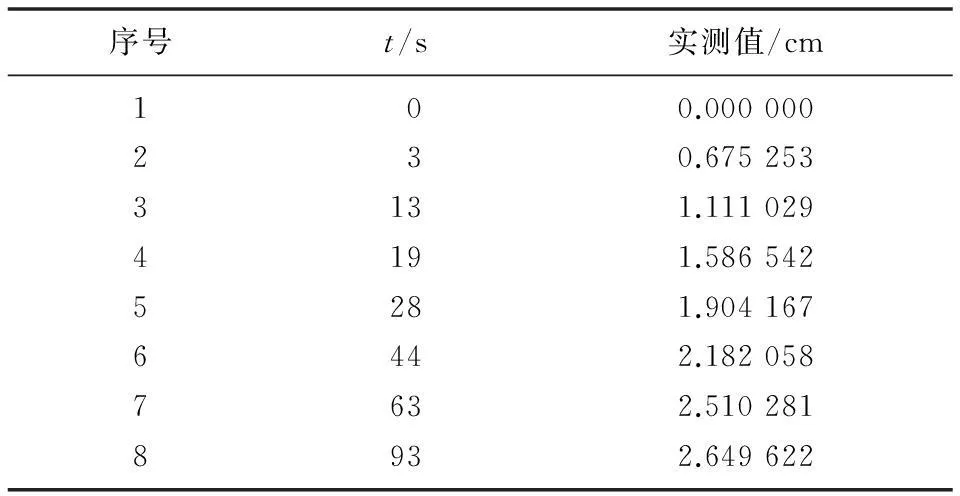
表1　开环响应实测数据值

在Matlab下采用非线性最小二乘拟合方式，得到传递函数为：

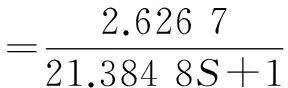
(1)

求得合误差为0.134 5。

将式(1)在时域中展开，可计算得到单位阶跃函数下的响应数据，如表2所示。

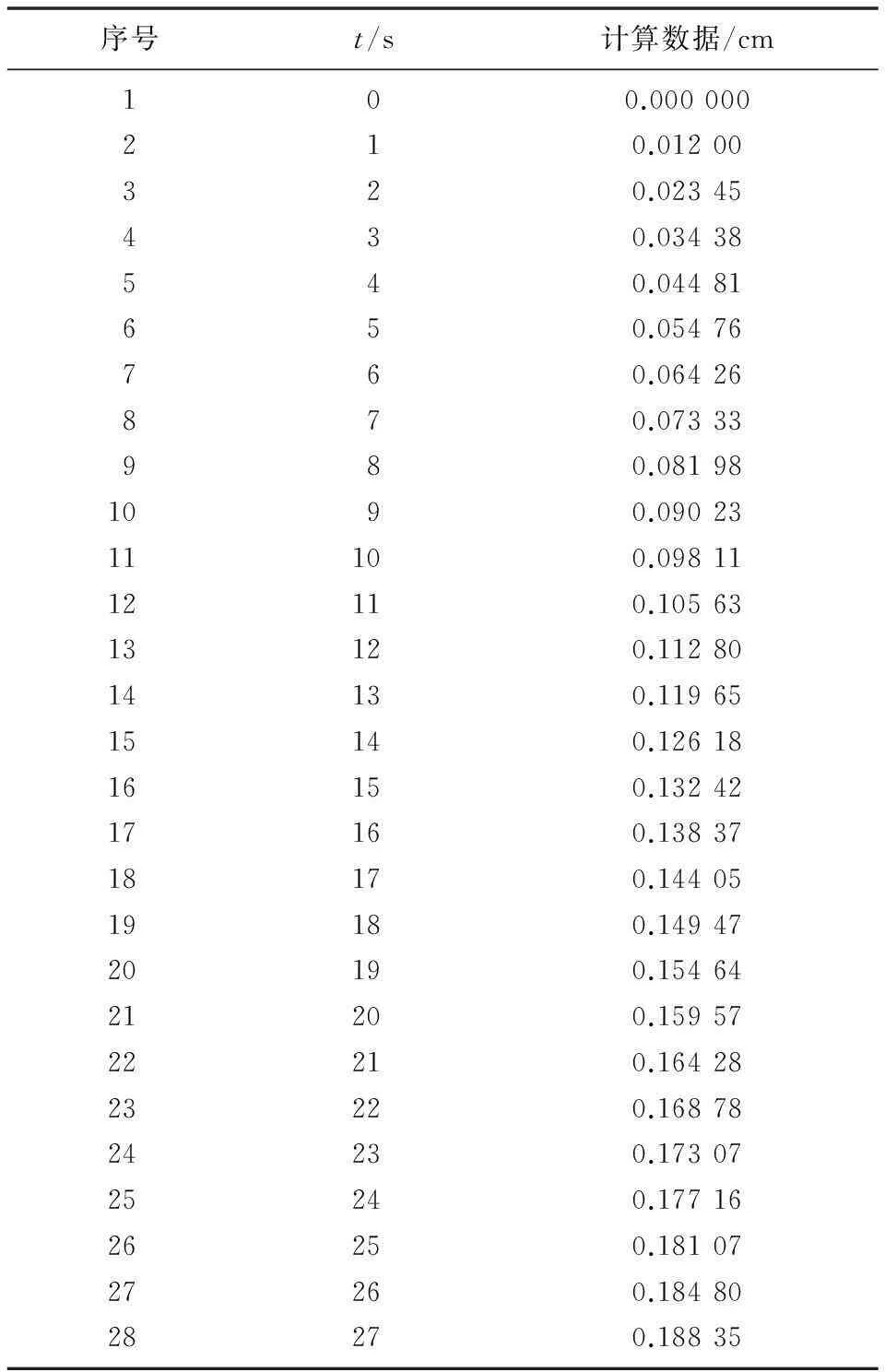
表2　单位阶跃响应数据

表2中仅列出了前27 s的计算数据，后段阶跃响应的数据可按照相同方法计算得到。

4算法实现部分

4.1　矩阵数据类型的定义

矩阵运算部分采用SCL语言，所以需在Step7环境下安装S7_SCL软件包。

矩阵数据类型定义如下。

TYPE MATRIX

STRUCT

hang: INT := 0;

lie: INT := 0;

elemente: ARRAY[1..20,1..20] OF REAL;

END_STRUCT

END_TYPE

4.2　矩阵运算的实现

实现时，需在Sources文件夹下建立SCL Source，进行算法设计，如加法运算。

(1) FC功能的建立

建立FC功能的目的是实现矩阵的加法运算功能。

FUNCTION Add : VOID

VAR_INPUT

MxA: MATRIX;

MxB: MATRIX;

END_VAR

VAR_OUTPUT

MxC: MATRIX;

END_VAR

VAR_TEMP

line, list: INT;

END_VAR

BEGIN

IF (MxA.hang= MxB.hang) AND (MxA.lie =MxB.lie) THEN MxC.hang:= MxA.hang; MxC. lie:= MxA. lie;

FOR line:=1 TO MxA.hang DO

FOR list:= 1 TO MxA.lie DO

MxC.elemente[line,list]:= MxA.elemente[line,list]+MxB.elemente[line,list];

END_FOR;

END_FOR;

ELSE

MxC.hang:=0;

MxC.lie:= 0;

END_IF;

END_FUNCTION

在Symbols中，将用SCL编写的函数名称与FB或FC联系起来，其中Symbol为编写的SCL函数名称，如Add;Address为FB/FC名称，如FC8。在SCL编写环境下进行编译，这样在Blocks下即生成了相对应的FB/FC功能块。每次修改Sources文件夹下的SCL Source源代码后，需重新进行编译。本设计中将上述SCL代码生成了一个FC。

(2) 加法运算功能块的实现

定义一个FB功能块，通过在OB组织块中的调用，以此实现具体的数学运算功能。

FUNCTION_BLOCK MxAdd

VAR

n:int;

m:int;

END_VAR

VAR

Am, Bm, Cm : MATRIX;

END_VAR

Am.hang := n;

Am.lie:= m;

Bm.hang:= n;

Bm.lie:= m;

Add( MxA:= Am, MxB:= Bm, MxC:= Cm);

END_FUNCTION_BLOCK

DATA_BLOCK DIMxAdd MxAdd

BEGIN

END_DATA_BLOCK

编译生成一个FB功能块及对应的DB背景块。其中FB及其对应的DB均需在Symbols中进行连接，如MxAdd功能块的Address为FB8，DIMxAdd背景数据块的Address为DB8。

进行数据运算时，可在DB块中直接修改DB8.DBB0及DB8.DBB2中的数据，以此来定义矩阵的维数。通过使用SFC20“BLKMOV”，将拟运算的数据写入DB8的Am元素和Bm元素。

4.3　DMC算法参数的选择

考虑到DMC运算中的阶跃响应系数ai需包括阶跃响应曲线的主要动态部分[5-7]，如果采样周期过小，则向量ai的长度较长，这会造成矩阵A阶数较大。对于S7-300这样的控制单元，可能无法完成矩阵的运算，所以在此取采样时间为5 s。

A为阶跃响应系数ai组成的P×M矩阵。P大小取决于ai的长度，实际取值时应小于10，否则矩阵过大，控制器无法完成运算。

当P=3时，ai=[0.054 76，0.098 11，0.132 42]；P=7时，ai=[0.054 76，0.098 11，0.132 42，0.159 57，0.181 07，0.198 08，0.211 55]；

误差权矩阵Q=diag(1,1,1,…，1)P×P；

控制时域M=2或3；

控制权矩阵R为一个M×M的方阵；

校正参数hi为全1的N维向量。

4.4　dT矩阵的计算

在计算dT时，由于涉及逆运算的问题，会消耗大量的PLC系统资源，在实际PLC控制器中无法完成，可在S7-300编程环境下自带的仿真软件S7-PLCSI或Matlab软件下进行离线计算。

dT矩阵与R值有很大的关系。当其他参数均设计完成后，R值成为控制算法唯一的对外接口。修改R值可以限制控制器的输出量，防止控制器的运算结果超出执行机构可执行的有效数据范围。

5试验效果分析

试验过程中[8-10]，通过改变孔板开度的方法来模拟用水量的扰动(用水量增加或减少)。

(1) 运算矩阵为3阶，P=3，M=2

取R=0.01，计算得到dT=[2.168 462 2.124 94 2.090 193]。考虑到试验开始时，由于液位设定值与液位当前值之间的偏差过大，通过一定算法得到的输出数据可能超出执行机构的数据执行范围，从而使DMC算法的模式失配，所以在控制初始段仍采用PID控制规律，在两个控制周期后切换到DMC控制算法模式。水箱液位实际监控曲线，如图1所示。

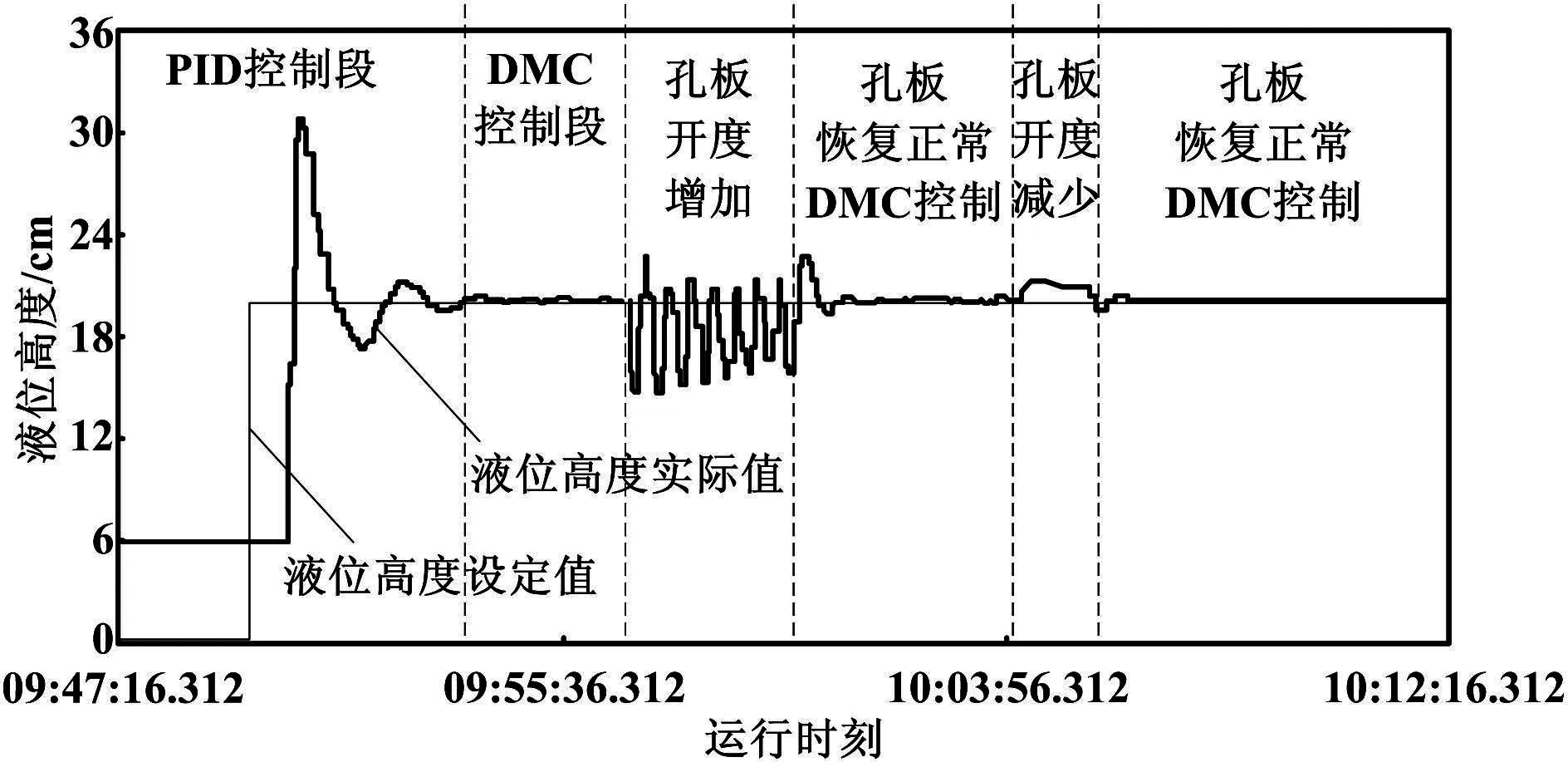
图1　水箱液位跟踪变化曲线1

(2) 运算矩阵为7阶，P=7，M=3

取R=0.03，计算得到dT=[0.933 057 61.057 863

0.776 636 60.553 902 80.377 8750.238 348 60.128 032]，试验过程同(1)。水箱液位实际监控曲线2如图2所示。

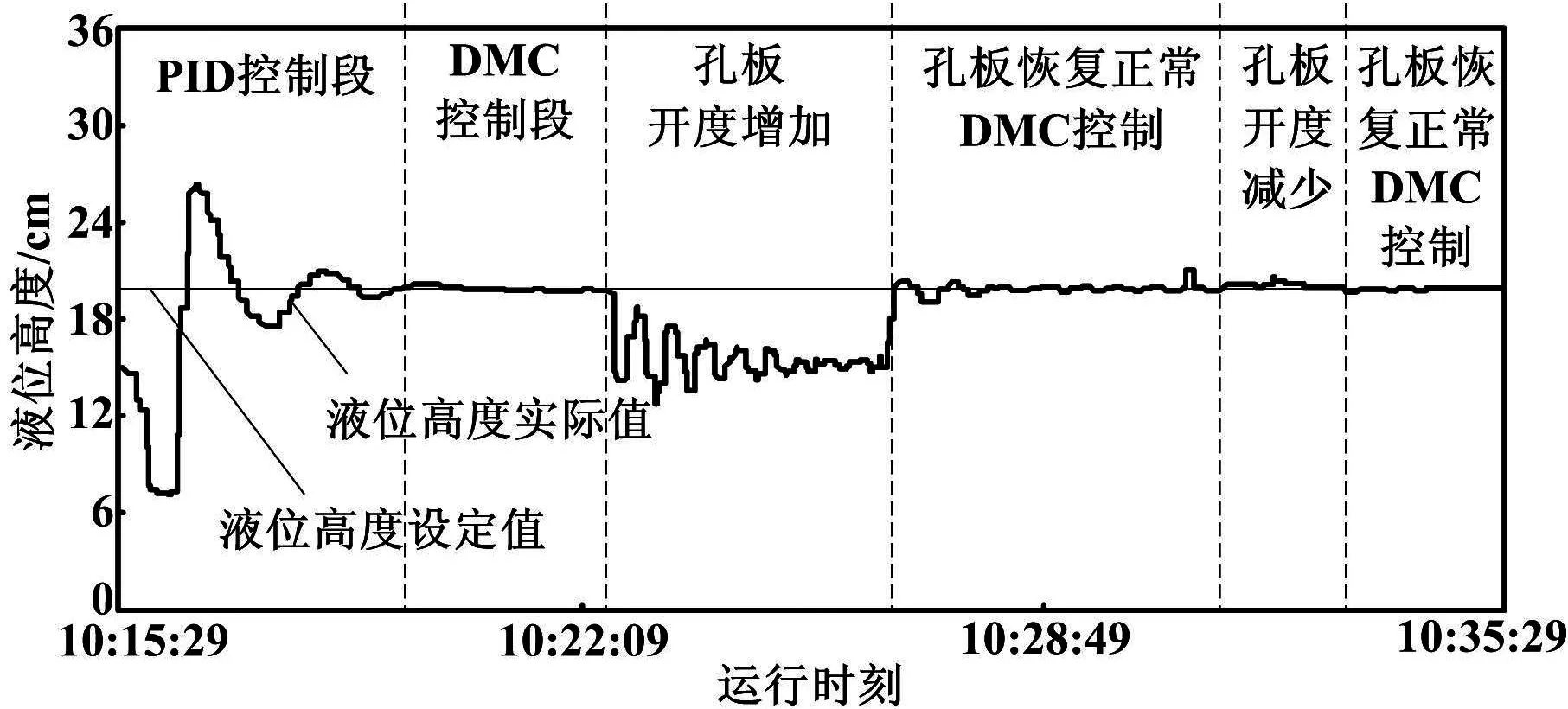
图2　水箱液位跟踪变化曲线2

分析上述两个试验结果可以看出，对于不同阶数的矩阵，需修改R的取值，并重新计算dT矩阵。通过大量的试验可以看出，当扰动出现时，液位跟踪设定值的程度取决于扰动量的大小。总体上，当用水量增加时，液位振荡的中心线幅值低于设定值；当用水量减少时，液位振荡的中心线幅值高于设定值。在扰动消失后，被控量仅需要很短的周期即可跟踪设定值，并且振荡的幅度较小。

6结束语

本文将DMC算法应用于下位系统中，试验证明了算法的有效性。所采用的被控对象符合一般工业控制对象的特性。从试验模型数据看，DMC算法获取数学模型的方式较为简便，且对模型的精度要求不高。系统的动态控制效果优于传统的PID控制。

参考文献

[1] 徐学红,冯冬青.电站锅炉燃烧系统先进控制策略研究[J].自动化仪表,2014,35(2):16-19.

[2] 钱积新,赵均,徐祖华.预测控制[M].北京:化学工业出版社,2007：49-58．

[3] 李俊红,杨马英,穆秀春.基于PLC的大时滞温度对象的动态矩阵控制[J]．浙江工业大学学报,2005,33(1)：56-59．

[4] 张伟伟,余岳峰,罗永浩,等.基于阶跃响应曲线拟合的链条锅炉快速建模方法[J].工业锅炉,2007(2)：1-4．

[5] 杨俊,马姝姝.基于PLC的动态矩阵控制算法实现[J].工业仪表与自动化装置,2008(4)：67-70．

[6] 郭伟,温敬红,周旺平.基于时域的分数阶PID动态矩阵控制算法改进[J].仪器仪表学报,2010,31(5)：968-973．

[7] 邹涛,刘红波,李少远.锅炉汽包水位非自衡系统的预测控制[J].控制理论与应用,2004,21(3)：386-390．

[8] 张喜萍,谭一川,程玉龙.煤矿排水自动控制系统的设计与研究[J].自动化仪表,2013,34(6):45-47.

[9] 廖常初.中型PLC应用教程[M].北京:机械工业出版社,2006:94-105,172-205．

[10]姜建芳.西门子S7-300/400 PLC工程应用技术[M].北京:机械工业出版社,2012:735-790.------------------------------------------------------------------------------------------------

中图分类号：TP273

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201503009

河北省科技厅科技支撑计划基金资助项目(编号：12211602)。

修改稿收到日期：2014-09-10。

第一作者叶昊(1972-)，男，2009年毕业于河北工业大学电子与通信工程专业，获硕士学位，副教授；主要从事过程控制及智能信息处理方面的研究。