自适应粒子群算法在电力经济调度中的应用
Application of Adaptive Particle Swarm Optimization in Power Economic Dispatch
钱景辉 刘小月 杨小健 李荣雨
(南京工业大学电子与信息工程学院,江苏 南京 211816)
(南京工业大学电子与信息工程学院,江苏 南京 211816)
自适应粒子群算法在电力经济调度中的应用
Application of Adaptive Particle Swarm Optimization in Power Economic Dispatch
钱景辉刘小月杨小健李荣雨
(南京工业大学电子与信息工程学院,江苏 南京211816)
(南京工业大学电子与信息工程学院,江苏 南京211816)
摘要:以发电系统中发电费用最低为目标,结合实际发电运行中系统平衡约束和机组操作约束条件,建立了电力经济调度(ED)模型。考虑到标准粒子群(PSO)算法存在收敛速度慢以及早熟收敛的问题,通过引入进化状态估计和精英学习策略,提出一种自适应粒子群优化(APSO)算法,并将其成功应用于求解该ED模型。在Matlab平台对15台机组算例进行了仿真,仿真结果表明自适应粒子群算方法的求解精度更高。
关键词:电力系统自适应粒子群算法经济负荷分配进化状态估计精英学习策略惩罚策略
Abstract:Combining the system equilibrium constraints and unit operating constraints in practical operation, the economic dispatching (ED) model is built with the lowest cost of power generation as the target. Considering the problems existing in particle swarm optimization (PSO), i.e., the slow convergence and premature convergence, through introducing evolutionary state estimation and elite learning strategy, the adaptive particle swarm optimization (APSO) algorithm is proposed and applied successfully in solving the ED model. The simulation is conducted for 15 units under Matlab platform, the results show that the APSO proposed definitely offers high accuracy than PSO.
Keywords:Power systemAdaptive particle swarm optimizationEconomic load dispatchEvolutionary state estimation
Elite learning strategyPenalty strategy
0引言
电力经济调度(economic dispatch,ED)是电力系统规划的基本问题,其求解算法的研究始终是业界的热点问题。近年来,应用于ED问题的求解算法不断涌现。这些算法包括遗传算法[3]、萤火虫算法[4]、微分进化算法[5-6]、蚁群算法等,尤其是粒子群(particle swarm optimization,PSO)算法,取得了一定成效。Ahmed.S等人[7]提出一种基于自适应加速系数的改进PSO算法,Pranava.G等人[8]提出一种采用受限系数的概念来确保粒子收敛性的改进PSO算法,并将这些方法成功应用于ED问题求解。该方法虽然进一步提高了求解速度和精度,但算法求解ED问题时所存在的收敛精度以及局部最优的问题仍需要进一步研究。
本文首先建立了电力经济调度的数学模型,再将进化状态估计和精英学习策略引入到PSO中,提出一种自适应的粒子群优化算法(adaptive particle swarm optimization,APSO),并将其成功应用于ED问题的求解。试验结果表明,该算法提高了求解精度,获得了更好的优化效果。
1电力经济调度的数学模型
1.1 目标函数
经济调度问题是在满足系统平衡条件和机组运行约束条件下,合理分配各机组的负荷,使得系统发电总成本达到最低。该问题属于非线性约束优化问题,其目标函数如下:

(1)
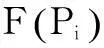
1.2 约束条件
① 系统平衡约束为:

(2)
式中:PD为系统内的总负荷;PS为系统的总网损,其值可采用B系数法计算。
② 机组爬坡约束为:
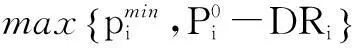
(3)
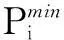
③ 机组出力限制区约束为:
(4)
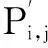
④ 线路容量约束为:
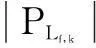
(5)
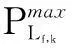
2自适应粒子群优化算法
2.1 粒子群算法
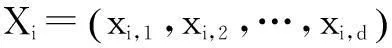
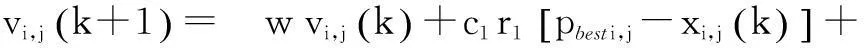
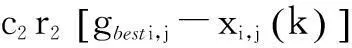
(6)
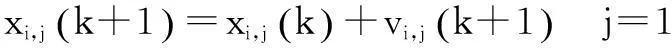
(7)
式中:w为惯性权重;c1、c2为自学习因子;r1、r2为[0,1]区间的随机数。
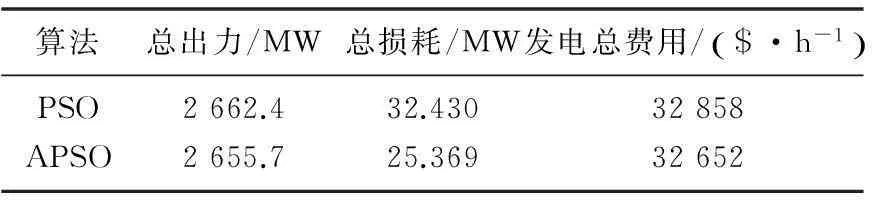
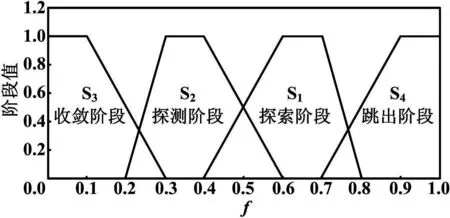
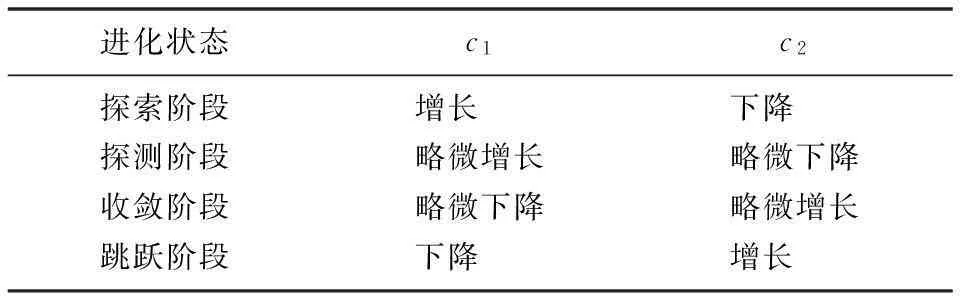
在粒子群算法中,一般会对速度向量vi,j进行最值限制。当vi,j>vmax时,取vi,j=vmax;当vi,j PSO算法具有实现容易、参数设置少等优点,但是作为一种进化计算方法,粒子群算法同样存在收敛速度慢和早熟收敛的问题。本文提出了一种自适应粒子群算法(APSO)[2],通过定义“进化因素”f来定性确定四个进化阶段:探索阶段、探测阶段、收敛阶段以及跳跃阶段。根据不同的进化阶段确定惯性权重w和学习因子c1、c2,当进化阶段处于收敛阶段时,执行精英学习策略,从而避免陷入局部最优。具体步骤如下。 ① 在当前位置下,计算每个粒子i到其他粒子的平均距离: (8) 式中:N为粒子的数目;D为粒子的维度。 ② 计算“进化因素”f: (9) 式中:dg为全局最优粒子到其他粒子的平均距离;dmin、dmax分别为所有距离中的最小值和最大值。 ③ 根据f,采用模糊分类的方式定义四个进化阶段,如图1所示。 图1 四个进化状态分类示意图 ④ 由于较大的w有利于提高算法的全局搜索能力,而较小的w有利于增强算法的局部搜索能力。因此,合理地选取w有利于平衡PSO算法的全局和局部搜索能力。在收敛和探测阶段,需要减小w,从而加强局部搜索能力;而在探索和跳跃阶段,需要增大w,从而提高全局搜索能力。 根据进化状态定义w(f): (10) ⑤ c1和c2决定了粒子本身经验信息和其他粒子的经验信息对粒子运行轨迹的影响,反映了粒子之间的信息交流。设置c1为较大的值,会使粒子更快地到达其自身历史最优位置;而较大的c2值,则又会促使粒子过早收敛到当前的全局最优位置,即容易陷入局部最优。为了有效地控制粒子的飞行速度,使算法达到全局探测和局部开采两者之间的平衡。本文首先初始化c1和c2的值为2,然后再根据进化状态分别调整两者的值,如表1所示。 表1 c1、c2调整策略 ⑥ 由于在粒子群算法中,其他粒子都可以追随个体最优粒子和全局最优粒子来更新自己的位置,而全局最优粒子则没有可追随的粒子,所以在进入收敛阶段时,我们需要引入“精英学习策略”来使全局最优粒子跳出局部最优区域。 (11) 3基于APSO的经济调度求解 由于APSO算法是一种随机算法,因此将该算法应用于ED问题求解时,重点在于等式及不等式约束的处理以及相应的适应函数的构造。 在求解ED问题中,机组爬坡约束、机组出力限制区约束以及线路容量约束均属于不等式约束。为了使每个粒子满足式(3)~式(5)所描述的不等式约束,在通过目标函数评估这些代表发电输出的粒子之前,这些粒子的位置必须在式(3)~式(5)所给出的可行区间之内。 通过限制粒子位置的更新范围,从而确保实际机组负荷符合此类约束条件。 式(2)中的等式约束可以通过在式(1)中加入惩罚函数来处理。 (12) 在受约束的ED问题搜索最优解的过程中,惩罚系数的值会随着迭代次数而增加,从一个较小的初始值增加到一个较大的最终值。这样做的目的是在搜索的早期,使用较小的惩罚值来处理违反等式约束的粒子值,使得这些解有极大可能被保留下来,从而确保粒子的多样性以及算法的全局搜索性。在搜索过程的后期,惩罚系数变大,略微违反等式约束就会产生一个很大的惩罚值,这样就可以保证算法最终尽可能收敛到满足等式约束的解。 APSO算法求解ED问题的具体步骤如下。 ① 输入系统电机组的所有参数,即ED问题中除Pi以外的其他量。 ② 根据系统每个电机组的限制条件以及速度限制条件,初始化符合式(3)~式(5)不等式约束条件的种群中各粒子的速度和位置。 ③ 根据式(12),评价每个粒子的适应度,将当前各粒子到目前为止自己最优的位置和适应值存储在各粒子的pbest中,将所有pbest中适应值最优个体的位置和适应值存储在gbest中。 ④ 根据式(6)、式(7),更新粒子的速度和位置,式(6)中的w、c1、c2根据不同的进化状态进行自适应更改。 ⑤ 如果是在稳定状态下,为避免陷入局部最优,根据式(11)更新gbest值。 ⑥ 若满足停止条件(迭代次数),搜索停止,输出各机组出力值和总发电费用,否则返回步骤③继续搜素。 4算例分析 在由15台机组组成的测试系统中,机组参数如文献[9]所示,种群规模设为100,进化代数设为200代,PSO算法、APSO算法计算各机组总费用出力、总出力、总损耗如表2、表3所示。 表2 15机组系统总费用比较 表3 15机组电力系统出力分配结果 表2和表3表明,APSO算法所得最优解的总出力、总损耗及总费用等指标均优于PSO算法所得最优解,且PSO算法容易陷入局部最优解,而APSO算法能够跳出局部最优解,从而改善了全局搜索能力,提高了结果的精度。 5结束语 本文提出了用于求解ED问题的APSO算法,通过引入合适的惩罚策略来处理电力系统中的平衡约束和机组操作约束条件。APSO算法在PSO算法的基础上,采用进化状态和精英学习策略,从而提高了算法的搜索效率,避免了PSO算法容易陷入局部最优的缺点。 仿真结果验证了基于APSO算法实现的经济调度优化方法在提高结果搜索精度、改善全局搜索能力等方面都起到了较好的作用。 参考文献 [1] Eberhart R,Kennedy J.Particle swarm optimization[J].IEEE International Conference on Neural Networks,1995(4):1942-1948. [2] Zhan Z,Zhang J,Li Y.Adaptive particle swarm optimization[J].IEEE Transactions on Systems Man and Cybernetics,2009,39(7):1362-1381. [3] Chiang C.Improved genetic algorithm for power economic dispatch of units with valve-point effects and multiple fuels[J].IEEE Transactions on Power System,2005,20(4):1690-1699. [4] Yang X,Hosseini S,Gandomi A.Firefly algorithm for solving non-convex economic dispatch problems with valve loading effect[J].Applied Soft Computing,2012,12(5):1180-1186. [5] 刘卓,黄纯,郭振华,等.饱和度自适应微分进化算法在电力经济调度中的应用[J].电网技术,2011,35(1):100-104. [7] Liu Z,Huang C,Guo Z,et al.The application of saturation and adaptive differentialevolution algorithm in economic dispatching ofpowergrid[J].Power System Technology,2011,35(1):100-104. [8] Elsayed S,Sarker R,Essam D.An improved self-adaptivedifferential evolution algorithm for optimization problems industrialinformatics[J].IEEE Transactions on Industrial Information,2013(9):89-99. [9] Ahmed S,Tarek B,Djemai B. Economic dispatch resolution using adaptive acceleration coefficients based PSO considering generator constraints[J].Control,Decision and Information Technologies(CDIT),2013(8):212-217. [10]Pranava G,Prasad P.Constriction coefficient particle swarm optimization for economic load dispatch with valve point loading effects[J].International Conference on Power,Energy and Control(ICPEC),2013(2):350-354. [11]Gaing Z.Particle swarm optimization to solving the economicdispatchdonsidering the generator constraints[J].IEEE Transactions on Power Systems,2003(8):1187-1195.------------------------------------------------------------------------------------------------ 中图分类号:TM731 文献标志码:A DOI:10.16086/j.cnki.issn1000-0380.201503005 修改稿收到日期:2014-08-21。 第一作者钱景辉(1978-),男,2003年毕业于新加坡国立大学计算机科学与技术专业,获硕士学位,讲师;主要从事计算机控制自动化等方面的研究。2.2 自适应粒子群优化算法
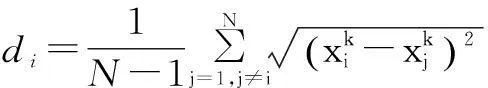

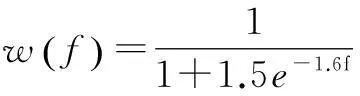
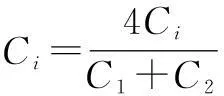
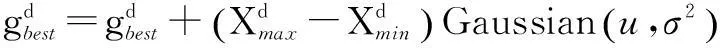
3.1 适应函数构造与约束条件处理
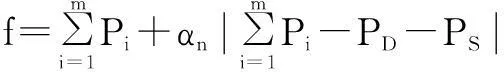
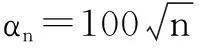

3.2 算法实现的具体步骤