带自适应整定参数的机器人达尔文粒子群优化算法

Robot Darwinian Particle Swarm Optimization

with Self-adaptive Tuning Parameters

余志鹏

(顺德职业技术学院电信系，广东 佛山　528333)

带自适应整定参数的机器人达尔文粒子群优化算法

Robot Darwinian Particle Swarm Optimization

with Self-adaptive Tuning Parameters

余志鹏

(顺德职业技术学院电信系，广东 佛山528333)

摘要：对基数庞大的机器人群族引入达尔文粒子群优化算法(DPSO)。该算法将自然选择应用到粒子群算法中，对整个机器人群族进行动态分割，根据上下文评价指标配合机器人行为对机器人的行为进行预测，提高了机器人群族运动的最优逃脱方案成功率。仿真试验表明，通过对该算法的输入参数进行自适应整定，可以改进系统的收敛率，增加通信的约束，使整个机器人群族在未来更大的范围内有效驱动数量更大的无线机器人群族。

关键词：RDPSO机器人群族上下文评价自适应感知能力

Abstract：The Darwinian particle swarm optimization (DPSO) is introduced in the robots swarm with tremendous cardinality. The algorithm applies natural choice in particle swarm algorithm, dynamically divides the entire robots swarm, and predicts the behavior of robots according to the context evaluation indicator with robot’s behavior, to increase the optimal escape rate of the motion of robots swarm. The simulation tests show that through adaptive tuning of the input parameters of the algorithm, the convergence rate of the system can be improved, the communication constrain is increased, which lead to larger wireless robots swarm can be efficiently driven by entire robots swarm in larger scope in the future.

Keywords：Robot Darwinian particle swarm optimization(RDPSO)Robot swarmContext evaluationSelf-adaptionSensory ability

0引言

在基于群族智能化的仿生算法里，比较著名的是粒子群优化算法(particle swarm optimization，PSO)[1]。PSO包含很多个粒子，这些粒子一起进行空间探索，以找到最优的解决方案。PSO的扩展式(如robotic Darwinian PSO, RDPSO)提出在面对动态和复杂问题时会出现一些障碍，如随时间变化的大量次佳方案问题。通常在自然界中发现的对关联信息缺乏自适应性会作用于次佳方案，可以通过全面的解决方案(如统一机器人的行动)来克服这个缺点[2]。例如，在搜救应用中受难者只要还有一点机会获救，机器人应该坚持搜救。尽管之前提出的RDPSO本来就具备奖惩规则，以激发自然选择来避免停滞，但机器人可能会花费大量时间才意识到它们陷于次优方案或者方案已过时。如对于一个基于嗅觉的群族，因气味受扩散和气流原因影响，所以很难寻找到气味的源头(如对致命气体源的寻找)[3]。对于这些方案，本文将提出几个已有的相关研究。

1相关研究

不考虑PSO的主要变体，解决设定和调整参数的困难，以及在更大范围保持搜索能力的问题，仍然是近来研究工作的重点[4-5]。例如，学界提出的一个最常用的、解决PSO参数设置和调整问题的策略就是基于对该算法的稳定性分析。在文献[5]中，对单个粒子轨迹的广义模型进行分析，广义模型包含了一组系数控制系统的收敛度。经过运算后的系统是一个二阶线性系统，它的稳定性和参数取决于极点的位置，或者状态矩阵的特征值。

Yasuda等人[6]提出一个基于行为的数值稳定性分析算法，包含研究过程中对控制多样化和激烈化的群组行为的反馈。Yasuda等人展示了使用PSO的稳定和非稳定区可控制群组行为。但是，对于分布式的方法，例如RDPSO，在计算群组行为时忽略了一个事实，就是群组里每个机器人不仅需要即时共享它的位置，还需要即时共享它对所有其他成员的相对速度。带有模糊逻辑的合成PSO算法已经完成对这些信息的共享，可以替代上述算法。

模糊逻辑的作用在于不确定性能被包含在决策过程里。模糊和不精确与定性数据的关联衍生出这种逻辑算法，它用语言变量和不确定范围内的重叠关系函数得到结果。例如，在Shi and Eberhart[7]的论文中，把模糊控制与PSO相结合，使系统能动态地自适应粒子惯量。类似地，Liu等人[8]提出一种逻辑控制器，以自适应地调整PSO粒子的最小速率。

目前，没有研究引进自适应行为来克服真实世界情境里的动态特性。机器人的行为需要根据环境的上下文信息来改变。当考虑基于因子、任务相关以及环境情况时[9]，要把上下文知识概念纳入计算中。

2RDPSO算法简介

本节简单地介绍文献[9]提出的RDPSO算法，在文献[10]有进一步的扩展。由于RDPOS算法是在真实移动机器人里对DPSO的改进版，其具有5个特点。①基于分阶数微积分，有更好的惯性影响；②有故障回避动作，避免撞车；③有算法保证MANET协议在整个任务中保持连接；④用异常处理算法对机器人建立二维惯性调度，保护MANET协议的连接，这个算法在机器人里传播得越广越好；⑤用异常赏罚机制来评估机器人的检测和创新效果。

机器人n的行为可以用以下积分方程来描述，在每个离散时间片中，t∈No：

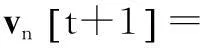
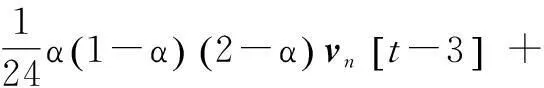
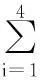
(1)

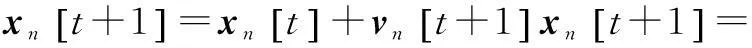
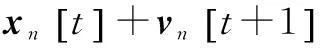
(2)

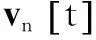
部分系数α允许描述机器人的轨道现象，因为它的内在记忆属性。认知组件χ1[t]和社会组件χ2[t]在PSO算法里是常规的，χ1[t]代表机器人n的局部最佳位置，χ2[t]代表机器人n的全局最佳位置。避障组件χ3[t]由每个机器人的位置代表，它使一个检测距离的障碍的函数g(xn[t])单调递增或递减。在一个没有障碍的环境里，障碍敏感性权重ρ3被设为0。但是，在现实世界中，必须考虑障碍，ρ3的值取决于几个情况：跟主要目标相关(例如，最小消耗功能或最大适应力功能)；跟传感器信息相关(如g(xn[t])的单调性)。MANET组件χ4[t]用最接近的机器人的位置代表，它的位置随着当前机器人位置的最大通信范围dmax增加而增加。更大的ρ4可以提高网络连接，以保证机器人间的特定的范围或者机器人间的信号质量。

除了这些组件，RDPSO用多群族代表，例如，几组机器人一起形成一个群族，各个群族各的行为通过式(1)和式(2)描述。这次方案中，搜索和奖惩规则管理着整个机器人群族，基于“社会排斥”概念(更多细节请查阅[9])。RDOSO奖惩规则如表1所示。

表1　RDPSO奖惩规则

在族群中选取特定的机器人单独考虑，而不是像其他活跃群里的机器人一样寻找目标函数的最优解，因为这样会使机器人随机地游移在场景之中。这样改进算法，使它没那么容易允许目标陷入次优方案之中。存在多个群族允许分布式的方法，因为以往用所有机器人口定义的网络如今被划分成多个更小的网络(每个群族1个)，因此节点减少了，机器人间的信息交换在相同的网络下进行。这就是说，机器人间的相互作用被限制在同一群族内部的相互作用，使得RDPSO的可扩展性可以延伸到大量的机器人。

3自适应系统参数调整

为提高群族里RDPSO机器人的收敛率，机器人应该尽量分散。它们必须保持机器人间最大通信距离或最小信号质量。在此预期下，需要找到加强通信因子ρ4和任务因子(如ρ1和ρ2)的最佳组合，因为机器人通过MANET网络通信的同时要规划自身的路线。

机器人利用之前结果数据最简易的方法是当机器人间的距离接近极限值(如最大距离或最小信号质量)时保证增加通信因子ρ4的权重。因此，探索内部的知识允许定义一个基于因子的上下文标准来表示机器人间的距离。

然而，这种标准需要依靠机器人间最大通信距离dmax或最小信号质量qmin。在现实中，只考虑dmax不能匹配实际的传播模型，因为它更复杂。信号的大小不仅取决于距离，还取决于被其他障碍物反射的多种路径。

这种结构的整体组织与常用的反馈控制器相似，上下文知识是通过对数据的推理分析获得的，再用这些知识控制机器人。因此，基于之前提出和定义的指标，人们可以进入模糊系统工程的输入和输出关系，关系函数会用广义的钟形函数定义。广义钟形函数典型的高斯函数多一个参数，在关系函数里使用的高斯函数的定义为：

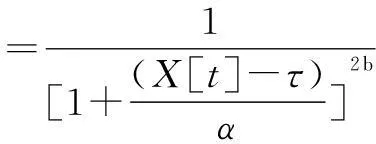
(3)

式中：参数a、b和c各代表曲线的宽度、斜率、中心。

所有的指标都定义为0~1，只有半条曲线被用作代表群族和机器人的状态，如c=1。为了得到更柔和的响应，宽度和斜率可以定义为a=0.5、b=3。

每个输入的一般关系函数如图1所示。

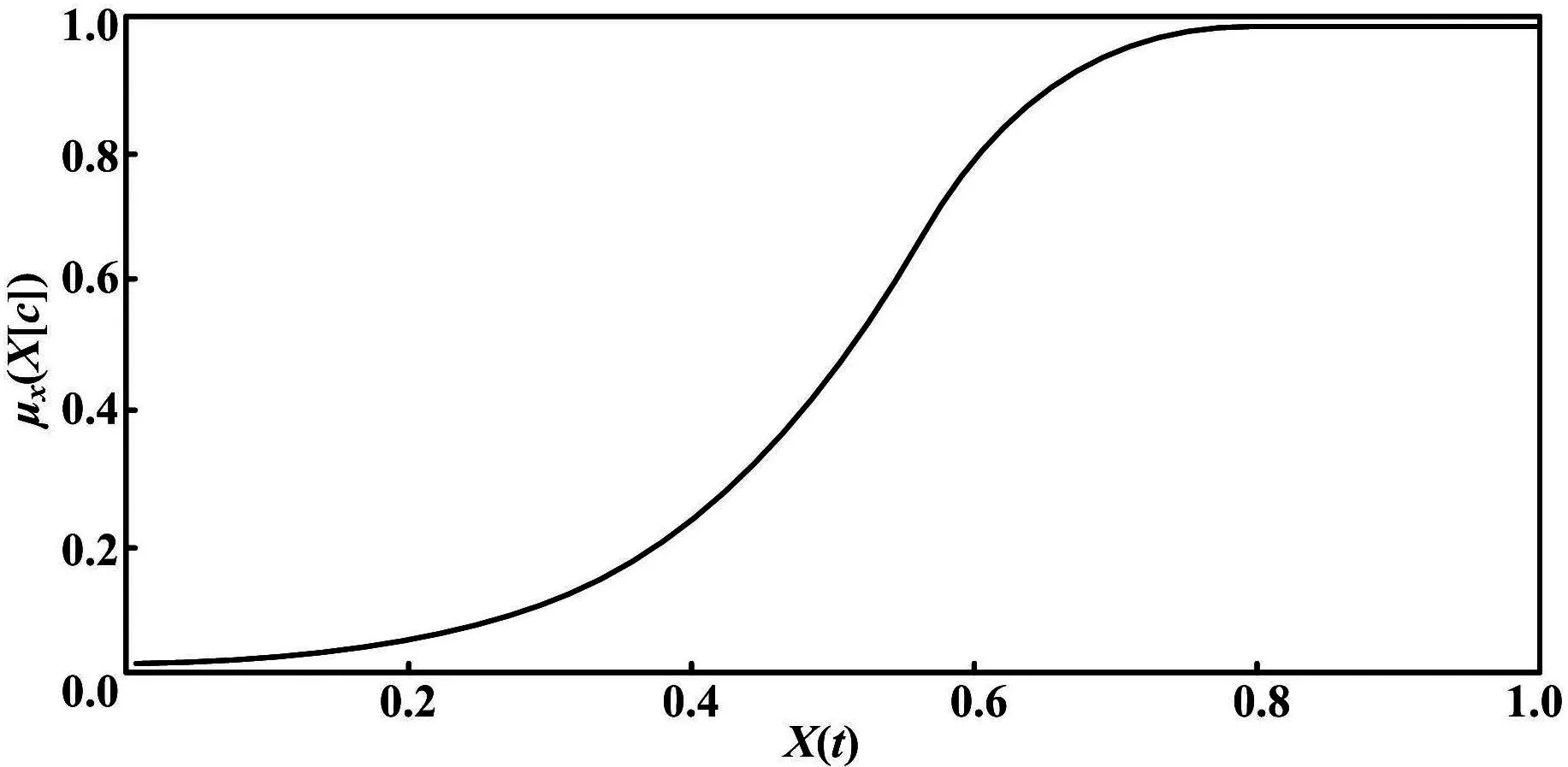
图1　每个输入的一般关系函数

群族动作从属函数μAS(AS[t])代表群族的活跃程度。至于机器人的社会化参数μSn(Sn[t])，它代表机器人的社会化程度。对于避障从属阐述μOn(On[t])，可以作出同样的分析，这里代表了指定机器人里障碍有多远。近似从属函数μPn(Pn[t])代表某个机器人离其邻居的距离。

对于后面的函数，基于对之前部分提出的初步试验评价，定义如图2所示的三角成员关系。这些函数不仅可以软化和表达输出，更重要的一点是还可以把文献[11]所示的吸引因子常规化。

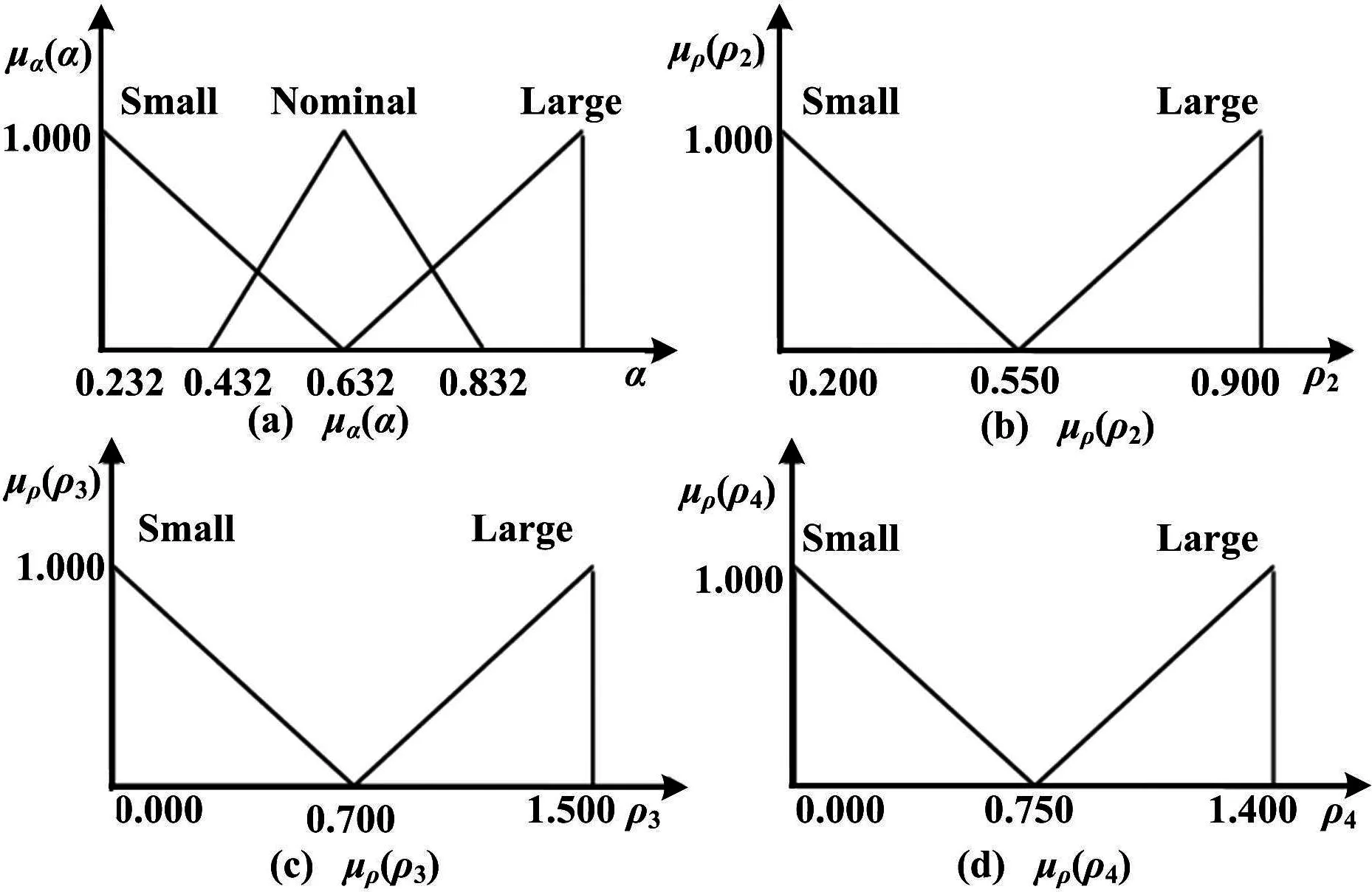
图2　系数量化结果的关系函数

加入模糊系统的目的在于对RDPSO算法可以系统地调整它的行为。通过这种方法，机器人通过观察参数的发展变化，就可以容易地明白关于机器人和群族的上下文信息。因此，上下文知识的使用，通过允许对环境和任务的快速检测，探索真实世界的特性的动态信息，提高了机器人的感知能力(如检测障碍)。

基于用之前定义的指标所代表的输入所提供的信息，模糊逻辑系统可以推论出上下文知识，它可以通过参数的自适应来控制RDPSO的行为。其逻辑推理如图3所示。

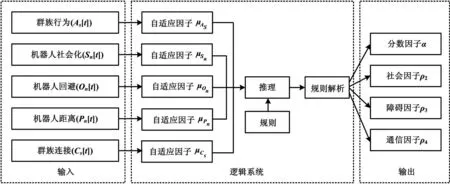
图3　模糊自适应系统控制RDPSO行为逻辑推理图

4仿真试验

本节使用虚拟机器人进行仿真，这样可以对更大数量的机器人在更大的场地里的自适应RDPSO行为进行分析。试验在600 m×600 m模拟场地进行，每次尝试障碍都随机防止。基准方程F(x,y)定义为标准的高斯函数。

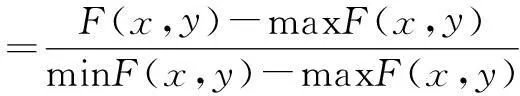
(4)

式中：x-y代表平面坐标，m。

所以，机器人队伍的目标是最大化F (x, y)，也就是最小化原始基准函数F (x, y)，机器人群族要寻找f (x, y)=1的最优方案，而且要避免障碍和保证网络连接。

测试组进行100次测试和500次迭代，每次被设成机器人向量N={50,100,}。然后，一个初始的最小和最大的机器人群族的数量分别为2、5、8。迭代间的最大行走距离被设为0.750 m，也就是max|xn[t+1]-xn[t]|=0.750，机器人间最大通信距离设为dmax=15 m。

图4描述了在50次试验中应用了非自适应和自适应RDPSO算法，计算出的最优方案在中值、首个和第三个四分位数的对于机器人N={50,100}的最终输出。

通过对图4的分析，可以清楚地知道给定的任务可以由任何数量≥25的机器人完成。事实上，除去机器人数量这个因数，大部分情况下，包括非自适应和自适应RDPSO都是收敛的。然而，非自适应算法需要占用首个和1/4中值键间的更大的区域，尤其对于机器人数目巨大的情况。

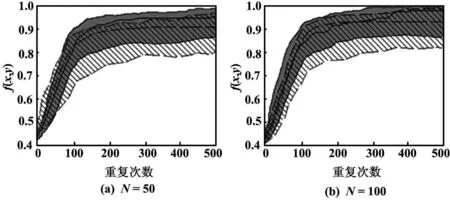
图4　利用非自适应和自适应RDPSO的群族表现

因为环境是连续不断地变化的，对环境的最优方案也是随时间变化的。这要求RDPSO能在短期内找到方案，而且能找到最优方案的轨迹。非自适应算法如常规的RDPSO，在动态环境中通常会出现几个错误，因为它们缺少在动态改变环境中追踪不平稳的最优方案的能力(如文献[12-13])。

函数F(x,y)的动作的A序列如图5所示。

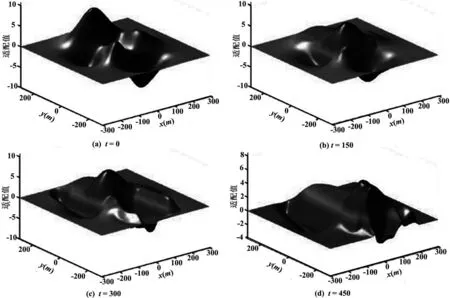
图5　基于强制Duffing振荡器的F(x,y)函数顶峰的平面运动。

混沌函数是最普遍和得到充分研究的方法—产生不稳定函数(如logistic函数[14])。在这篇文献里，采用一种基于强制杜芬振荡器[15]的常规方法动态地改变峰值位置。因此，函数F(x,y)定义为动态时变高斯方程。

每个峰值的动作可以通过元组{γ,ω,ε,Γ,Ω}配置。在元组里，γ控制阻尼的大小，ω控制复原力的大小，ε复原力的非线性量的大小，Γ控制周期驱动力的振幅，Ω控制周期驱动力的频率。尽管为了得到更不可预见的和混沌的行为，元组{γ,ω,ε,Γ,Ω}可能随机定义，为了更好地理解实验结果，他们将被定义为常数{0.1, 1, 0.25, 1, 0.5}。为了使表面平滑，应用一个循环平均过滤器。

5结束语

本文提出RDPSO的延伸算法，具有基于上下文信息的自适应能力。为使算法具有自适应能力，把一个群族置于仿真环境中，以评估机器人障碍与通信等约束下的动态表现。基于上下文的度量被用作模糊系统的输入，系统地适应RDPSO算法。仿真试验结果表明，应用了自适应算法的RDPSO比普通版本的具有更好的收敛性。该算法使用上下文知识，允许对环境和任务的快速检测，探索真实世界的特性的动态信息，提高了机器人的感知能力。即使在动态分布中，自适应RDPSO依然可以比非自适应RDPSO更容易找到最优路径。在日后的工作中，期望在数量更大的机器人群族里使用自适应RDPSO，并将RDPSO与传统类型的机器人群族算法做比对。

参考文献

[1] James K,Russel E.A new optimizer using particle swarm theory[C]//Proceedings of the IEEE Sixth International Symposium on Micro Machine and Human Science,Nagoya,Japan,1995:39-43.

[2] Jim S,Robert M.A survey of animal foraging for directed, persistent search by rescue robotics[C]//Proceedings of the 2011 IEEE International Symposium on Safety,Security and Rescue Robotics,Kyoto,Japan,2011:314-320.

[3] Lino M,Urbano N,Almeida A.Particle swarm-based olfactory guided search Autonomous Robots,2006,20 (3):277-287.

[4] 曾建潮，介婧，崔志华.微粒群算法[M].北京：科学出版社，2004:89-112.

[5] Maurice C,James K.The particle swarm—explosion,stability,and convergence in a multidimensional complex space[J].IEEE Transactions on Evolutionary Computation,2002,6(1):58-73.

[6] Kellchiro Y,Nobuhiro I,Genki U,et al.Particle swarm optimization: a numerical stability analysis and parameter adjustment based on swarm activity[J].IEEJ Transactions on Electrical and Electronic Engineering,2008(3):642-659.

[7] Yuhui Shi,Russel E.Fuzzy adaptive particle swarm optimization[C]//Proceedings of IEEE Computer,2001:101-106.

[8] Liu Hongbo,Abraham A.A fuzzy adaptive turbulent particle swarm optimization[J].International Journal of Innovative Computing and Applications,2007,1(1):39-47.

[9] 张立川，徐德民，刘明雍，等.基于移动长基线的多 AUV协同导航[J].机器人，2009，31(6)：581-585,593.

[10]Micheal S,Couceiro R,Rocha N M.Ferreira.Ensuring Ad Hoc connectivity in distributed search with Robotic Darwinian swarms[C]//Proceedings of the IEEE International Symposium on Safety,Security,and Rescue Robotics,SSRR2011,Kyoto,Japan,2011:284-289.

[11]Micheal S,Couceiro S,Fernando M L.Analysis and parameter adjustment of the RDPSO—towards an understanding of robotic network dynamic partitioning based on Darwin’s theory[J].International Mathematical Forum,2012,7(32)1587-1601.

[12]Aaron C,Gerry D.Adapting particle swarm optimization to dynamic environments[C]//Proceedings of the International Conference on Artificial Intelligence,Las Vegas,USA,2000:429-433.

[13]Xiaohui Cui,Thomas E.Distributed adaptive particle swarm optimizer in dynamic environment[C]//IEEE International Parallel and Distributed Processing Symposium,IPDPS’07,Long Beach,CA,2007: 1-7.

[14]Morrison R,Kenneth A.A test problem generator for non-stationary environments[C]//Proceedings of the 1999 Congress on Evolutionary Computation,CEC’99,Washington DC,USA,1999:786-793.

[15]Chin.A,Kang B.Chaotic motions of a Duffing oscillator subjected to combined parametric and quasiperiodic excitation[J].International Journal of Nonlinear Sciences and Numerical Simulation,2001,2(4):353-364.

中图分类号：TP1

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201503021

修改稿收到日期：2014-06-23。

作者余志鹏(1981-)，男，2007年毕业于华南理工大学控制理论与控制工程专业，获硕士学位，讲师；主要从事机器人控制系统开发的研究。