AIWCS优化SVM在并网逆变器故障诊断中的应用

Application of Optimized SVM and AIWCS in Fault Diagnosis

of Grid-connected Inverter

廖俊勃1　帕孜来·马合木提1　支　婵2

(新疆大学电气工程学院1，新疆 乌鲁木齐　830047;西安工业大学机电工程学院2，陕西 西安　710021)

AIWCS优化SVM在并网逆变器故障诊断中的应用

Application of Optimized SVM and AIWCS in Fault Diagnosis

of Grid-connected Inverter

廖俊勃1帕孜来·马合木提1支婵2

(新疆大学电气工程学院1，新疆 乌鲁木齐830047;西安工业大学机电工程学院2，陕西 西安710021)

摘要：风力发电并网逆变器的故障诊断是确保风电系统运行可靠和安全的关键。支持向量机是故障诊断的一种有效方法。为解决参数选择的不确定性，引入自适应惯性权重布谷鸟(AIWCS)算法来寻求惩罚参数和核函数参数的最优组合，提出基于自适应惯性权重布谷鸟算法优化支持向量机的风力发电并网逆变器故障诊断方法。以三相并网逆变器为例进行仿真试验，对其中电力电子元件IGBT故障进行诊断。仿真结果表明，与遗传-支持向量机和粒子群-支持向量机方法相比，AIWCS具有优化时间短、诊断精度高等特点。

关键词：风力发电并网逆变器自适应惯性权重布谷鸟算法支持向量机故障诊断

Abstract：Fault diagnosis of the grid-connected inverter is the key to ensure the reliability and safety of wind power generation system. Support vector machine (SVM) is an effective method for the fault diagnosis, in order to solve the uncertainty of parameter selection; the adaptive inertia weight cuckoo search (AIWCS) algorithm is introduced to seek out the optimal combination of penalty parameter and kernel function parameter. The fault diagnosis method based on AIWCS algorithm and optimized SVM for grid-connected inverter in wind power generation is proposed. With three-phase grid-connected inverter as example, the simulation experiments are conducted, fault diagnosis of the power electronic device insulated-gate bipolar transistor (IGBT) is implemented. The results show that comparing with genetic algorithm SVM and particle swarm optimization SVM; the AIWCS-SVM possesses shorter optimization time and high diagnostic accuracy.

Keywords：Wind power generationGrid-connected inverterAdaptive inertia weight cuckoo search (AIWCS) algorithm

Support vector machine (SVM)Fault diagnosis

0引言

风力发电并网逆变器是风电系统提供优质电能的重要环节，也是研究的热点问题[1-5]。为了确保风电系统的可靠性和安全性，并网逆变器的故障诊断是十分必要的。

在研究逆变器的故障时，主要是针对逆变器中半导体的故障而讨论,随着研究的不断进行，其故障诊断方法越来越多样化。文献[6]提出了离散傅里叶变换的归一化方法，并与其他故障诊断方法做了对比，解决了动态时误问题，但缺点是只能进行单管故障。文献[7]提出了开关建模方法，该方法诊断时间短，能进行单管和桥壁的开路故障，但需要增加一些电子元件。文献[8]提出了检测各相电流正负半波部分频率方法,对地铁辅助逆变器中单管和双管进行准确的开路故障，但是这种方法只能适用于调制方式的逆变器。

本文应用布谷鸟(cuckoo search，CS)算法,它是模拟某些种类的布谷鸟育雏来有效求解最优化问题的演化算法。该算法简单，参数少，并引入Lévy飞行搜索机制，增加了搜索范围。为了避免CS算法陷入局部最优，提高全局寻优能力和寻优精度，在算法中加入了自适应惯性权重(adaptive inertia weight，AIW)用于对支持向量机(support vector machine,SVM)参数的优化。针对风力发电并网逆变器的故障诊断，提取故障特征向量，并作为诊断方法的输入值，确定输出目标值，然后进行诊断。将本文提出的AIWCS算法与遗传算法(genetic algorithm,GA)、粒子群算法(particle swarm optimization,PSO)进行比较,可以得到AIWCS-SVM算法运行时间更短、诊断精度更高。

1支持向量机

支持向量机(SVM)由Vapnik首先提出[9]，主要思想是建立一个分类超平面作为决策曲面，使得两类之间的隔离边缘被最大化。它避免了人工神经网络等方法的网络结构选择、过学习和欠学习，它可以提供一个在大量训练数据之间只有少数向量的全局优化的分离边界。近几年,支持向量机在工程中得到大量应用[10-12]。

假设样本集T={(xi,yi)|i=1,…,n},其中xi∈Rd，y∈{-1,1}，选用合适的惩罚参数C和核函数,并利用Lagrange优化方法[13]，则有：

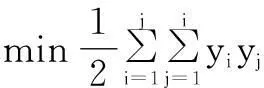
(1)

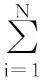
(2)

构造的决策函数为：

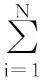
(3)

式中：K(xi,x)为一个进行非线性映射到特征空间的多项式核函数。

核函数有多种类选择[14]：多项式核函数、径向基(RBF)核函数、sigmoid核函数。本文选择径向基核函数：

K(xi,x)=exp(-||x-xi||2/2σ2)

(4)

针对SVM研究，选取径向基核函数是因为径向基核函数局部性较优，不但能实现非线性映射，而且参数少，使其整个模型复杂程度减少。但是对于其中惩罚参数C和径向基核函数中参数σ需要进行选择。本文使用的自适应布谷鸟算法可以自动选择其最佳的参数，使其性能达到最好。

2自适应惯性权重布谷鸟算法

2.1　布谷鸟算法

布谷鸟算法是剑桥大学学者YangXinshe和SDeb在2009年提出的新兴启发算法，是受布谷鸟寻巢孵蛋行为启发而提出的一种新的群智能优化方法[15]。布谷鸟算还结合了Lévy飞行搜索机制[16-17]，将Lévy分布应用其中有利于扩大搜索范围，增加了群多样性。布谷鸟算法具有运算简单、参数少、易于实现等优点。

在CS算法中构造了三条理想化规则。

① 每个布谷鸟一次只孵一个蛋,并放置在一个随机选择的鸟巢中;

② 最优的卵将保留到下一代;

③ 可供选择的鸟巢数量N是固定的,布谷鸟卵被发现的概率为Pa∈[0,1]。

在布谷鸟寻找最优质的鸟巢过程中，位置更新公式为：

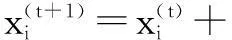
(5)

Lévy(λ)~μ=t-λ1<λ≤3

(6)

根据文献[17]计算Lévy随机数：

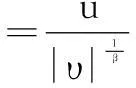
(7)

μ和υ符合正态分布，且：

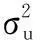
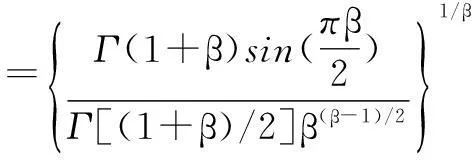
(8)

2.2　自适应惯性权重布谷鸟算法

CS算法被证明其性能接近于标准的粒子群优化算法(PSO)和差分演化算法(differential evolution，DE)[18]。但是和其他智能优化算法一样，CS算法也有后期速度慢、精度不高、局部搜索能力不强等缺点。为了提高全局寻优能力，使CS算法有较好的收敛速度和寻优精度，本文对CS算法进行改进，在算法中加入自适应惯性权重(adaptive inertia weight，AIW)。改进后算法称为自适应惯性权重布谷鸟 (AIWCS) 算法。

在CS算法中，每个鸟窝的位置是随机的，为了获得更大的搜索空间，搜索更多新的区域，本文引入自适应惯性权重ωi，使其在布谷鸟寻找最优质的鸟巢过程中自适应地调节其位置的大小：

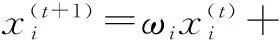
(9)

设群体的惯性权重最小和最大分别为ωmin和ωmax，则当前的自适应惯性权重ωi可以定义[19]为：

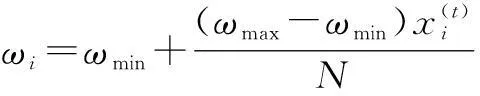
(10)

A1WCS算法增加了自适应惯性权重，当布谷鸟的位置发生变化后，惯性权重也发生了变化，从而调节了全局和局部搜索能力。当CS算法陷入局部最优时，会产生较大的惯性权重，从而使算法跳出局部最优进行全局寻优；当收敛速度较慢时，会产生较小的惯性权重，则有利于局部最优，加速算法收敛。

3基于AIWCS-SVM的故障诊断方法

采用AIWCS算法来优化SVM的的优惩罚参数C和径向基核函数参数σ，寻找两者最优值，确定了AIWCS-SVM模型。AIWCS优化SVM参数的流程图如图1所示。

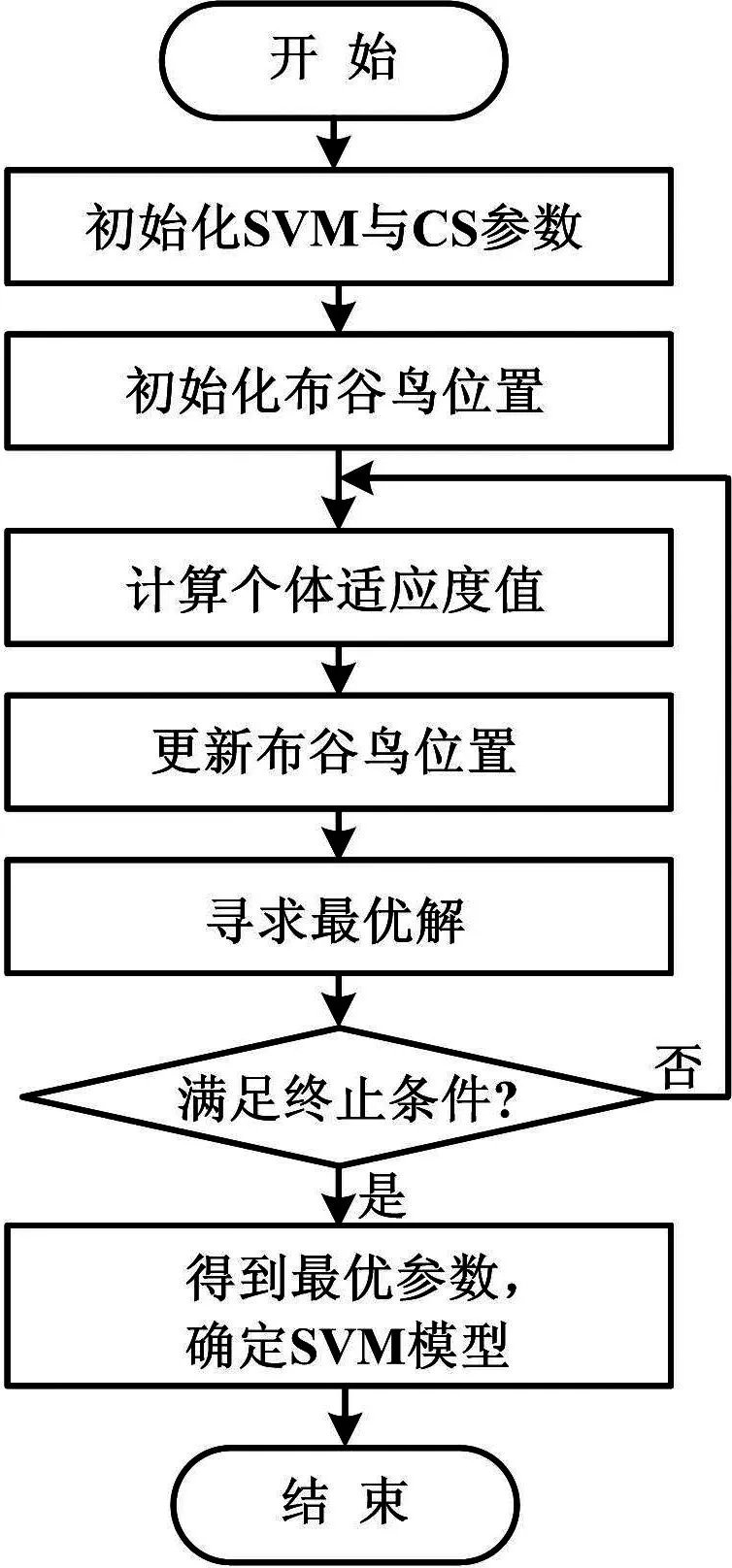
图1　AIWCS优化SVM参数流程图

基于AIWCS-SVM的风力发电并网逆变器故障诊断方法具体步骤如下。

① 对风力发电并网逆变器提取故障特征向量并作为诊断方法的输入值，确定输出目标值。在不同电压下确定训练集和测试集。

② 初始化SVM和CS参数，计算个体的适应度。采用K次交叉验证思想,利用训练数据得到模型，以得到分类准确精度。该精确度定义为个体的适应度。

③ 布谷鸟位置的更新。按式(5)~式(10)，得到新的位置，如果新解优于旧解则替换。以概率Pa进行选择，抛弃差的鸟窝，建立新巢。逐渐迭代寻优，满足条件时记录最优解。

④ 构造AIWCS-SVM诊断模型。由步骤③得到SVM的最优学习参数，确定诊断模型。

⑤ 输入训练数据，对模型进行训练，再输入测试数据，进行预测。

4试验结果分析

以三相并网逆变器为风力发电并网逆变器研究的故障诊断对象，其系统的拓扑结构图如图2所示，其中三相并网逆变器主要由6只IGBT构成(VT1~VT6)。本文探讨的是在IGBT管正常的情况下单管开路和双管开路的22种情况(1种正常情况，6种单管故障和15种双管故障)。对三相并网逆变器的输出电流进行采样(采样频率12 kHz)，建立故障样本时分别选取不同的电压，即选择300 V、500 V为训练样本，350 V、400 V、450 V为测试样本。电网频率不变fs=50 Hz。利用本文提出的AIWCS-SVM算法进行诊断。

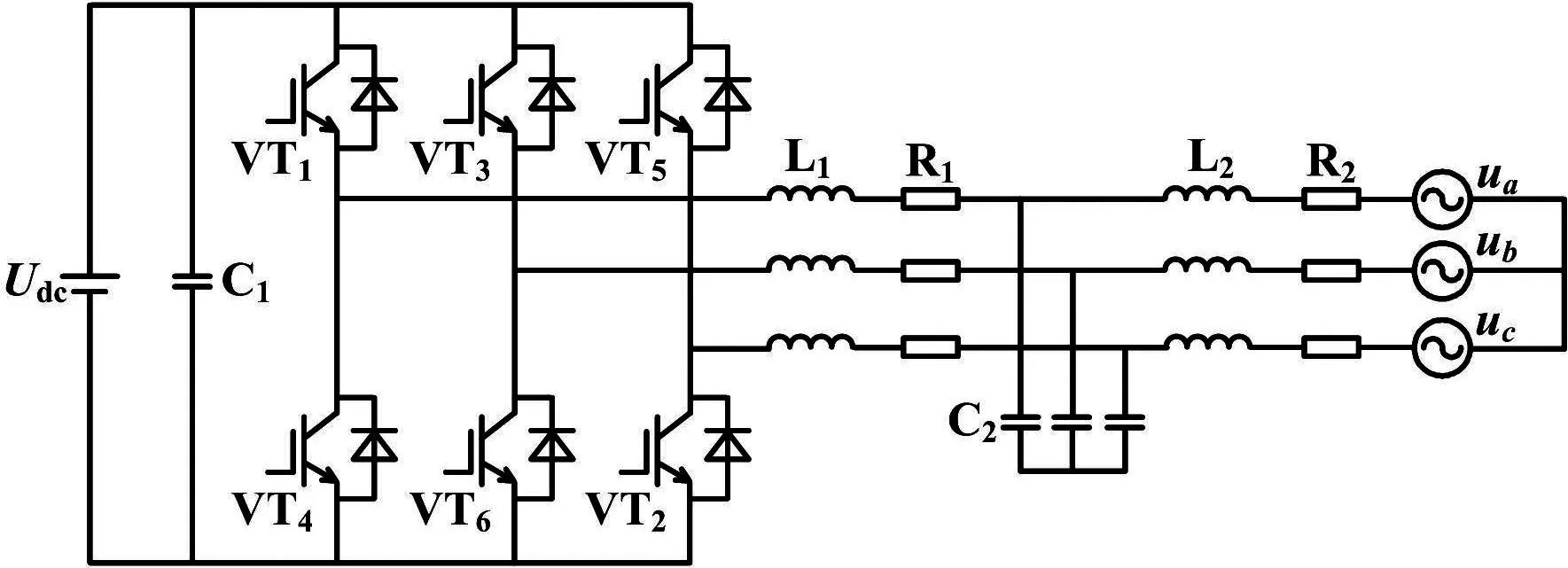
图2　三相并网逆变器拓扑结构图

对电流进行采样之后要转换为需要的信息向量，即故障特征向量。常用的方法有傅里叶变换、功率谱、小波变换等。本文采用小波变换进行信号的分析，用db40小波对采集到的电流信号进行8个尺度的分解。

经过特征提取，得到训练样本和测试样本。表1为部分训练样本，表2为电压为350 V时部分测试数据。其中8个特征值为AIWCS-SVM的输入向量，22种故障类型对应目标输出。

分别采用遗传算法(GA)、粒子群算法(PSO)和AIWCS算法优化SVM的参数，比较其故障诊断效果。设置3种算法的种群规模都为20，迭代次数均为200。其中GA的选择概率为0.9，交叉概率为0.7；PSO的学习因子为1.5，惯性权重为1；AIWCS中惯性因子最大为2，最小为0.5，外来概率为0.25。采用这3种算法优化SVM，得到优化时间和优化后的参数如表3所示。

由表3可以看出，PSO算法的优化时间最长，GA次之，AIWCS算法优化时间最短。相比PSO和GA算法，由于CS算法的运算便捷性，AIWCS算法将近将时间缩短了一半。

自适应的特点提高了CS算法的局部搜索能力，加快了运行速度。根据CS算法的特点，得到的参数偏小，并且C与σ值相等。因此，AIWCS算法在寻优能力、运行速度等方面都比GA算法和PSO算法强，能为SVM的模型提供更好的参数。

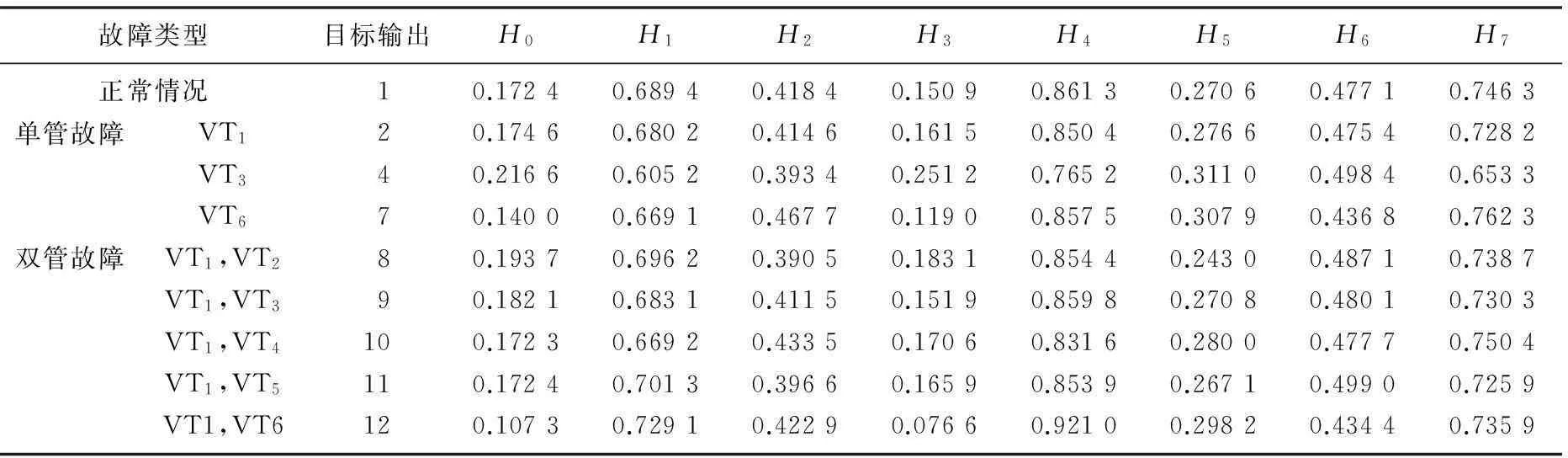
表2　350 V的部分测试样本

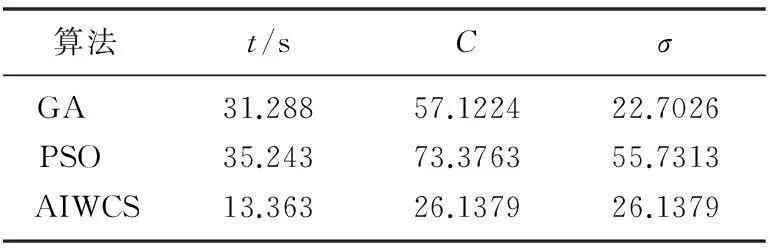
表3　3种算法优化时间和优化后的参数

利用算法对SVM参数寻优，将得到的结果代入到SVM中，即为AIWCS-SVM模型。利用A1WCS-SVM、GA-SVM和PSO-SVM算法对测试样本进行诊断，得到的诊断结果如表4所示。

通过验证可以看出，AIWCS-SVM的平均误差为1.01%，整体故障诊断精度为96.969 7%。GA-SVM的平均误差为2.53%，整体故障诊断精度为92.424 2%。PSO-SVM的平均误差为2.02%，整体故障诊断精度为93.939 4%。由此可知本文提出的AIWCS算法优化SVM方法对于风力发电并网逆变器的故障诊断有很高的精度。

表4　故障程度诊断结果

5结束语

本文提出将自适应惯性权重布谷鸟算法应用于支持向量机中，以寻找最优参数。将这种方法用于风力发电并网逆变器的故障诊断，结果表明了AIWCS-SVM算法对三相并网逆变器的故障诊断的正确性和可行性。AIWCS算法不但能够调节全局和局部搜索能力，而且避免其陷入局部最优值。AIWCS算法优化SVM参数，优化时间短，优化后得到的AIWCS-SVM诊断精度高。与GA-SVM和PSO-SVM算法相比，A1WCS算法具有更短的寻优时间和更高的诊断精度，应用前景好。

参考文献

[1] Liserre M,Teodorescu R,Blaabjerg F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].Power Electronics,IEEE Transactions on,2006,21(1):263-272.

[2] Kim H,Yu T,Choi S.Indirect current control algorithm for utility interactive inverters in distributed generation systems[J].Power Electronics,IEEE Transactions on,2008,23(3):1342-1347.

[3] 张强,张崇巍,张兴，等.风力发电用大功率并网逆变器研究[J].中国电机工程学报,2007,27(16):54-59.

[4] 黄曌,易灵芝,彭寒梅，等.基于SVPWM过调制策略的SRG 风力发电系统并网逆变器[J].电力自动化设备,2010,30(10):89-93,97

[5] 陈增禄,班培刚,史强强.抑制并网逆变器电流谐波的带通调节器研究[J].电网技术,2013,37(6):1706-1712.

[6] 于泳,蒋生成,杨荣峰，等.变频器 IGBT 开路故障诊断方法[J].中国电机工程学报,2011,31(9)：30-35．

[7] 安群涛,孙力,赵克，等.基于开关函数模型的逆变器开路故障诊断方法[J].中国电机工程学报，2010,30(6)：1-6．

[8] 赏吴俊,何正友,胡海涛，等.基于IGBT输出功率的逆变器开路故障诊断方法[J].电网技术,2013,37(4): 1140-1145.

[9] Cortes C,Vapnik V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.

[10]凌武能,杭乃善,李如琦.基于云支持向量机模型的短期风电功率预测[J].电力自动化设备,2013,33(7):34-38.

[11]陈华丰,张葛祥.基于决策树和支持向量机的电能质量扰动识别[J].电网技术,2013,37(5):1272-1278.

[12]汤昶烽,卫志农,李志杰，等.基于因子分析和支持向量机的电网故障风险评估[J].电网技术,2013,37(4):1039-1044.

[13]Sebald D J,Bucklew J A.Support vector machine techniques for nonlinear equalization[J].Signal Processing,IEEE Transactions on,2000,48(11):3217-3226.

[14]纪昌明,周婷,向腾飞，等.基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用[J].电力自动化设备,2014,34(3):125-129,131.

[15]Yang X S,Deb S.Cuckoo search via Lévy flights[C]//Nature & Biologically Inspired Computing,World Congress on.IEEE,2009:210-214.

[16]Barthelemy P,Bertolotti J,Wiersma D S.A Lévy flight for light[J].Nature,2008,453(7194):495-498.

[17]Yang X S. Nature-inspired metaheuristic algorithms[M].Luniver Press,2010.

[18]Civicioglu P,Besdok E.A conceptual comparison of the Cuckoo-search,particle swarm optimization, differential evolution and artificial bee colony algorithms[J].Artificial Intelligence Review,2013,39(4):315-346.

[19]Panigrahi B K,Ravikumar V,Das S.Adaptive particle swarm optimization approach for static and dynamic economic load dispatch[J].Energy Conversion and Management,2008,49(6):1407-1415.

中图分类号：TM464

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201503004

国家自然科学基金资助项目(编号：61364010)。

修改稿收到日期：2014-08-24。

第一作者廖俊勃(1987-)，男，现为新疆大学控制科学与工程专业在读硕士研究生；主要从事过程检测、诊断与控制技术(含风力发电)的研究。