基于降维四元旋转不变子空间算法的波达角估计

赵继超 陶海红 高志奇

（西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安710071）

引 言

由同点配置的二维矢量天线组成的极化敏感传感器阵列在对极化信号进行波达角（Direction of Arrival，DOA）估计时，传统做法是将各个相互正交的天线分量的接收数据按照阵列空间维数排列展开，形成一个长的数据矢量，即长矢量（Long Vector，LV）数据模型.这种模型忽略了天线分量间的正交关系，针对长矢量模型的不足，国内外学者将极化敏感阵列接收数据模型从复数域拓展为超复数域，开始研究四元数模型下极化敏感传感器阵列的参数估计.

四元数模型相较于复数模型多了两个虚部，使得四元数模型能更好地表征极化敏感阵列接收数据的正交性.文献［1］详细阐述了四元数的基本运算以及四元数矩阵奇异值分解（Singular Value Decomposition，SVD）的实现，为四元数模型在极化敏感阵列信号处理中的应用奠定了数学基础.由于多重信号分类（Multiple Signal Classification，MUSIC）算法是基于信号子空间和噪声子空间正交性实现超分辨DOA估计，而四元数模型相比复数模型包含了更多的数据正交信息，所以Sebastian Miron等学者于2006年在文献［2］中首次提出了基于二分量极化敏感阵列，四元数模型下的MUSIC（Quaternion MUSIC，Q-MUSIC），仿真结果充分地说明了四元数模型在极化敏感阵列信号处理中的优势，文献［3］又针对六分量全电磁矢量传感器，将四元数扩展到双四元数，提出了双四元数模型下的MUSIC（Biquaternions MUSIC，BQ-MUSIC）算法，文献［4］又在双四元数的基础上，将四四元数模型应用在全电磁矢量阵列DOA估计中，提出了四四元数MUSIC（Quad-quaternion MUSIC，QQ-MUSIC）算法，但是上述三种算法均需要四维谱峰搜索，运算量十分巨大，实时性差，不适用于实际场合应用.陶建武等人［5-7］在极化敏感阵列参数估计方面做了很多的研究，针对四元数模型下四维谱峰搜索运算量大的问题，在文献［6-7］中提出了降维Q-MUSIC算法，将四维谱峰搜索降低为两次二维谱峰搜索，有效地降低了运算量.文献［8］提出了由二维矢量天线组成的均匀线阵（Uniform Linear Array，ULA）的长矢量旋转不变子空间算法（Long Vector Estimation of Signal Parameters via Rotational Invariance Techniques，LV-ESPRIT），文献［9］在文献［8］的研究基础上加入了四元数模型，提出了四元数ESPRIT（Quaternion ESPRIT，Q-ESPRIT）算法，无需谱峰搜索就可以实现DOA和极化信息的估计，但是该算法和文献［7］所提算法存在同样的问题，需要提前已知入射信号的方位角或者俯仰角，否则无法构造极化域的旋转不变性估计信号极化信息.文献［6-9］都是基于传统同点配置的二维矢量天线组成的ULA，在四元数模型下，利用Q-MUSIC和QESPRIT在求解接收数据的协方差矩阵时，均会出现“四元数模型相干”问题，该问题在文章的第2部分会细述，这将导致四元数正交信息的丢失，以及信号极化信息的估计失败，文献［7］虽然发现了该问题，但是却没有提出该问题的有效解决方法，而是通过传统长矢量方法去估计信号的极化信息.

本文选取的极化敏感阵列是在由共点配置正交小磁环-短偶极子（Co-centered Orthogonal Loop and Dipole，COLD）天线组成的ULA的基础上，添置一个严格指向z轴的短偶极子天线，采用新增天线接收数据与原始ULA接收数据的互相关矩阵代替传统的ULA接收数据协方差矩阵，有效地解决了“四元数模型相干”问题，却同时损失了信源数减一个阵列的孔径信息，孔径损失问题在文章第3部分具体讲述，由于新算法充分利用了四元数模型的正交信息和四元数的结构特点，不仅提高了估计精度，而且实现了无需已知信号的方位角或者俯仰角，仅通过一次特征值分解（Eigenvalue Decomposition，EVD）就能够估计入射信号的DOA和极化信息，运算量更低.

符号定义：Η，C和R分别表示四元数域，复数域和实数域；（·）†，（·）-1，（·）H和（·）＊分别表示广义逆，矩阵求逆，共轭转置和共轭运算；表示Α的估计值；arg（·）表示取角度运算；Re（·），（·）i，（·）j和（·）k分别表示取四元数的实部，i部，j部和k部.

1 四元数及相关运算

四元数是由Hamilton于1843年提出的一种四维超复数，四元数h由一个实部和三个虚部组成：h＝a＋bi＋cj＋dk，其中a，b，c，d∈R，虚部i，j，k满足：

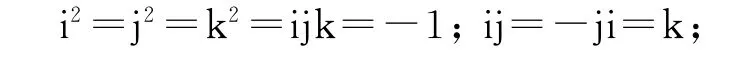
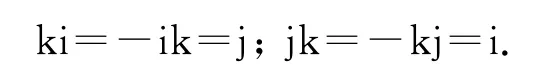
简要介绍下本文用到的四元数基本运算，定义四元数h的共轭h＊为h＊＝a-bi-cj-dk.

设两个四元数h1和h2分别为h1＝a1＋b1i＋c1j＋d1k和h2＝a2＋b2i＋c2j＋d2k，两个四元数相乘取共轭可以表示为（h1h2）＊＝；特别注意的是四元数的乘法不满足乘法交换律：h1·h2≠h2·h1；四元数的除法也不满足交换律：h1h2／h2＝h1，h1h2／h1≠h2.

2 四元数模型相干问题

假设有M个彼此独立的远场窄带完全极化信号，极化敏感阵列是由N个COLD天线组成的ULA，短偶极子严格指向x轴，小磁环的法线严格指向z轴，如图1所示.

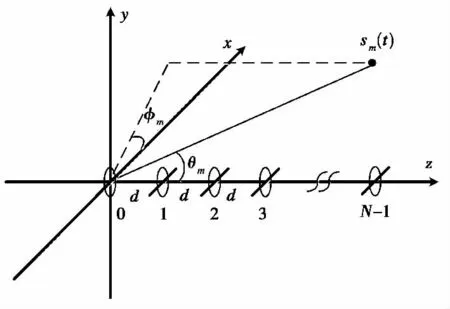
图1 传统COLD组成的ULA

在四元数模型下，极化敏感阵列接收数据矩阵可以表示为

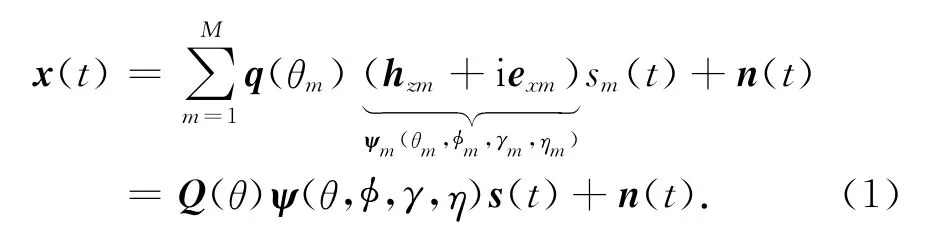
式 中：接 收 数 据 矩 阵x（t）＝［x1（t），x2（t），…，xN（t）］T，x（t）∈H；阵元空间相移矩阵Q（θ，φ）＝［q（θ1，φ1），…，q（θM，φM）］，q（θm，φm）＝［1，ejβm，ej2βm，…，ej（N-1）βm］T为第m个信号的阵元空间相移矢量，是入射信源的波长，阵元间距d＝λ／2；极化-角度域导向矩阵ψ＝diag｛ψ1，…，ψM｝，ψm＝hzm＋i exm为第m个信号的极化-角度域导向矢量四元数表示，exm＝cos φmcosθmsinγmejηm-sinφmcosγm，hzm＝sinθmcos γm，其中，φm∈［0，2π）、θm∈［0，π］、γm∈［0，π／2］、ηm＝［-π，π）分别是第m个信号的方位角、俯仰角、极化 辅 角 和 极 化 相 位 差［10］；s（t）＝［s1（t），…，sM（t）］T为信号矢量；n（t）＝nz（t）＋i nx（t）表示四元数模型下空间加性高斯白噪声，假设矢量传感器接收的每个噪声分量彼此独立且功率均为σ2.

在四元数模型下，极化敏感阵列接收数据的协方差矩阵为

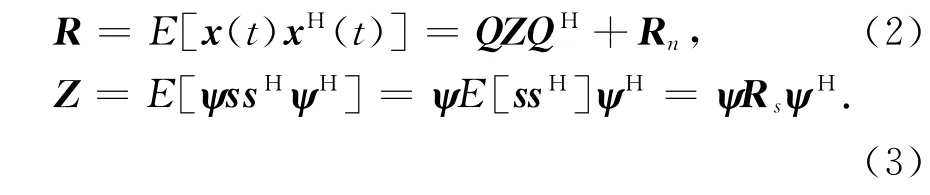
噪声矢量协方差矩阵Rn＝2σ2I，假设信号为彼此独立的远场窄带完全极化信号，信号矢量协方差矩阵Rs是一个实对角矩阵，即Rs＝diag｛ps1，ps2，…，psM｝，对角线元素表征了入射信号的功率，则Z可以表示成

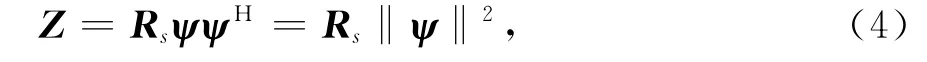
式中‖ψ‖2＝diag｛｜ψ1｜2，…，｜ψM｜2｝.Z为一个实对角矩阵，即接收数据的协方差矩阵R∈C，在四元数模型下，第m个信号的极化-角度域导向矢量ψm＝hzm＋i exm，实部和虚部i表征了空间彼此正交的小磁环和偶极子天线接收数据的方向信息，但是经过自相关运算后只剩下模值信息，用四元数的实部和虚部表征的方向信息已经丢失，本文将这种接收数据x（t）∈H的协方差矩阵R∈C，丢失了四元数模型正交信息的情况称为“四元数模型相干”问题.

对式（1）进行简单的分析，便可以清楚地得知同点配置正交小磁环-短偶极子二维矢量天线组成的均匀线阵出现“四元数模型相干”的原因：由于正交小磁环-短偶极子二维矢量天线是空间共几何中心分布的，使得信号的极化-角度域导向矢量类似于是空间相位因子的公共系数，使得在求解接收数据协方差矩阵时只能得到极化-角度域导向矢量的模值，没有充分利用四元数的正交方向信息；另一方面，极化-角度域导向矢量的模值在接收数据协方差矩阵中可以当作是入射信号的幅度信息，这将直接导致对接收数据的协方差矩阵做特征分解时，极化信息被包含在特征值中，特征向量不包含极化信息，因此目前基于共点配置的二分量极化敏感阵列的Q-MUSIC算法都是降维MUSIC算法，而Q-ESPRIT算法也只能估计出信号的波达角，而信号的极化信息需要借助传统的“长矢量”方法重新估计，李京书，陶建武在文献［7］的仿真实验也指出了该问题，但是却没有提出解决的办法.

3 基于互相关矩阵降维Q-ESPRIT算法的DOA估计

为了解决“四元数模型相干”问题，本文在原来的极化敏感阵列的基础上添置一个严格指向z轴的短偶极子天线，如图2所示.

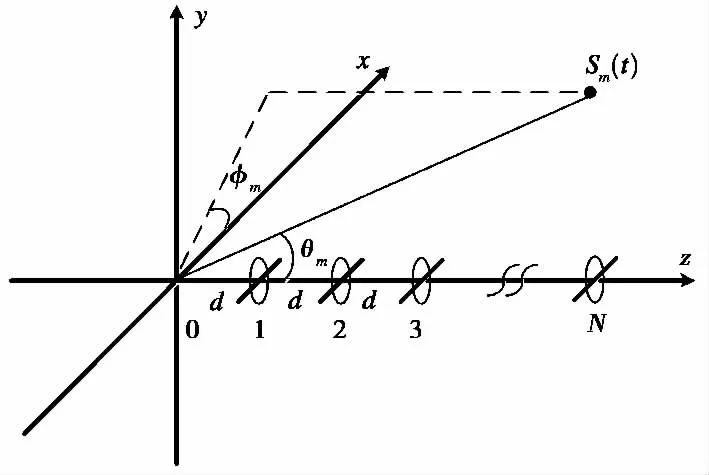
图2 本文所提阵列

将新增严格指向z轴的短偶极子天线当作参考原点，在四元数模型下，新极化敏感阵列的接收数据为：

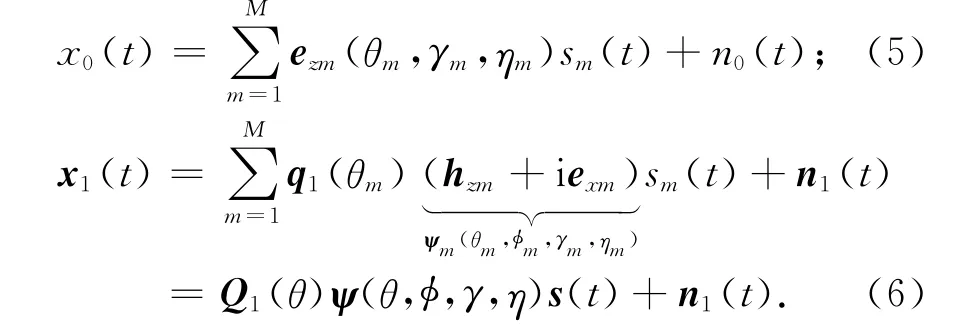
式中：x0（t）表示作为参考点处严格指向z轴的短偶极子天线接收的数据；第m个信号的极化-角度域导向矢量exm（θm，γm，ηm）＝-sinθmsinγmejηm，m＝1，2，…，M；n0（t）为参考原点处短偶极子接收的噪声分量；COLD阵列接收数据矩阵x1（t）的表达形式与式（1）基本一致，唯独由于参考点的不同，阵元空间相移矩阵稍微有所不同，Q1（θ，φ）＝［q1（θ1，φ1），…，q1（θM，φM）］，其 中q1（θm）＝ ［ejβm，ej2βm，…，ejNβm］T为第m个信号的阵元空间相移矢量，同样假设矢量传感器接收的每个噪声分量彼此独立且功率均为σ2.

采用求解x0（t）和x1（t）的互相关矩阵来避免“四元数模型相干”问题，互相关矩阵的另外一个优势是因为假设矢量传感器接收的每个噪声分量彼此独立，互相关运算能有效降低噪声对角度估计精度的影响.x0（t）和x1（t）互相关矩阵可以表示为

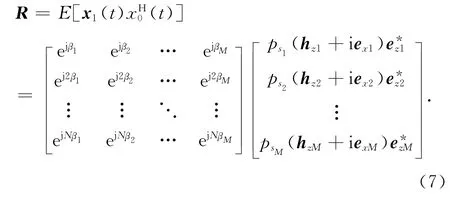
从式（7）可以看出，N×1维的互相关矩阵R包含了入射信号的波达角和极化角信息，类似于参考文献［11］的平滑思想，构造（N＋1-M）×M维矩阵Rα

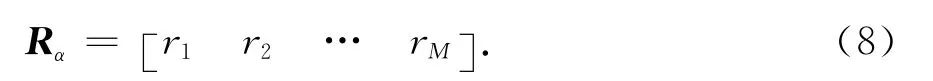
式中，矩阵Rα的第m列rm＝R（m：N-M＋m），m＝1，2，…，M，R（p：q）表示由互相关矩阵R的第p行到第q行组成的列矢量，假设信源数已知或者已经由信源数估计算法估计得出.

结合式（7）和式（8），Rα可以表示成

式中，Υm＝psm（hzm＋i exm，m＝1，2，…，M.为了表述方便，记

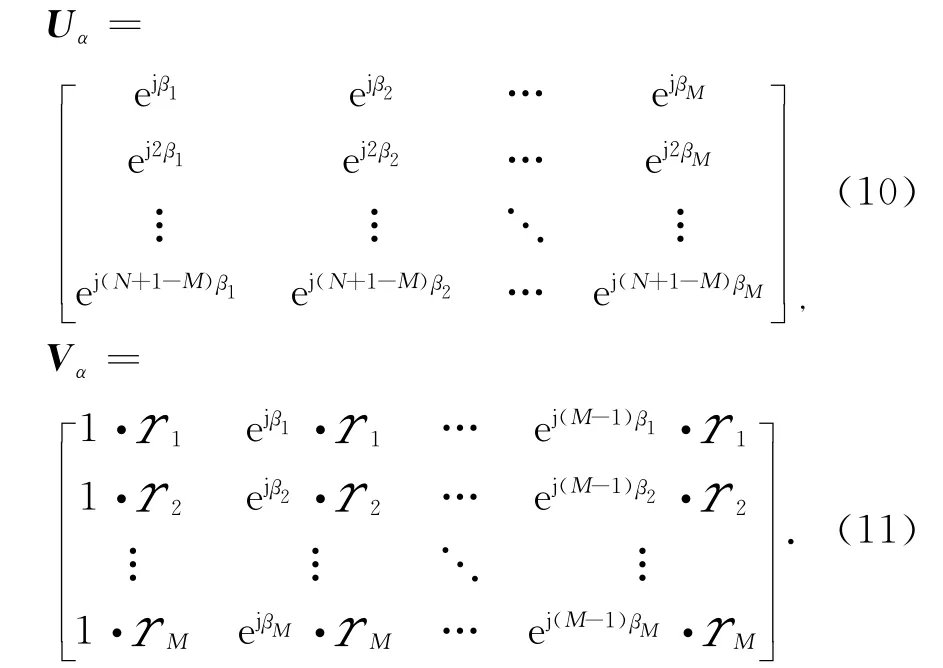
其中，Uα和Vα是两个具有范德蒙结构的矩阵，由于假设入射信号是彼此独立的远场窄带完全极化信号，因此，Uα和Rα张成的空间一样，且Uα和Rα的秩均为信源数目M.

定 义 选 择 矩 阵J1＝［IN-M，01］，J2＝［01，IN-M］，其中，IN-M是（N-M）×（N-M）维单位矩阵，01是（N-M）×1的全零列向量，则有：

式中：Rα1是由Rα的第1行至N-M行组成的矩阵；Rα2为Rα的第2行至N-M＋1行组成的矩阵.由式（9）可以得出Rα1和Rα2存在旋转不变结构：

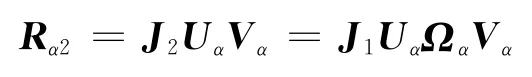
式 中，旋 转 矩 阵Ωα＝diag｛ejβ1，ejβ2，…，ejβM｝.由ESPRIT算法可知：旋转矩阵Ωα可以通过特征分解矩阵得到的特征值进行估计，Vα由特征值对应的特征向量组成的矩阵进行估计，即

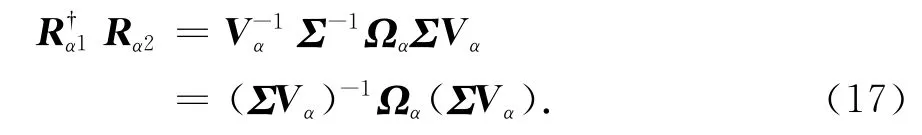
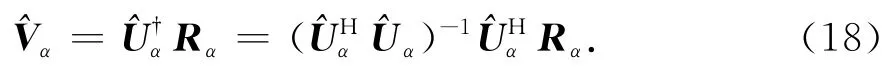
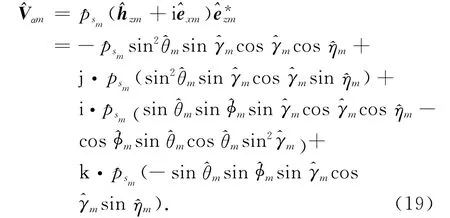
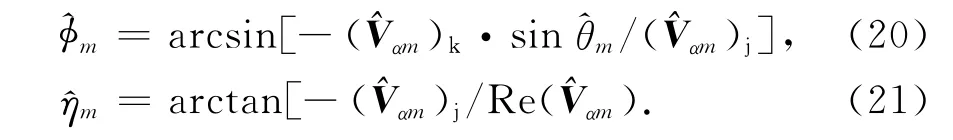
入射信号的俯仰角、方位角和极化相位差已经分别由式（16）、式（20）和式（21）估计出，则入射信号的极化辅角可以由下式估计

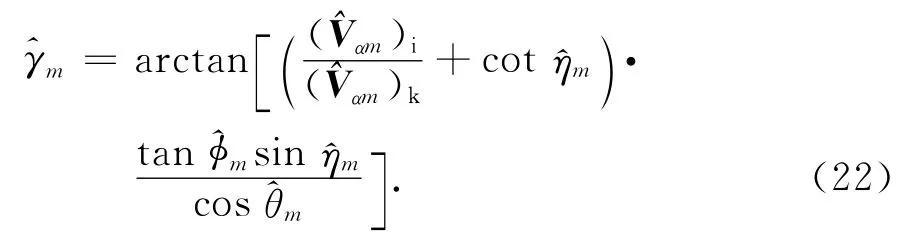
4 所提算法总结及计算量分析

假设两个实数相加计一次加法，相乘计一次乘法，则两个复数相加算2次加法，相乘算2次加法和4次乘法；复数和四元数相加算2次加法，相乘算4次加法和8次乘法；两个四元数相加算4次加法，相乘算12次加法和16次乘法.由于乘法运算的资源耗费是加法的4～6倍，所以本文只分析数乘运算量.假设信源数为M，COLD组成的ULA阵元数为N，快拍数为L，下面给出本文所提算法的步骤，及其每步的运算量：1）求解互相关矩阵R＝E［x1（t）（t）］，运算量为16 NL；2）构造Rα1和Rα2，并求解矩阵，运算量为ο（（4 M）3）；3）EVD分解，运算量为ο（（4 M）3）；4）估计俯仰角，运算量为4 M；5）估计矩阵，运算量为NM＋MM2；6）估计矩阵，运算量为ο（（4 M）3）；7）估计方位角，运算量为2 M；8）估计极化相位差，运算量为M；9）估计极化辅角，运算量为4 M.

文献［9］的传统Q-ESPRIT需要通过两次EVD分解，即基于四元数EVD分解估计信号的波达角，基于长矢量模型EVD分解估计信号的极化信息，而本文只需一次四元数EVD分解，降低了运算量，实时性得到了提高，且本文算法充分利用了四元数模型的正交信息和数据结构特征，可以直接估计出信号的DOA和极化信息，无需像文献［8-9］需要提前已知入射信号的方位角或者俯仰角.

5 仿真实验

在仿真实验部分，给出了一些仿真结果来说明所提算法的性能，并与文献［8］的LV-ESPRIT和文献［9］的Q-ESPRIT进行了对比.

实验1 假设COLD天线数目为5，入射信源数为2，信号的俯仰角、方位角、极化辅角和极化相位差分别为：θ1＝50°，φ1＝40°，γ1＝60°，η1＝45°；θ2＝40°，φ2＝30°，γ2＝70°，η2＝55°，阵间距理想的认为等于半波长，由于LV-ESPRIT和Q-ESPRIT算法需要入射信号方位角或者俯仰角先验信息，所以对该两种传统算法进行仿真时假设方位角已知，而本文算法无需任何入射角的先验信息就可以估计出入射信号的DOA和极化信息.图3为在小快拍和大快拍两种条件下，本文算法、LV-ESPRIT和QESPRIT算法估计的俯仰角和极化信息标准误差随信噪比的变化曲线；图4为在低信噪比和高信噪比两种条件下，本文算法、LV-ESPRIT和Q-ESPRIT算法估计的俯仰角和极化信息标准误差随快拍数的变化曲线；方位角因为没有对比参照，所以图5给出了本文算法估计得到的方位角和俯仰角散布图，执行500次独立的蒙特卡洛实验.

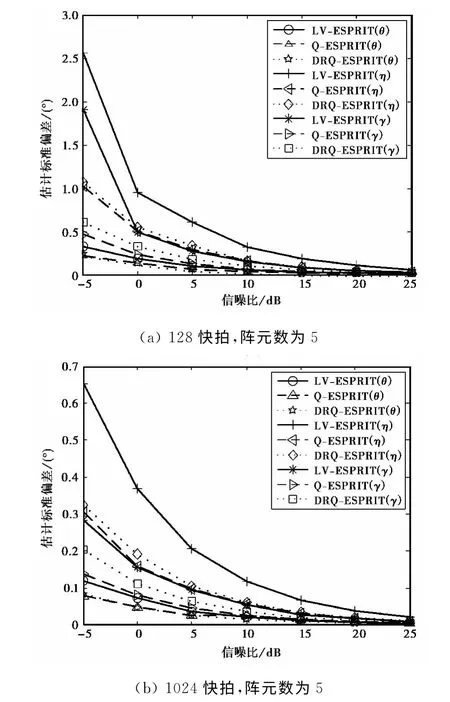
图3 估计标准偏差随信噪比的变化曲线

由图3和图4可以得出：1）基于四元数模型的两种算法，估计精度明显高于基于复数模型的算法，这是由于四元数模型比复数模型包含了更多的数据正交信息，说明了四元数模型优于复数模型；2）本文算法的估计精度略逊色于传统Q-ESPRIT算法，主要有两个原因，其一是仿真传统Q-ESPRIT时，假设方位角已知，模型简化引起使传统算法误差的降低，其二是由于本文算法损失了部分孔径信息.由图5可以得出：1）本文算法可以估计出入射信号的方位角，无需任何先验信息；2）在低信噪比、小快拍条件下，方位角的估计误差明显高于俯仰角的估计误差，这是由于本文算法是基于式（22）和式（23），通过俯仰角的估计值实现方位角的估计，这会造成俯仰角估计误差积累，导致方位角的估计精度低于俯仰角.

实验2 由文章的第4部分可知，实验1中本文算法的有效孔径数目仅为4个COLD天线，所以实验2假设LV-ESPRIT和Q-ESPRIT算法的阵元数为4个COLD天线，本文算法的阵元数依然为5个COLD阵，对比在有效孔径相同的条件下，本文算法与LV-ESPRIT和Q-ESPRIT的性能.图6为在小快拍和大快拍两种条件下，本文算法、LV-ESPRIT和Q-ESPRIT估计的俯仰角和极化信息标准误差随信噪比的变化曲线；图7为在低信噪比和高信噪比两种条件下，本文算法、LV-ESPRIT和QESPRIT算法估计的俯仰角和极化信息标准误差随快拍数的变化曲线.

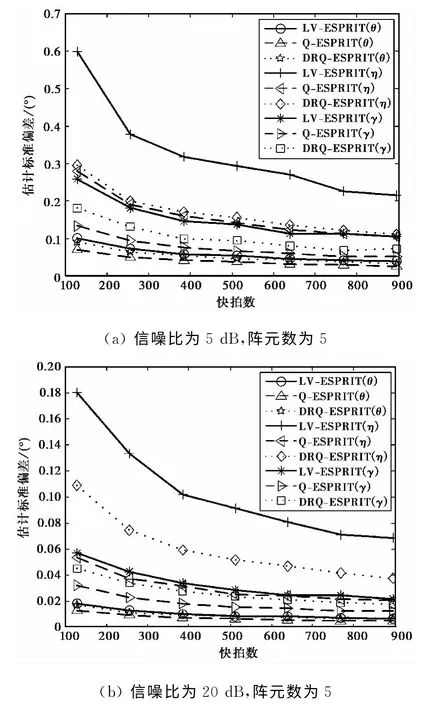
图4 估计标准偏差随快拍数的变化曲线

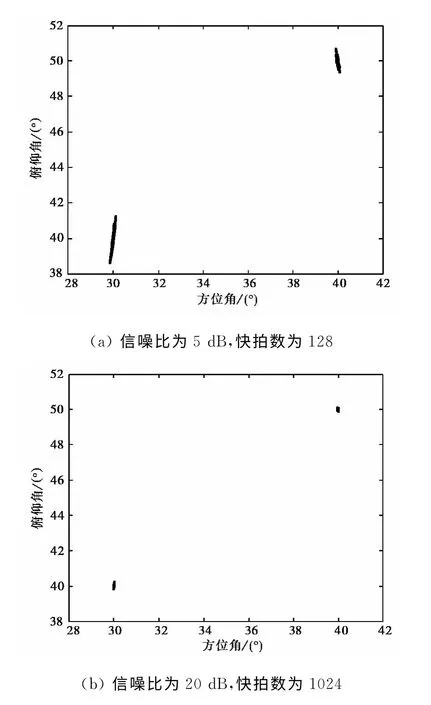
图5 方位角和俯仰角估计散布图

仿真结果分析：1）在等效孔径相同的条件下，基于四元数模型的两种算法估计标准偏差都低于基于复数模型的算法，同样说明了四元数模型优于复数模型；2）当等效孔径一样时，本文算法的估计精度高于传统Q-ESPRIT算法，这是由于本文算法解决了传统Q-ESPRIT存在的“四元数模型相干”问题，本文算法比传统算法更加充分地利用了四元数模型的正交性.

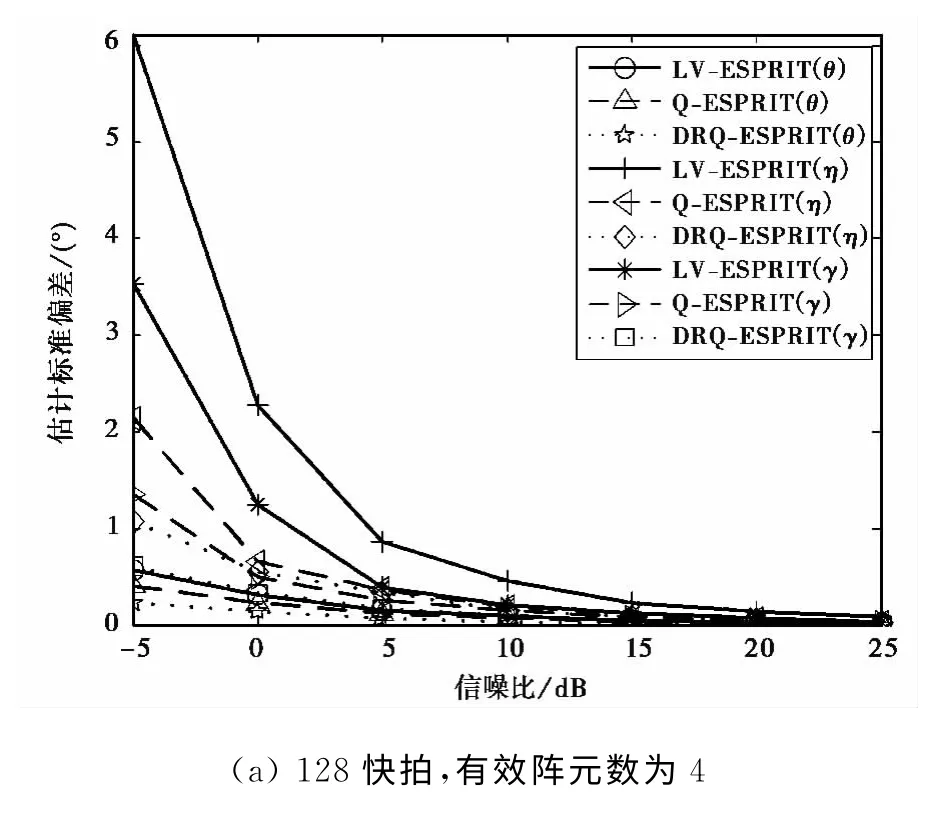
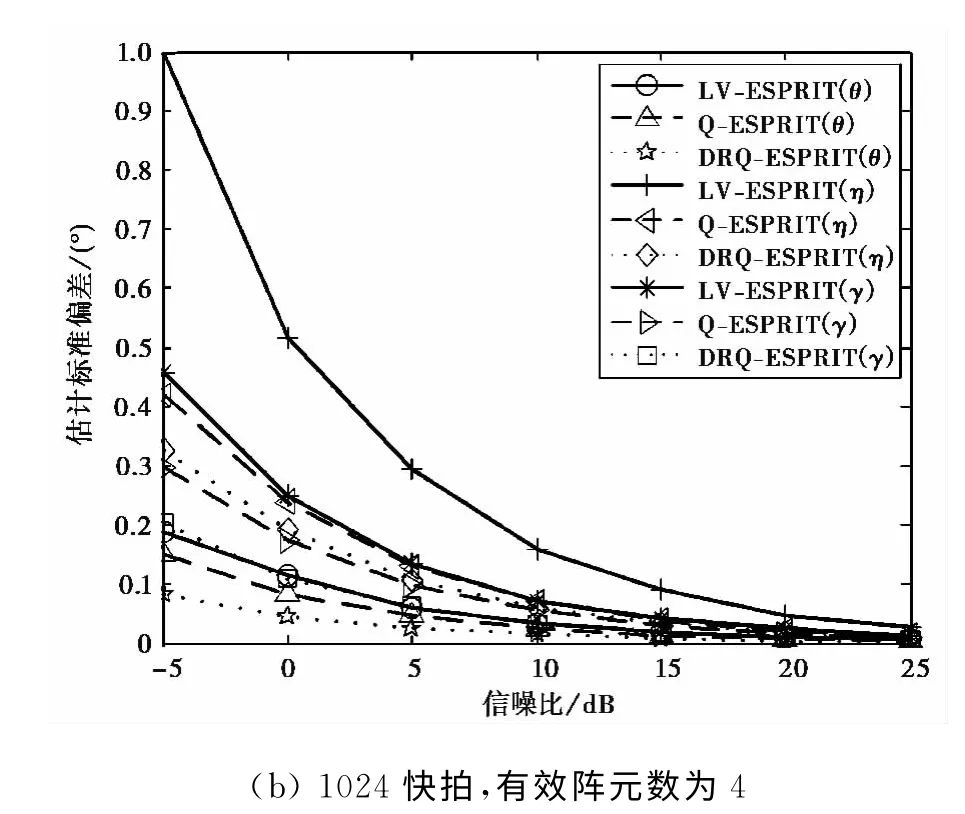
图6 估计标准偏差随信噪比的变化曲线

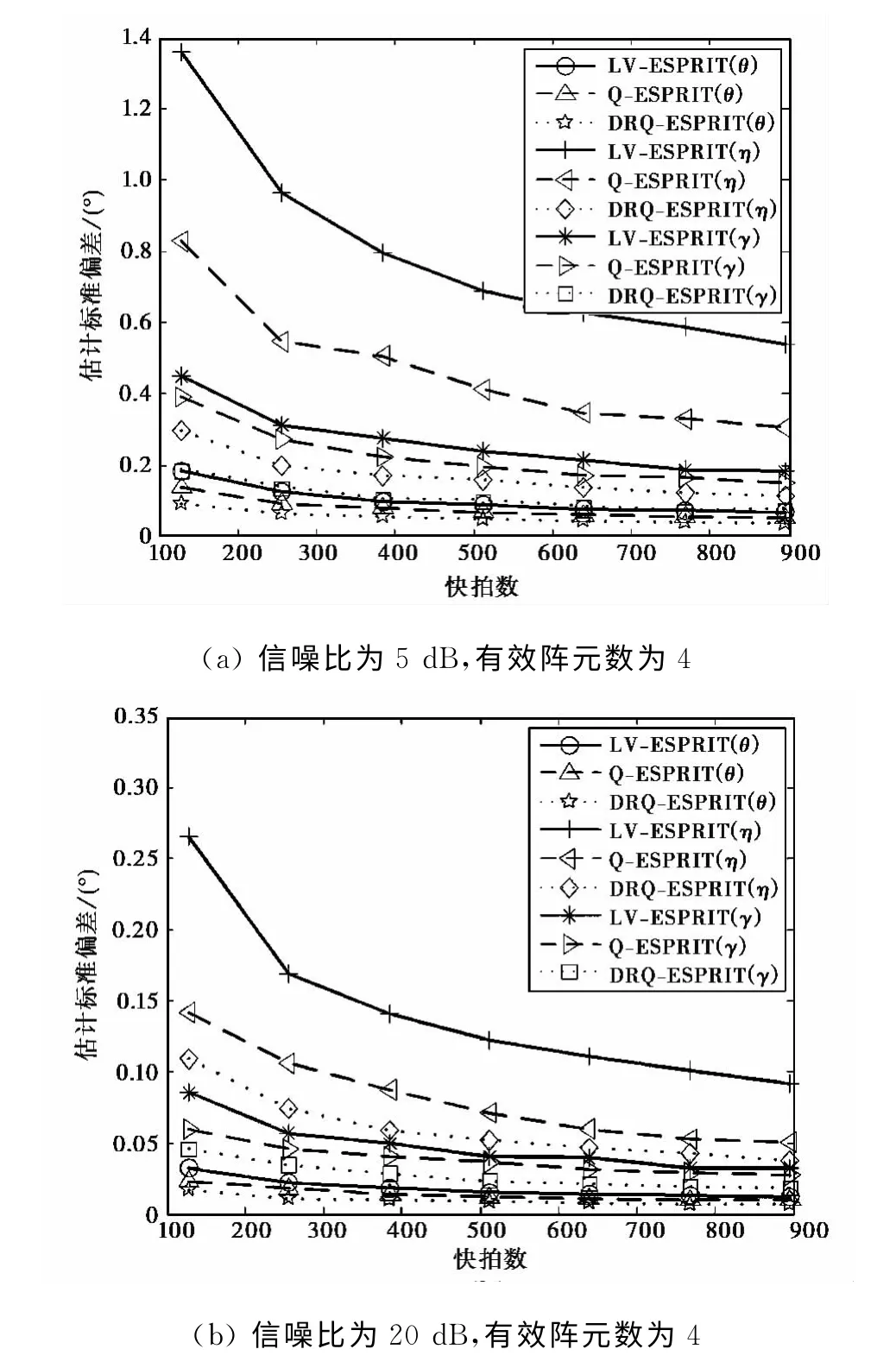
图7 估计标准偏差随快拍数的变化曲线

6 结 论

在四元数模型下，基于COLD天线组成的ULA利用传统Q-ESPRIT估计信号角度时，不仅需要入射信号方位角或者俯仰角的先验信息，并且存在“四元数模型”相干问题，导致极化信息需要通过长矢量模型进行估计.本文提出了基于互相关矩阵的降维Q-ESPRIT算法克服了该问题，无需任何入射信号方位角或者俯仰角的先验信息，充分利用四元数模型的正交性，仅通过一次四元数特征分解就可以准确地估计DOA和极化信息，运算量更低.

［1］LE BIHAN N，MARS J.Singular value decomposition of matrices of quaternions：a new tool for vectorsensor signal processing［J］.Signal Process，2004，84（7）：1177-1199.

［2］MIRON S，LE BIHAN N，MARS J I.Quaternion-MUSIC for vector-sensor array processing［J］.Transactions on Signal Processing，2006，54（4）：1218-1229.

［3］LE BIHAN N，MIRON S，MARS J I.MUSIC algorithm for vector-sensors array using biquaternions［J］.Transactions on signal processing，2007，55（9）：4523-4533.

［4］龚晓峰，徐友根，刘志文.四四元数域低秩逼近及其在矢量阵列波达方向估计中的应用［J］.北京理工大学学报，2008，28（11）：1013-1017.GONG Xiaofeng，XU Yougen，LIU Zhiwen.Quadquaternion low rank approximation with applications to vector-sensor array direction of arrival estimation［J］.Transactions of Beijing Institute of Technology，2008，28（11）：1013-1017.（in Chinese）

［5］黄家才，陶建武，温秀兰.原位误差情况下DOA和极化参数盲估计［J］.电波科学学报，2009，30（1）：179-184.HUANG Jiacai，TAO Jianwu，WEN Xiulan.Blind DOA and polarization estimation against orientation errors of vestor sensor［J］.Chinese Journal of Radio Science，2009，30（1）：179-184.（in Chinese）

［6］崔 伟，陶建武，徐惠斌.基于四元数模型的极化信号DOA估计算法［J］.电波科学学报，2007，22（增刊）：502-505.CUI Wei，TAO Jianwu，XU Huibin.The DOA estimation algorithm for polarized signals based on quaternion model［J］.Chinese Journal of Radio Science，2007，22（Sup.）：502-505.（in Chinese）

［7］李京书，陶建武.信号DOA和极化信息联合估计的降维四元数MUSIC方法［J］.电子与信息学报，2011，33（1）：106-111.LI Jingshu，TAO Jianwu.The dimension reduction quaternion MUSIC algorithm for jointly estimating DOA and polarization［J］.Journal of Electronics ＆Information Technology，2011，33（1）：106-111.（in Chinese）

［8］LI J，COMPTON R T.Angle and polarization estimation using ESPRIT with a polarization sensitive array［J］.IEEE Transaction on Antennas and Propagation，1991，39（9）：1376-1383.

［9］GONG Xiaofeng，XU Yougen，LIU Zhiwen.Quaternion ESPRIT for direction finding with a polarization sentive array［C］／／ICSP 2008Proceedings，2008：378-381.

［10］PALDI N E.Vector-sensor array processing for electromagnetic source localization［J］.IEEE Trans Signal Process，1994，42（2）：376-398.

［11］NIE Xi，LI Liping.A computationally efficient subspace algorithm for 2-D DOA estimation with Lshaped array［J］.IEEE Signal Processing Letters，2014，21（8）：971-974.