基于MCMC的分位回归GARCH模型的贝叶斯分析

曾惠芳，熊培银

(1.湖南科技大学 商学院，湖南 湘潭 411201；2. 湖南科技大学 信息与电气工程学院，湖南 湘潭 411201)



基于MCMC的分位回归GARCH模型的贝叶斯分析

曾惠芳1，熊培银2

(1.湖南科技大学 商学院，湖南 湘潭 411201；2. 湖南科技大学 信息与电气工程学院，湖南 湘潭 411201)

摘要：基于最小一乘方法提出了一类分位回归GARCH模型的2步估计方法，并且基于双指数分布和非对称Laplace分布构建了GARCH模型的似然函数，选择扩散先验分布，实现了对模型的贝叶斯估计.仿真分析发现基于最小一乘方法的贝叶斯分位回归方法可以全面有效地实现对GARCH模型的估计.

关键词：贝叶斯； 分位数； GARCH模型； 经济波动

在金融数据分析中，常常可以发现金融时间序列数据具有波动聚集性，即在较大的波动之后伴随着较大幅度的波动，较小幅度的波动之后伴随着较小幅度的波动.Engle[1]开创性地提出了自回归条件异方差(ARCH)模型，该模型假设扰动项是异方差的，并将误差滞后项的平方作为其条件方差的解释变量，从而很好地描述了时间序列的这种波动集群性.

以往研究ARCH模型的目的是测度变量的方差，而分位ARCH模型是对变量条件尺度的测度.Taylor[2]，Schwert[3]，Nelson[4]等分别都提到过利用ARCH模型研究变量分布尺度的问题.除正态分布之外，尺度比方差能够更好地描述变量的离散程度.Koenker[5]等讨论了异方差模型的分位估计，在此基础上，Koenker[6]等提出了分位自回归条件异方差模型，并推导了其估计量的渐进分布. Park[7]利用分位门限GARCH模型分析了德国马克汇率的波动性，发现分位门限GARCH模型很好地描述不同收益冲击对波动的非对称性影响.为了估计分位门限GARCH模型，把分位门限GARCH模型表示为状态空间模型，用递归分位回归方法估计了门限GARCH模型. Xiao[8]等提出了一类线性分位回归GARCH模型，并给出了模型的2步估计方法以及估计量的渐近性质.Chen[9]等提出了ARCH模型的一步估计，并提出了分位回归模型的格兰杰因果检验.本文在文献[8]研究工作基础上提出一类非线性分位回归GARCH模型，并给出了模型的贝叶斯推断.

1模型结构分析

在ARCH模型基础上，Bollerslev[10]提出了广义自回归条件异方差(GARCH)模型.GARCH模型是对ARCH模型的重要推广，比ARCH模型需要更小的滞后阶数，因此GARCH模型的结构相对简单，便于实际应用.考虑GARCH模型

(1)

传统上假设残差项服从正态分布，用极大似然方法(MLE)来估计参数，但是该方法对异常点非常敏感.随后，许多学者提出了拟极大似然方法(QMLE)，因为QMLE具有更广泛的适应范围.但是，若yt的四阶矩不存在，由QMLE得到的估计量的渐近分布将不会是正态的.针对QMLE的缺陷，Peng[11]等从估计方法的角度来处理厚尾问题，指出可以对GARCH模型做出稍许修改，即将残差平方的均值为1改为令残差平方的中位数为1.此改动相当于把原始的GARCH模型残差项乘以一个非负的常量k，可以把模型(1)表示为

(2)

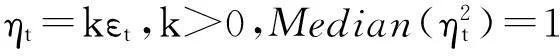
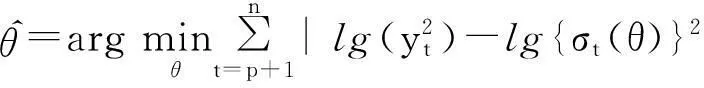
(3)

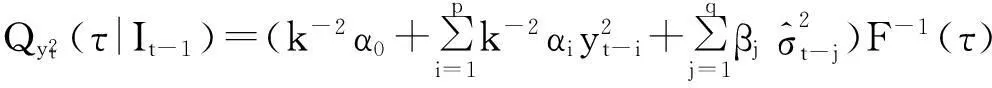
(4)

对模型进行分位回归估计；重复以上步骤，直到参数估计结果比较稳定.

2模型的贝叶斯估计

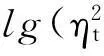
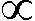
(5)

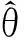
(6)

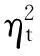
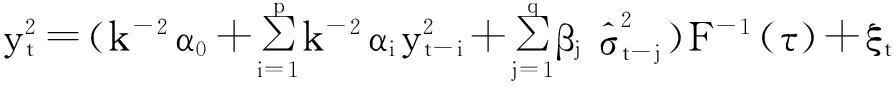
(7)

其中ξt是服从非对称Laplace分布的随机变量，ξt的τ分位数等于0.这样，分位回归GARCH模型的似然函数可以表示为

(8)

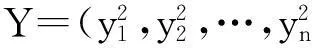
(9)

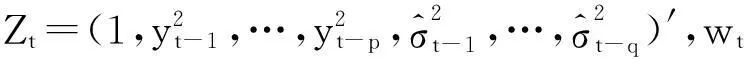
(10)

3仿真分析

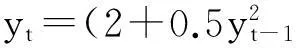
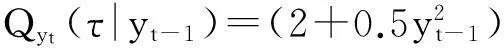
首先，通过LADE估计得到的条件方差方程中参数的全局估计.选择先验分布为均匀分布，利用MCMC算法可以模拟得到各个参数的边缘后验分布.在模型运行的过程中，一共迭代了10 500次，为确保参数估计的一致性，把开始迭代的500次丢弃，然后用501次到10 500次迭代得到的样本来估计参数.图1给出了条件方差方程中参数的迭代轨迹.从参数的迭代轨迹图可以发现各条马尔可夫链是收敛的，说明MCMC仿真过程是平稳的.图2给出了参数后验分布的核密度估计，密度曲线表现比较平滑且呈钟型，说明MCMC算法有效地模拟了模型中各参数的边缘后验分布.

图1　模型参数的迭代轨迹

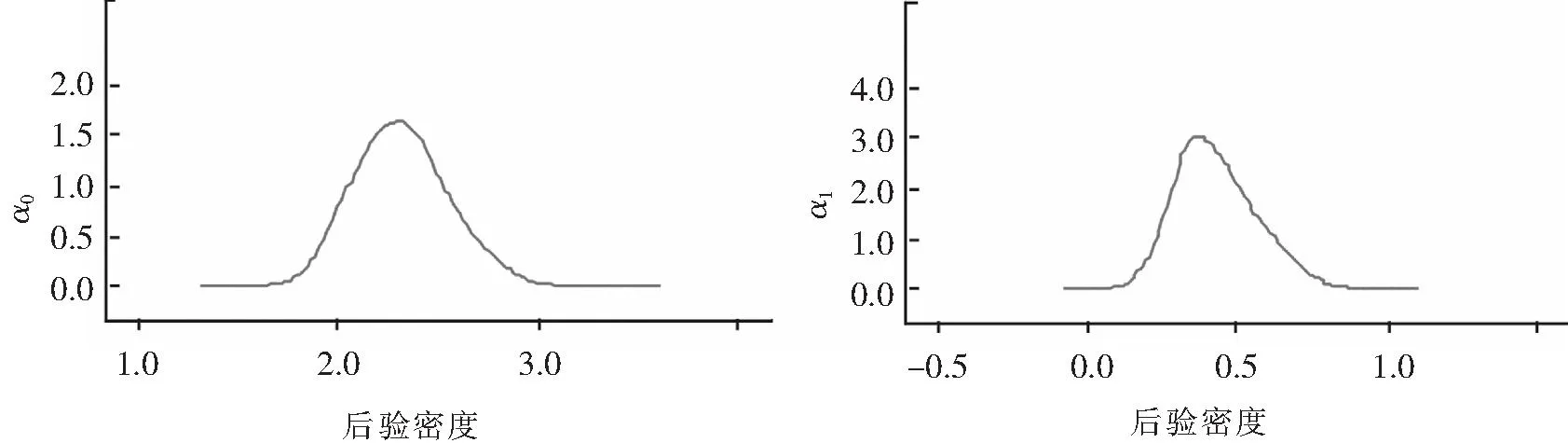
图2　模型参数的后验密度

表1给出了各参数后验均值、标准差，MC误差和95%的贝叶斯置信区间.从表1中估计结果可以看出，α0=2.325，α1=0.434 2，条件方差中的系数与数据产生过程非常接近，由此可以说明，LADE可以稳健地估计条件方差中的参数.

表1　模型的最小一乘估计

把估计得到的参数代入条件方差中，利用分位回归方法估计残差项分布的分位数.图3给出了不同分位数τ=0.1,0.25,0.5,0.75,0.9下残差项估计的后验分布.表2给出了残差项的贝叶斯分位估计.

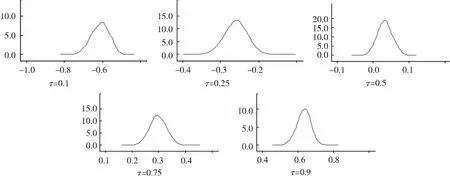
图3　残差项分位估计的后验密度

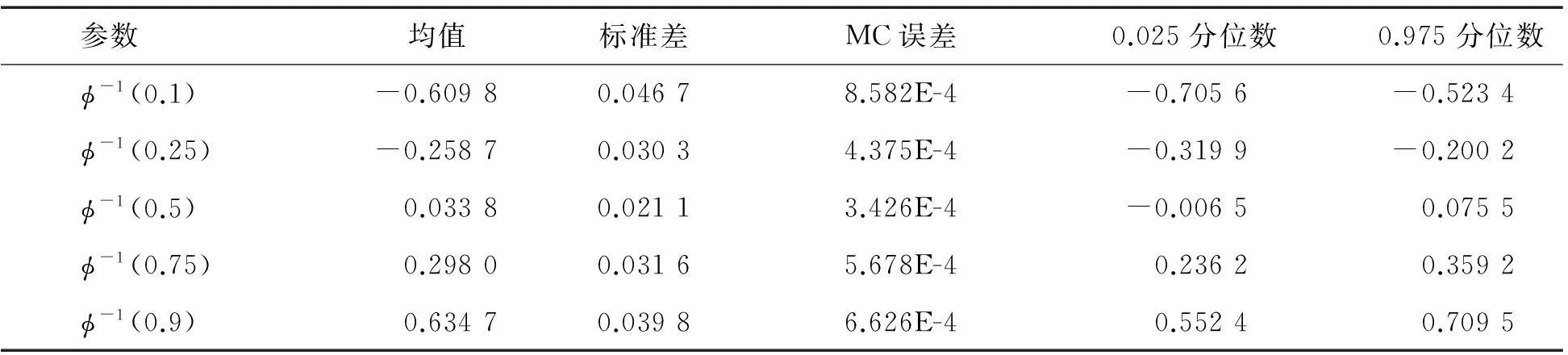
参数均值 标准差MC误差0.025分位数0.975分位数 ϕ-1(0.1)-0.60980.04678.582E-4-0.7056 -0.5234 ϕ-1(0.25)-0.25870.03034.375E-4-0.3199 -0.2002 ϕ-1(0.5)0.03380.02113.426E-4-0.0065 0.0755 ϕ-1(0.75)0.29800.03165.678E-40.2362 0.3592 ϕ-1(0.9)0.63470.03986.626E-40.5524 0.7095

从表2中可以看出，在分位数时τ=0.1,0.25,0.5,0.75,0.9时，相应的残差项的分位估计为-0.609 8，-0.258 7，0.033 8，0.298 0，0.634 7.残差项中位数估计为0.033 8，接近于零，并且残差项的估计表现出对称性.因此，从结果看说明提出的新方法是有效的，而且比文献[8]提出的方法更简单，更容易使用和理解.

4结论

GARCH模型被广泛地应用于经济金融时间序列的波动分析.由于经济金融时间序列波动的复杂性，为了更灵活全面地刻画经济时间序列的波动性，在不考虑残差项的分布形式的情况下，本文提出了一类非线性分位回归GARCH模型，并考虑到了条件方差方程中的参数的全局依赖性，基于最小一乘法提出了一种新的2步估计方法实现了对非线性GARCH模型的贝叶斯分位回归估计，得到了GARCH模型扰动项的分位估计.仿真分析发现，本文所提方法不仅可以有效地实现对分位回归GARCH 模型的估计，还可应用于其他扩展GARCH模型的估计，能够有效地识别分位回归GARCH模型中的变点问题.

参考文献：

[1] Engle R E. Autoregressive conditional heteroskedasticity with estimates of the variance of UK inflation[J]. Econometrica,1982 50:987-100 8.

[2] Taylor S. Modeling Financial Time Series[M]. [S.l.]：John Wiley & Sons, 1986.

[3] Schwert G W. Why does stock market volatility change over time?[J]. Journal of Finance, 1989, 44:1 115-1 154.

[4] Nelson D, Foster D. Asymptotic filtering theory for univariate ARCH models[J]. Econometrics,1994,62:1-42.

[5] Koenker R. Zhao Q.L-estimation for linear heteroscedastic models[J]. Journal of Nonparametric Statistics, 1994,3:223-235.

[6] Koenker R, Zhao Q. Conditional quantile estimation and inference for ARCH models[J]. Econometric Theory, 1996,12:793-813.

[7] Park B，J. Asymmetric volatility of exchange rate returns under the EMS: some evidence from quantile regression appoach for TGARCH models[J]. International Economic Journal, 2002, 16(1): 105-125.

[8] Xiao Z, Koenker R. Conditional quantile estimation for generalized autoregressive conditional heteroscedasticity models[J]. Journal of the American Statistical Association, 2009,104(488):1 696-1 712.

[9] Chen C W S, Gerlach R, Wei D C M. Bayesian causal effects in quantiles: accounting for heteroscedasticity[J]. Computational Statistics & Data Analysis, 2009,53:1 993-2 007.

[10] Bollerslev T.Generalized autoregressive conditional heteroskedasticity[J].Journal of Econometrics,1986,31:307-327.

[11] Peng L,Yao Q.Least Absolute Deviations Estimation for ARCH and GARCH models [J].Biometrika,2003,90(4):967-975.

[12] Zhou Q, Portnoy S. Statistical inference on heteroscedastic models based on regression quantiles[J]. Journal of Nonparametric Statistics, 1998, 9: 239-260.

[13] Nelson D. Conditional heteroskedasticity in asset returns: a new approach[J]. Econometrica, 1991, 59: 347-370.

Bayesian Analysis of Quantile GARCH Models Based on MCMC Algorithm

Zeng Huifang1, Xiong Peiyin2

(1. College of Business, Hunan University of Science and Technology, Xiangtan 411201，China;

2. School of Information and Electrical Engineering, Hunan University of Science and Technology, Xiangtan 411201，China)

Abstract：In the report, based on least absolute deviation, the two step estimation method for GARCH models using quantile regression was proposed, and based on double exponential distribution and asymmetric Laplace distribution, the likelihood function of GARCH model was constructed, dispersion and prior distribution was selected, and Bayes estimation for model was achieved. The simulation results showed that Bayes quantile regression estimation is effective to achieve the estimation for GARCH model.

Keywords：Bayesian; Quantile; GARCH models; economic volatility

中图分类号：F 224.9； O 212

文献标志码：ADOl：10.15886/j.cnki.hdxbzkb.2015.0022

文章编号：1004-1729(2015)02-0120-05

收稿日期：------------------------ 2014-10-25基金项目： 国家自然科学基金青年项目(41301421)

作者简介：曾惠芳(1981-)，女，湖南邵阳人，讲师，博士.