近似保正交线性映射的扰动

孔　亮

(商洛学院 应用数学研究所，陕西 商洛 726000)



近似保正交线性映射的扰动

孔亮

(商洛学院 应用数学研究所，陕西 商洛 726000)

摘要：在复Hilbert空间中,给出了近似等距的定义,给出了近似保正交线性映射的一个充分条件,得到了近似保正交线性映射的扰动定理,即证明了在一定条件下,近似保正交线性映射与近似等距的和或积是近似保正交线性映射.

关键词：扰动； 近似正交； 近似等距； 近似保正交映射

Hilbert空间中的正交性是泛函分析的重要概念之一, 由正交性定义的正交基、投影算子等概念, 丰富了Hilbert空间理论,是研究Hilbert空间的重要工具. 随着一般赋范空间几何性质的深入研究,R-正交，B-正交和I-正交等各种正交性概念被相继引入和研究, 关于正交性的研究也引起了国内学者的关注，比如文献[1]将实Banach空间中的B-正交推广为非常B-正交；文献[2]给出了Banach空间中B-正交的刻画. 近年来, 保持各种正交和近似保持各种正交映射的性质及稳定性,得到了众多学者的深入研究. 文献[3]在具体的Banach空间中给出了等距的稳定性； 文献[4]在内积空间给出了保正交线性映射的刻画； 文献[5]在有限维内积空间中给出了保正交线性映射的稳定性；文献[6]在赋范线性空间中证明了保正交线性映射是等距的常数倍；文献[7]在Hilbert空间中证明了非零近似保正交线性映射有界并且是下有界的, 并推广了文献[5]关于保正交线性映射稳定性的结论, 关于其他各种近似保正交映射已有许多研究[8-18]. 为了研究振动系统受到微小扰动后的情况,考察线性算子的各种扰动问题, 现在线性算子扰动理论已经是算子理论中的一个重要分支. 扰动理论的基本问题是:设T是线性空间的线性算子,A是扰动算子, 如何由T和A的性质导出T+A的与T相似的性质？受扰动理论基本问题的启发, 笔者研究了近似保正交线性映射的扰动, 证明在一定条件下, 近似保正交线性映射与近似等距的和或积是近似保正交线性映射.

1预备知识

H和K在本文中均表示复Hilbert空间，〈·,·〉是其内积,R表示实数集,C表示复数集.

则称U是δ-近似等距.

则称U是(δ1,δ2)-近似等距.

证明由

和

(1)

则T-1为(δ1,δ2)-近似等距, 其中δ1=1-C2-1，δ2=C1-1-1.

故T-1为(δ1，δ2)-近似等距.

推论1 设线性映射T：H→H是满射且满足‖T‖≥1和‖T-I‖<2-1，其中I：H→K是恒等映射, 则T-1为(δ1，δ2)-近似等距, 其中δ1=1-‖T‖-1，δ2=(1-‖T-I‖)-1-1.

对于ε-近似保正交线性映射, 文献[10]给出以下结论：

定理1[7]若T：H→K是ε-近似保正交线性映射, 则T有界且满足

(2)

故T为(δ1，δ2)-近似等距.

注由命题3可知, 在一定条件下,ε-近似保正交线性映射是(δ1，δ2)-近似等距. 本文给出在一定条件下, (δ1，δ2)-近似等距是ε-近似保正交线性映射, 在此基础上得到近似保正交线性映射的扰动.

2结论及其证明

引理1若U：H→K是(δ1，δ2)-近似等距, 则

(3)

证明由U是(δ1，δ2)-近似等距得

则有

和

从而

(4)

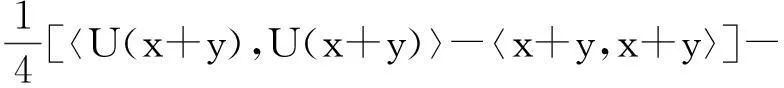
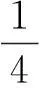
a(δ1，δ2)(‖U(x)‖2+‖U(y)‖2).

故式(3)成立.

证明 在式(3)中分别用tx,t-1y(t>0)替换x,y, 则式(3)的左边不变. 由于

min{‖U(tx)‖2+‖U(t-1y)‖2:t>0}=2‖U(x)‖‖U(y)‖，

则

(5)

在式(5)中令ε=2a(δ1，δ2), 则

(6)

证明因为T是ε-近似保正交线性映射, 所以由定理1得

农田灌溉人员在灌溉过程中忽视了节约水资源的重要性，即使采用较好的设备，很多灌溉人员也不能将设备的自身效果发挥到最大化，难以达到节约灌溉的效果，严重者还会适得其反造成严重的水资源浪费[3]。

从而

则T+U是(σ1，σ2)-近似等距. 故由定理2得,T+U是η-近似保正交线性映射, 其中η=2a(σ1，σ2).

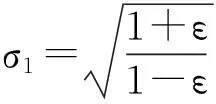
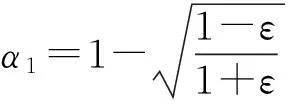
证明因为T是ε-近似保正交线性映射, 所以由定理1得

又因为U是(δ1，δ2)-近似等距, 所以

故由定理2得, TU是μ-近似保正交线性映射.

证明由定理4的证明可得.

类似定理4的证明可得

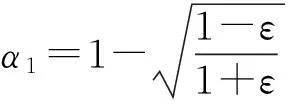
参考文献：

[1] 付向红, 黎永锦. Banach空间中非常B-正交性[J].中山大学学报(自然科学版),2008,47(1):116-117.

[2] 杨冲, 张登华. Banach空间中的Birkhoff正交性的刻画[J].数学的实践与认识,2008,38(9):187-192.

[3] Ding G G. Isometric and almost isometric operators[J]. Acta. Math. Sci.,1984,2:221-226.

[4] Chmieliński J. Linear mappings approximately preserving orthogonality[J]. J. Math. Anal. Appl.,2005, 301 (1):158-169.

[5] Chmieliński J. Stability of the orthogonality preserving property in finite-dimensional inner product spaces[J]. J. Math. Anal. Appl.,2006,318(2):433-443.

[6] Blanco A, Turnšek A. On maps that preserve orthogonality in normed spaces[J]. Proc. Roy. Soc. Edinburgh Sect. A.,2006,136(4):709-716.

[7] Turnšek A. On mappings approximately preserving orthogonality[J]. J. Math. Anal. Appl.,2007, 336(1):625-631.

[8] Chmieliński J. Remarks on orthogonality preserving mappings in normed spaces and some stability problems[J]. Banach J. Math. Anal.,2007,1(1):117-124.

[9] 孔亮,曹怀信.保正交映射与正交性方程的稳定性[J].陕西师范大学学报(自然科学版),2008,36(5):10-14.

[10] Iliševic D, Turnšek A. Approximately orthogonality preserving mappings onC*-modules[J]. J. Math. Anal. Appl.,2006,318(2):433-443.

[11] 孔亮,曹怀信.ε-近似保正交映射的稳定性与扰动[J].数学学报,2010,53(1):61-66.

[12] Chmieliński J, Wójcik P. Isosceles-orthogonality preserving property and its stability[J]. Nonlinear Anal.，2010,72(8):1 445-1 453.

[13] Mojškerc B, Turnšek A. Mapping approximately preserving orthogonality in normed spaces[J].Nonlinear Anal.,2010,73(12):3 821-3 831.

[14] Wójcik P. Linear mappings preservingρ-orthogonality[J]. J.Math.Anal.Appl.,2012,386(1):171-176.

[15] Burgos M. Orthogonality preserving linear maps onC*-algebras with non-zero socles[J]. J. Math. Anal. Appl.,2013,401(2):479-487.

[16] 张芳娟, 吉国兴.B(H)上保正交性的可加映射[J].陕西师范大学学报(自然科学版),2005,33(4):21-25.

[17] 孔亮.ε-近似保等腰正交线性映射的刻画[J].海南大学学报(自然科学版),2013,31(3):193-198.

[18] 孔亮, 李超. Hilbert空间上的(δ，ε)-近似保正交映射[J].甘肃科学学报,2014,26(4):1-4.

Perturbations of Approximate Orthogonality Preserving Mapping

Kong Liang

(Institute of Applied Mathematics, Shangluo University, Shangluo 726000，China)

Abstract：In complex Hilbert spaces, the definition of an approximate isometry was proposed, a sufficient condition for a linear mapping to be an approximate orthogonality preserving mapping was also proposed. The perturbations of an approximate orthogonality preserving linear mapping were obtained. Under certain conditions, it was proved that the sum or composition of an approximate orthonality preserving mapping and an almost isometry is an approximate orthonality preserving mapping.

Keywords：perturbation; approximate orthogonality; almost isometry; approximate orthogonality preserving mapping

中图分类号：O 177.1

文献标志码：ADOl：10.15886/j.cnki.hdxbzkb.2015.0021

文章编号：1004-1729(2015)02-0115-05

收稿日期：------------------------ 2014-10-20基金项目： 陕西省科技厅科研项目(2012JM1018);陕西省教育厅科研项目(2013JK0570);商洛学院科研项目(14SKY016)

作者简介：孔亮(1983-),男,陕西商州人,硕士,讲师.