主理想环上矩阵可对角化的新判据
邓勇
喀什师范学院数学系,新疆喀什市844006
主理想环上矩阵可对角化的新判据
邓勇
喀什师范学院数学系,新疆喀什市844006
摘要:矩阵的对角化问题在矩阵理论中占有重要地位.为将域上矩阵可对角化的结果进行推广,研究了主理想环上矩阵的可对角化问题,获得了主理想环上一类具有最小多项式m(λ)=(λ−α)(λ−β),α≠β的矩阵可对角化的充分必要条件.在此基础上,进一步证明了具有二次最小多项式的两个可对角化矩阵A,B有公共特征向量,当且仅当它们的交换子[A,B]是奇异矩阵.
关键词:主理想环;对角化;最小多项式;特征向量;交换子
1 研究现状
为方便讨论,本文用R表示有单位e¹0的主理想环;In表示n´ n阶单位矩阵;Mn(R )表示R上n´ n阶矩阵环;M1´n(R )表示R -模;GL (n , R )表示R上阶可逆n´ n 矩阵关于加法和乘法所构成的一般线性群;p (l )和m(l )分别表示矩阵A的特征多项式和最小多项式;[A , B ]=AB- BA表 示矩阵A,B的交换子.
若用相似变换可将AÎ Mn(R )化为对角矩阵,则称其可对角化.即$UÎ GL(n , R )使得.因此,若AÎ Mn(R )可对角化,则其特征多项式p(l )可写为的形式.其中aiÎ R互不相同,ki,(i=1,2,L,r )是非负整数.显然,若可对角化,则其最小多项式m(l )无重根,即.特别地,若R=F是域,则最小多项式无重根是域F上的矩阵A可对角化的充要条件[1].但是,对有单位的交换环(尤其是主理想环R )上的矩阵而言,最小多项式无重根只是其可对角化的必要条件,而非充分条件[2].除此之外,类比域上的矩阵可对角化条件,文献[3]证明了AÎ Mn(R )可对角化Ûp(l )有n个互异特征值a1,a2,L,an;文献[4]证明了AÎ Mn(R )可对角化A有对应特征值a1,a2,L,an(不必互异)的 n个不同的特征向量,且它们构成R -模M1´n(R )的一组基底.然而,因基特征向量的计算十分繁琐且无一般算法,故实际操作相当困难.
本文进一步研究Mn(R )上具有二次最小多项式m(l )=(l-a)(l-b)的矩阵可对角化的判定问题,其中a,bÎ R且a¹b.在此基础上,给出了A, BÎ Mn(R )存在公共特征向量的条件.
2 判别定理
设AÎ Mn(R )且rankA=k是幂等矩阵.众所周知,幂等矩阵的最小多项式为 m(l )=l (l-e )且$UÎ GL(n , R )使得UAU-1=diag (Ik,0 ) ,即其可对角化[5].下面,我们来描述Mn(R )中具有二次最小多项式m(l )=(l-a)(l-b),(a¹b )的可对角化矩阵的特征.
定理1设AÎ Mn(R )且其中a,bÎR ,a¹b, 1£ k£ n.矩阵A可对角化,即$TÎ GL(n , R )使得下列两个条件
(i)m (l )=(l-a)(l-b)是A的最小多项式;
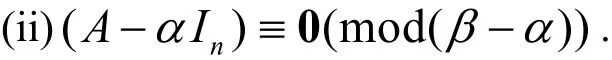
同时成立.
证明(必要性)设AÎ Mn(R )的特征多项式,其中a,bÎR,a¹b, 1£ k£ n且A可对角化,即$TÎ GL(n , R )使得.显然,m (l )=(l-a)(l-b)是A的最小多项式.又因故必要性得证.
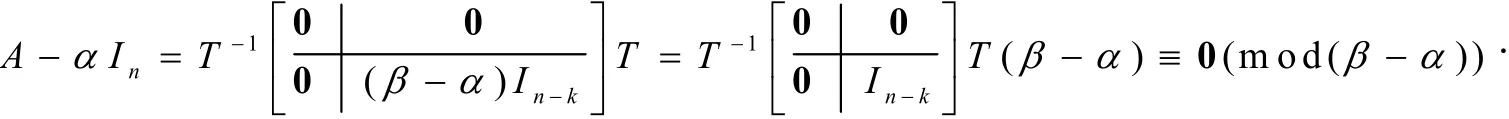
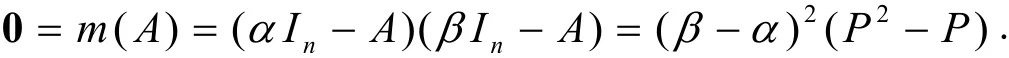
因a¹b,故由上式可得P2=P,即是幂等矩阵.又因且P可对角化,故A可经相似变换化为的形式,即A可对角化.充分性得证.
推论1设AÎ Mn(R )且m(l )=(l-a)(l-b),其中a,bÎ R 且a¹b.若(a-b )是 R中的单位的因子,则A可对角化.
推论2设AÎ Mn(R )且m(l )=(l-a)(l-b),其中a,bÎ R且a¹b.若A可对角化,则存在唯一一对幂等矩阵Pa, PbÎ Mn(R )使得
证明(存在性)设AÎ Mn(R )且m(l )=(l-a)(l-b),其中a¹b.若A可对角化,则首先由定理1的充分性证明可知,矩阵A可表为A=aIn+(b-a)Pb,其中PbÎ Mn(R )是幂等矩阵,即(a)成立.其次,令Pa=In- Pb.显然它也是幂等矩阵.于是得Pa+ Pb=In,即(b)成立.再次,由(b)可知Pb=In- Pa,因此,(a)可改写为A=aIn+(b-a)(In- Pa)=bIn+(a-b)Pa,即(c)成立.最后,由(b)可将(a)表为A=a(Pa+ Pb)+ (b-a)Pb=aPa+bPb,即(d)成立.
(唯一性)对于矩阵A,假设还存在不同于{Pa, Pb}的另一幂等矩阵对{Qa, Qb},并且它们也满足等式(a)-(d).因A=aIn+(b-a)Pb=aIn+(b-a)Qb且a¹b,故有Pb=Qb.同理可证Pa=Qa.
在此,我们强调上述结果对初等除环上的矩阵同样正确.此外,对特殊环上的矩阵,其中有些结果还可进一步拓展.例如,有单位的交换环上的幂等矩阵可对角化[6].同时,也提请读者注意:在主理想环中虽具有二次最小多项式,但不能对角化的矩阵分类与相似变换之间的关系至今仍未得到彻底解决.
3 结果运用
设A, BÎ Mn(R ).若$uÎM1´n(R )使得uA=u a(Au=a u)且uB=u b(Bu=b u) ,其中a,bÎ R,则称A , B有公共的左(右)特征向量.显然,若A , B在R上有公共的左特征向量,则它们在R上必有公共的右特征向量.因此,下文所称A , B有“公共的特征向量”意指A , B有公共的左特征向量.容易证明:若A , B在R上仅有一个公共的特征向量,则A , B的特征多项式p(l )和q(l )能够表成p(l )=(l-a)c (l )和q(l )=(l-b)d (l )的形式.特别地,当R=F是域时,矩阵A, BÎ Mn(F )存在公共特征向量的问题已基本解决[7,8].
定理2幂等矩阵A, BÎ Mn(R )有一个公共的特征向量Û交换子[A , B ]是奇异矩阵.
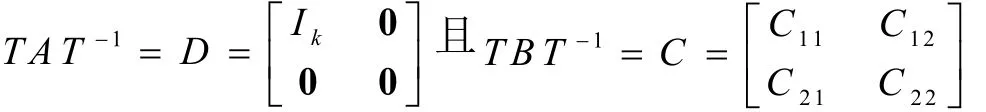

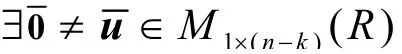
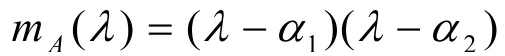
参考文献
[1] Matoušek J.MathematicalandAlgorithmicApplicationsof LinearAlgebra[M].USA:American Mathematical Society, 1991
[2]魏慧敏.可交换矩阵的对角化问题[J].哈尔滨师范大学学报(自然科学版),2013,29(5):15-17
[3]黄允宝.关于可对角化线性算子的一点注记[J].杭州师范大学学报(自然科学版),2010,9(5):4-6,17
[4] Prokip V. On similarity of matrices over commutative rings [J]. Lin. Alg. Appl., 2005(399):225-233
[5]张慧.对幂等矩阵的研究[J].陕西科技大学学报(自然科学版),2012,30(6):139-142
[6]王羡,王登银,刘笑颖.交换环上幂等矩阵的对角化和秩[J].中国矿业大学学报,2009,38(6):909-912
[7]赵可琴,张小凯,陈铁生.两矩阵的公共特征向量与同时三角化探讨[J].许昌学院学报,2012,31(5):122-125
[8] TsatsomerosM.Acriterionfortheexistenceofcommoninvariantsubspacesofmatrices[J].Lin.Alg.Appl.,2001(322):51-59
New Diagonalization Condition for Matrices in a Domain of Principal Ideal
DENG Yong
Department of Mathematics/Kashgar Teacher’s College, Kashgar 844006, China
Abstract:The diagonalization of matrices has an important position in the matrix theory. In order to expand the results for diagonalization of matrices over fields, we discussed the diagonalization of matrices over a domain of principal ideals, and obtained the necessary and sufficient conditions of diagonalization of matrices over a domain of principal ideals with minimal polynomial m(λ)=(λ−α)(λ−β),α≠β. Further, on the basis of the obtained results, the conditions under which the matrices A and B have common eigenvectors if and only if their commutator [A, B] is singular matrix, was proved.
Keywords:Domain of principal ideals; diagonalization; minimal polynomial; eigenvector; commutator
作者简介:邓勇(1967-),男,四川遂宁人,学士,教授,硕士生导师,主要从事矩阵及其数值计算研究. E-mail:dengy-ks@sohu.com
基金项目:国家社科基金项目(11XTJ001)
收稿日期:2015-01-11修回日期: 2015-03-02
中图法分类号:O151.21; O157.3
文献标识码:A
文章编号:1000-2324(2015)04-0625-03

