改进的果蝇优化算法在城市物流配送中心选址中的应用

于博

郑州轻工业学院经济与管理学院,河南郑州450002



改进的果蝇优化算法在城市物流配送中心选址中的应用

于博

郑州轻工业学院经济与管理学院,河南郑州450002

摘要:为实现物流配送中心选址的合理配置，本文提出一种基于Logistic混沌系统的果蝇优化算法，通过我国31个城市物流配送中心坐标及其需求量的要求，建立物流配送中心选址的数学模型，并运用其算法进行优化求解，实现配送路径的优化配置，节约成本。该改进的果蝇优化算法既充分发挥Logistic混沌系统和果蝇优化算法的优点，又克服了果蝇优化算法的局部最优问题。仿真结果表明该算法具有收敛速度快、精度高的优点。

关键词:果蝇优化算法;物流配送中心;选址

随着电子商务的快速增长，物流业作为一个新兴行业正在迅速发展。物流配送中心作为连接客户和供应商的中间纽带，其选址方式决定了物流配送方式和配送距离，影响物流系统的工作效率和经济效益，研究物流配送中心的选址具有重要的现实意义和理论价值。

1　改进的果蝇优化算法

1.1果蝇优化算法

果蝇优化算法(Fruit Fly Optimization Algorithm, FOA)[1]具有控制参数少、收敛速度快和收敛精度高的优点，但其存在局部最优问题，容易陷入局部极小值的缺点。本文结合Logistic混沌系统具有遍历性、规律性和随机性的优点，提出一种基于Logistic混沌系统的果蝇优化算法，克服果蝇优化算法的局部最优问题。

果蝇优化算法具体流程如下[2]：

（1）设置果蝇优化算法的果蝇群体大小Popsize和最大迭代次数Iteration，随机初始化果蝇群体位置，初始化结果分别用X_begin和Y_begin表示；

（2）根据公式（1）和公式（2）计算果蝇个体进行寻优的随机方向和距离；

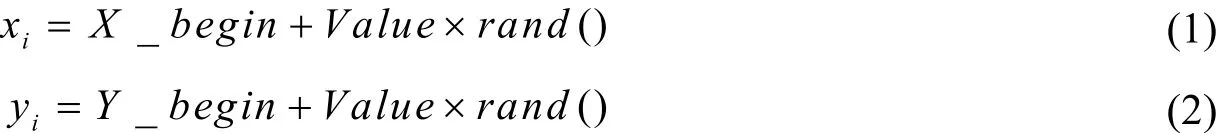
公式（1）和公式（2）中，Value表示果蝇的搜索距离；xi和yi分别表示果蝇个体的下一时刻的位置。

（3）根据公式（3）估计果蝇个体和原点之间的距离ai，之后运用公式（4）计算果蝇个体的味道浓度si；

（4）味道浓度si代入公式（5）味道浓度判定函数，计算出该果蝇个体当前位置的味道浓；

（5）找到果蝇群体中最佳味道浓度值和最佳位置，最佳味道浓度由Smellb表示，最佳位置由xb和yb表示；

（6）保留并记录果蝇最佳位置和最佳味道浓度，最佳味道浓度Smellbest=Smellb，果蝇初始位置X_begin=xb，Y_begin=yb，同时果蝇群体朝着该最佳位置搜寻过去；

（7）进入迭代寻优，重复迭代步骤（2）~（5），同时判断味道浓度是否好于前一迭代味道浓度；若成立，则执行步骤（6）。

1.2Logistic混沌系统

已知Logistic混沌系统的表达式如公式（6）所示[3]：

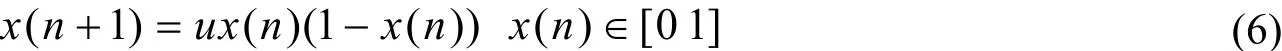
公式（6）中，n表示迭代次数；u表示混沌控制参数，当u=4时，Logistic系统处于混沌状态。混沌变量Cxi的一种变换计算公式如（7）所示：

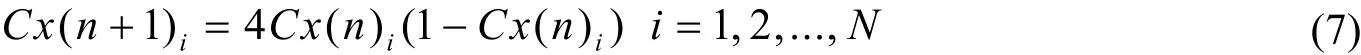
公式（7）中，Cx(n)i表示混沌映射的第i个混沌变量Cxi在第n步混沌变量之后的值，当Cxiϵ[0 1]，并且CxiÏ{0.25, 0.50, 0.75}时，系统处于混沌状态。公式（7）的优化参数xiϵ[aibi]，可通过公式（8）和公式（9）同混沌变量Cxiϵ[0 1]进行相互映射变换。

公式（9）中，x´i表示混沌映射之后的第i个混沌变量Cxi转化成常规变量的值。

1.3改进的果蝇优化算法

改进的果蝇优化算法的主要流程如下：

（1）设置果蝇优化算法的果蝇群体大小Popsize和最大迭代次数Iteration，随机初始化果蝇群体位置，处于[0 1]之间，并用行向量Zi表示；

（2）根据公式（8）将Zi分量映射成混沌变量Cz(n)i，Cz(n)i=[0 1]；

（3）运用公式（7）对混沌变量Cz(n )i进行混沌映射；

（4）利用公式（9）对每个分量进行映射变换，映射为处于[aibi]之间的常规变量，并计算适应度f()，选取种群中最小的f()，记录选取的最小f()，fit(gen )=f ()；

（5）进行寻优迭代处理，重复流程（2）~（4）；

（6）若停止条件满足，则选择最小fit，使得Smellbest=min(fit (gen ))，此时记录最小f()所对应的味道浓度Sg；

（7）为了保证要获得的初值在初次迭代的最优参数的小领域内，如果参数大于0，则Bϵ[0 1]，通过反复验证，本文选取B=0.25，在选取的味道浓度Sg附近运用Si=Sg+2B´ rand()- B 生成微小扰动种群，同时运用Si评估f(Si)，选取种群中适应度最小的f(Si)，并令Bestsmell=min(f(Si))，如果Bestsmell˂Smellbest，那么则Smellbest=Bestsmell，令Sg=Si；

（8）进行二次迭代寻优，更新味道浓度Si，重复步骤（7）；

（9）若停止条件满足，输出Smellbest，P=Sg。

2　物流配送中心选址数学模型

为了实现城市物流配送中心的最优选择，进行如下假设[4]：

（1）物流配送中心的物资容量总能够满足各需求点的物资需求，并且配送中心的物资总量由其配送需求点的物资需求量决定；

（2）一个配送中心仅供应一个需求点；

（3）不考虑物流配送中心到工厂的运输费用。

基于上述假设，可以建立物流配送中心选址的数学模型，其配送示意图如图1所示。该数学模型是一个选址和分配模型，在满足距离上限的条件下，需要从n个需求点中找出配送中心并向各需求点配送物品[5]。目标函数是各配送中心到需求点的需求量和距离的乘积之和最小，目标函数为：

约束条件：

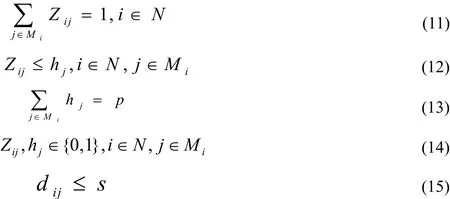
其中，N={1, 2,...,n }是所有需求点的序号集合；Mi表示到需求点i的距离小于s的备选配送中心集合，iN, MiN ；wi表示需求点的需求量；dij表示从需求点i到离它最近的配送中心j的距离；Zij表示0~1变量，表示用户和物流中心的服务需求分配关系，当Zij=1时，表示需求点j的需求量由配送中心j供应，否则Zij=0；hj表示0~1变量，当hj=1时，表示需求点j被选为配送中心；s表示新建配送中心由它服务的需求点的距离上限。

公式（11）保证每个需求点只能由一个配送中心服务；公式（12）确保需求点的需求量只能被设为配送中心的点供应，即没有配送中心的地点不会有客户；公式（13）规定了被选为配送中心的数量为p；公式（15）保证了需求点在配送中心可配送到的范围内。

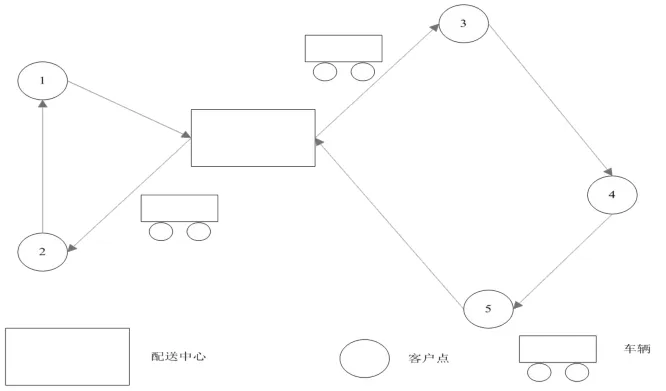
图1　配送示意图Fig.1 Schematic diagram for distribution

3　IFOA算法优化物流配送中心选址

IFOA算法优化物流配送中心选址的步骤如下，流程图如图2所示：

Step 1：设定IFOA算法的种群大小Popsize，最大迭代次数Iteration；

Step 2：根据适应度函数公式（10）计算果蝇个体的适应度函数值，寻找果蝇个体和全局最优个体的位置和最优值；

Step 3：果蝇种群速度和位置的更新；

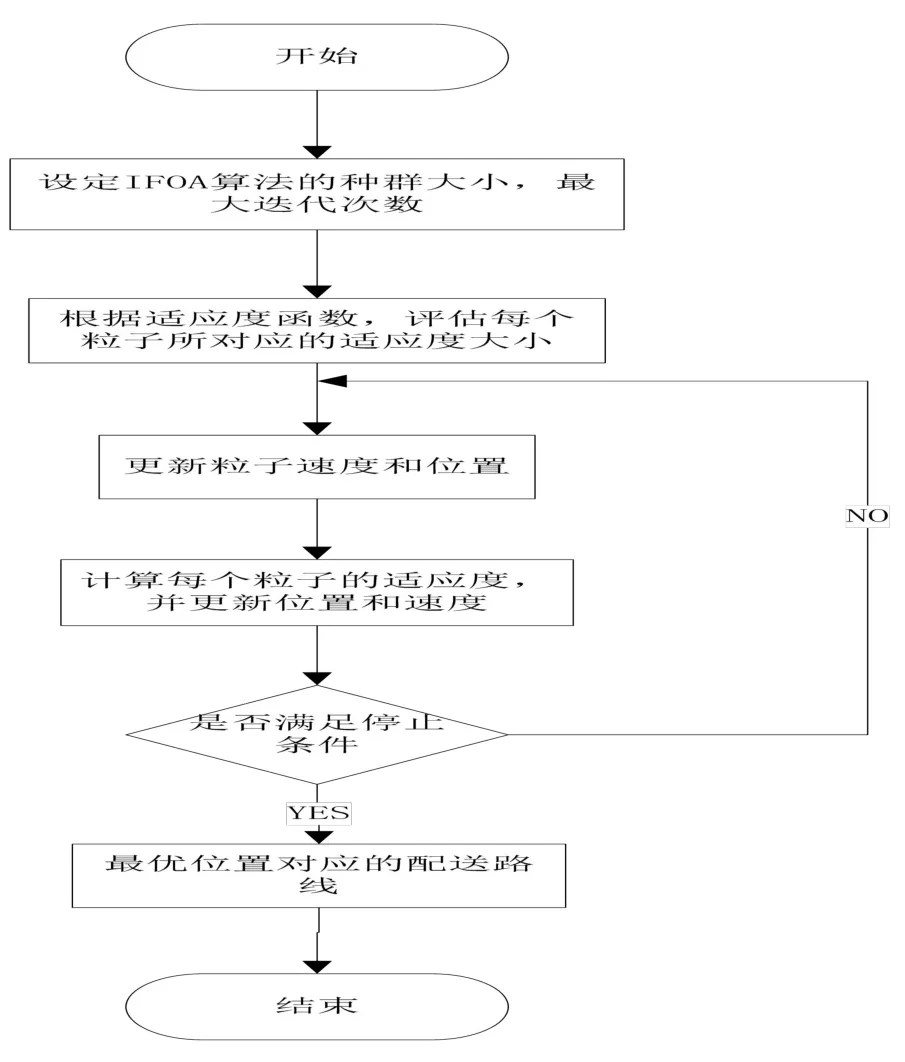
图2　IFOA算法优化物流配送中心选址的流程图Fig.2 Flow chart for optimizing logistics distribution center location based on IFOA

Step 4：计算适应度同时更新位置和速度；

Step 5：若gen˃Iteration，保存最优解；反之gen=gen+1，转到Step3;

Step 6：根据最优位置对应的物流配送中心的最佳位置和最优配送路径。

4　实验仿真

为了证明改进的果蝇优化算法进行物流配送中心选址优化选择的可行性和有效性，收集中国31个城市的坐标，每个用户的位置和其物资需求表如表1所示，本文数据是经过规范化处理之后的数据，从中选择6个作为物流配送中心[6]。设定果蝇种群规模Sizepop=20，最大迭代次数Iteration=100，物流配送中心的优化结果如图4~7所示：

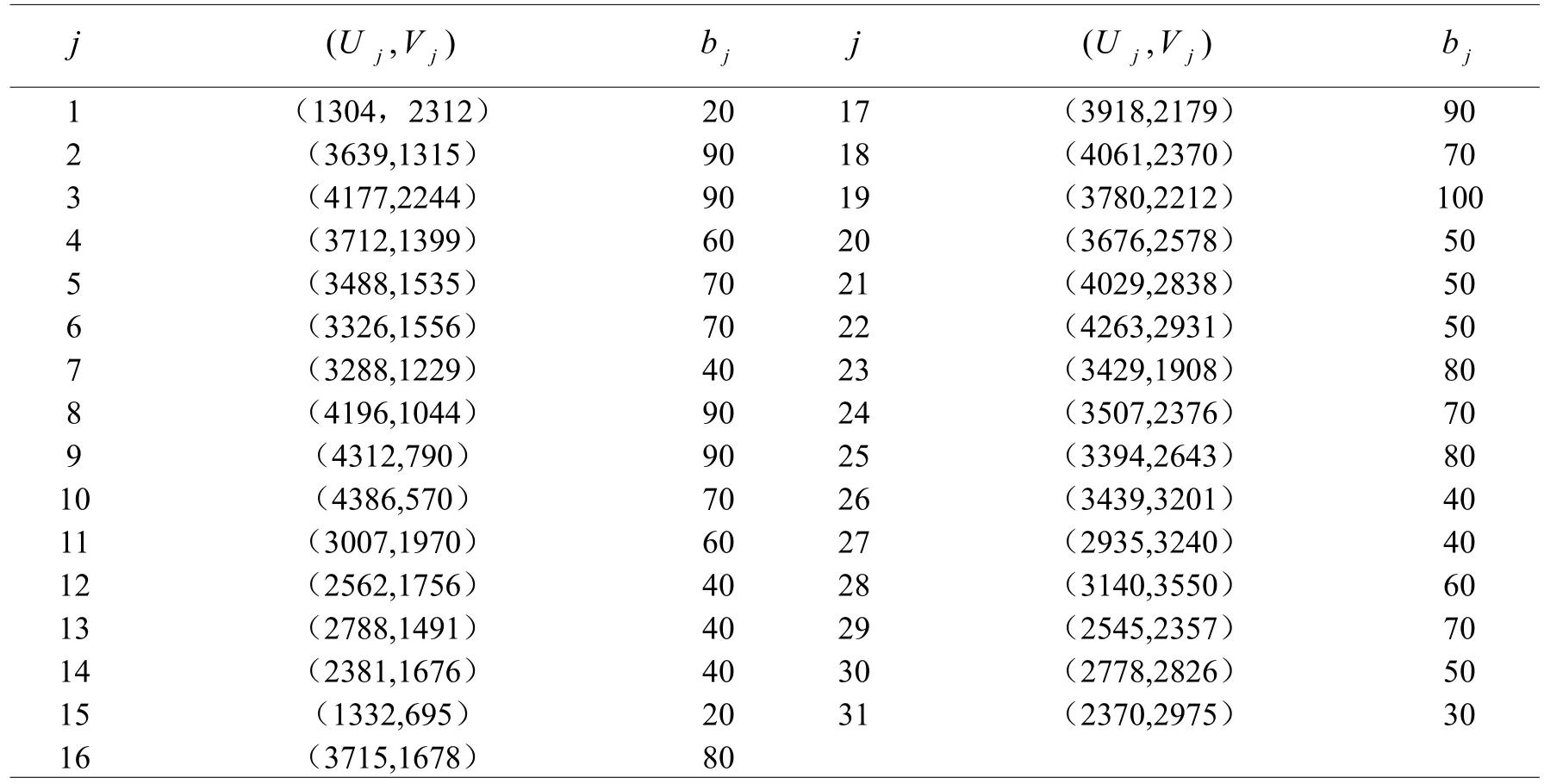
表1　用户位置和其物资需求量Table1 Users´location and their material demand

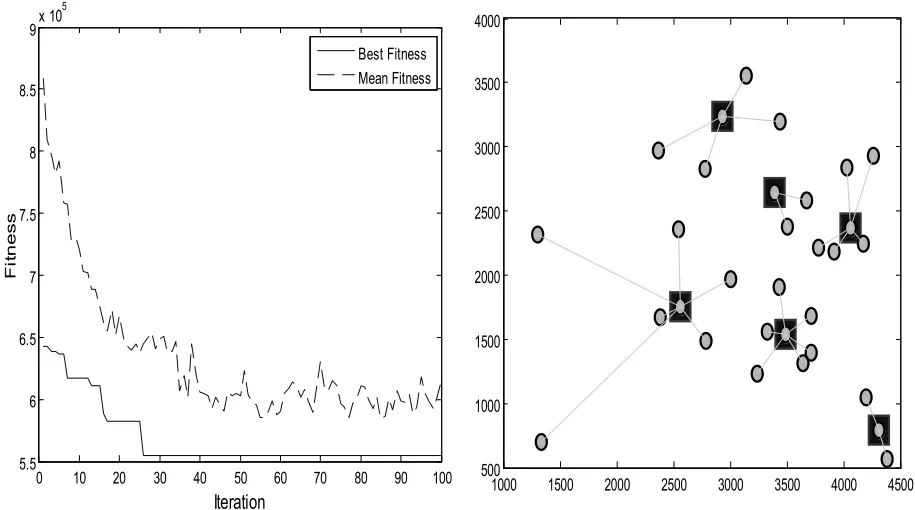
图4　配送中心为4时，配送路线和收敛图Fig.4 The delivery route and convergence when distribution center is 4

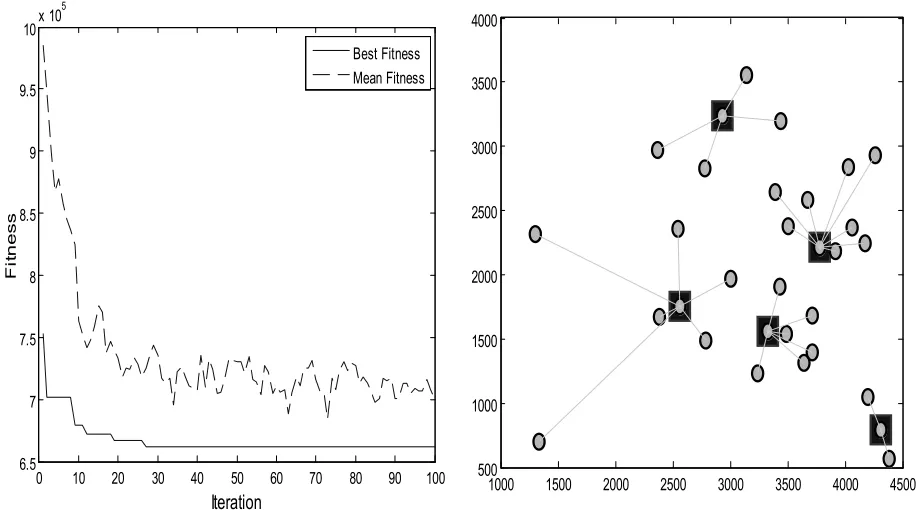
图5　配送中心为5时，配送路线和收敛图Fig.5 The delivery route and convergence when distribution center is 5

图6　配送中心为6时，配送路线和收敛图Fig.6The delivery route and convergence when distribution center is 6

图7　IFOA、FOA收敛性对比图Fig.7 Comparison of convergences between IFOAand FOA

通过IFOA算法在不同迭代次数和不同种群大小条件下，物流配送中心选址收敛曲线和最优配送路径的优化结果可知，随着迭代次数和种群规模的增加，其最佳配送路径趋于更优，通过仿真实验可知，IFOA算法优化物流配送中心选址问题具有很高的可行性和有效性，效果较好。

5　结论

为了实现物流配送中心选址位置的合理配置，提高物流配送系统的工作效率和经济效益，本文针对果蝇优化算法具有控制参数少、收敛速度快和收敛精度高的优点，但其存在局部最优问题，容易陷入局部极小值的缺点，结合Logistic混沌系统具有遍历性、规律性和随机性的优点，提出一种基于Logistic混沌系统的果蝇优化算法，克服果蝇优化算法的局部最优问题。通过我国31个城市物流配送中心坐标和其物资需求量的要求，建立物流配送中心选址的数学模型，并运用改进的果蝇优化算法进行优化求解，实现配送路径的最优化配置，节约成本。仿真结果表明该算法具有收敛速度快、精度高的优点。

参考文献

[1] Wen-Tsao Pan. A new fruit fly optimization algorithm: Taking the financial distressmodel as an example[J]. Knowledge-Based Systems,2012(26):69-74

[2] Arumugam MS, Rao MVC, TanAWC.Anovel and effective particle swarm optimization like algorithm with extrapolation technique[J].Applied Soft Computing, 2009,9(1):308-320

[3]姜大立,杜文.易腐物品物流配送中心选址的遗传算法[J].西南交通大学学报,2003(2):62-67

[4]赵冬玲,于龙振,陈常菊.基于混合遗传算法的多配送中心选址问题研究[J].物流技术,2008(6):40-42

[5]吴兵,罗荣桂,彭伟华.基于遗传算法的物流配送中心选址研究[J].武汉理工大学学报:信息与管理工程版,2006,25(2):89-91

[6] Lin Cheng-Jian, Liu Yong-Cheng. Image backlight compensation using neuron-fuzzy networks with immune particle swarm optimization[J]. Expert Systems with Applications, 2009(3):12-20

·科研资讯速递·

Application of the Improved Fruit Flying Optimization Algorithm in Urban Logistics Distribution Center Location

YU Bo

School of Economics and Management/Zhengzhou University of Light Industry, Zhengzhou 450002, China

Abstract:To realize the reasonable allocation in logistics distribution center location, this paper provided a fruit flying optimization algorithm based on Logistic chaotic system to optimize the logistics distribution center location through the mathematics model set up on 31 urban logistics distribution center coordinates and the material demand quantity requirements in China and to achieve the optimization allocation in delivery routes and save a cost. This improved algorithm fully takes advantages of Logistic chaotic system and fruit flying distribution algorithm and overcomes the defects of them so as to show the advantages of fast convergence and high accuracy in simulation examples.

Keywords:Fruit flying optimization algorithm; logistics distribution center; location

作者简介:于博(1980-),男,河南汝州人,硕士,讲师,研究方向:电子商务、物流. E-mail:boyu13@gmail.com

基金项目:河南省科技公关项目“农产品冷链物流体系建设及关键冷链技术研究”(112102310055)

收稿日期:2014-06-13修回日期: 2014-07-22

中图法分类号:F22

文献标识码:A

文章编号:1000-2324(2015)04-0632-04