硬质合金内冷钻头三维参数化建模研究

潘俊浩,卓勇,连云崧,张祥雷

(厦门大学物理与机电工程学院, 361005, 福建厦门)



硬质合金内冷钻头三维参数化建模研究

潘俊浩,卓勇,连云崧,张祥雷

(厦门大学物理与机电工程学院, 361005, 福建厦门)

针对硬质合金内冷钻头结构复杂、尺寸多、建模难度大的问题,进行三维参数化建模,在UG软件中建立了三维参数化设计系统。按照设计参数,首先将端刃截形沿螺旋线扫掠,生成内冷钻头的螺旋槽模型。其次,与传统麻花钻的钻尖仅包含单曲面或双曲面不同,内冷钻头的钻尖包含了第一后刀面、第二后刀面等多个曲面;根据端刃第一后角、第二后角、Gash角等具体参数,建立了第一后刀面、第二后刀面、Gash面等钻尖曲面的模型。在细节处理部分,由于退刀槽由光滑曲面过渡衔接而成,难以通过数学模型的方式进行建模,因此利用UG强大的曲面造型功能,使用桥接曲线、网格曲面等操作,生成了过渡自然的退刀槽模型。运行实例表明,硬质合金内冷钻头三维参数化设计系统能够根据设计需要快速完成三维模型的建立,生成的模型准确描述了螺旋角、端刃后角、Gash角等关键参数,在退刀槽等细节部位过渡自然,实现了硬质合金内冷钻头三维模型的精确表达。

硬质合金内冷钻头;数学模型;参数化建模;二次开发

内冷钻头的研究在日本、德国、瑞典等西方发达工业国家取得了成功,但我国对于内冷钻头的研究仍处于起步阶段[1]。内冷钻头包含了大量的复杂曲线和复杂曲面,传统的手工绘图设计过程中需要很多的计算,工作量大,且模型修改困难,不利于产品的系列化设计。使用CAD软件进行交互式设计,只是将画图环境从纸上转移到了计算机上,并不能提高设计的效率。因此,建立准确的数学模型对内冷钻头的各个结构进行描述并应用于三维参数化建模具有重要的现实意义。

准确的数学模型和三维模型的精度是制约硬质合金内冷钻头设计效率的主要因素。目前,国内外学者针对内冷钻头或麻花钻头的数学模型及三维参数化建模做了大量的研究。文献[2]提出了一个通用的数学模型,用以描述包括锥形钻头、双曲面钻头、椭球钻头等不同类型钻头的钻尖,但这个模型因为针对的是普通的麻花钻头,不适用于目前的内冷钻头。文献[3]建立了直线刃的圆锥面刃磨法数学模型,并给出了刃磨标准麻花钻所需的工艺参数。刃磨方法是国内学者在进行麻花钻头钻尖三维建模时使用最广泛的方法。文献[4-6]对麻花钻的钻尖几何形状进行优化,减小了麻花钻钻尖在钻削时的推力和转矩。文献[7-11]介绍了在大型三维软件(如UG、Pro/E)中建立内冷钻头或麻花钻头的三维模型,通过二次开发的形式控制模型的变化,但建立的模型在退刀槽等细节部位的过渡不够自然,不能做到三维模型的精确表达。

虽然针对内冷钻头或麻花钻头的数学模型已做了大量的研究,但是涉及钻尖部位的建模多是采用文献[3]介绍的圆锥面刃磨法。这种方法适合标准的麻花钻头,由于内冷钻头钻尖部分结构和普通麻花钻不同,该方法并不适用于内冷钻头的设计。目前在钻头的细节处理方面,退刀槽部位的建模研究较少,过渡大都不够自然。

硬质合金是内冷钻头普遍采用的材料,对硬质合金内冷钻头进行研究具有一定的代表性。因此,本文以硬质合金内冷钻头为研究对象,针对上述问题,分析其几何结构,研究适用于硬质合金内冷钻头的钻尖模型,建立了精确的硬质合金内冷钻头数学模型;运用UG软件,基于二次开发技术,在程序中实现了硬质合金内冷钻头三维参数化精确建模,生成的模型符合设计参数,保证了结构准确性,可有效应用于后续的加工仿真及工艺设计。

1 硬质合金内冷钻头基本结构

全面了解硬质合金内冷钻头的基本结构是进行精确建模的基础。硬质合金内冷钻头结构与传统麻花钻头相比,由于存在冷却孔,大大提高了冷却效率。为适应高硬材料的钻削,硬质合金内冷钻头的钻尖部分结构需要在传统麻花钻的基础上进行改进。

硬质合金内冷钻头主要由钻尖、导屑槽、螺旋槽、退刀槽、刀柄、冷却孔等6部分组成,具体结构见图1。下面对钻尖和退刀槽部分进行介绍。

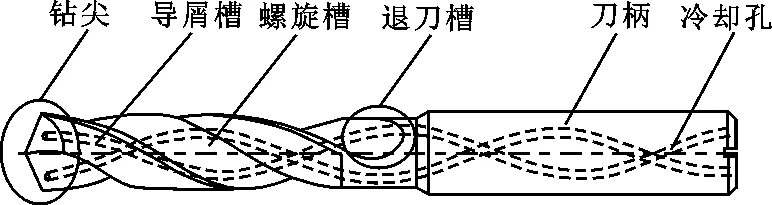
图1 硬质合金内冷钻头结构图

钻尖在钻削时需要承受绝大部分的推力和扭矩,它的结构在很大程度上影响钻头使用时工件的加工质量和钻头自身寿命,是其最重要的组成部分,如图2所示。与传统麻花钻的钻尖仅包含单曲面或双曲面组合不同,内冷钻头钻尖部分包含了多个曲面,包括前刀面、螺旋面后刀面、第一后刀面、第二后刀面、Gash面、螺旋面中间曲面等。冷却孔呈螺旋状延伸并且贯穿钻身,在钻尖部分与Gash面和第二后刀面相交。

退刀槽是螺旋槽面与钻头外表面的过渡曲面,主要用于加工时切屑的排出,可以提高加工孔表面质量以及加工效率。退刀槽的结构比较复杂,由多个曲面衔接而成,难以建立完整的数学模型。

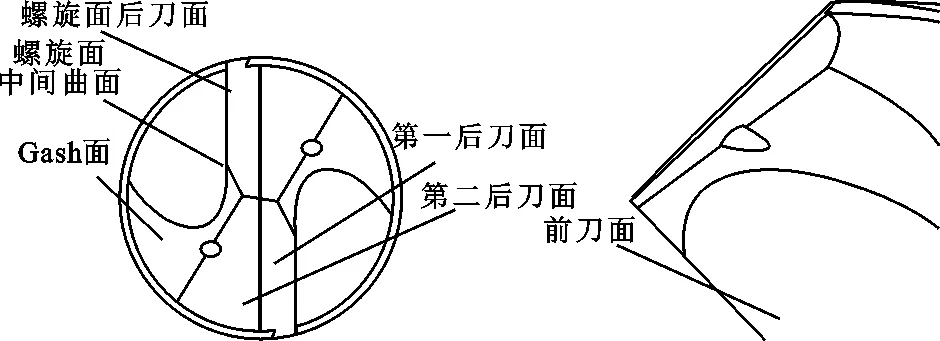
图2 钻尖结构图

2 硬质合金内冷钻头数学建模

2.1 螺旋槽截形的数学建模

螺旋槽是钻头十分重要的部分,它与后刀面的交线构成主切削刃,因此直接影响主切削刃的形状和钻头的切削性能。钻削时,螺旋槽提供排屑空间,它的形状和大小影响切屑排出的流畅性[12]。

用垂直于钻头轴线的平面截取硬质合金内冷钻头的工作部分,得到螺旋槽的周刃截形(略去冷却孔),如图3所示。图中AB段为钻刃曲线,BC段为槽底曲线,CD段为钻背曲线,DE段为刃带曲线,EF段为横刃曲线。表1给出了周刃截形已知参数。

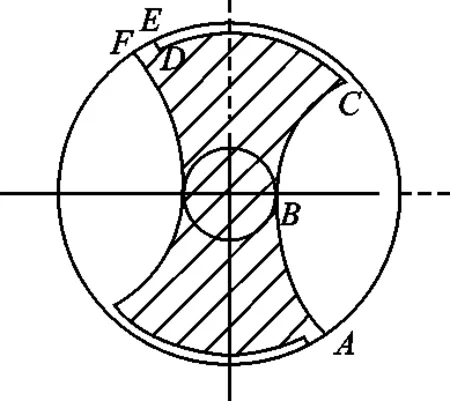
图3 螺旋槽周刃截形

周刃基本参数变量符号钻头半径R槽深C半钻芯厚度r螺旋角β钻尖顶角θ刃带高度c刃带宽度f

由文献[13]可得AB段钻刃曲线的参数方程为

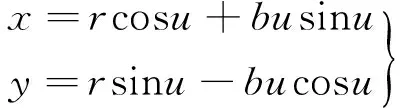
(1)

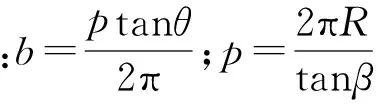
当u取(R2-r2)1/2/b时,代入式(1),可以得到A点的坐标A(xA,yA),同时易得B点的坐标B(xB,yB)=(r,0)。F点与A点关于坐标原点中心对称,可得F点的坐标F(-xA,-yA)。

BC段为槽底曲线,主要用于钻削过程中排出产生的废屑,对于精度的要求不高,可以为一段圆弧

(2)

CD段钻背曲线不涉及切削,也为一段圆弧,易得参数方程如下

(3)

联立式(2)、式(3),可得C点坐标C(xC,yC)

(4)

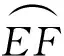
(5)

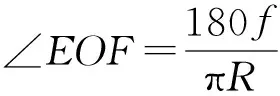
(6)

DE段长度为刃带高c,得到D点坐标D(xD,yD)为

(7)

至此,A～F点的坐标已全部求出。

2.2 螺旋线的数学建模

硬质合金内冷钻头的螺旋槽属于螺旋面结构,由母线和螺旋线构成:母线沿着螺旋线移动,生成刀具的螺旋面刀刃,即螺旋刃结构。螺旋线的示意图见图4。

内冷钻头螺旋刃为等螺旋角螺旋刃,因此等螺旋角圆柱螺旋线的表达式为

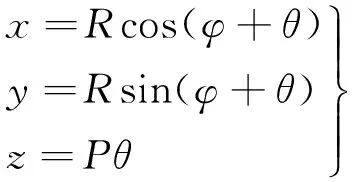
(8)

式中:φ为起始角;θ为变化系数;P为螺旋槽导程。

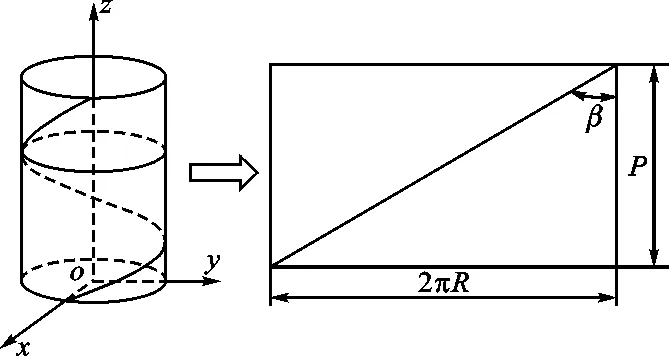
图4 螺旋线示意图

2.3 钻尖的数学建模

钻尖是钻头最重要的部分,该部分的设计需要保证端刃第一后角、第二后角等参数。其中,端刃前刀面在生成螺旋槽时已经形成,这里不再赘述。表2列出了钻尖数学建模中的已知参数。

表2 硬质合金内冷钻头钻尖部分参数表

2.3.1 第一后刀面的数学建模 如图5所示,建立相应坐标系。钻头的第一后刀面由两条在原点相交的直线确定,一条直线由端刃第一后角确定,另一条直线为钻尖的对称轴线。

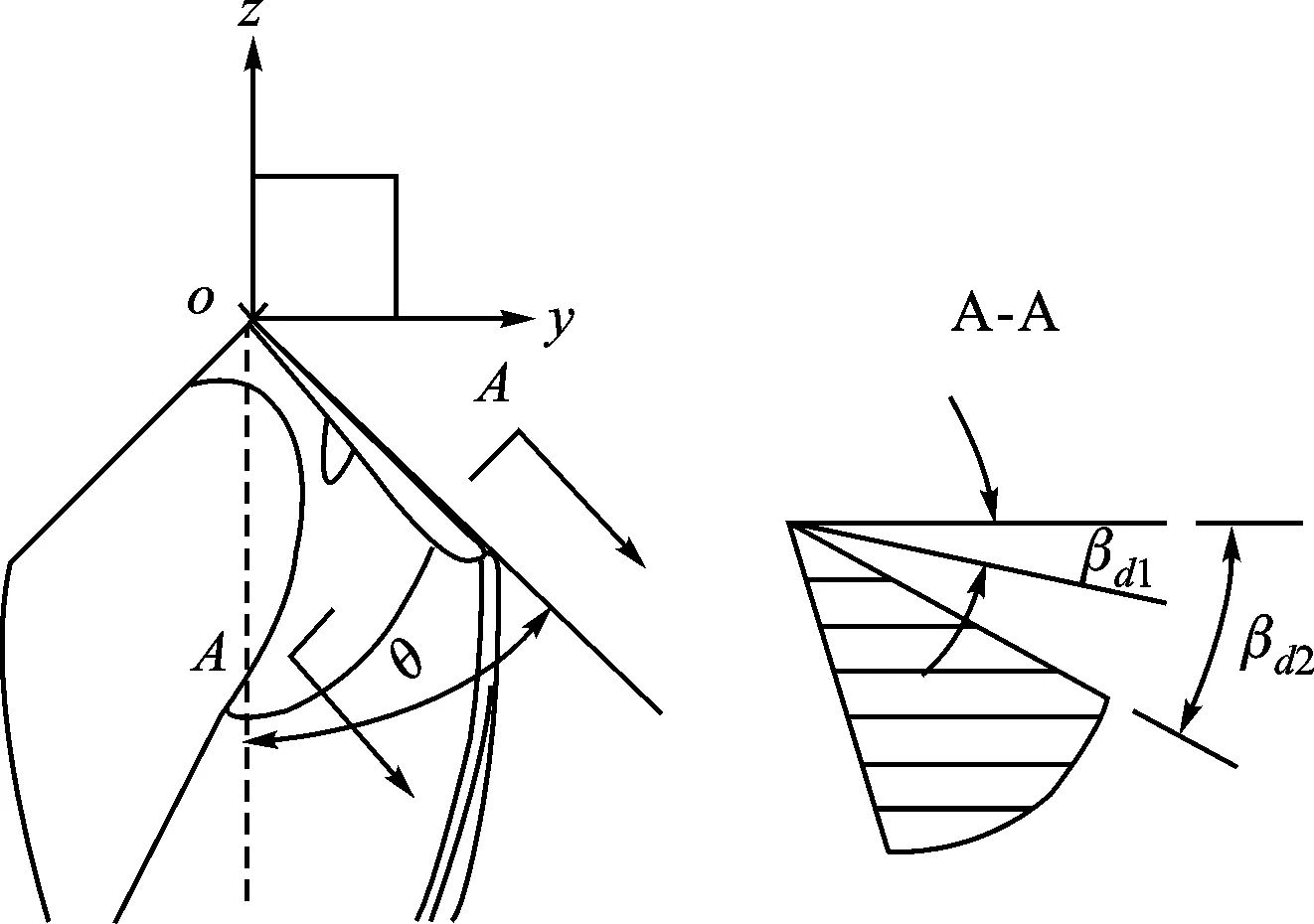
图5 端刃后角示意图

钻尖对称轴线在yoz平面内,由钻尖顶角确定,具体的参数表达式为

(9)

式中:l1为钻尖对称轴线的长度变化系数。

第一后刀面直线由端刃第一后角确定,其参数表达式为

(10)

式中:l2为第一后刀面直线的长度变化系数。

2.3.2 第二后刀面的数学建模 第二后刀面的建模方法和第一后刀面类似,由第二后刀面直线和第一后刀面直线确定。其中,第二后刀面直线的参数表达式为

(11)

式中:l3为第二后刀面直线的长度变化系数。

2.3.3 Gash面的数学建模 Gash面的建模需要建立相应的截面曲线,保证Gash面夹角的准确性。图6为截形曲线的示意图。

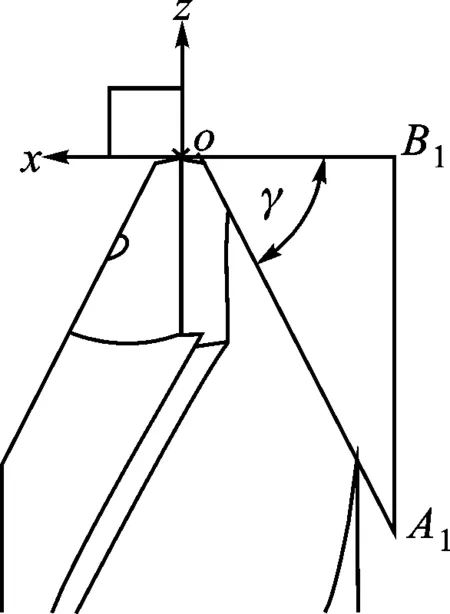
图6 Gash面截形示意图

为了保证在UG中进行布尔运算时截形能够完全和圆柱毛坯体进行修剪,将B1点的坐标设置为B1(xB1,yB1,zB1)=(-(R+1),0,0),根据几何关系,得到A1点的坐标A1(xA1,yA1,zA1)

(12)

3 三维参数化建模及其系统的实现

为了检验钻头数学模型的准确性,需要在三维软件中建立三维参数化模型进行验证。本文使用UG软件,应用其强大的造型功能,进行二次开发,建立硬质合金内冷钻头三维参数化模型,并成功搭建了硬质合金内冷钻头三维参数化设计系统。

3.1 硬质合金内冷钻头三维参数化建模

UG具有多种二次开发形式,包括UG/Open GRIP、UG/Open KF、UG/Open API等。综合比较各种开发方式的优劣,本文选取UG/Open API作为开发工具。为了保证钻头三维参数化模型的准确性,按照实际生产硬质合金内冷钻头的步骤结合数学模型进行参数化建模,具体建模流程见图7。

图7 硬质合金内冷钻头参数化建模流程图

根据式(1)～式(7)及A～F6个关键点的坐标,在UG中使用UF_CURVE_create_line、UF_CURVE_create_arc_point_point_radius等UG/Open API函数,并通过一定的坐标转换,生成周刃截形如图8所示。

在UG/Open API函数库中,没有直接可用的螺旋线生成函数,需要使用样条曲线进行拟合[14],运用UF_CURVE_create_spline_thru_pts函数进行操作。将周刃截形沿螺旋线进行扫掠(UF_MODL_create_sweep函数)得到螺旋槽片体,运用UF_MODL_trim_body函数与圆柱毛坯体进行修剪体操作,得到螺旋槽模型,如图9所示。

图8 1/2周刃截形 图9 螺旋槽模型

在钻头参数化建模过程中,退刀槽的建模是一大难点。退刀槽部分结构复杂,由曲面光滑过渡衔接而成,无法通过数学模型的方式进行三维建模。本文利用UG强大的曲面建模功能,使用桥接曲线(UF_CURVE_create_bridge_curve函数)、网格曲面(UF_MODL_create_curve_mesh函数)等操作,成功建立了退刀槽模型,如图10所示。

按式(10)、式(11)生成钻尖对称轴线和第一后刀面直线,并根据两条直线确定修剪平面,与圆柱毛坯体进行修剪体操作,得到第一后刀面模型。第二后刀面的建模过程和第一后刀面类似。根据图6和式(13),计算Gash面截形三点的坐标,生成截形,再沿钻头中心轴线垂直扫掠,与圆柱体进行修剪体操作,得到Gash面模型,最后生成的钻尖模型如图11所示。

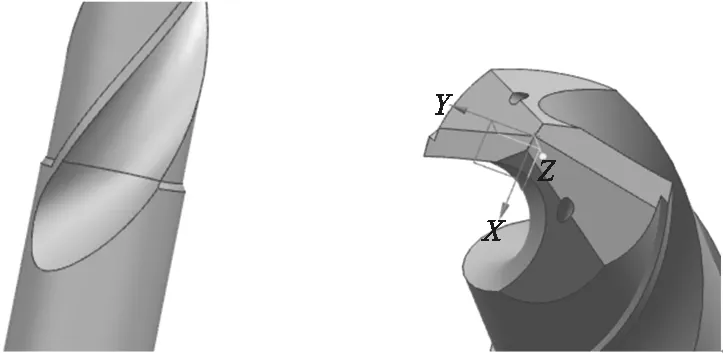
图10 退刀槽模型 图11 钻尖模型

3.2 硬质合金内冷钻头三维参数化设计系统的实现

为了实现交互式建模,在UG中建立硬质合金内冷钻头三维参数化设计系统,运用UG/Open二次开发技术,实现系统和UG软件的无缝连接。本文使用UG/Open MenuScript建立系统菜单栏,UG/Open UIStyler建立系统用户对话框,生成需要的菜单和对话框文件[15];在Visual Studio中使用UG/Open API函数库进行三维建模的程序编写,生成动态链接库文件[16],建立的系统如图12所示。

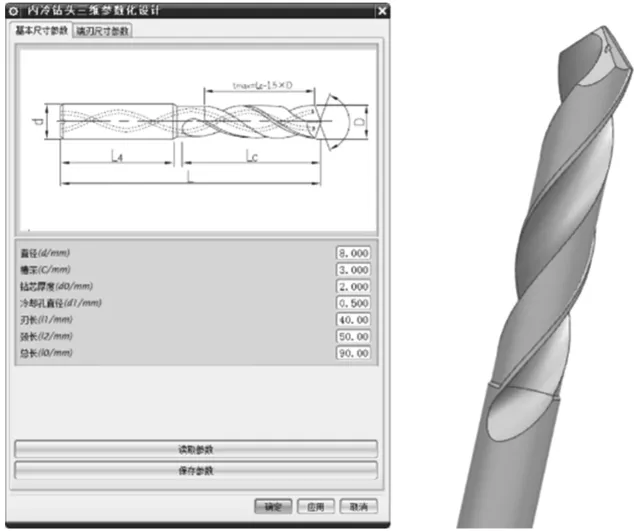
图12 系统对话框及运行结果

硬质合金内冷钻头三维参数化设计系统基于UG环境,运行方便,操作简单,在几何参数确定之后,可以快速地生成三维参数化模型,生成的模型满足螺旋角、端刃后角等参数要求,螺旋槽、退刀槽等部位连接光滑。

4 结束语

硬质合金内冷钻头的几何结构复杂,螺旋槽、钻尖等部位因为复杂曲线和复杂曲面的存在,使得精确建模的难度较大。本文对硬质合金内冷钻头的几何结构进行了分析,针对不同的部位进行数学建模,建立了螺旋槽、前刀面、后刀面、Gash面等部位的准确数学模型。借助UG中二次开发工具,建立了硬质合金内冷钻头三维参数化设计系统。经过测试,系统可以实现硬质合金内冷钻头的三维快速建模和精确建模,在保证设计精度的前提下,减少了设计时间,提高了设计效率。同时,本文研究的硬质合金内冷钻头已经在厦门金鹭公司投入生产,并应用于深孔加工和高硬度材料的加工。实际使用效果表明,硬质合金内冷钻头具有较好的钻削性能,优于一般的麻花钻头。但是,本文的研究仍存在不足之处,仅是针对硬质合金内冷钻头的几何结构进行了数学建模和三维参数化设计,没有完成进一步的切削仿真验证。鉴于目前内冷钻头普遍使用硬质合金,本文仅限于对硬质合金内冷钻头的一种刀具进行了数学建模和参数化建模,尚未扩展到其他特殊材料、特殊类型的内冷钻头。

[1] 赵彦玲, 车万博, 张朝军, 等. 内冷式麻花钻的参数化设计系统 [J]. 哈尔滨理工大学学报, 2011, 16(5): 34-38. ZHAO Yanling, CHE Wanbo, ZHANG Chaojun, et al. The parametric design system of inner cold twist drill [J]. Journal of Harbin University of Science and Technology, 2011, 16(5): 34-38.

[2] TSAI W D, WU S M. A mathematical model for drill point design and grinding [J]. Journal of Manufacturing Science and Engineering, 1979, 101(3): 333-340.

[3] 康德纯, ARMAREGO E J A. 麻花钻直线刃圆锥面刃磨法的数学建模 [J]. 大连理工大学学报, 1998, 38(3): 290-295. KANG Dechun, ARMAREGO E J A. Modelling of straight lipped conical point grinding method of twist drills [J]. Journal of Dalian University of Technology, 1998, 38(3): 290-295.

[4] PAUL A, KAPOOR S G, DEVOR R E. Chisel edge and cutting lip shape optimization for improved twist drill point design [J]. International Journal of Machine Tools and Manufacture, 2005, 45(4): 421-431.

[5] ABELE E, FUJARA M. Simulation-based twist drill design and geometry optimization [J]. CIRP Annals: Manufacturing Technology, 2010, 59(1): 145-150.

[6] CHEN W C. Applying the finite element method to drill design based on drill deformations [J]. Finite Elements in Analysis and Design, 1997, 26(1): 57-81.

[7] 李震. 内冷式麻花钻的参数化设计及有限元分析 [D]. 哈尔滨: 哈尔滨理工大学, 2012.

[8] 张义龙, 戴俊平, 武慧敏, 等. 基于Pro/E标准麻花钻实体模型的建立与测量 [J]. 工具技术, 2014, 48(10): 83-86. ZHANG Yilong, DAI Junping, WU Huimin, et al. Creation and measurement of three-dimensional entity model of standard twist drill based on Pro/E [J]. Tool Engineering, 2014, 48(10): 83-86.

[9] 荆浩旗, 白海清, 王春月, 等. 基于UG/Open GRIP的麻花钻参数化设计 [J]. 陕西理工学院学报: 自然科学版, 2014, 30(2): 10-14. JING Haoqi, BAI Haiqing, WANG Chunyue, et al. Parameter design of twist drill based on UG/Open GRIP [J]. Journal of Shaanxi University of Technology: Natural Science Edition, 2014, 30(2): 10-14.

[10]汪建鸿, 苟向锋. 标准麻花钻三维建模研究 [J]. 工具技术, 2015, 49(1): 33-36 WANG Jianhong, GOU Xiangfeng. 3D modeling studies of standards twist drill [J]. Tool Engineering, 2015, 49(1): 33-36.

[11]黎正科, 周志雄, 黑大全, 等. 深孔麻花钻三维参数化设计及其优化 [J]. 广西大学学报: 自然科学版, 2012, 37(5): 959-964. LI Zhengke, ZHOU Zhixiong, HEI Daquan, et al. 3D parametric design and optimization of twist deep hole drill [J]. Journal of Guangxi University: Natural Science Edition, 2012, 37(5): 959-964.

[12]倪志福, 陈壁光. 群钻: 倪志福钻头 [M]. 上海: 上海科学技术出版社, 1999: 9-20.

[13]刘世瑶, 耿芬然. 深孔麻花钻的端截面及螺旋面的加 工 [J]. 河北冶金, 2002(4): 27-31 LIU Shiyao, GENG Fenran. Working of end section shape and spiral surface of lengthened twist drills [J]. Hebei Metallurgy, 2002(4): 27-31.

[14]梁锡坤. B样条类曲线及其在曲线参数化中的应用 [J]. 计算机应用与软件, 2009, 26(4): 93-95. LIANG Xikun. Basic spline class curves and its application in parameterization of curves [J]. Computer Applications and Software, 2009, 26(4): 93-95.

[15]刘奇, 林岗. 基于Visual Studio 2010的UG二次开发研究 [J]. 自动化技术与应用, 2015(1): 40-41. LIU Qi, LIN Gang. Research of the secondary development of UG based on Visual Studio 2010 [J]. Techniques of Automation and Applications, 2015(1): 40-41.

[16]黄勇, 张博林, 薛运锋. UG二次开发与数据库应用基 础与典型范例 [M]. 北京: 电子工业出版社, 2008: 11-13.

(编辑 杜秀杰)

Three-Dimensional Parametric Modeling of Carbide Internal Cooling Aiguille

PAN Junhao,ZHUO Yong,LIAN Yunsong,ZHANG Xianglei

(School of Physics and Mechanical & Electrical Engineering, Xiamen University, Xiamen, Fujian 361005, China)

Aiming at complex structure and difficult parametric modeling of carbide internal cooling aiguille, a system for three-dimensional parametric design is developed in Unigraphics NX (UG). According to the design parameters, a mathematical model of the cross section of the end cutting edge is established. Then the cross section is swept along the helical curve to construct the helical groove model in UG. Differing from the point of the normal twist drill, which includes only single curved surface or double curved surface, the point of carbide internal cooling aiguille consists of several surfaces, like first flank face and second flank face, so their corresponding three-dimensional models are set up in UG with such parameters as first clearance angle, second clearance angle, and gash angle of this point. The detailed structure undercut is composed of a series of smooth surfaces, the undercut model can be created by a few UG operations, such as bridge curve, through curve mesh, etc. It is found that this three-dimensional model of carbide internal cooling aiguille is sufficiently precise, and the key parameters of carbide internal cooling aiguille, such as helix angle, clearance angle and Gash angle, can be described accurately with smooth transition at the undercut in the design system.

carbide internal cooling aiguille; mathematical model; parametric modeling; secondary development

2015-03-23。

潘俊浩(1992—),男,硕士生;卓勇(通信作者),男,副教授。

福建省产学研重大项目资助(2014H6025);福建省高端装备制造协同创新中心支持项目。

时间:2015-08-18

10.7652/xjtuxb201510008

TH128;TP391.7

A

0253-987X(2015)10-0048-06

网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150818.0922.002.html