均值张量成分分析及其在步态识别中的应用

贲晛烨,张鹏,孙成立,孟维晓

(1.南昌航空大学江西省图像处理与模式识别重点实验室, 330063, 南昌;2.山东大学信息科学与工程学院, 250100, 济南;3.哈尔滨工业大学电子与信息工程学院, 150080, 哈尔滨)



均值张量成分分析及其在步态识别中的应用

贲晛烨1,2,张鹏1,2,孙成立1,孟维晓3

(1.南昌航空大学江西省图像处理与模式识别重点实验室, 330063, 南昌;2.山东大学信息科学与工程学院, 250100, 济南;3.哈尔滨工业大学电子与信息工程学院, 150080, 哈尔滨)

针对步态识别中非负样本数据存在冗余,且未经中心化的多线性主成分分析保持聚类结构的特征向量不能对应最大特征值,导致识别效果下降的问题,提出一种保持原始张量数据均方长度的均值张量成分分析算法。该算法首先对原始样本任一模式下内积矩阵进行谱分解,计算该模式下相应的特征值和特征向量;其次,利用获得的特征值和特征向量计算均值向量,并对均值向量值进行降序排列,使较大均值向量值对应的特征向量构成该模式下的低维子空间;最后,将原始样本投影到该低维子空间,形成特征张量。与多线性主成分分析算法相比,该算法不需要对数据去中心化处理,而是保持非负数据均值向量最大均方欧几里德距离和方向。通过在USF步态数据库和TUM GAID步态数据库进行仿真实验,结果表明,经过均值张量成分分析预处理,在2个步态库上的平均识别率分别高达57%和75%,较其他传统方法的识别率有明显提高。

步态识别;均值张量成分分析;均方长度;均值向量

随着数据采集和存储能力的提升,大规模的高维数据每天都在各领域的实际应用中产生,因此各类用于数据挖掘的算法变得越来越重要。高阶张量数据,如步态识别中的灰度图像序列可用于身份识别[1-2]。由于张量数据的高相关性,因此可假设其具有高约束性,并可以映射到一个子空间中,此时的特征提取就是将高维数据转换为低维的形式,因为没有破坏数据的结构,所以可保留大部分几何结构信息,而张量子空间学习主要集中于高阶张量数据的维数约简上。

对张量的维数约简方法主要分成2大类。一类是基于张量-张量投影(tensor-to-tensor projection,TTP),即从高维张量直接投影到低维同阶张量,一个N阶投影使用N个投影矩阵,它可以通过N步来实现,每步来执行一个张量矩阵乘法。这N步是可交换的,这种投影是子空间学习中高阶奇异值分解的一个延伸。另一类是基于张量-向量投影(tensor-to-vector projection,TVP),即一个高维张量到一个低维向量的直接投影,也叫做一阶投影。从一个张量到一个标量的投影是一个基本多重线性投影(elementary multilinear projection,EMP)的映射。在基本多重线性投影中,一个张量通过N个单位投影向量投影成一个点。因此,一个张量到一个在P维向量空间的向量的TVP包括P个基本多重线性投影,这种投影是标准分解的一个延伸。

典型的TTP算法有多重线性主成分分析(multilinear principal component analysis,MPCA)[3]和多重线性判别分析(multilinear discriminant analysis,MLDA)。MPCA属于非监督的全局方法,MLDA属于监督的全局方法。现有的MLDA方法比较典型的是张量表达的判别分析(discriminant analysis with tensor representation,DATER)[4]和广义张量判别分析(general tensor discriminant analysis,GTDA)[5]。DATER与GTDA的优化准则函数不同,DATER的优化准为最大化散布之商,它的缺点就是迭代求解不收敛,GTDA能保证迭代求解的收敛性,其优化的是散布之差最大化,它的缺点是散布的权参数很难取,对参数设置敏感。典型的TVP算法有:不相关多线性主成分分析(uncorrelated MPCA,UMPCA)[6]和不相关多线性判别分析(uncorrelated MLDA,UMLDA)[7]。近几年,Wang等人把一幅彩色图像看作为一个三阶张量,还提出了一种张量判别颜色空间模型[8]。Liu等人给出了张量数据维数约简的一般框架,提出一种多重线性局部保留的最大信息嵌入算法[9]。本文拟借鉴均值向量成分分析算法[10]和MPCA[3]的思想,保留原始张量数据的均方长度,提出均值张量成分分析(mean tensor component analysis,MTCA)算法,并通过保持非负数据均值向量最大均方欧几里得距离和方向来求得投影变换矩阵。在USF和TUM GAID等步态数据库上进行了实验,获得了令人满意的识别效果。

1 均值张量成分分析

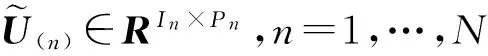
(1)

式中:×n表示张量乘积;⊗表示克罗内克积;Yj∈RP1⊗RP2⊗…⊗RPN,j=1,…,M。

令Xj(n)表示第j个样本的n模式矩阵,则

(2)

(3)

因此,原始张量数据的均方长度,即‖m‖2可以定义为

(4)

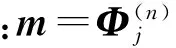
(5)

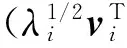
2 均值张量成分分析算法

2.1 算法步骤

MTCA的复杂度与MPCA相当,都在于对特征值、特征向量的计算,但是MTCA不需要对数据进行去中心化处理,而MPCA需要计算每个模式下的去中心化后的协方差矩阵的特征值和特征向量,投影变换矩阵由较大的特征值对应的特征向量组成;MTCA可能与较小的特征值有关,它是通过计算Φ(n)的前Pn个较大的均值向量值对应的均值向量来组成投影矩阵。MTCA算法步骤如下。

步骤4 对于n模式,计算Φ(n),并计算它的特征值和特征向量λin、uin,in=1,…,In。

步骤6 重复步骤4、步骤5,直到遍历所有模式。

步骤7 重新计算{Yj,j=1,…,M}和ΨYk。当ΨYk-ΨYk-1<η时,跳出循环,转到步骤8,否则返回步骤4。

2.2 收敛性分析

MTCA算法的投影矩阵初始化、优化和投影过程采用2.1节所述算法步骤,张量数据集选为USF步态数据库[11]中的Gallery数据集,第k次迭代后的投影后的散布记为ΨYk。图1所示是MTCA与MPCA算法的收敛性测试情况,由图1可知,两种算法都只迭代了一次就已经收敛了。在USF步态数据库的测试集A上还比较了MTCA和MPCA算法随迭代次数增加的识别率情况,如表1所示。因此在后续的实验中,MTCA和MPCA算法的迭代次数均设定为1次。

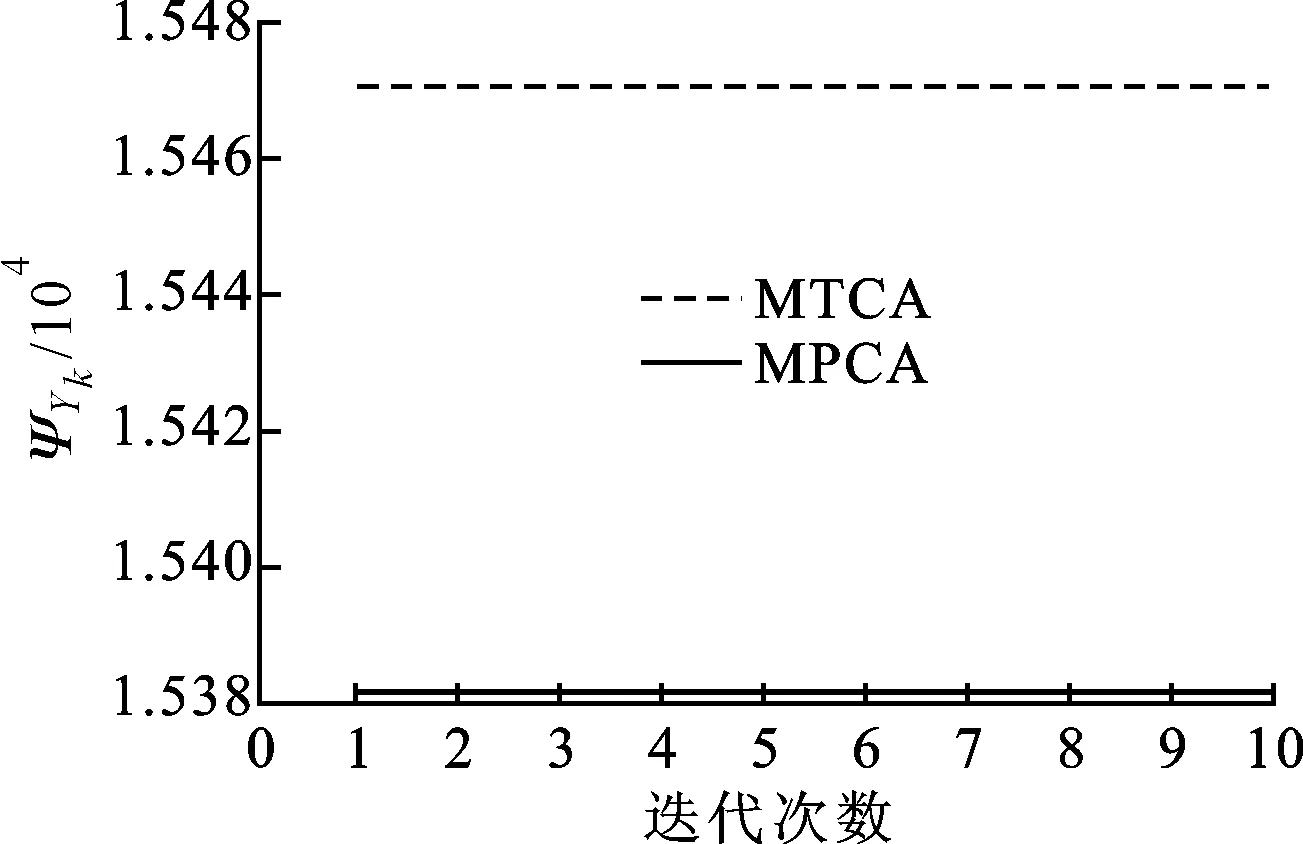
图1 2种算法的收敛性测试

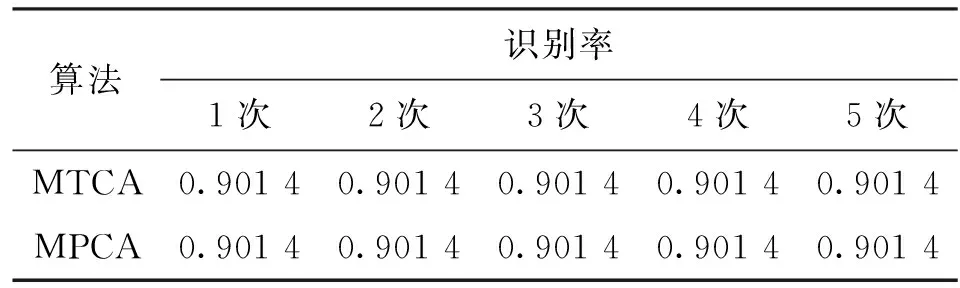
算法识别率1次2次3次4次5次MTCA0.90140.90140.90140.90140.9014MPCA0.90140.90140.90140.90140.9014

3 实验结果与分析

为了评估各种特征提取方法的效果,分类器均采用最简单且有效的最近邻分类器(1-NN),距离度量方式为改进的角度距离(modified angle distance,MAD)[7]。为了表示方便,本文中将MPCA与LDA算法级联命名为多线性主成分判别分析(multilinear principal component discriminant analysis,MPCDA),将MTCA与LDA命名为均值张量成分判别分析(mean tensor component discriminant analysis,MTCDA),将GTDA与MTCA算法级联命名为广义张量判别均值成分分析(general tensor discriminant mean component analysis,GTDMCA),将GTDA与MTCA以及LDA级联算法命名为广义均值张量判别分析(general tensor mean discriminant analysis,GTMDA)。

3.1 USF步态数据库实验

USF步态数据库的数据集由74个对象的452个行走图像序列组成,其中用于训练的一组(Gallery)包含71个图像序列,用于测试的共有7组,这些图像序列如图2所示。

对于每个对象,共有如下几组的变化因素:视角(左L或右R)、鞋型(A或B)、步行路面(草地G或混凝土地面C),具体可参考表2。

(a)测试组1 (b)测试组2

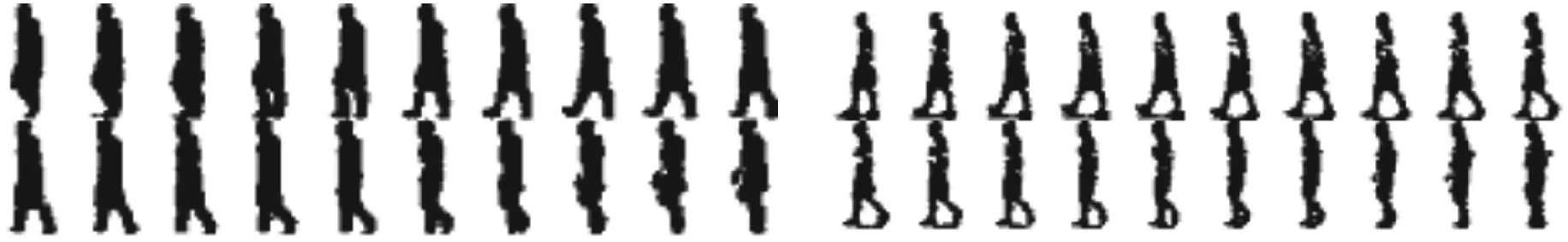
(c)测试组3 (d)测试组4

(e)测试组5 (f)测试组6

(g)测试组7图2 USF步态数据库测试集

测试组测试组内变化因素测试对象数训练组与测试组间不同点1(G,A,L)71视角2(G,B,R)41鞋型3(G,B,L)41视角、鞋型4(C,A,R)70路面5(C,B,R)44路面、鞋型6(C,A,L)70路面、视角7(C,B,L)44路面、鞋型、视角

将原始的步态图像尺寸从128×64像素下采样到32×22像素,在测试组1～7上测试MTCA、MTCDA、GTMDA等方法的识别率,其中GTDA算法的调谐因子ζ=0.1,并与Baseline[11]、PCA、LDA、LPP、均值向量成分分析(MVCA)[10]、MPCA[3]、MPCDA[3]和GTDA[5]相比较,实验结果如图3所示。由图3可以看出:MTCA算法的平均识别率略高于MPCA的平均识别率;通过级联GTDA、MTCA和LDA所构成的算法可以获得最佳的平均识别率57%;MTCDA算法可以获得平均识别率是54%。本文进一步采用累积匹配得分(cumulative match score,CMS)来评估前述的这些方法,CMS描述的是期望正确的匹配条件下必须搜索匹配前R(R为排序结果值,如R=1表示相似度最近的1年识别结果,R=5表示相似度最近的5个识别结果)个训练样本,图4所示是R=5下的各种方法的CMS结果,可以看出GTMDA方法的平均CMS仍然是最高的,高达79%。

对比图3和图4的测试组1～3的实验结果,可以看出:各个方法在测试组1～3上都获得了很好的识别效果,这说明视角和鞋型2种变化因素对识别影响不大。与测试组1～3相比,测试组4～7的识别效果明显变差,因此可以看出,路面类型对识别影响要大过视角和鞋型,当这3种因素同时都发生变化时,识别效果是最差的,而且GTMDA较其他方法在测试组4～7上更可看出明显的优势,这是因为GTDA和MTCA算法相当于2步预处理,预处理时既提取张量数据的鉴别特征,又同时保留输入张量数据的均值向量的均方长度,之后将张量向量化后再进行线性的判别分析较将张量向量化直接LDA的分类效果要好。

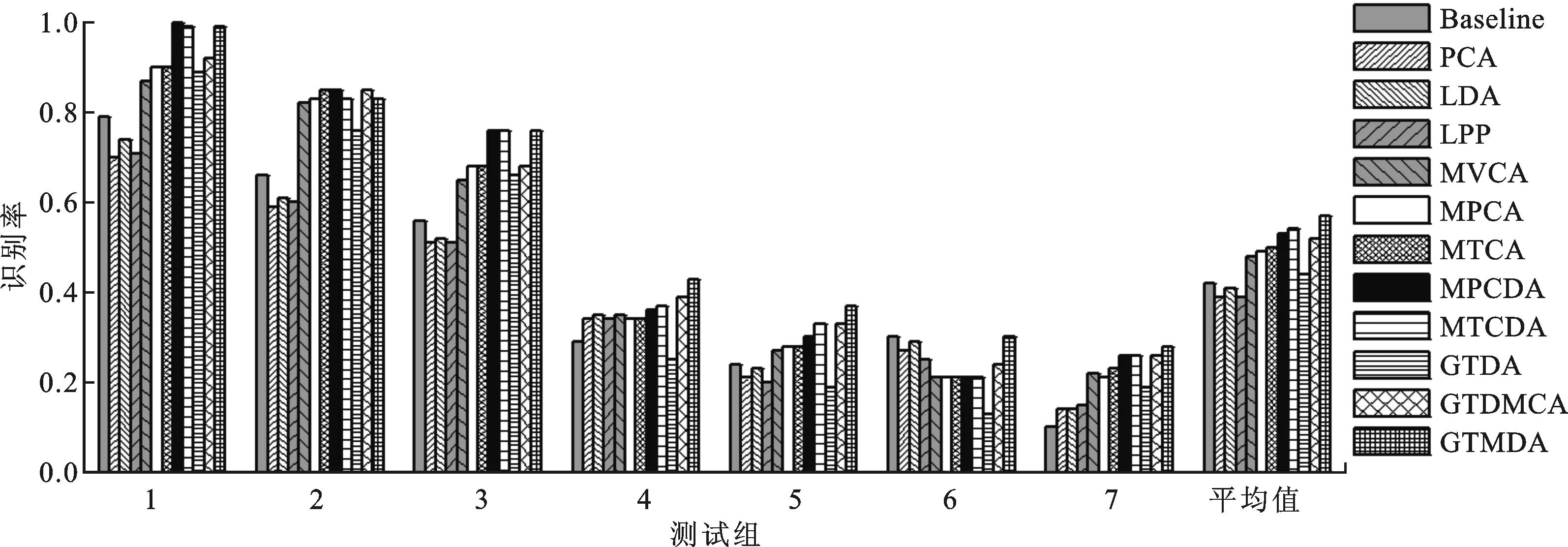
图3 USF数据库下的识别率结果

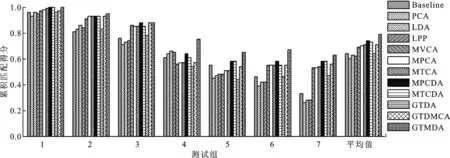
图4 USF数据库下的累积匹配得分(R=5)

3.2 TUM GAID深度步态库实验

TUM GAID数据库[12]是一个集音频、图像和深度信息的步态库。全库共有305个人的3 370个步态序列,每人有6段正常的步态序列,2段穿着软底鞋,2段背包(大约5 kg)的步态序列,覆盖各个年龄、性别以及身高类型。图5所示为该库正常步态(normal)、穿软底鞋步态(shoes)和背包步态(bag)序列。

(a)正常步态

(b)软底鞋步态 (c)背包步态 图5 TUM GAID步态序列

实验时将每个人的前4段正常步态序列进行训练,第1组实验采用每个人的后2段正常步态序列进行测试,第2组实验采用软底鞋条件下的步态序列进行测试,第3组实验采用背包条件下的步态序列进行测试。GTDA的调谐因子仍取ζ=0.1。图6和图7所示分别为MTCA、MTCDA、GTMDA与GEI、PCA、LDA、LPP、MVCA、MPCA、

MPCDA和

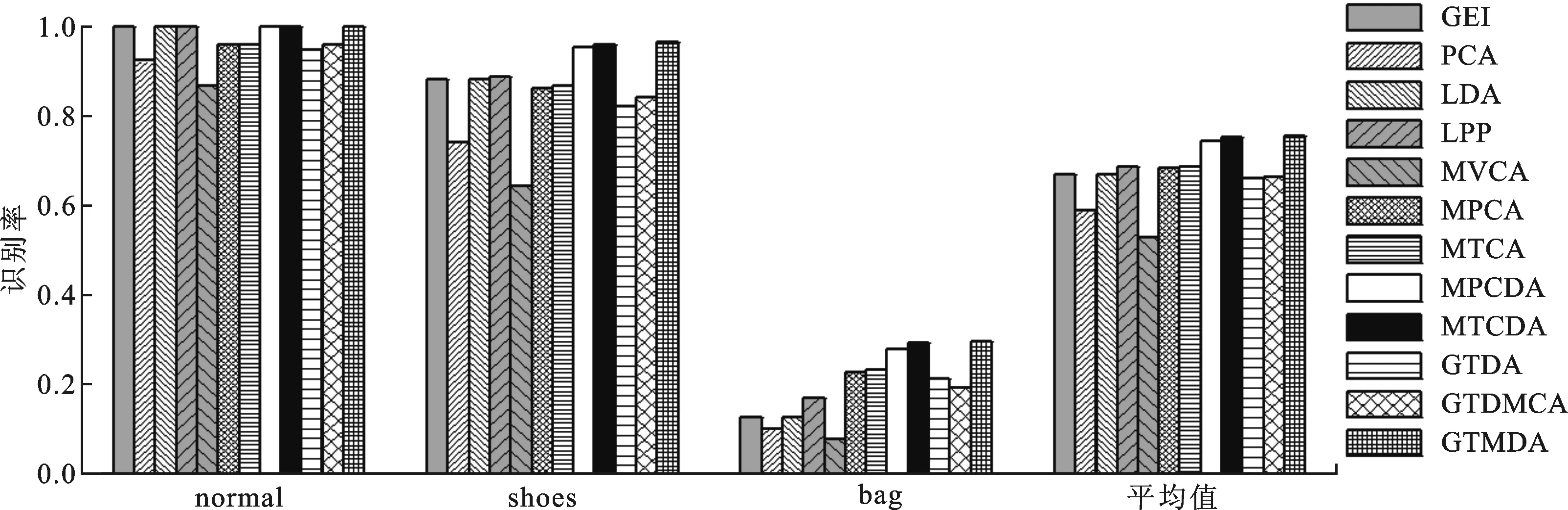
图6 TUM GAID数据库下的识别率结果

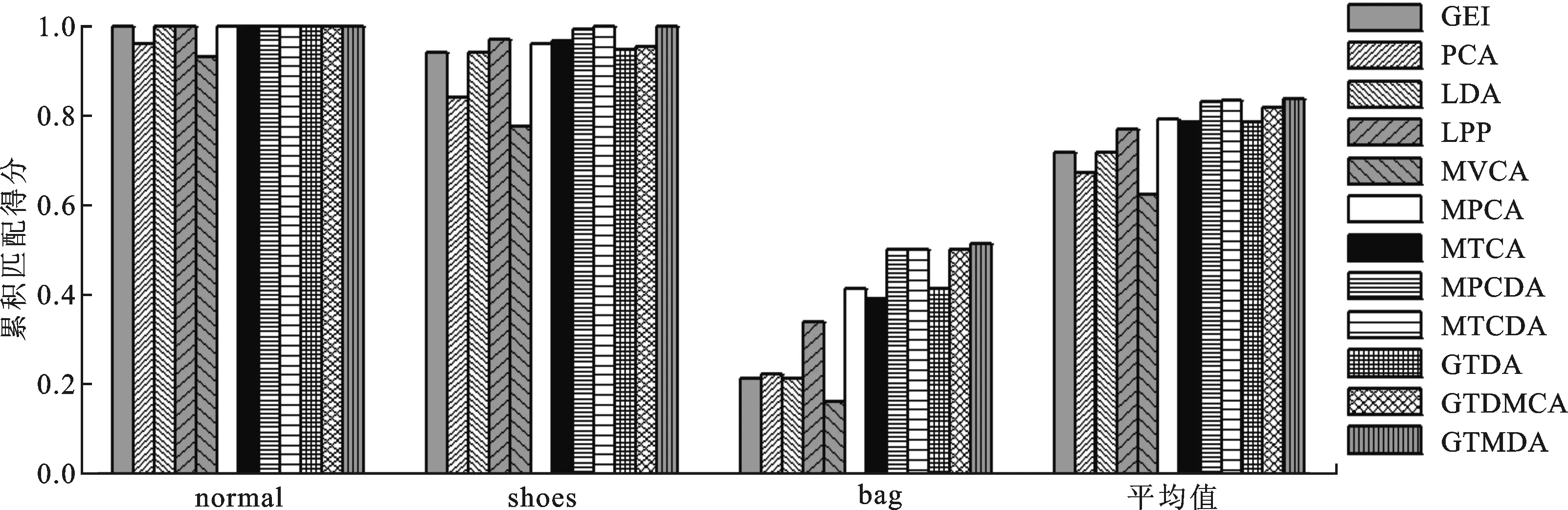
图7 TUM GAID数据库下的累积匹配得分(R=5)

GTDA算法在平均识别率、累积匹配得分(R=5)的对比结果,可以看出:GTMDA算法在3组实验下的平均识别率为0.753 3,略高于MTCDA(平均识别率为0.751 1);GTMDA算法在R=5下的平均CMS为0.837 7。还可以看出:背包对步态识别的影响比软底鞋的影响要大很多,在跨因素下的步态识别问题上,GTMDA算法体现出更明显的优势。

3.3 算法运行时间比较结果

实验环境为CPU:Intel®CoreTM2 Duo T5870@2.00 GHz,内存为2.00 GB的PC机。表3所示为各种算法在USF步态数据库上的训练时间与数据集1～7的平均测试时间。表4所示为各种算法在TUM GAID步态数据库上3种测试条件下的平均训练时间与平均测试时间。由实验结果可以看出:多线性子空间学习的各种算法,如MPCA、MTCA、MPCDA、MTCDA、GTDA、GTDMCA和GTMDA的训练时间和测试时间都要比线性子空间学习算法(PCA、LDA、LPP、MVCA)的长。由于USF步态数据库的训练样本集较小,因此,各种算法的训练时间都较短。同样地,测试样本集较大时,如TUM GAID步态数据库,各种算法的测试时间都较测试样本集小的库要长。

表3 各算法对USF步态数据库的运行时间

表4 各算法对TUM GAID步态数据库的运行时间

4 结束语

本文提出了一种均值张量成分分析算法,它是通过保持非负数据均值向量最大均方欧几里得距离和方向来求得投影变换矩阵的,该算法具有很快的收敛速度,跟MPCA算法的复杂度相当。与MPCA算法相比较,本文算法不需要对数据去中心化处理,投影变换矩阵是由对应较大均值向量值的均值向量组成。在USF步态数据库和TUM GAID深度步态库上进行实验验证得出:本文所提算法具有较好的步态识别效果,但路面、鞋型、视角、背包或其联合因素对步态识别的性能影响很大,因此,下一步的工作重点将耦合度量学习理论[13-14]和张量子空间学习理论,以实现跨因素下的鲁棒步态识别。

[1] 陈实, 高有行. 一种轮廓变化图像小波矩的步态识别 [J]. 西安交通大学学报, 2009, 43(1): 90-94. CHEN Shi, GAO Youxing. Gait recognition with wavelet moments of silhouette change images [J]. Journal of Xi’an Jiaotong University, 2009, 43(1): 90-94.

[2] 贲晛烨, 徐森, 王科俊. 行人步态的特征表达及识别综述 [J]. 模式识别与人工智能, 2012, 25(1): 71-81. BEN Xianye, XU Sen, WANG Kejun. Review on pedestrian gait feature expression and recognition [J]. Pattern Recognition & Artificial Intelligence, 2012, 25(1): 71-81.

[3] LU H, PLATANIOTIS K N, VENETSANOPOULOS A N. MPCA: multi-linear principal component analysis of tensor objects [J]. IEEE Transactions on Neural Networks, 2008, 19(1): 18-39.

[4] YAN S, XU D, YANG Q, et al. Discriminant analysis with tensor representation [C]∥IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005. Piscataway, NJ, USA: IEEE, 2005: 526-532.

[5] TAO D, LI X, WU X, et al. General tensor discriminant analysis and Gabor features for gait recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(10): 1700-1715.

[6] LU H, PLATANIOTIS K N, VENETSANOPOULOS A N. Uncorrelated multilinear principal component analysis for unsupervised multilinear subspace learning [J]. IEEE Transactions on Neural Networks, 2009, 20(11): 1820-1836.

[7] LU H, PLATANIOTIS K N, VENETSANOPOULOS A N. Uncorrelated multilinear discriminant analysis with regularization and aggregation for tensor object recognition [J]. IEEE Transactions on Neural Networks, 2009, 20(1): 103-123.

[8] WANG S, YANG J, ZHANG N, et al. Tensor discriminant color space for face recognition [J]. IEEE Transactions on Image Processing, 2011, 20(9): 2490 -2501.

[9] LIU Y, LIU Y, CHAN K C C. Tensor distance based multilinear locality-preserved maximum information embedding [J]. IEEE Transactions on Neural Networks, 2010, 21(11): 1848-1854.

[10]JENSSEN R. Mean vector component analysis for visualization and clustering of nonnegative data [J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(10): 1553-1564.

[11]SARKAR S, PHILLIPS P, LIU Z, et al. The human ID gait challenge problem: data sets, performance and analysis [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(2): 162-177.

[12]HOFMANN M, GEIGER J, BACHMANN S, et al. The TUM gait from audio, image and depth (GAID) database: multimodal recognition of subjects and traits [J]. Journal of Visual Communication and Image Representation, 2014, 25(1): 195-206.

[13]BEN X, MENG W, YAN R, et al. Kernel coupled distance metric learning for gait recognition and face recognition [J]. Neurocomputing, 2013, 120: 577-589.

[14]BEN X, MENG W, YAN R, et al. An improved biometrics technique based on metric learning approach [J]. Neurocomputing, 2012, 97: 44-51.

[本刊相关文献链接]

彭亚丽,刘侍刚,裘国永.一种线性迭代非刚体射影重建方法.2015,49(1):102-106.[doi:10.7652/xjtuxb201501017]

周远,周玉生,刘权,等.一种适用于图像拼接的DSIFT算法研究.2015,49(9):84-90.[doi:10.7652/xjtuxb201509015]

毛彦斌,张选平,杨晓刚.伪DNA密码图像加密算法研究.2015,49(9):91-98.[doi:10.7652/xjtuxb201509016]

刘凯,张立民,孙永威,等.利用深度玻尔兹曼机与典型相关分析的自动图像标注算法.2015,49(6):33-38.[doi:10.7652/xjtuxb201506006]

吴一全,孟天亮,吴诗婳.人工蜂群优化的非下采样Shearlet域引导滤波图像增强.2015,49(6):39-45.[doi:10.7652/xjtuxb201506007]

唐晓庆,范赐恩,刘鑫.基于边缘保持滤波的单幅图像快速去雾.2015,49(3):143-150.[doi:10.7652/xjtuxb201503022]

杨晔,潘希德,庄健.一种针对超声检测图像的自适应阈值设置方法.2015,49(1):127-132.[doi:10.7652/xjtuxb201501 021]

侯兴松,张兰.方向提升小波变换域稀疏滤波的自然图像贝叶斯压缩感知.2014,48(10):15-21.[doi:10.7652/xjtuxb 201410003]

李博,冯松,毛军红.在线图像可视铁谱LED阵列反射光源设计与实现.2014,48(10):29-34.[doi:10.7652/xjtuxb2014 10005]

袁飞,朱利,张磊.利用超图图割的图像共分割算法.2014,48(02):20-24.[doi:10.7652/xjtuxb201402004]

符均,牟轩沁,季文博.亮色分离的饱和图像校正方法.2014,48(10):101-107.[doi:10.7652/xjtuxb201410016]

储颖,牟轩沁,洪伟.采用形状一致性特征的盲图像质量评价方法.2014,48(8):12-17.[doi:10.7652/xjtuxb201408003]

夏虎,庄健,于德弘.面向高维特征故障数据的进化软子空间聚类算法.2013,47(5):115-120.[doi:10.7652/xjtuxb201305 021]

刘剑毅,何苗,马瑶,等.面向人脸光照合成的光照参数精确估计算法.2013,47(6):18-24.[doi:10.7652/xjtuxb201306 004]

李玉花,齐春.利用位置字典对的人脸图像超分辨率方法.2012,46(6):7-11.[doi:10.7652/xjtuxb201206002]

蒋舒卉,钱学明.一种重要区域重采样的人脸检索方法.2012,46(2):119-123.[doi:10.7652/xjtuxb201202020]

岳桂华,滕奇志,何小海,等.岩心三维图像修复算法.2014,48(9):37-42.[doi:10.7652/xjtuxb201409007]

海涛,丛爽,鲍远律.彩色城市栅格地图道路网络自动获取方法.2011,45(12):16-21.[doi:10.7652/xjtuxb201112004]

罗涛,牟轩沁.一种胸部X射线摄影图像中结节检测的多尺度匹配滤波器.2011,45(4):30-35.[doi:10.7652/xjtuxb 201104006]

杨宏晖,戴健,孙进才,等.用于水声目标识别的自适应免疫特征选择算法.2011,45(12):28-32.[doi:10.7652/xjtuxb 201112006]

赵海峰,姚丽莎,罗斌.改进的人工鱼群算法和Powell法结合的医学图像配准.2011,45(4):46-52.[doi:10.7652/xjtuxb201104009]

余旺盛,侯志强,王朝英.频谱包络滤波器及其应用.2010,44(8):48-52.[doi:10.7652/xjtuxb201008010]

(编辑 刘杨)

A Mean Tensor Component Analysis and Its Application in Gait Recognition

BEN Xianye1,2,ZHANG Peng1,2,SUN Chengli1,MENG Weixiao3

(1. Key Laboratory of Jiangxi Province for Image Processing and Pattern Recognition, Nanchang Hangkong University,Nanchang 330063, China; 2. School of Information Science and Engineering, Shandong University, Jinan 250100, China;3. School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150080, China)

A novel algorithm named mean tensor component analysis (MTCA) is proposed to solve the low recognition accuracy problem that is caused by redundancy in nonnegative sample data and non-corresponding relationship that the eigenvector which preserves clustering structure in uncentered multilinear principal component analysis (MPCA) does not correspond to the maximum eigenvalues. The algorithm reserves the squared length of original tensor data. Spectral decomposition is performed to the inner-product matrix of original samples in any mode to obtain eigenvalues and corresponding eigenvectors. Then, mean value and mean vector are calculated from the eigenvalues and eigenvectors, and the values of the mean vector are sorted in a descending order so that a subspace is formed from the eigenvectors corresponding to first several largest values of the mean vector. Then a feature tensor is acquired by mapping the original sample to the subspace. A comparison to MPCA shows that the proposed algorithm preserves the squared length and the direction of mean vector of non-negative data without needs of decentralized processing to the data. Experiments on USF and TUM GAID gait databases show that the MTCA algorithm achieves average recognition rate 57% and 75%, respectively, and that the rates are obviously higher than the recognition rates of some conventional methods.

gait recognition; mean tensor component analysis; squared length; mean vector

2015-03-20。

贲晛烨(1983—),女,副教授。

国家自然科学基金资助项目(61201370,61362031,61571275);教育部高等学校博士学科点专项科研基金资助项目(20120131120030);山东大学青年学者未来计划资助项目(2015WLJH39)。

时间:2015-10-03

10.7652/xjtuxb201512007

TP391.41

A

0253-987X(2015)12-0040-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151003.1921.012.html