基于Zobory模型的机车车轮磨耗研究*

TAO VAN CHIEN(越南), 李 芾, 丁军君， 戚 壮

(西南交通大学 机械工程学院， 四川成都 610031)



基于Zobory模型的机车车轮磨耗研究*

TAO VAN CHIEN(越南), 李 芾, 丁军君， 戚 壮

(西南交通大学 机械工程学院， 四川成都 610031)

以D20E型内燃机车为例，采用SIMPACK软件建立了该型机车动力学模型，并根据越南干线实际线路建立线路模型。根据FASTSIM算法与Zobory磨耗预测模型，对机车车轮踏面磨耗的分布和发展情况进行仿真计算，并与现场测量结果进行比较。结果表明：车轮踏面上(-50～ 45 mm)区间是发生磨耗的主要范围，在轮缘根部处(-37～ -26 mm)范围内磨耗最大；随着运行距离的增加，车轮轮缘根部处的磨耗更加明显，踏面磨耗发展规律基本相同；踏面磨耗量的预测结果较实际测量结果低。

车辆工程； 机车； 磨耗模型； 动力学仿真； FASTSIM

机车车轮磨耗是一个非常复杂的问题及重要研究的领域。自19世纪机车车轮磨耗问题被提出以来，各国科学家用很多方法与途径在机车车轮磨耗开展了大量的研究，主要集中在轮轨滚动基础理论，磨耗的试验和仿真，磨耗的滚动接触疲劳的耦合关系上面。Olofsson 等基于Archard磨耗模型对边界润滑条件下的球形轴承由于轻微磨耗引起的形状改变过程进行仿真，仿真结果与实测结果吻合较好[1-2]; Ansary 等对机车轮缘厚度进行测量，然后对每个轮缘厚度下的磨耗率进行计算，结果表明轮缘厚度越小，磨耗率越大[2-3]；Zobory根据能量流密度发展了车轮踏面磨耗预测模型[4]。丁军君等基于半赫兹接触，赫兹接触和Kalker完全理论程序CONTACT 分别计算轮轨接触应力和接触形状，并计算车轮磨耗深度在踏面上的分布[5]。通过多年的研究，现在轮轨滚动接触理论越来越完善，并成为铁路机车车辆动力学的主流方向之一。

目前越南铁路的机车都从国外进口，机车在越南铁路实际运用条件有差别，所以车轮在两次旋修之间的磨耗与初始设计值有所不同。若车轮在实际中磨耗过大，则会影响行车安全；但若车轮在旋修周期间磨耗不足，则会增加线路和机车车辆的检修维护工作量。因此，对机车车轮磨耗进行研究是非常必要的。以D20E型内燃机车为例，将Zobory车轮磨耗仿真模型与FASTSIM算法应用于车轮磨耗仿真研究，编写了相应的计算程序，并确定了车轮踏面磨耗发展情况与磨耗分布。

1 车轮磨耗计算模型

计算机车车轮磨耗模型包括机车动力学仿真模型，

轮轨接触分析与车轮磨耗预测模型。通过机车动力学计算模型得出了轮轨接触的位置，轮轨法向力，轮轨蠕滑力。基于轮轨接触模型得到接触区域上每个单元格的滑动量分布，蠕滑率分布，切向应力分布等参数。根据磨耗预测模型计算每个单元格的磨耗量，然后进行累加得到踏面的磨耗深度。机车在实际运行，车轮踏面的磨耗是连续的过程，而在仿真中不能对车轮踏面实时更新，因此只能在车轮磨耗到一定限值时再更新。对不同更新磨耗深度的效果对比分析，本文采用0.1 mm磨耗量作为车轮型面更新的条件。更新后，采用新的踏面形状在重复计算。整个仿真计算过程如图1所示。

图1 车轮磨耗仿真计算过程

1.1 机车—轨道系统动力学模型

以D20E型内燃机车为例，采用SIMPACK软件建立了该型机车动力学模型如图2所示。模型包括车体，轮轨，两个构架，钢轨，道床，轨枕以及弹簧，阻尼等元件构成，该型机车的主要技术参数如表1所示。车轮初始型面为实测的ML20型踏面，轨道采用越南P43的钢轨，1∶20轨底坡，轨距为1 000 mm，参数见文献[6]。模型中假设轮对，构架和车体均为刚体，并忽略钢轨的弹性变形。

图2 D20E型机车动力学模型

技术参数数值柴油机功率/kW1492机车计算整备质量/t81机车最大速度/(km·h-1)120两转向架中心距/mm10300轴距/mm1650轮径/mm1016轴重/t13．5转向架自重/t14．53每轴簧下质量/t2．647一系悬挂纵向刚度/(kN·m-1)4．21×104一系悬挂横向刚度/(kN·m-1)2．16×103一系悬挂垂向刚度/(kN·m-1)5．74×102二系悬挂纵向刚度/(kN·m-1)2．28×102二系悬挂横向刚度/(kN·m-1)2．28×102二系悬挂垂向刚度/(kN·m-1)6．82×103一系垂向油压减振器阻尼系数/(kN·s·m-1)60二系横向油压减振器阻尼系数/(kN·s·m-1)60二系抗蛇行减振器阻尼系数/(kN·s·m-1)60左右滚动圆距离/mm1070通过最小半径曲线/m70

在动力学模型仿真中选用美国轨道不平顺五级线路谱进行计算。

线路以越南的岘港—西贡线路为例，根据越南实际线路的直线和曲线比例进行建立线路模型。岘港—西贡线路总长935 km，共有曲线738个，曲线总长244.31 km，占线路总长的26.1%，岘港—西贡线路上不同曲线半径及对应长度如表2所示[6]

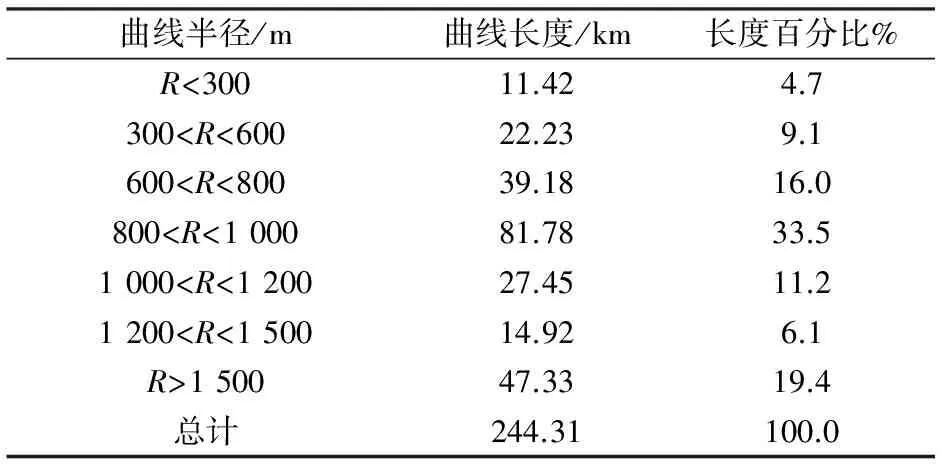
表2 岘港—西贡线路不同曲线半径及对应长度

1.2 轮轨滚动接触理论

在车轮磨耗仿真分析中，轮轨滚动接触模型对计算速度和精度的影响较大。目前，Kalker的三维弹性体滚动接触理论被广泛应用。本文也采用Kalker的FASTSIM 算法对轮轨接触问题进行计算分析。该方法将接触斑划分成nx×ny单元格，并假设接触斑内任意一个点(x,y)的弹性位移u与同方向面力p和柔度系数L有关[8-9], 即

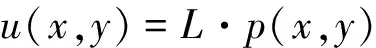
(1)

滑动方程描述如下：

(2)

式中vx,vy为纵向和横向滑动速度；vv为机车运行速度；ξx,ξy为纵向和横向蠕滑率；φ为自旋蠕滑率；u1,u2为纵向和横向弹性位移。

对式(2)进行量纲化处理得到矢量形式如式(3)所示：

(3)

式中W为总的滑动矢量;S为刚性滑动矢量; ∂p/∂x为弹性滑动矢量。

通过积分式(3)得到接触斑内任意一个单元格的切向力F(x,y)。根据库伦摩擦定理与赫兹接触理论，接触斑内单元格的切向力极限FL(x,y)如下：

(4)

式中FL(x,y) 为切向力极限值;N为法向正压力;μ为摩擦系数;a,b为椭圆接触斑的半长轴与短轴。

若F(x,y)≤FL(x,y), 则单元格处在黏着区;若F(x,y)>FL(x,y), 则滑动出现,滑动区内单元格的切向力F′(x,y)为：

(5)

把式(1)到式(5)联合起来可计算出接触区域内黏滑区分布与各单元格(x,y)的蠕滑力。因为假设接触斑内弹性变形量远小于刚性滑动量，所以计算中忽略了弹性表面变形产生的速度分量[10]。那么滑动速度的最终表达式为：

(6)

1.3 Zobory磨耗预测模型

Zobory根据接触班的能量耗散理论建立了车轮磨耗模型。在每个时间步，将接触区斑划分成黏着区与滑动区，滑动区为As，黏着区为Aa，并认为只滑动区域有磨耗, 如图3所示。对接触斑内任意一个单元格(i,j)，其磨耗能量流密度为[4]：

(7)

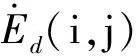
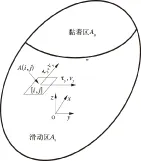
图3 接触斑内黏滑区的分布

网格单元内磨耗量流密度md表达式为：

(8)

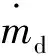
磨耗系数与能量流密度有关，式(9)给出了磨耗系数取值的条件。

(9)

上述的模型意味着在某一时刻t需要把接触斑黏滑两个区域单独考虑，这显然计算的时间较长。所以Zobory提出了简化模型：在简化模型中，认为接触班黏滑区都发生磨耗。对接触班内任意一个单元格(i,j)，其磨耗能量流密度为：

(10)

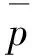
1.4 车轮踏面磨耗的平滑方法

由于预测仿真过程中机车车轮运动不是连续的过程，造成磨耗仿真预测得到的数据出现锯齿型，不符合实际情况，需要对仿真的磨耗数据进行平滑处理。对数据平滑处理问题，目前被广泛采用的方法有：快速傅里叶变换(FFT)低通滤波平滑；滑动平均法平滑；小波滤波平滑，详细过程见文献[11-13]。本文选用快速傅里叶变换(FFT)低通滤波平滑对预测的磨耗数据进行处理，并分析了该方法的平滑效果。FFT方法描述如下：

对数据{xj,j=1,2,…,N}进行傅里叶变换得到[12]

(11)

式中Xs为时间序列的频谱值；s=0,1,…,N-1。

理想低通滤波频谱函数Hs为

(12)

式中f为频率；fp为低通截止频率。

对Ys=Xs·Hs进行傅里叶逆变换即可得到滤波平滑后的数据{yj,j=1,2,…N}。

对该平滑处理方法平滑后数据和原始数据的各参数进行对比分析，见图4。结果表明两者的相关系数为0.983 2，为高度相关，均方根误差为0.004 9 mm2，平滑后最大磨耗深度为0.090 1 mm，与原始数据的最大磨耗深度较接近。平滑后的数据能较好地反映原始数据的情况，该方式的平滑效果较好。

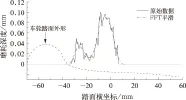
图4 原始磨耗数据与平滑处理后的磨耗数据分布

1.5 车轮踏面更新策略

机车在实际运行，车轮踏面的磨耗是连续的过程，而在仿真中不能对车轮踏面实时更新，因此只能在车轮磨耗深度或车轮运行的距离达到一定限值时再更新。由最大磨耗深度的更新策略不受线路条件的影响，而且能反映车轮踏面的状态，所以该策略被广泛应用。但不同更新磨耗深度对下一个仿真过程磨耗行为的影响也不同，因此对不同更新磨耗深度下的更新后车轮磨耗与更新前车轮磨耗行为进行对比分析，结果如图5与表3所示。

由表3可知，更新磨耗深度越大，更新后车轮与更新前车轮磨耗偏差越大。采用小于等于0.1 mm的更新磨耗深度，得到更新后车轮与更新前车轮磨耗深度相关系数都大于0.95，为高度相关，均方根误差差较小，说明轮轨几何接触关系发生变化不大。采用大于0.1 mm的更新磨耗深度，相关系数降低，均方根误差偏差较大。对仿真速度和仿真精度综合考虑，选取0.1 mm磨耗深度为踏面更新策略。

图5 更新前与更新后车轮磨耗深度分布

更新磨耗深度/mm00．010．050．100．150．20均方根误差/10-3mm200．08110．94431．19943．29025．6656相关系数1．00000．99690．97270．94810．63460．4401

2 D20E型机车车轮磨耗仿真分析

根据上述的仿真计算过程，对D20E型机车在运营一定距离后的车轮型面磨耗量分布及踏面形状进行分析，如图6,图7所示。

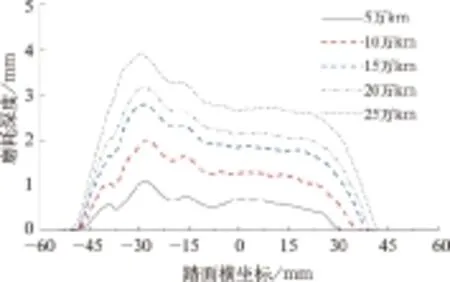
图6 车轮踏面上的磨耗深度分布

图7 车轮磨耗后踏面形状

由图6可见，车轮踏面上(-50～45 mm)区间是发生磨耗的主要范围，在轮缘根部处(-37～ -26 mm)范围内，磨耗深度最大，明显大于其余部分，与现场测量数据吻合较好。机车在运行初期车轮型面的磨耗分布较均匀；随着运行距离的增加，车轮轮缘根部处的磨耗更加明显，踏面磨耗发展规律基本相同。机车运行5×104，10×104，15×104，20×104，25×104km后，圆周磨耗深度分别为0.690，1.265，1.847，2.137，2.667 mm。

根据文献[14]，测量了D20E型机车在相同运营距离的车轮磨耗量。机车运行10×104，15×104，20×104km，踏面磨耗量均分别约为1.487，2.019，2.458 mm。仿真计算结果较实际测量结果低，原因在于：仿真的条件与实际运行条件有差别，所以磨耗系数不可能完全相同。机车在实际运行时，机车有制动，启动等过程对车轮磨耗有一定影响。模型中忽略了安装偏转角，轮径差，塑性变形等现象对车轮磨耗的影响。仿真过程中假设轨头型面保持不变，而实际上随着机车的运行轨头型面也发生变化。所以仿真的结果与实际测量数据存在一定差别是难免的。

为了得到仿真结果更加吻合实际测量结果需要进一步对模型进行修正，并将线路条件，机车状态，塑性变形等因素对车轮磨耗的影响充分考虑进去。可以通过车轮磨耗仿真模型，研究减轻机车车轮磨耗的途径和措施，对车轮型面进行优化，为机车的可靠安全运行提供一定的理论与技术支撑。

3 结束语

根据FASTSIM算法与Zobory磨耗预测模型研究了D20E型机车车轮型面磨耗的发展情况与磨耗量分布，并将仿真结果和实测结果进行了比较。研究得到以下结论：

车轮踏面上(-50～45 mm)区间是发生磨耗的主要范围，在轮缘根部处(-37～ -26 mm)范围内，磨耗深度最大，与现场测量数据吻合较好。机车在运行初期车轮型面的磨耗分布较均匀。随着运行距离不断增加，车轮轮缘根部处磨耗量更加明显，踏面磨耗发展规律基本相同。

Zobory磨耗模型能较好模拟机车车轮磨耗行为，车轮型面磨耗范围和磨耗发展情况与实际测量数据较吻合，但在相同运营距离，仿真计算得到的车轮型面磨耗深度小于实际测量结果。所以要进一步对模型进行改进，并将线路条件，机车状态，塑性变形等因素对车轮磨耗的影响充分考虑进去。

[1] Olofsson U, Andersson, Bjorklund. Simulation of mild wear in boundary lubricated spherical roller thrust bearing[J]. Wear, 2000, 241(2): 180-185.

[2] 丁军君. 基于蠕滑机理的重载货车车轮磨耗研究[D]. 成都，西南交通大学，2012：3-13.

[3] Ansari M, Hazrati I A, Esmailzadeh E. Wear rate estimation of train wheels using dynamic simulation and fied measurements[J]. Vehicle system dynamics, 2008, 46(8):739-759.

[4] Zobory I. Prediction of wheel/rail profile wear[J]. Vehicle System Dynamic, 1997, 28(2): 221-259.

[5] 丁军君, 李 芾，黄云华. 基于半赫兹接触的车轮磨耗计算[J]. 西南交通大学学报，2011, 46(2):195-201.

[6] Mai Van Tham. Nghien cuu tinh nang dong luc hoc cua dau may 3 truc tren duong cong[D]. Ha Noi, Dai hoc giao thong van tai, 2007: 17-20.

[7] KALKER J J. Three Dimensional Elastic Bodies in Rolling Contact[M]. Dordrecht: Kluwer Academic Publisher, 1990.

[8] KALKER J J. A Fast Algorithm for the Simplified Theory of Rolling Contact[J]. Vehicle System Dynamics, 1982, 11 (1): 1-13.

[9] 金学松，刘启跃. 轮轨摩擦学[M]. 北京：中国铁道出版社, 2004.

[10] JENDEL T. Prediction of Wheel Profile Wear-Comparisons with Field Measurements[J]. Wear, 2002, 253: 89-99.

[11] 杨孙楷，陈庆绸. 脉冲极谱实验数据的FFT滤波[J]. 计算机与应用化学，1991, 8(2): 81-85.

[12] 裴益轩，郭 民. 滑动平均法的基本原理及应用[J]. 火炮发射与控制学报，2001, (1): 21-23.

[13] 潘 泉，张 磊，孟晋丽，等. 小波滤波方法及应用[M]. 北京：清华大学出版社，2005.

广告目次

克鲁伯润滑剂(上海)有限公司

(封2)

苏州康开电气有限公司

(封3)

北京纵横机电技术开发公司

(封4)

深圳中电华星电子技术有限公司

(前插1)

国电南瑞科技股份有限公司

(前插2)

BP石油

(前插3)

西屋(北京)企业管理有限公司

(插前4)

深圳市盛博科技嵌入式计算机有限公司

(前插5)

北京鼎汉技术股份有限公司

(前插6)

易格斯拖链轴承仓储贸易(上海)有限公司

(前插7)

苏州西门子电器有限公司上海分公司

(前插8)

上海广成涂装技术工程有限公司

(后插1)

北京纵横机电技术开发公司(城市轨道交通牵引系统)

(后插2)

北京国际城市轨道交通建设运营及装备展览

(后插3)

洛阳隆盛科技有限责任公司

(后插4)

Research on Wheel Wear of Locomotive Based on Zobory’s Model

TAOVANCHIEN(Vietnam),LIFu,DINGJunjun，QIZhuang

(School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031 Sichuan, China)

D20Etype diesel locomotive dynamics model was built by SIMPACK software, and railway model was built based on Vietnam railway line. The Zobory profile wear model and FASTSIM algorithm was used to simulation the development and distribution of wheel profile wear of locomotive, and the simulation results were compared with the measured results. The results show that wear occurs in (-50～ 45 mm) of wheel profile, the maximum wear occurs in(-37～ -26 mm)of wheel flange root. The development of wheel profile wear has the same and the wear of wheel flange root more apparent with the increase of running mileage. The wear depth of wheel profile in simulation is less than measured depth.

vehicle engineering; locomotive; wear model; dynamics simulation; FASTSIM

1008-7842 (2015) 03-0006-05

*国家自然科学基金项目(51305359)

(1982—)男，博士研究生(

2014-11-12)

U260.11+1

A

10.3969/j.issn.1008-7842.2015.03.02