电动振动台基本参数的设计及计算
邹振兴
(苏州试验仪器有限公司,苏州 215021)
电动振动台基本参数的设计及计算
邹振兴
(苏州试验仪器有限公司,苏州 215021)
阐明了电动振动台的结构及工作原理,详细论述了电动振动台基本参数的设计及计算,系统的谐振频率、机械阻抗、在机电耦合中短路环对动圈机械阻抗的影响等,并推导了其计算公式.
工作原理;系统谐振频率;机械阻抗;短路环;计算公式
1 电动振动台的结构与工作原理
电动振动台是一种把电磁能转换成振动的机械能,且传递给紧固在动圈工作台面上的试件,使试件获得振动环境效应的一种振动设备,其基本原理是将交变电流输入到处于磁场中的线圈,使通电线圈受到电磁感应力的作用,由于电磁感应力的推动,由动圈上的工作台面把运动(或加速度)传递给试件,所以电动振动台是一种传递运动(或加速度)的振动设备.磁场的产生是激磁式的.其台体结构原理如图1所示.主要由(1)台体座、(2)通风装置、(3)下导向及空气弹簧支承、(4)磁路体、(5)动圈、(6)上导向装置、(7)防护罩、(8)过位移保护装置等部分组成.
由磁环体、中心磁极、磁缸底、磁缸盖及上下两组激磁线圈组成的磁路系统,形成磁回路,在空气隙中形成一个强大的磁场,磁感应强度为B.当交变信号电流经功率放大器后,供给线圈以可变电流I=I0sinωt.根据磁场对通电导线的作用原理,可得到电磁感力F(或称安培力),其方向用左手定则来判别,大小与工作气隙磁感应强度B,线圈有效长度L及电流强度I成正比.
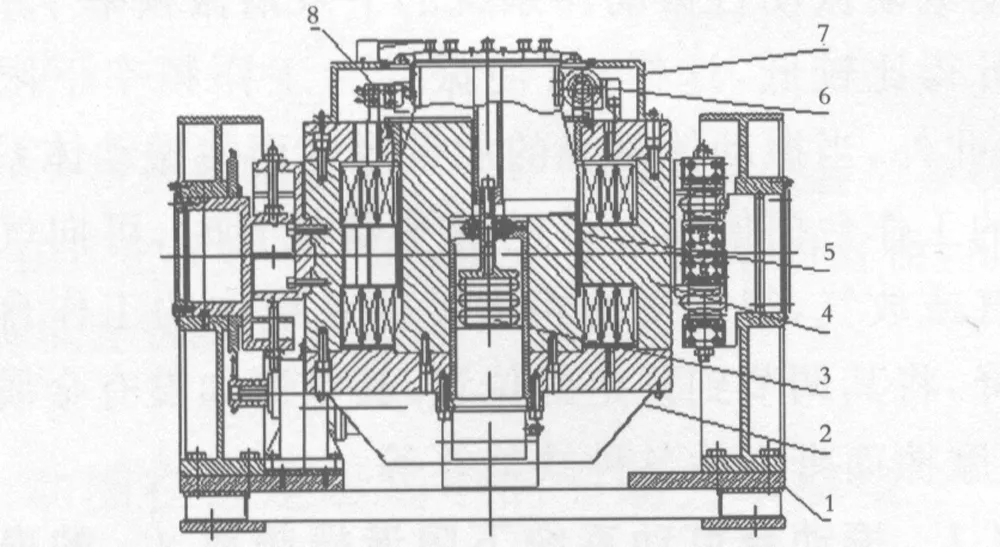
图1 电动振动台结构原理简图
电磁感应力F为:
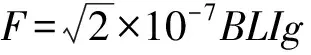
(1)
式中:B: 工作气隙磁感应强度,(GS);L: 线圈有效长度, (cm);I: 通过线圈的有效电流,(A);g:重力加速度,(9.8 m/s2).
从(1)式可以看出:电磁感应力的大小与三者均成正比,其中线圈的有效长度L和通过线圈有效电流I都是动圈确定的参数,且受到结构的限制,所以精准确定动圈线圈的有效长度和截面的大小至关重要.
2 电动振动台的动圈与空气弹簧支承系统的谐振频率
这部分的作用是把电磁能转换为产生机械振动的机械能,为试件提供要求的振动源,所以首先要求是要高效、体轻、工作频带宽、以及单位机械功能所需要的功率小等良好性能.而这些均与动圈和空气弹簧支承系统有密切的关系.
2.1 可动系统(动圈总成)谐振频率的计算
如图2所示,电动振动台动圈是由(1)线圈、(2)骨架等构件组成;而骨架则是由圆筒体、筋板、圆台等元素组成一个所谓连续系统的构件,其谐振频率的计算已有较为成熟的计算方法.而要得到实际要求的谐振频率,一般在生产中,往往是计算、制造出样机、测试交替进行,看动圈工作时的谐振频率是否高于频带上限频率.反之,则在保持动圈质量不变的条件下,适当加厚影响动圈刚度的筋板、或增加筋板数、或适当减小动圈的高度,使动圈骨架的高度H1与直径D之比为0.93左右,最后确定一个最佳的结构尺寸.可动系统(即动圈总成)的刚度是由动圈骨架的刚度K1和线圈与骨架粘贴影响而造成的弹簧刚度K2串联后而成形的刚度.
2.1.1 动圈骨架刚度K1的表达
从图2可知,可以把它看成是动圈骨架筋板的拉压刚度和弯曲刚度串联而成.这样的计算是比较简单的.
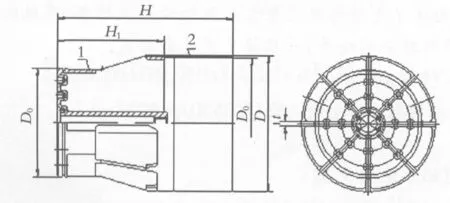
图2 动圈结构图
筋板的拉压刚度K1.1为:
(2)
筋板的弯曲刚度K1.2为:
(3)
则动圈骨架的刚度K1为:
(4)
式中:
E1:动圈骨架材料的杨氏模量,对铝合金材料其值为:7.0×105(kg/cm2);
t: 动圈骨架筋板的厚度,(cm);D: 动圈骨架的外径,(cm);
H1: 动圈骨架的高度,(cm);A:动圈骨架筋板数系数.
2.1.2 不锈钢网孔薄板和线圈与骨架粘贴影响而造成的弹簧刚度K2的表达式
线圈与骨架的联接是分别在线圈内外圆柱表面分别各粘贴一片不锈钢网孔薄板,而后一 起紧密粘贴在动圈骨架联接环下端.其机械等效系统如图3所示.由于不锈钢网孔薄板影响而造成的弹簧刚度K2的表达式为:

(5)
式中:
Dcp:不锈钢网孔薄板的平均直径,( cm);
t1:不锈钢网孔薄板厚度×2 ,(cm );
H2:不锈钢网孔薄板的高度,(cm);
E2:不锈钢网孔薄板的轴向弹性模量,
其值为:E2=2.06×106(kg/cm2).
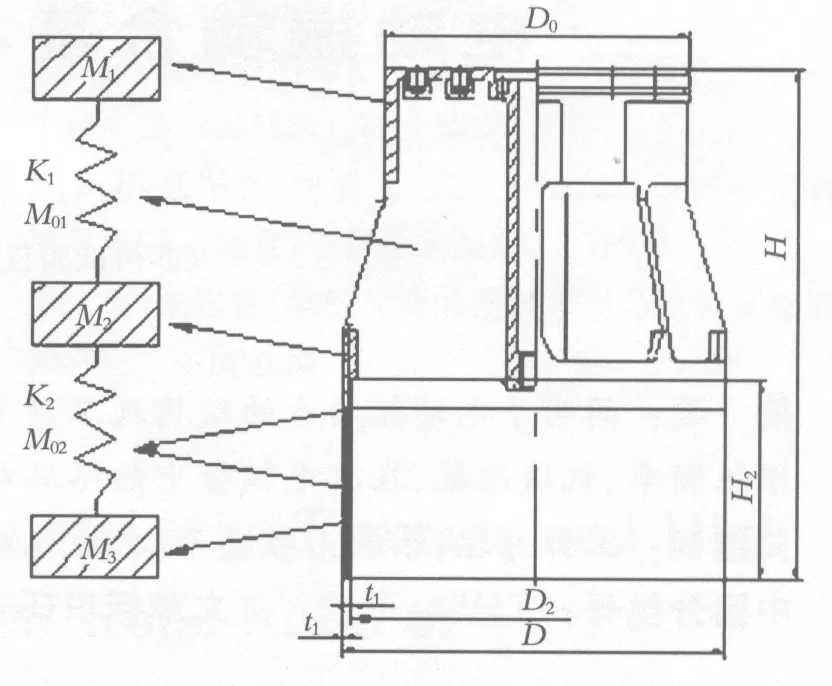
图3 动圈的机械等效系统图
2.1.3 可动系统(动圈总成)上限谐振频率fn上计算表达式

(6)

式中各符号的含义如图3和上面所述.
为保证电动振动台要求的频率特性,计算得到的可动系统上限谐振频率必须比要求的工作频率上限高出1.5倍以上.
2.2 空气弹簧支承系统的谐振频率的计算
电动振动台工作频率下限一般要求是在5 Hz.所以支承弹簧K弹值就决定了电动振动台振动体系统的最重要参数-下限谐振频率fn下,故支承弹簧为电动振动台的基本要素和重要元件之一.
在诸多种弹簧中,空气弹簧由于K弹值小,因而可使电动振动台振动体系统的下限谐振频率fn下可设计得比较低,这样,可使振动台工作频率下限较低;此外,当振动体系统的质量改变而使振动体系统中的工作台面偏离设计的静平衡位置时,可向气室充气或放气,很方便的将振动体系统中的工作台面升降,将其调节到预定的位置.其它诸如没有金属接触、摩擦而带来的各种缺陷等等.
2.2.1 振动台可动系统下限谐振频率fn下的表达式
(7)
式中:K弹:空气弹簧刚度,(kg/cm );g:重力加速度,( 981 cm/s2);W:振动台可动体系统(动圈总成)的质量,(kg).
2.2.2 空气弹簧结构尺寸及工作原理
图4为支承空气弹簧结构尺寸图,主要由四大件,即(1)气室、(2)皮囊、(3)活塞和(4)导向轮等组成.活塞与动圈骨架紧固联接.当振动台的振动体系统工作台面垂直向下运动时,与其固接的活塞就压缩密闭于气室中的空气,同时整个气簧结构对活塞产生一个向上的反力,这就是空气弹簧.

图4 空气弹簧支承结构图
2.2.3 空气弹簧刚度K弹的表达式
我们可以在机械设计手册中找到对于多曲囊式空气弹簧轴向刚度的计算式为:

(8)

P:空气弹簧的内压力,(kg/cm2);Pa:大气压力,(kg/cm2);
V:空气弹簧有效体积,(cm3);A∶承受作用力的有效面积,(cm2);
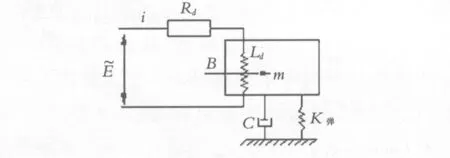
ra:空气指数,一般动态过程,其值为:1 (9) 分析弹簧刚度K弹值表达式中有关各项参数可知:在其它参数不变时,适当减少活塞的直径,可有效降低弹簧刚度K弹值. 电动振动台动圈的线圈一般采用高强度漆包导线分几层绕制而成,分别用0.3 mm不锈钢网孔薄板紧密粘贴在其内外径圆柱表面上,并用环氧树脂将其紧密粘贴固定在动圈骨架上.此外,环氧树脂还能起到加强线圈电气绝缘性能的作用;同时线圈的电阻、电感等参数还直接影响到电动振台的输入阻抗、振动体系统的上限频率等. 3.1 振动力学模型 当动圈中的线圈输入交变电流时,动圈就会在恒定磁场中作往复振动,这样就可以得到动圈在恒定磁场中的振动力学模型,如图5所示.其系统振动的微分方程为: 图5 动圈振动力学模型 (10) 式中和图中符号含义为: B:工作气隙中均匀恒定磁场的磁感应强度(GS) c:支承弹簧的阻尼系数(包括空气阻尼等)(kg·s/cm); Ld:动圈及输出变压器的电感(包括外接电感),(H); Rd:动圈及输出变压器的直流电阻(包括外接电阻)(Ω). (11) 则(10)式变为: (12) 故求得Z为: 解之,得: (13) 这样求得Z为: (14) 式中: (15) 图6 机械阻抗的等效电路图 3.2 动圈电感Ld的表达式 严格的计算动圈的电感是一个十分复杂的问题.当磁通在不饱和的情况下,通常可以忽略磁钢中的磁阻,这时动圈的电感便是一个不随输入动圈线圈电流大小而变化的常数.按电感的定义,我们就可以得到动圈的电感Ld的表达式为: 当D1≫δ时,便可近似地得到: (16) 式中: δ:磁路系统中工作隙的宽度,(cm );D1:中心磁极的外径, ( cm); hp:磁路系统中工作气隙的高度,(cm );n:动圈线圈的匝数; h:动圈线圈的高度,( cm). 3.3 动圈线圈电阻Rd的表达式 动圈线圈的电阻Rd的表达式为: (17) 式中:ρ:导线的电阻率,(对铜导线)(0.0176 Ω·mm2/m);q:导线截面积,(mm2) 短路环是用高导电率铜制成的薄壁型圆筒体;分别贴合在由中心磁极外径与磁环体内孔形成工作气隙的内外两侧.所以短路环与动圈十分接近,若不计漏磁通,那么输入动圈的电流产生的磁通φd及短路环产生的磁通φT都同时键链着动圈和短路环,如图1所示.从(13)式我们进一步可以得知,动圈阻抗在低频时,主要是电阻性的,而随着工作频率的升高会急趋升高.这样,当功率一定时,随着频率的升高,振动台的加速度会急趋下降,以致于影响工作,所以要从电气特性上延伸其工作范围,就一定要设法降低动圈的输入阻抗.而短路环正好起到了改变动圈的电阻抗的重要作用. 4.1 短路环对动圈输入阻抗的影响 当动圈输入交变电流后,带有短路环的工作气隙就构成一个类似于筒形变压器,其等效电路如图7所示. 图7 动圈与短路环耦合等效电路图 根据变压器作用原理,由基尔霍夫定理,可以得到它们的运动微分方程式为: (18) 图中和式中符号含义为: RT-短路环的直流电阻, (Ω);LT-短路环的自感, (H); MTd-动圈与短路环的互感, (H) 设E=Emejωt,i=Imejωt,iT=ITejωt,代入(18)式,则有: 解之,得到: (19) 故有短路环后,动圈阻抗Z为: (20) 将(15)式代入(20)式,并经适当整理后,可得: (21) (21)式就是在有短路环的工作气隙中动圈运动时,阻抗量值的具体计算式. 从(20)式动圈阻抗Z值还可以写成: (22) (23) (24) 由(23)式可知,当无短路环时,即η=0,把它代入(24)式,得到: Z=R0+jωL0 (25) 而当采用短路环环,并令η→1,代入(24)式,则又可得到: (26) 由此可见,在短路环与动圈线圈有足够强的感应耦合的情况下,短路环能在宽频率范围内显著地减小总阻抗.这种补偿的方法,实际上是利用了线圈的互感来抵消自感的原理,从而使动圈高频电阻抗特性大大的得到改善,降低了功率放大器的容量和动圈的温升. 采用短路环,由此而使工作气隙宽度加宽,因而会使工作气隙的磁感应强度下降,从而导致推力下降;或增加激磁线圈的容量,这样,又导至磁路体体积的增大.另外短路环使有功电阻增大,会使短路环、中心磁极和磁环体发热,故恰当地选用短路环的材料、尺寸和合适的制造质量,就甚为重要. 4.2 短路环电阻RT计算表达式 为了简化起见,假定短路环中的电流是均匀分布的.当频率不太高,而振幅又较大时,我们可以求得短路环的电阻RT为: (27) 式中:D1:短路环的内径(或中心磁极直径),(mm);DT:短路环的外径,(mm); hT:短路环的高度;(mm);ρ:短路环材料的电阻率,(Ω·mm2/m),铜为:ρ=0.0176 . 4.3 短路环电感计算表达式 严格地计算短路环的电感是一个十分复杂的问题.当磁路中的磁通在不饱和的情况下,通常可以忽略磁钢中的磁阻,这时短路环中的电感便是一个不变的常数,这时短路环的全磁通φT为: 从而得出短路环的电感LT为: (28) 式中:δ:工作气隙的宽度,(cm);hp:工作气隙的高度,(cm); hT:短路环的高度,(cm);μ0:空气磁导率系数,μ0=0.4π×10-8(H/cm ); 4.4 短路环与动圈互感MTd计算表达式 短路环与动圈之间的互感可以由短路环中的电流iT所建立的磁通键链于动圈的全磁通来求得.而键链于动圈的全磁通φTd为: 当Dcp≫δ时,则有: 从而得到短路环与动圈之间的互感MTd为: (29) 式中:h:动圈线圈的高度,(cm).n:动圈线圈的匝数.其它符号的含义及单位如前所述. 前面论述的这些参数,关系着电动振动台性能的优与劣,工作频率范围宽与窄;而动圈输入阻抗计算是否准确至关重要,电气功率放大器就是根据这一参数而设计计算确定功率放大器各个相关的参数;所以它关系着机械部分与电气部分功率放大器能否相匹配的问题,也就是说该电动振动台能否正常工作的问题. 已知某电动振动台与设计计算有关的主要性能技术参数为:①最大正弦激振力:29400 N;②额定频率范围:5~2500 Hz;③扫频范围:5~2500 Hz;④空载额定位移:(峰-峰值)51 ;⑤额定加速度:850 m/sec2;⑥额定负载:500 kg;⑦工作台面尺寸:φ320 mm ,等等.要求设计计算:①振动台振动体系统上、下限谐振频率;②动圈的输入阻抗等.这些参数的确定是需要经过多次的设定和计算,最后才能得到最佳的组合参数. 5.1 动圈基本参数的设计计算 5.1.1 设计并确定动圈的线圈导线相关参数 (1)设定工作气隙的磁感应强度B=16000 GS,工作气隙的高度hp=126 mm; 5.1.2 计算动圈骨架的刚度 按图2所示,则有:D0=320 mm,动圈的外径,D=1.25D0=1.25×320=400 mm,其中:1.25为动圈骨架下端直径(也是线圈直径)与工作台面直径之比,是经验数据.初设定动圈骨架高度为:H1=350 mm ;筋扳厚度t=12 mm .骨架的材料为ZL302铝合金,其杨氏模量为:E=7.0×105kg/cm2.则 5.1.3 计算不锈钢网孔薄板结和线圈与骨架粘贴影响而造成的弹簧刚度K2 5.1.4 计算振动台可动系统的上限谐振频率fn上 (1)计算几个相关的参数 工作台面的质量M1,M1=5.25 (kg );联接环的质量M2,M2=2.69 ( kg) 线圈的质量M3,M3=10.72 (kg );筋板的质量M01,M01=12.56 ( kg) (2) 计算振动台可动系统上限频率fn上 5.2 计算振动台可动系统下限谐振频率 5.2.1 振动台可动系统(动圈总成)的质量 振动台可动系统(动圈总成)的质量由骨架、线圈、台面螺套以及其它辅助件等质量的总和,即: W=W1+W2+W稿=20.5+11.76+1.94=34.2 5.2.2 计算空气弹簧支承的弹刚度K弹 如图3所示,设定支承空气弹簧结构尺寸的数值. (1) 计算皮囊形状系数α (2)计算气压承受平面的面积A (3) 计算空气弹簧气室容积V (4)计算支承空气弹簧的弹簧刚度K弹 5.2.3 计算振动台可动系统下限谐振频率fn下 5.3 计算动圈的阻抗Z (1)计算动圈的电感Ld与线圈导线直流电阻力Rd (2)计算短路环的电感LT与直流电阻RT (3)计算短路环与动圈互感MTd (4)按式(25)计算数个频率点的阻抗Z的数值 表1 阻抗计算值 上面设计计算的电动振动台的参数,在动圈与磁路键链以后,我们对整机的各个参数进行了测试, 检测的结果为:最大正弦激振力为29550N;最大加速度为860m/s2;振动位移幅值为(峰-峰值)51mm.并同时进行了扫频试验检测,从电频记录议画出其工作频率段5~2500Hz加速度-频率特性曲线,如图8所示. 并且与计算各个频率点的阻抗值绘制成的阻抗-频率特性曲线基本相吻合. 图8 空载加速度—频率曲线图 [1] 张维屏.机械振动学[M].冶金工业出版社,1983. [2] 谷口修.振动工程大全[日][M].尹传家译,机械工业出版社,1986. [3] 秦曾煌.电工学[M].高等教育出版社,1964. Design & Calculation of Basic Parameters of Electrodynamic Vibrators ZOU Zhen-xing (Suzhou Testing Instrument Co.,LTD , Suzhou 215021, China) This article describes the structure and the working principle of electrodynamic vibrators.and proposes the design and calculation of basic parameters of electrodynamic vibrators, the system natural frequency, the machining impedance, the short circuit ring affecting machining impedance of moving circle on coupling of machine and electron and so on. The calculation formula is given. working principle;system natural frequency;machining impedance;short circuit ring;calculating formula 2014-10-08 邹振兴(1940-) ,男,高级工程师,研究方向:电动振动及设计. TH534+.2 B 1671-119X(2015)02-0027-07
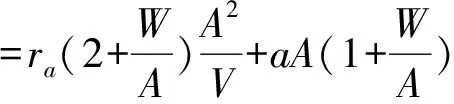
3 动圈在恒定磁场中的振动力学模型
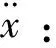



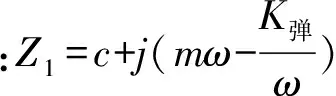


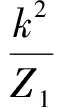


4 短路环的设计



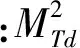

5 应用举例








