一种新的动态聚类算法在高职就业分析中的应用研究
张 强
(安徽商贸职业技术学院,宿州 241002)
一种新的动态聚类算法在高职就业分析中的应用研究
张 强
(安徽商贸职业技术学院,宿州 241002)
为解决常用于就业数据信息分析的 K-means算法中初始化聚类中心敏感和容易陷入局部最优值问题,提出了一种新的动态聚类算法.该算法首先利用最近邻聚类法获得初始聚类中心,然后利用小类对合并条件进行聚类合并,从而获得更优的聚类结果.以多个高职院校近几年的就业数据为样本信息,在数据预处理的基础上,运用提出的聚类方法进行了聚类实验分析,并挖掘出与就业质量相关的因素.最后的实验结果表明,文中提出的聚类方法聚类划分效果更优.
数据挖掘;聚类;就业数据分析
0 引 言
当前高职院校毕业生就业问题日益突出,同时就业质量的好坏也成为社会普遍关注的问题[1],如何更好的指导学生应业,从海量的就业数据信息中挖掘出与就业有关的因素和潜在的联系,是目前研究的热点之一[2].本文针对K-means算法在聚类过程中出现初始化聚类中心敏感和容易陷入局部最优值问题,提出了一种新的动态聚类算法,抽取合肥地区几所高职院校的就业数据信息为样本数据,运用提出的聚类算法进行聚类分析,首先采用最近邻聚类法生成初始聚类集[3],然后采用合并条件对满足合并要求的小类对进行合并优化[4],从而获得更优的聚类结果.
1 动态聚类算法
确定聚类的个数和相应的聚类,是聚类分析要解决的两个主要问题,而大多数研究却只关注第二个问题,就是在已给定聚类个数的情况下进行聚类.但事实上,对于很多数据,我们无法事先确定聚类的个数.为解决聚类中最优解的问题,在综合考虑聚类算法的效率及性能的基础上,本文提出了一种新的动态聚类方法,该方法分为两个阶段:
(1)近邻聚类阶段:采用最近邻聚类算法进行初步聚类,并根据相异性和相似性度量过滤掉聚类中的异常类,构建初始的聚类集.
(2)合并优化阶段:利用动态的聚类评估函数,进行聚类划分,从而获得接近最优的聚类结果.
1.1 近邻聚类
最近邻聚类算法的思想是如果两个距离最近的样本直接的距离小于设定的阈值d,就可认为它们属于同一类.该算法是在数据相似度矩阵上进行聚类的,采用欧几里德距离作为样本相似度的测试指标.样本xi和xj的相似度计算公式为:
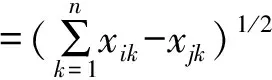
(1)
算法的具体聚类步骤如下:
(1)选取未聚类的任意一个样本作为x1第一个聚类C1的聚类中心,C1=x1,设定相似度阈值为d1.
(2)取下一个样本x2,计算x2到x1的距离d21:若d21<=d1,则x2∈C1聚类;否则将x2作为新类C2的聚类中心,C2=x2,设定相似度阈值为d2.
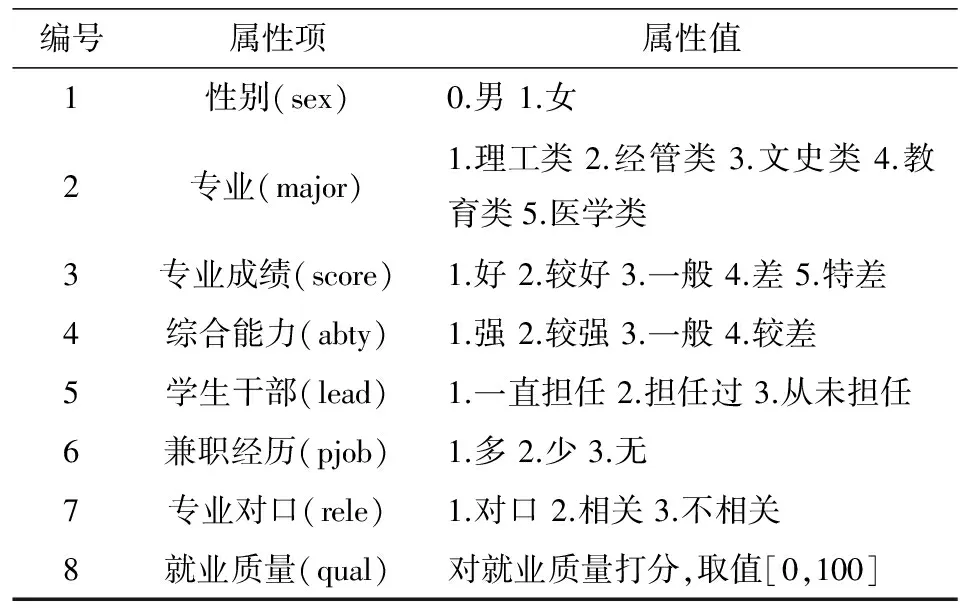
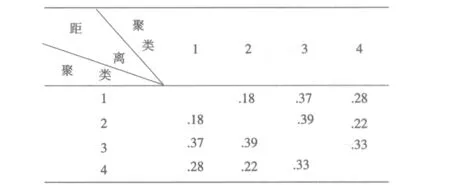
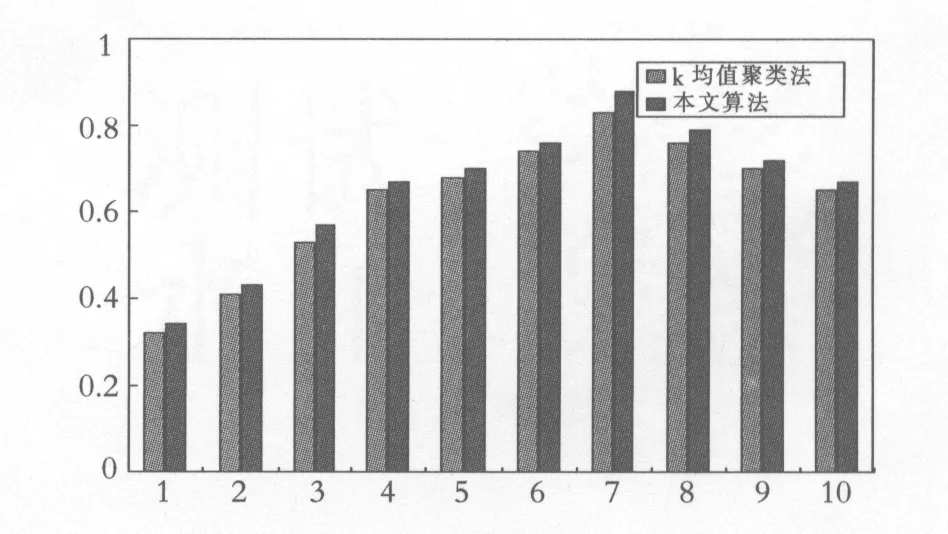
(3)设存在K个聚类C1至Ck,继续取样本xi,分别计算xi与K个聚类中心的相似度,若xi与聚类Cj的聚类中心的相似度dij (4)重复执行步骤3,直至所有的样本分类完毕,获得初始聚类集C. 1.2 聚类合并优化 由于最近邻聚类算法在聚类中会产生很多子类,需要进行适当的合并优化,才能获得满意的聚类效果.事实上,任何一个类或者延伸形状的类族可以用多个中心表示,为此我们提出了小类合并算法,该算法采用内聚力为合并条件[5].为更好的描述聚类合并的过程,首先引入几个定义: 定义1:类Ci中的一个样本xi与另一个类Cj的粘合能力为con(xi,Cj): (2) (3) 基于内聚力的小类合并算法步骤如下: (1)输入初始聚类集C=C={C1,C2,…CN}; (2)计算所有子类之间的内聚力coh(Ci,Cj)和所有类间内聚力平均值coh*,并将作为合并条件,若coh(Ci,Cj) (3)对所有小类对进行判断,根据评估函数看它们是否满足合并要求; (4)将所有满足合并要求的小类对进行筛选,并组成一个队列; (5)从队列中选择出对头,如果队列为空,则转步骤(7); (6)根据合并条件判断对头这两个小类是否可以合并,转步骤(5); (7)合并聚类结束. 将动态聚类算法运用于高职学生就业信息数据库,对相关的就业数据进行聚类分析,挖掘出一些有用的信息,使得高职院校在就业宣传,就业规划设计及专业设置等方面提供决策依据,从而实现使得毕业生能够更快更好的就业. 2.1 数据采集 本研究中,收集了合肥地区3所高校学生就业信息数据库中的近3年的毕业生就业信息,就业数据真实可靠,且数据来自于不同高校,因此具有实用性和广泛性.就业信息从大的方向来分,可分为个人基本信息、教育信息、就业信息和就业质量四个部分,而不同数据部分中的数据属性可能会出现重复或者与聚类分析无关,因此要对采集到的数据信息进行处理. 2.2 数据预处理 聚类前是否有效的对数据进行预处理将影响挖掘的效果与质量,因此在进行数据聚类挖掘之前要进行必要的数据预处理,文中的处理过程主要有以下几步: (1)数据清洗.对就业信息数据库中无效的数据记录进行删除,而对遗漏数据的处理主要是通过忽略该条数据记录、均值填补、缺省值填补等方法进行处理. (2)抽取数据属性.从四部分数据信息中抽取出与就业有关的属性,如性别、专业课成绩、外语等级、计算机等级、技能等级、课外兼职经历、是否党员、就业单位、工资情况等属性.由于属性间存在联系或者将多个属性相结合也能反映就业情况,如可以讲工作环境、工资满意度及有无发展前景等属性合并,生成就业质量属性. (3)数据转换.由于属性数据取值范围不固定,因此要对属性进行离散化处理,并采用加权法进行归一化处理.如专业课成绩是由各个学期所学的不同专业课程成绩组成,数据量较大,因此要进行综合处理,把各专业成绩进行加权汇总或求平均和,然后根据加权值把专业课成绩分为四级:优、良、较好、差. 考虑到数据运算过程的运算量,文中仅选择了与就业相关的8个属性,如表1所示. 表1 就业数据属性项 2.3 数据聚类分析 为了检测本文提出的动态聚类算法的有效性,从就业数据信息库中随机抽取出15条记录,并进行了归一化处理,作为聚类用的测试样本数据,如表2所示. 表2 处理后的就业样本数据 采用本文提出的动态聚类算法,进行第一阶段的最近邻聚类分析,获得6个聚类结果作为初始聚类集C: C={{1,4,7},{8,12},{3,5,6,9,13},{15},{2,10},{11,14}} 在第二阶段,采用内聚力为合并条件将小类对进行合并,获得4个聚类结果作为最终的聚类集: C={{1,4,7,8,12},{3,5,6,9,13},{15},{2,10,11,14}} 根据欧式距离公式,计算各聚类间的距离如表3所示. 表3 各聚类间的距离 由表3可知4个聚类间的距离很大,而各个聚类内部样本数据间的距离很小,实现了样本数据在不同聚类间的差异和同一聚类之间的相似. 从第一类{1,4,7,8,12}聚类结果可以看出,该组样本数据的就业质量偏低,其特点是样本数据都是女生,专业成绩一般,很少是学生干部且就业和所学专业几乎不相关. 从第二类{3,5,6,9,13}聚类结果可以看出,该组样本数据就业质量较好,其特点是样本数据大部分是女生,学生干部居多且都有兼职经历,而综合能力一般,就业和所学专有一定相关性. 而第三类{15}聚类结果从表3可以看出,该类与其他几个类的距离都很大且只有一个样本数据,因此可将该类判定为异类. 从第四类{2,10,11,14}聚类结果可以看出,该组样本数据的就业质量是最高的一类,其特点是样本数据都是男生,综合能力强,大部分都担任过学生干部且有兼职经历,就业和所学专业几乎对口或具有相关性. 2.4 聚类效果分析 为验证本文提出的动态聚类算法的聚类效果,采用相同的数据集,将文中提出的聚类算法和经典的k均值算法在聚类精度方面进行了对比,结果如图1所示. 图1 聚类精度比较 从图1可以看出,本文算法在聚类准确度上优于K均值聚类法,且在数据量较大时聚类个数为7个的时候,准确度最高. 以高职院校毕业生数据信息为研究对象,提出了一种动态的聚类算法,对相关的就业数据进行聚类分析.研究目的是,通过挖掘出的一些有用信息,为高职院校在教育改革及就业工作提供依据和参考,从而实现毕业生能够更快更好的就业. [1] 贾瑞玉.数据挖掘技术在高职就业分析中的应用研究[D].安徽大学,2010:8-13. [2] 杨断利,张 锐,王文显.基于模糊决策树的高校就业数据挖掘研究[J]. 河北农业大学学报,2012,35(2): 111-114. [3] 基于FCM的类合并聚类算法研究[D].重庆大学硕士论文,2009:30-35. [4] 林有城,等.基于多类合并的Pso_means聚类算法[J].计算机系统应用,2014,18(2):160-166. [5] 孙 昱,鲁汉榕. 一种基于内聚力的自合并聚类算法[J].空军雷达学院学报,2004,18(4),57-59. A New Dynamic Clustering Algorithm for Analyzing Employment Data of Vocational College ZHANG Qiang (Anhui Business College,Suzhou 241002, China) K-means algorithm for analyzing the employment data of vocational college is unable to solve the problems of the sensitivity of initialization and premature convergence. This paper proposes a new dynamic clustering algorithm. Firstly,the algorithm selects the initial cluster center by the nearest neighbor algorithm, and then carries out cluster merging based on merging condition to obtain the best clustering results. Taking the recent graduates of higher vocational colleges of education information and employment information data as the research object, on the basis of data pretreatment,and using the proposed dynamic clustering algorithm for the analysis of the sample data,the factors related to the quality of employment are found. The experimental results show that the algorithm present in this paper has a better cluster category effect. data mining: clustering: employment data analysis 2014-11-06 安徽高校省级自然科学研究项目(kj2013z090). 张 强(1982- ),男,硕士,讲师,研究方向:计算机应用技术. TP391 A 1671-119X(2015)02-0047-04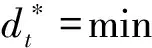
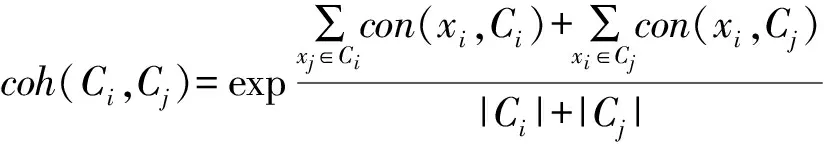

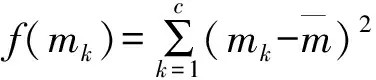
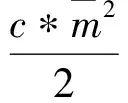

2 动态聚类在高职就业分析中的应用

3 小 结

