基于二阶阻容模型的锂离子动力电池工作特性的建模及仿真分析

杨三英

(湖南工程学院 机械工程学院，湘潭 411101)



基于二阶阻容模型的锂离子动力电池工作特性的建模及仿真分析

杨三英

(湖南工程学院 机械工程学院，湘潭 411101)

分析比较了几种常见的电池电化学模型和等效电路模型，建立了以电池电动势、电池内阻、电池容量为决策变量的二阶电阻电容等效电路模型,推导出了其状态空间模型.在matlab/simulink平台上搭建模型各个模块，最后对电池电流、电压及SOC进行了仿真分析，结果表明该模型方案设计合理可行.

动力电池；动力特性；二阶阻容模型；剩余电量

随着世界经济的高速前进，汽车工业发展迅速，对能源需求不断提高，同时给环境造成的污染日益严重，节能减排的汽车开发和制造成为全球汽车产业的主流趋势.混合动力汽车以其低污染物排放、低噪声以及多样化能源等诸多优势成为未来汽车最具开发利用价值的交通工具，是未来汽车发展的主要方向[1-3].混合动力汽车的发展仍存在瓶颈，核心表现在动力电池的使用寿命、电池的能量效率和运行的可靠性等方面.对动力电池工作状态的监测是混合动力汽车能量管理系统的重要内容，要求在高精度的电池数学模型中，结合动力电池电压、电流、温度等基本参数来准确反应电池的工作特性，因此，建立一个精确的动力电池数学模型成为电池工作状态监测的热点与难点之一.

1 锂离子动力电池

电动汽车具有节能、环保的巨大优势，但对动力电池的基本要求较高，表现在高比容量、比功率、高连续放电率，低自放电率、循环寿命长、电池性能衰减慢、使用温度范围广[4-8]等诸多方面，常用的动力电池有高功率铅酸蓄电池、镍氢蓄电池、锂离子蓄电池，表1给出了三种动力电池性能优缺点、表2给出了36 V 10 Ah动力电池性能对比情况.从表1、表2可以看出，锂离子蓄电池是一种新型的高能电池，具有比能量高、体积小、质量轻、循环性能好、使用温度范围宽和寿命长等优点，具有较大的开发潜能和研究价值[9].

表1 动力电池性能比较

表2 36 V 10 Ah动力电池性能对比

锂离子动力电池主要由正负电极、隔膜、电解质三部分组成，一般正极采用锂化合物LiXCoO2, LiXNiO2或LiMn2O4，负极主要材料为石墨，电解质溶液则要求具有较好的传输锂离子的性能.

以LiCoO2/C的锂离子电池为例，其正负极及总反应为：

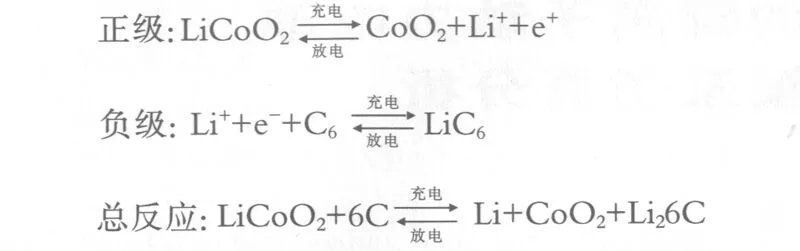
在充电时，锂离子正极脱嵌并经过电解质嵌入负极，负极处于富含锂离子状态，放电时刚好相反，锂离子的往复移动形成电流，锂离子通过电解质溶液、隔膜、在电池正负极间不断的嵌入、脱出，并不破坏电极的层状结构，是一个可逆反应的过程[10]，图1给出了锂离子工作原理示意图.

图1 锂离子电池工作原理

2 常用的电池模型分析

(1)Peukert模型

如式(1)所示，该模型认为随着放电电流的增加，电池的可用容量减小，反应了动力电池工作特性的重要方面，是较为经典的电池模型，但该模型只考虑了放电电流以及放电时间的关系，忽略了温度、电压、电池老化等因素对电池电量的影响.

ik·Ti=C

(1)

其中，i为工作电流，Ti为工作电流为i的充放电时间，k为电池常数，C为常数.

(2)Shepherd模型

该模型考虑了电池工作电压、电池内阻、工作电流等主要因素，采用一定的模型修正系数建立上述因素与动力电池剩余电量SOC(State of Charge)的函数关系，如式(2)所示.

(2)

其中，U为工作电压，i为工作电流，R为电池内阻，k1、k2为模型修正系数，SOC为电池剩余电量.由于动力电池SOC存在较明显的非线性关系，使得Shepherd模型在小电流工作时具有较好精度，但当电流i幅值变化范围较大时，该模型产生较大的误差.

(3)Unnewehr模型

考虑到动力电池SOC较明显的非线性关系，将Shepherd模型进行改进得到Unnewehr模型，如式(3)所示,该模型在一定程度上扩大了动力电池工作电流的幅值范围.

U=k1-R·i-k2·SOC

(3)

式中，U为工作电压，i为工作电流，R为电池内阻，k1、k2为模型修正系数，SOC为电池剩余电量.

上述三种模型均考虑了动力电池的主要本体因素，可归类为电化学模型，具有一精度，但忽略了其他的使用因素对模型精度的影响，在混合动力汽车上的应用具有一定的局限性.

根据电池的外特性，电池在工作过程中会表现出电阻、电容等特性，可考虑利用基本电路元件构成电路网络来表示电池相似的特性，同时要求电路元件的基本组合要符合电池响应特点、根据模型的状态方程准确建模、有准确的测量方程以及控制模型运行的复杂度以提高其可行性.目前，常用动力电池等效电路模型有Rint模型、GNL模型、Thevenin模型.

(4)Rint模型

如图2所示，该模型采用R描述电池等效电阻，随端电压和电流的变化而变化，并没有考虑其他影响条件；Voc来描述电池的开路电压.

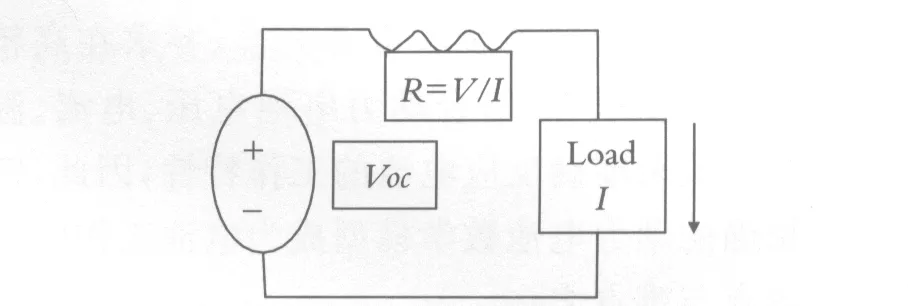
图2 内阻模型

Rint模型优点在于等效电路结构简单、参数易确定，缺点表现在考虑的影响因素少，是电池的理想状态不能模拟电池实际工作时的动态特性，在混合动力汽车复杂工况下不能使用.

(5)GNL模型

该模型的等效电路如图3所示，模型以电池的开路电压为核心，用存储能量的大电容来描述电池工作时的开路电压的变化；考虑了电池本身内阻以及电池自放电电阻；采用电化学极化电容和电阻并联于网络来描述电池的电化学极化现象；采用浓差极化电容和电阻并联于网络来描述电池内部的浓差极化现象.由于模型很好的描述了动力电池存在的各种电化学现象，反应电池工作特性比较全面，但在模型的建立复杂，状态方程确立复杂.

图3 GNL模型

(6)Thevenin模型

Thevenin模型的等效电路如图4所示，与GNL模型相似，以电池的开路电压为核心,电池的极化内阻来描述电池非电损失所消耗的电能；电池的极化电容来描述电化学反应中的扩散现象；用电池内阻描述电损失消耗的能量.

Thevenin模型结合了内阻模型的优势，同时也考虑了电池的动态特性、电池在电解过程中所产生的电容和电阻等因素，较全面的反应电池的响应特性.模型结构较GNL模型简单，在动力电池的基础建模中应用广泛.

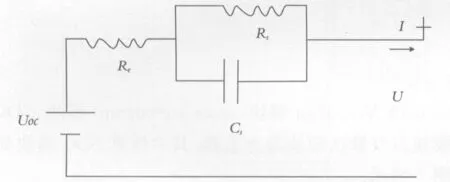
图4 Thevenin模型

3 电池工作性能模型的建立

锂离子动力电池有三个基本特性:内阻特性、电压特性和容量特性.根据上述电池模型分析，本文综合GNL模型以及Thevenin模型两者的优势，根据模型三点要求：(1)较全面的描述电池的静态、动态特性；(2)模型复杂度低，状态方程容易建立，易于计算；(3)工程实现可行.如图5所示搭建二阶电阻电容模型并在matlab/simulink平台上进行模块仿真.

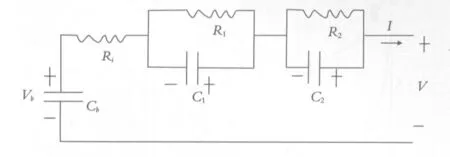
图5 二阶电阻电容模型

(4)

(5)

将式(4)、(5)进行离散化，则模型的离散化方程如式(6)、(7)所示.

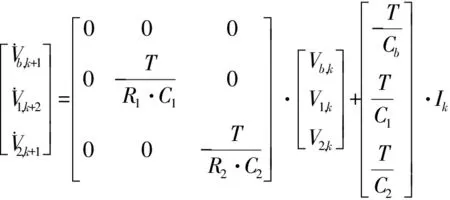
(6)

(7)

式中，T为采样时间，模型变量为Vb、V1、V2,，锂离子电池的工作电流为系统输入信号，设为u，其工作电压为系统输出信号，设为y，可设：x=[x1x2x3]T=[VbV1V2]T

则式3.3、3.4可表示为：

(8)

其中：

式(8)即为该二阶电阻电容模型中锂离子电池离散状态空间模型.

4 电池工作性能模块的建立

本仿真中采用6 Ah saft锂离子动力电池，考虑温度、老化及电池输出功率对电池剩余电量SOC的影响，在matlab/simulink平台上进行仿真，深入研究锂离子动力电池的特性.电池整体仿真模块如图6所示.

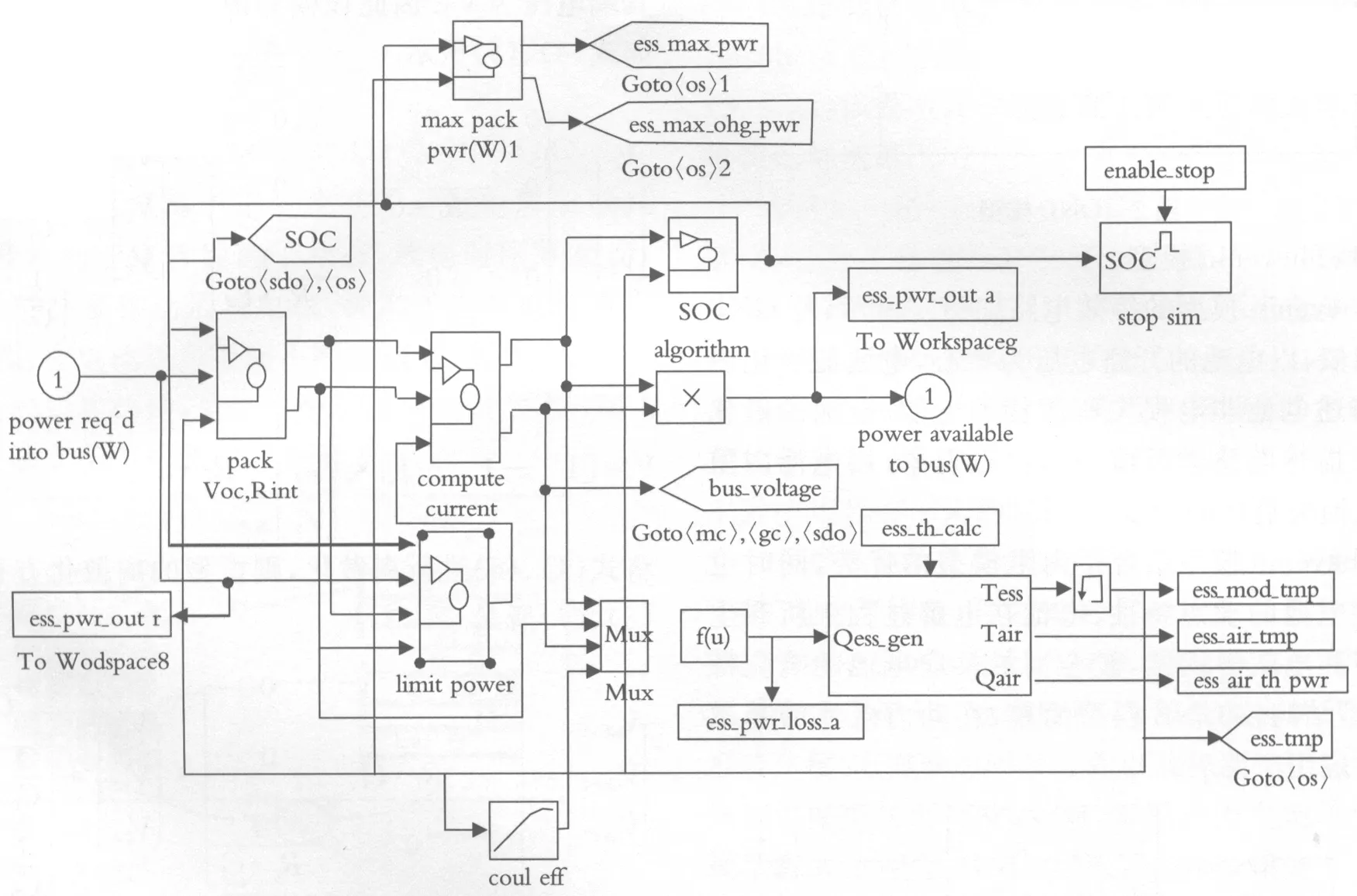
图6 锂离子电池模块

电池整体模型主要包含电池开路电压和内阻计算模块(pack Voc.Rint模块)、功率限制模块(limit power模块)、电池负载电流计算模块(compute current模块)、SOC模块以及散热模块五大模块，其中以pack Voc.Rint模块、compute current模块、SOC模块以及算法模块最为重要，其中估算SOC模块如图7所示.

图7 SOC模块

5 模型仿真结果及分析

(1)电池Capacity特性

随着放电电阻、放电温度的变化，电池安时量(Capacity)呈指数减小；同时，放电温度越高，电池安时量越大.在三种放电电阻、放电温度的情况下电流与电池容量的关系曲线如图8所示.在静态估计电池容量时，可采用电池的开路电压OCV值来计量；用开路电压误差百分比的绝对值来衡量模型在试验中的准确度，本仿真模型的电池OCV估算值(25.9 ℃试验工况)平均误差控制在3%左右.

图8 电池容量特性曲线

(2)电池充放电Rint特性

在充放电初期，电池内阻基本稳定；随着充放电温度的变化，其内阻发生了改变.如图9所示，放电初期内阻值在0.005 ohms附近，到中期电池内阻开始波动频繁并呈现上升趋势；在放电过程快结束时，电池内阻呈指数增大，放电效率急剧下降，放电终止；充电过程则相反，如图10所示.

图9 电池放电时内阻特性曲线

图10 充电时内阻特性曲线

(3) 综合仿真

基于上述电池单一特性，电池的单体电压、电流及容量仿真结果如图11、图12所示，表明单体电池最高电压可以达到3.9 V，最大容量为6 Ah，平均误差在1.02%，较好的反映了电池实际特性；最后，如表3所示，给出了实验中部分充电时极小值电压与电池SOC的变化值以及放电时极大值电压与电池SOC的变化值，数据验证了模型的精度.

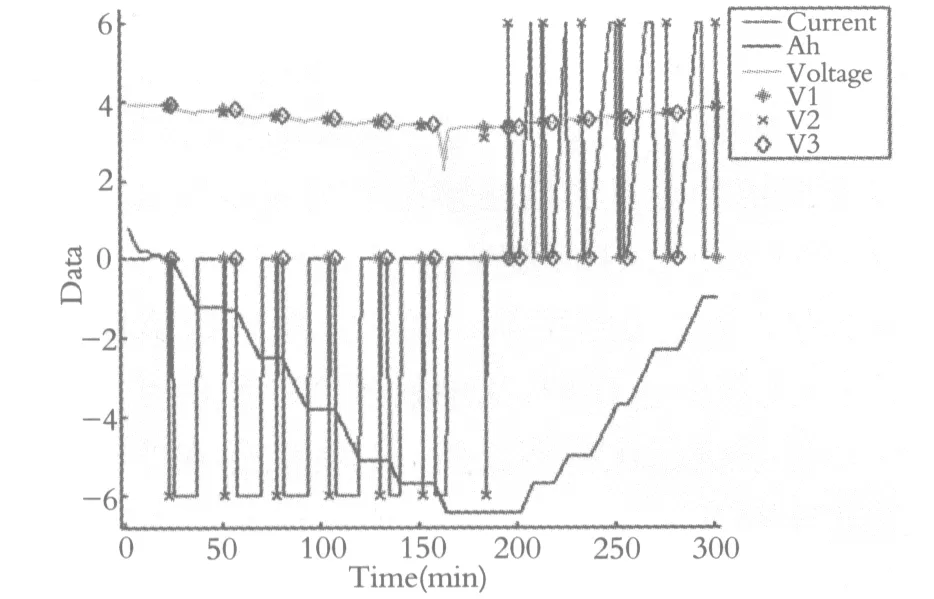
图11 单体电池电压/电流/容量综合曲线

图12 单体电池电压及电压误差分布

充电放电电压极小值(V)SOC电压极大值(V)SOC3．30110．17893．21240．15323．45210．25423．34100．21343．59880．37753．54790．25863．64100．52823．69410．48263．77630．62313．75300．58223．80640．79893．79410．68453．89330．85263．84210．74143．94120．93513．90010．8994

6 结 论

本文探讨了锂离子动力电池工作原理以及常用的锂离子电池电化学模型和等效电路模型，建立了二阶电阻电容等效电路模型并进行了模块的搭建和仿真分析.仿真结果发现锂离子动力电池容量受温度影响较大；工作过程中电池内阻变化主要受充放电的电流大小影响；同时，在动力电池电流、电压及功率仿真方面该模型具有较好的精度，为电动汽车动力SOC的估算提供模型参考与扩展.

[1] 陈清泉.电动汽车的现状和发展趋势[J].科技导报，2005 23(4):24-28．

[2] 杨孝纶.EV技术发展趋势及前景[R]．2007年汽车工程学会年会专题演讲,2007．9．

[3] 孙立清.汽车节能与环保技术[J]. 新材料产业，2006,(12)：40-44．

[4] 唐德修.对燃料电池推动汽车技术进步的探讨[J]．重庆工学院学报, 2006,(11)：29-31．

[5] 陈全世.先进EV技术[M]. 北京：化学工业出版社，2007．

[6] 闵海涛,程 猛.新能源汽车环境影响及能源效率分析[J].拖拉机与运输车,2007,34(4)．

[7] 廖晓军,何莉萍，钟忠华，周红丽，高学峰．电池管理系统国内外现状及其未来发展趋势[J]．汽车工程,2006，28(101)：961．964.

[8] 周 东.新能源汽车在我国发展可行性分析[J].中国环保产业，2006(1):29-33．

[9] Feilat，E．A．；Jaroshi，A．M．；Radaideh，S．M．；Adaptive Neuro-Fuzzy Techniquefor Tuning Power System Stabilizer[J]．UPEC'06．Volume 1，6-8 Sept．2006 Page(s)：170-174．

[10]M．Urbain, S．Ra?l, B．Davat, P．Desprez .State Estimation of a Lithium-Ion Battery Through Kalman Filter Power Electronics Specialists Conference[J].IEEE,2007,17(21): 2804-2810．

Simulation and Analysis of Model and Performance Characteristics for Iithium Power Battery Based on RC Model

YANG San-ying

(College of Mechanical Engineering, Hunan Institute of Engineering, Xiangtan 411101, China )

This article discusses the model of the li-ion battery, The electrochemical models and equivalent circuit models.The second-order RC network equivalent circuit model with battery electromotive,battery internal resistance and battery capacity as the decision variables for lithium ion battery on electric vehicle is established and the state-space model is deduced.The battery current, voltage and power of the model based on matlab/simulink are simulted and analyzed.the results prove that the model is reasonable and feasible.

power battery;dynamic characteristics;RC model；state of charge

2014-11-20

2014年度湖南工程学院校级青年科研资助项目(201404).

杨三英(1985-)，女，硕士，助教，研究方向：电动汽车控制策略、动力电池控制方法.

TM910

A

1671-119X(2015)02-0015-05