基于MIC 的CLCG4 并行化设计与实现

李智杰，周津羽，华 诚，刘 逍，，周晓辉，

(1.西安邮电大学 计算机学院，陕西 西安 710061;2.陕西省高性能计算研究中心，陕西 西安 710061)

能够产生随机数序列的软件或硬件或者二者的结合被称为随机数发生器(Random Number Generator，RNG)［1－2］。随着计算机技术的发展，随机数发生器在各个领域得到了越来越广泛应用。LCG 是目前主流随机数发生器中的一种，其优点是随机性好、产生速度快等，但周期较短。因此，如何提高随机数发生器的品质及其发生速度成为研究热点，人们提出了组合随机数发生器的思想［3－4］。L'Ecuyer 和Andres 于1997 年提出的CLCG4 是其中一种［5］，通过将4 个LCG 发生器组合能够克服LCG 发生器周期较短的缺点。然而由于CLCG4 算法复杂度的增加，使其产生随机数的速率较慢。

现今计算机的发展可分为两个阶段:串行计算时代和并行计算时代［6］。随着基于多核处理器结构的计算机成为市场的主流，并行计算将会是计算机科学未来发展的一个方向重要，其在提高计算机硬件资源利用率的同时，可显著改善算法的性能、程序的执行速度等。近年来，并行化技术已开始应用于随机数发生器领域［7－8］，Bradley T，du Toit J 和Giles M 等人在2010年将随机数发生器的并行化方法归纳为Simple Skip Ahead，Strided Skip Ahead 和Hybrid 3 种［9］。但针对每一类随机数发生器具体的使用方法、并行化实施方案、并行化效果并没有进行阐述和说明。

本文就CLCG4 运行速度缓慢的问题，在前人工作的基础上利用Simple Skip Ahead 方法实现了CLCG4的并行化，并基于MIC 进行了性能测试分析，主要思想是通过在一个周期内划分线程和分配任务，每个线程独立的产生一段周期内的随机数的子序列达到并行化。本文研究的主要内容包括对于CLCG4 串行算法的研究和并行算法的设计;CPU 平台下并行程序的开发及性能测试;MIC 平台上的移植及性能测试;通过目前最为完备的随机数发生器测试库TestU01 进行随机数性能测试，以此来保证并检验并行化过程的正确性;最终实验数据表明，相比串行CLCG4 随机数发生器，并行后的CLCG4 随机数发生器速度有了明显提升。

1 CLCG4 串行算法及并行化方法

1.1 CLCG4 串行算法

CLCG4 随机数发生器由4 个相互独立的LCG 随机数发生器组合而成，通过将4 个LCG 发生器的结果进行合并便可得到最终的CLCG4 随机数。CLCG4 随机数发生器的递推公式如下

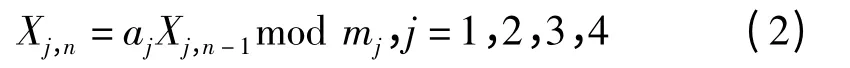
参数为a1=45 991;m1=2 147 493 647;a2=207 707;m2=2 147 483 543;a3=138 556;m3=2 147 483 423;a3=49 689;m4=2 147 483 323。

CLCG4 随机数发生器的周期可达到，通过给定初始化种子X1，0，X2，0，X3，0，X4，0就可利用以上递推公式不断生成随机数，其串行算法的程序流程图如图1 所示。

图1 CLCG4 串行算法流程图

由图1 可以看出，当产生大量随机数时，由于初始化时间很短故可忽略不计，假设随机数发生器运行一次的时间为单位1，则理论上产生random_num 个随机数所需时间约为O(random_num)。

1.2 CLCG4 并行化实现

CLCG4 并行化原理:假设CLCG4 周期为ρ，则将长度为ρ 的原始随机数序列等间隔划分为N 段，其中N 为最大可支持的线程数。每个线程从各段的起点开始递推生成随机数，并且每个线程可产生的随机数最多为个。

当需要产生random_num 个随机数并且可分配的线程数为thread_num 时(thread_num ＜N)，首先，通过4 个初始种子计算出各段的初始值，然后各线程将各段初始值作为种子开始依次计算random_num/thread_num 个随机数并输出，直至产生够random_num 个随机数为止。其并行化原理如图2 所示。

图2 CLCG4 并行化原理图

在各线程开始产生随机数之前，需根据4 个初始种子先计算出每个段的初始值，即各线程的初始种子，由式(2)可推导出

若将所有线程从0 开始编号;并且0 号线程初始值即为4 个初始种子，由式(3)可知1 号线程的初始值)计算方法如下

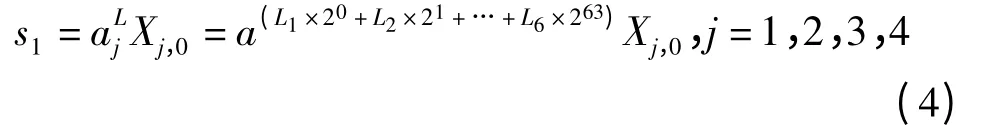
其中，L1，L2，…，L64为对应于L 的二进制中的每一位，取0 或1。由式(4)推导得

由于CLCG4 的周期约为2121，本文取L=246，即每个线程最多可产生246个随机数，且该算法最多可支持275个线程。其并行算法的程序流程如图3 所示。

图3 CLCG4 并行算法流程图

由图3 可得出，当产生大量随机数时，由于计算各个线程初始值和分配各线程任务时间较短故可忽略不计，假设各随机数发生器运行一次的时间为单位1，则理论上当采用thread_num 个线程产生random_num 个随机数的时间约为O(random_num/thread_num)，即相对于串行算法，其加速比应为thread_num，但由于线程分配及共享变量的访问等其他因素会导致加速比下降。

1.3 基于MIC 的并行化CLCG4 实现

Intel MIC(Many Integrated Core，集成众核)架构是英特尔公司专为高性能计算设计的、基于英特尔至强处理器和英特尔集众核的下一代平台［10］。MIC 在单一芯片上集成了约60 个核，每个芯片计算峰值可达到每秒1 万亿次以上的双精度浮点运算，处理复杂的并行应用是MIC 众核架构的优势。

MIC 的应用模式包括CPU 原生模式、CPU 为主MIC 为辅模式、CPU 与MIC 对等模式、MIC 为主CPU为辅模式和MIC 原生模式5 种。本文采用MIC 原生模式进行并行化，基于MIC 的CLCG4 并行化实现分为3 个步骤:(1)使用OpenMP［11－12］将串行程序并行化，通过TestU01 测试保证并行化实现过程的正确性。(2)在CPU 上进行测试性能。(3)移植到MIC 上做编译选项优化并进行性能测试。

2 实验数据及性能分析

2.1 TestU01 测试分析

目前常用的随机数发生器测试库有George Marsaglia的Diehard Tests［13］，Donald Knuth 的Classical Tests，美国国家科技标准局的NIST 以及Pierre L'Ecuyer 的TestU01［14］。因TestU01 包含共计216 种455 项测试，且分为SmallCrush、Crush 和BigCrush 3 种测试方法，其测试范围广泛而且全面，因此本文采用TestU01 作为随机数发生器测试库。

实验利用TestU01 随机数发生器测试库分别对CLCG4 随机数发生器的串行程序和4 线程并行程序进行了SmallCrush、Crush 和BigCrush 测试。图4 所示即为两者的P－value 统计分布情况，其中横轴表示P－value 的区间，纵轴表示测试结果处于不同区间的比例情况，两者均完全通过了TestU01 中455 项测试，本文将串行和并行的P－value 进行了双样本KS 统计测试，结果为0.454 4，说明两者服从同一分布。该结果在一定程度上反应了CLCG4 随机数发生器良好的随机性，且证明了并行后随机数发生器的正确性。

2.2 CPU 平台下测试分析

本实验所选用的CPU 平台为两个8 核处理器Intel Xeon E5－2680@2.7 GHz，最多支持16 个线程，在测试中分别对1、2、4、8 和16 个线程下产生1 000 000、10 000 000、100 000 000、1 000 000 000 及10 000 000 000个随机数的运行时间进行了测试，测试结果如表1所示。

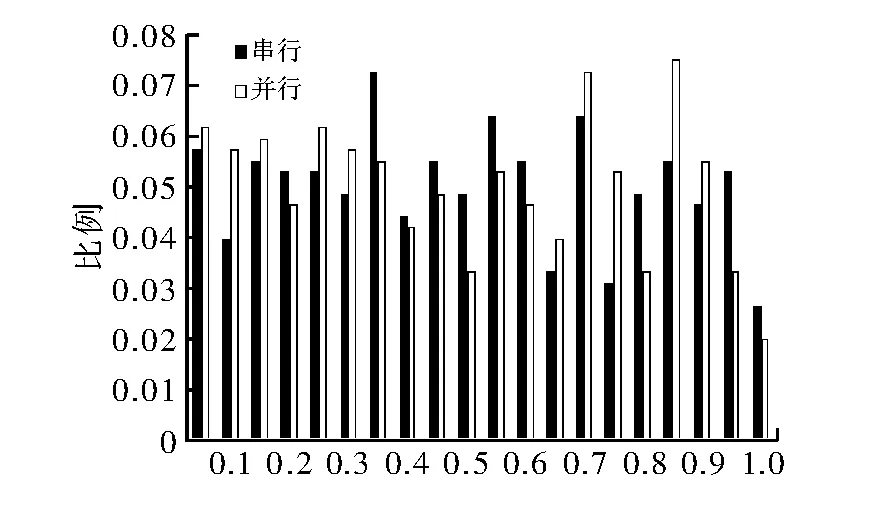
图4 串行与4 线程并行程序TestU01 测试P－value 统计

表1 基于CPU 的时间测试

通过对表1 时间测试的结果进行分析，其加速比情况如图5 所示。

图5 CPU 平台下的加速比

测试结果表明，当所需产生的随机数较少时，加速比并不明显，这是因为当生成的随机数较少时，总的运行时间太短以致于初始化程序时间占较大比例，而各个线程并行产生随机数的时间占用比例较小。因此随着线程数的增加其加速比甚至有下降的情况;当产生随机数较多时，加速比并无随线程数的增加而线性增长，这是因线程数增加时，各线程和内存之间交换的数据量增大，创建和销毁线程将占用一部分系统资源及计算机系统对线程的调度管理都将降低并行效率。从图中还可看出，当线程数相同时，随着产生随机数数量的增加，并行效率也随之提高。

2.3 MIC 平台下的测试及分析

本文所用的MIC 平台为Intel Xeon Phi 3110P 57cores@1.10 GHz，首先在224 个线程下产生1 000 000 000 个随机数，然后对各项编译选项进行时间测试，其中只有添加－O3 编译选项后优化效果比较明显，其相对－O2编译选项的加速比为1.46，因此本文采用－O3 编译选项。

本实验分别对1、2、4、8、16、32、56、112、168 和224个线程下产生1 000 000、10 000 000、100 000 000、1 000 000 000及10 000 000 000 个随机数的时间进行了测试，测试结果如表2 所示。

表2 基于MIC 的时间测试

通过对表2 时间测试的结果进行分析，可获得其加速比情况如图6 所示。

图6 MIC 平台下的加速比

由图6 可知，基于MIC 的CLCG4 并行化加速比效果较明显，最优加速比达117.75 倍。当产生随机数较少时，各个线程并行产生随机数的时间占总时间的比例较小，因此随着线程数的增加并行效果并不明显。当产生随机数越来越多时，性能提升效果也越来越明显，但加速比并未随线程数的增加而线性增长，这是因为线程数增加时，各线程和内存之间交换的数据量也随之增大。此外，在MIC 卡上设置的线程数并不是越多越好，线程数越多则将导致开销越大。因此要根据所需产生随机数个数设置合适的线程数以确保获得最佳的加速比。例如图6 中基于MIC 产生100 000 000个随机数时，在112 个线程左右的加速比最高，多于112 线程时加速比出现下滑趋势。此外，当线程数相同时，随着产生随机数数量的增加，加速比逐渐呈增长状态，因此该并行算法在MIC 平台上也是可扩展的。

3 结束语

本文在分析了CLCG4 随机数发生器串行算法的基础上，设计并实现了在MIC 平台上的CLCG4 随机数发生器的并行化方案，并通过TestU01 测试验证了其正确性，基于CPU 平台的性能测试和基于MIC 平台的性能测试结果表明，该方法可以有效减少CLCG4 的运行时间，提高其产生随机数的效率，使得CLCG4 随机数发生器能够更为广泛的应用于高性能领域。

［1］ Knuth D E.The art of computer programming［M］.USA:Addis on Wesley Publishing Company，2002.

［2］ Knuth D E.计算机程序设计艺术:半数值算法［M］.2 版.北京:国防工业出版社，2002.

［3］ L'Ecuyer P.Combined multiple recursive random number generators［J］.Operations Research，1996，44(5):816－82.

［4］ Tang H C.Combined random number generator via the generalized Chinese remainder theorem［J］.Journal of Computational and Applied Mathematics，2002，1422(15):377－388.

［5］ L'Ecuyer P H，Andres T.A random number generator based on the combination of four LCGs［J］.Mathematics and Computers in Simulation，1997，44(1):99－107.

［6］ 杨尚琴.多层次并行算法与MPI－2 新特性的研究及应用［D］.成都:成都理工大学，2009.

［7］ 魏公毅，杨自强.关于并行随机数发生器的若干算法［J］.数值计算与计算机应用，2001(4):311－320.

［8］ Michael Mascagni，Ashok Srinivasan.Algorithm 806:SPRNG:a scalable library for pseudorandom number generation［J］.ACM Transactions on Mathematical Software，2000，26(3):436－461.

［9］ Thomas Bradley，Jacques Toit，Mike Giles，et al.Parallelisation techniques for random number generators［M］.USA:GPU Gems Emerald，2011.

［10］Wang Endong，Zhang Qing，Shen Bo，et al.High－performance computing on the intel xeon phi－how to fully exploit MIC architectures［M］.China:China Water Power Press，2012.

［11］Shameem Akhter，Jason Roberts.多核程序设计技术—通过软件多线程提升性能［M］.北京:电子工业出版社，2007.

［12］周伟明.多核计算与程序设计［M］.武汉:华中科技大学出版社，2009.

［13］George Marsaglia.The marsaglia random number CDROM including the diehard battery of tests of randomness［EB/OL］.(1995－09－10)［2014－09－12］http://www.stat.fsu.edu/pub/diehard.

［14］L'Ecuyer P，Simard R.TestU01:a clibrary for empirical testing of random number generators［J］.ACM Transactions on Mathematical Software，2007，33(4):22－26.