机械合金化制备Al-Pb纳米相复合结构的热力学分析

吴志方，周 帆，周 ，吴 润



机械合金化制备Al-Pb纳米相复合结构的热力学分析

吴志方1, 2，周 帆1, 2，周 1, 2，吴 润1, 2

(1. 武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，武汉 430081；2. 武汉科技大学耐火材料与冶金国家重点实验室，武汉 430081)

参考Miedema半经验公式，建立Al-Pb系机械合金化过程的热力学模型，并对所制备的Al-10%Pb粉末进行热力学计算和对比分析。实验表明利用机械合金化方法可以获得在Al基体上均匀弥散分布着纳米相Pb的复合结构；热力学计算结果表明，Al-Pb系粉末机械合金化过程不具备形成非晶相、固溶体和中间化合物的热力学驱动力。采用X射线衍射仪(XRD)和扫描电子显微镜(SEM)分析Al-10%Pb合金在高能球磨过程中的组织结构，表明，所建立的热力学模型是正确的。

机械合金化；热力学；Al-Pb合金；纳米相复合结构

机械合金化(mechanical alloying，简称MA)是指利用机械能的作用使材料的组元在常温下实现合金化的材料制备技术[1]。实现机械合金化的方法有高能球磨、复合轧制、高速挤压等，其中高能球磨的应用最为广泛。在机械合金化过程中，由于高能量机械能的作用，材料发生一系列的显微组织结构变化和非平衡态相变，导致各类非平衡态结构的形成，如过饱和固溶体[2−3]、非晶[4]、纳米相复合结构[5−6]等。对MA过程进行热力学计算，有助于认识MA的微观本质，同时也能为设计MA合金提供理论依据。

Al-Pb体系为典型的互不溶体系。由于Al和Pb互不溶，且密度和熔点均相差甚大，采用通常的熔炼方法制备该合金会出现严重的偏晶现象。而采用高能球磨方法制备的Al-Pb合金可以克服上述困难，制备出组织均匀、细小、弥散的Al-Pb纳米相复合结构[7−8]。本研究参照Miedema半经验理论，试建立Al-Pb系MA过程的热力学模型，对Al-10%Pb(质量分数)MA粉末进行具体的热力学计算，并和实验结果进行对比分析，以期为今后的机械合金化提供一定的理论依据。

1 实验

将纯度为99.9%，粒度为75mm的Al、Pb粉按Al-10%Pb(质量分数)成分配成混合粉末。机械合金化在QM-3SP2型行星式高能球磨机上进行，采用淬火钢球和不锈钢罐，球料比为10:1，转速为300 r/min，装样、取样和球磨均在氩气保护下进行。用Philips MPD X’Pert X射线衍射仪(Cu靶材/Kα辐射)和FEI-Navo Nano SEM 400扫描电镜分析合金的组织结构。

2 结果与讨论

2.1 机械合金化制备Al-Pb纳米相复合结构

图1为Al-10%Pb合金粉末球磨不同时间后的XRD图。由图可见，球磨后只有Al和Pb相的衍射峰，且衍射峰的峰位没有偏移。说明没有非晶相和中间化合物形成。从图中还可以看出，随球磨时间延长，Al和Pb相的衍射峰逐渐宽化，这是由于Al和Pb相在球磨中的晶格畸变和晶粒细化所致。利用最小二乘法计算Al的晶格常数，发现球磨25 h后Al的晶格常数基本不变，即机械合金化并没有使Al和Pb两相发生明显的固溶度扩展。因而，纳米相Pb倾向于以第二相弥散地分布在纳米晶Al基体上。

图1 Al-10%Pb合金粉末球磨不同时间后的XRD图

根据衍射峰的宽化情况，利用Vogit函数法[9]计算出球磨不同时间后Al和Pb相的晶粒尺寸，结果如图2所示。从图中可以看出，在球磨初期，Al和Pb相的晶粒尺寸急剧减小；随球磨时间延长，Al和Pb相的晶粒尺寸开始趋于稳定，且Pb相的晶粒尺寸小于Al相的晶粒尺寸。球磨25 h后，Al和Pb相的平均晶粒尺寸分别为45 nm和11 nm。说明采用机械合金化方法在Al-10%Pb合金中获得了纳米相复合结构。

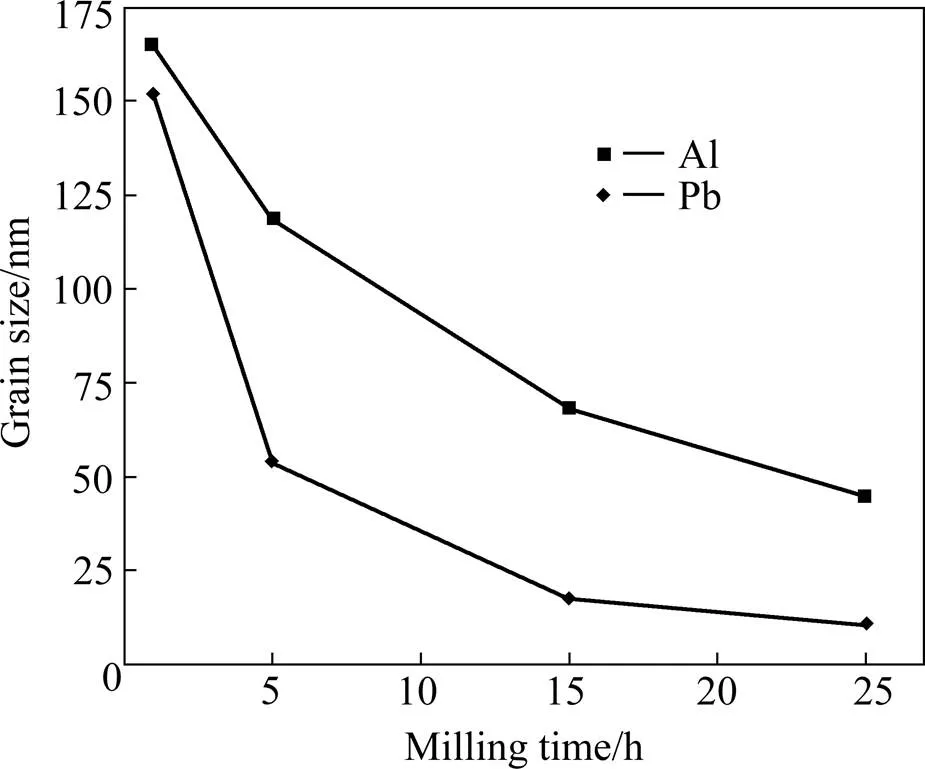
图2 Al-10%Pb合金粉末中Al和Pb相的晶粒尺寸随球磨时间的变化

图3所示为Al-10%Pb合金粉末球磨15 h后的SEM背散射电子像。白亮的组织对应于原子序数大的相，即Pb相，基体相则是Al。由图可见，球磨15 h后，Pb相在Al基体中弥散分布。可见尺寸为数百纳米的Pb颗粒，但一些Pb颗粒的尺寸非常细小，超过了SEM的分辨率。

图3 Al-10%Pb合金粉末球磨15 h后的SEM背散射电子像

2.2 热力学分析

系统的吉布斯自由能变化一般表达为：

Δ=Δ−Δ(1)

式中：Δ和Δ分别为系统的焓变和熵变。LOPEZ及ALONSO[10]等利用Miedema关于系统焓变的生成热模型对系统的熵变作了一些近似，给出了二元合金系统的吉布斯自由能的计算方法。

2.2.1 熵变的计算

LOPEZ及ALONSO[10]只考虑位形变化对合金熵变的影响。对于固溶体和非晶态合金，取一级近似，其混合熵变可写为：

Δ=−(AlnA+BlnB) (2)

式中：A和B分别为合金元素A和B的相对原子含量，A+B=1；为气体常数。

对于中间化合物，由于其原子的有序排列，熵变很小，可以忽略不计。

2.2.2 焓变的计算

根据MIEDEMA的理论[11−12]，LOPEZ及ALONSO等将系统的焓变写为：

Δ=Δc+Δe+Δs(3)

式中：右边3项分别为化学项、弹性项和结构项，分别与合金元素之间的电子分布差异、尺寸差异、结构差异相关。对每一项，LOPEZ及ALONSO等都给出了详细的算法。

(1) 焓变的化学项

1) 稀溶液中的二元合金

对于分别由两种非过渡族金属(Al、Pb均为非过渡族金属)所形成的二元合金系统，金属A溶于B的溶解热为[11−12]：

(4)

式中：和均为经验参数，值取为10.6，下角标ws代表Wigner-Seitz，由于(式中..代表任意的密度单位)，根据值可计算出值为99.64。和分别为纯组元A和B的电子化学势 (*号是有别于实验得出的电负性数值，是经过调整的电负性数值)；和分别为纯金属A和B的Wigner-Seitz原胞边界上的电子浓度。A为纯金属A的摩尔体积。

应当指出的是，当A原子和B原子形成合金时，其原子体积将会发生一定的变化，在计算时，这部分变化应当考虑在内。一般情况下，A原子在合金内的体积为：

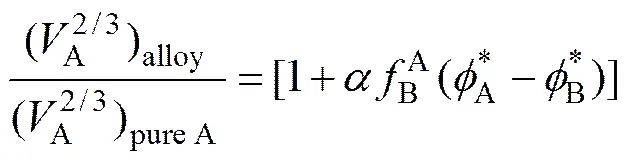
式中：α是一个经验常数，随元素的原子价不同而取值不同。对于碱金属组成的合金，其值为0.14；对于2价金属组成的合金，其值为0.10；对于由贵金属和3价金属组成的合金，其值为0.07；对于其它情况，其值为0.04。在本计算中，α值取为0.04。

式中：为表征合金中化学短程有序度的参量。一般情况下，对固溶体，=0；对中间化合物，=8；对非晶态合金，=5；代表表面，定义A原子和B原子的表面浓度为和，且由下式计算：

(7a)

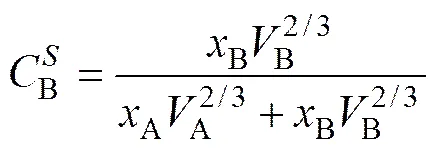
2) 任意浓度溶液中的二元合金

对于1 mol的A，B原子组成的固溶体，由于功函数的差异和原子胞边界电子浓度的差异而引起的变化对系统焓变的影响为：

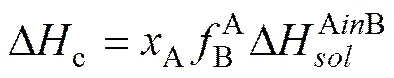
(2) 焓变的弹性项

由于A原子和B原子的大小不同，当它们形成合金时将会导致晶格畸变。晶格畸变会产生弹性能，从而增加合金的焓变。这种由原子的尺寸差异引起的弹性能可以根据“球洞”模型计算。该模型假设在基体B上有一个体积为A的球形洞，被体积为A的原子A所填充。剩余的体积(B−A)将会由于基体和包含物发生弹性应变而消失。该应变引起的弹性能由下式 计算：

式中：A为组元A的体积弹性模量；ΔA和ΔB分别为内部压力引起的“球”和“洞”的体积变化。利用连续弹性介质模型，可以得到1 mol溶质在基体中引起的弹性能为：

(10)

式中：B为组元B的切变模量。

因为在合金化过程中，组分金属的体积要发生相应的变化，A将不同于A。由合金化引起的基体和溶质的体积变化可用下式表示：

(11b)

由于A原子和B原子之间存在尺寸失配，当二者形成合金时将会产生弹性应变。该应变产生的弹性应变能对系统焓变的影响为：

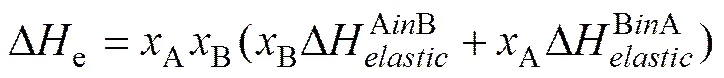
对于非晶态合金和中间化合物不用考虑弹性能，主要是因为非晶态合金中无长程序，谈不上点阵失配；在中间化合物中，由于原子的长程有序排列，可以将原子长程差异引起的点阵畸变减小到可以忽略的程度。因此，弹性项部分的计算主要是针对固溶体而言。

(3) 焓变的结构项

结构项Δs主要是针对过渡族元素间的合金，考虑的是元素A和B原子合金化前后价电子与晶体结构差别对形成焓的贡献。对非过渡族元素组成的合金而言，其结构项为零。

综上所述，对于二元合金固溶体：

对于中间化合物：

(14)

对于非晶态合金[13]：

式中：δ为经验常数，其值为3.5 J/(mol·K)；m, i为金属的熔点，单位为K；0为室温。

机械合金化过程中的温升一般为100~120 ℃，最高为215 ℃[1]，计算温度取400 K。基于上述推导，计算了在400 K时Al-Pb合金的自由能−成分曲线，计算所需的参数列于表1，计算结果如图4所示。从图中可以看出，形成非晶相、固溶体和中间化合物的自由能在Pb的百分含量的全成分范围内均大于零，从热力学驱动力角度讲，Al-Pb合金不易形成非晶相、固溶体和中间化合物。这与实验结果相吻合。

图4 Al-Pb合金形成自由能在T=400 K的计算值

表1 热力学计算用参数

3 结论

1) 利用机械合金化方法可以获得在Al基体上均匀弥散分布着纳米相Pb的复合结构。

2) 热力学计算结果表明，Al-Pb系粉末机械合金化过程不具备形成非晶相、固溶体和中间化合物的热力学驱动力。

3) 热力学计算与实验结果的一致性，表明所建立的热力学模型基本正确。

REFERENCES

[1] SURYANARAYANA S. Mechanical alloying and milling [J]. Progress in Materials Science, 2001, 46: 1−184.

[2] GUDURU R K, SCATTERGOOD R O, KOCH C C, et al. Mechanical properties of nanocrystalline Fe-Pb and Fe-Al2O3[J]. Scripta Materialia, 2006, 54: 1879−1883.

[3] MOJAHEDI M, GOODARZI M, ABOUTALEBI M R, et al. Investigation on the formation of Cu-Fe nano crystalline super-saturated solid solution developed by mechanical alloying [J]. Journal of Alloys and Compounds, 2013, 550: 380−388.

[4] GAFFET E, LOUISON C, HARMELIN M, et al. Mestastable phase transformations induced by ball-milling in the Cu-W system [J]. Materials Science and Engineering A, 1991, 134: 1380−1384.

[5] SELVAKUMAR N, VEYYIVEL S C. Thermal, electrical and wear behavior of sintered Cu-W nanocomposite [J]. Materials and Design, 2013, 46: 16−25.

[6] 史昆玉, 沈 涛, 陈春浩, 等. 高能球磨制备Cu-Cr纳米晶粉末[J]. 粉末冶金材料科学与工程, 2013, 18(4): 532−538.SHI Kun-yu, SHEN Tao, CHEN Chun-hao, et al. Cu-Cr nanocrystalline powder prepared by high-energy ball milling [J]. Materials Science and Engineering of Powder Metallurgy, 2013, 18(4): 532−538.

[7] SHENG H W, LU K, MA E. Melting and freezing behavior of embedded nanoparticles in ball-milled Al-10wt%M (M=In, Sn, Bi, Cd, Pb) mixtures [J]. Acta mater, 1998, 46(14): 5195−5205.

[8] ZHU M, GAO Y, CHUNG C Y, et al. Improvement of the wear behaviour of Al-Pb alloys by mechanical alloying [J]. Wear, 2000, 242: 47−53.

[9] LANGFORD J I. A rapid method for analysing the breadths of diffraction and spectral lines using the Vogit function [J]. Journal of Applied Crystalline, 1978, 11: 10−14.

[10] LOPEZ J M, ALONSO J A, GALLEGO L J. Determination of the glass-forming concentration range in binary alloys from a semiempirical theory: application to Zr-based alloys [J]. Physical Review B, 1987, 36: 3716−3722.

[11] de BOER F R, BOOM R, MATTENS W C M, et al. Cohesion in Metals [M]. North-Holland, Amsterdam, 1988: 63.

[12] MIEDEMA A R. Cohesion in alloys-fundamentals of semi-empirical model [J]. Physica B, 1980, 100: 1−28.

[13] ALONSO J A, GALLEGO L J, LOPEZ J M. Glass formation in binary alloy system: a prediction of the composition range [J]. Philosophical Magazine A, 1988, 58: 79−92.

(编辑 高海燕)

Thermodynamic analysis of Al-Pb nanophase composite prepared by mechanical alloying

WU Zhi-fang1, 2, ZHOU Fan1, 2, ZHOU Yan1, 2, WU Run1, 2

(1. Key Laboratory for Ferrous Metallurgy and Resources Utilization of Ministry of Education, Wuhan University of Science and Technology, Wuhan 430081, China; 2. The State Key Laboratory of Refractories and Metallurgy, Wuhan University of Science and Technology, Wuhan 430081, China)

A thermodynamic model of mechanical alloying of Al-Pb system was established based on Miedema semi-experimental theory for guiding the preparation of Al-10%Pb mechanical alloying (MA) and thermodynamic calculation and analysis. Experiment shows that the Al-Pb nanophase composite alloy in which Pb particles dispersed into the Al matrix has been prepared by mechanical alloying. The thermodynamic analysis shows that there is no driving force to form amorphous phase, solid solution and intermediate compound. Microstructure of Al-10%Pb alloy during high energy ball milling was characterized by X-ray diffraction (XRD) and scanning electron microscopy (SEM). All of the calculation results are agreed with the experimental results.

mechanical alloying;thermodynamics; Al-Pb alloy; nanophase composite

TB383

A

1673-0224(2015)3-344-05

国家自然科学基金资助项目(51201118)；国家级大学生创新创业训练计划项目(201210488023)；清洁能源材料广东省普通高校重点实验室资助项目(KLB11003)

2014-06-10；

2014-09-11

吴志方，副教授，博士。电话：13212756977；E-mail: wuzhifang@wust.edu.cn