高速剑杆织机打纬机构运动精度可靠性分析与计算
唐雪梅,巫世晶,朱伟林,赖奇暐,何 佳
(1.武汉大学 动力与机械学院,武汉 430072;2.武汉纺织大学 机械工程与自动化学院,武汉 430073)
高速剑杆织机打纬机构运动精度可靠性分析与计算
唐雪梅1,2,巫世晶1,朱伟林1,赖奇暐1,何 佳1
(1.武汉大学 动力与机械学院,武汉 430072;2.武汉纺织大学 机械工程与自动化学院,武汉 430073)
针对国产高速剑杆织机可靠性、稳定性、运动精度等急待提高的难题,基于考虑基本尺寸误差、运动副间隙误差及凸轮副表面磨损误差时共轭凸轮打纬机构运动精度的3种计算模型,建立了打纬机构运动精度可靠性求解的精确解析方程式,并运用Maple数值分析软件进行了仿真计算,揭示了各主要误差因素对高速共轭凸轮打纬机构运动精度可靠性的影响规律.结果表明对高速共轭凸轮打纬机构运动精度可靠性影响程度由大到小依次为:凸轮副表面磨损误差、基本尺寸误差、运动副间隙误差,并提出了提高共轭凸轮打纬机构运动精度可靠性的具体措施.
高速剑杆织机;打纬机构;运动精度可靠性;共轭凸轮;可靠性指标;Maple
我国纺织业在提升国力、推动国民经济全面协调发展等方面做出了难以估量的贡献[1].在剑杆织机中,高档机型有90%以上都是国外进口.打纬机构是剑杆织机中的关键部件,它的运动性能直接决定织物的质量、织机的质量和效率.现代织机大多采用共轭凸轮打纬机构[2].共轭凸轮机构是一个闭环尺寸链,其主、副凸轮共同作用驱动摆杆作往复摆动,由于这种尺寸间的闭合关系,使得从动件的滚子与凸轮表面保持接触,实现精确的运动传递,并维持平稳运行.然而,由于误差的存在,当主凸轮表面与滚子接触时,副凸轮表面与滚子间总会存在间隙或干涉,间隙太大会产生冲击、振动与噪音,而干涉过大则会造成机构的运动被卡住,甚至不能安装[3].共轭凸轮机构的加工精度与性能要求较高,国内加工的共轭凸轮机构性能均较差,很难满足剑杆织机的高速运转要求.目前,在高档剑杆织机中,高精度的共轭凸轮机构几乎都是从国外进口.而国外的相关文献中很少有实质性内容,关键技术均掌握在国外一些专业的凸轮制造商和科研机构手中.国产剑杆织机的最大症结就是制造质量与可靠性问题.随着机械向高速化、高精度化、高智能化方向发展,结构可靠性的研究已不能满足高端科技的要求,而机构运动精度可靠性的研究越来越受到重视[4-6].本文以剑杆织机共轭凸轮打纬机构为对象,进行机构运动精度可靠性研究,找出各因素的影响规律,提出改进措施提高机构运动精度可靠性.
1 共轭凸轮打纬机构运动精度可靠性求解
在影响凸轮机构从动件位置误差的众多因素中,基本尺寸、运动副间隙和凸轮副表面磨损是比较突出的影响因素,本文主要从这三方面误差考虑,对共轭凸轮打纬机构运动精度可靠性进行分析计算.根据文献[7]中建立的打纬机构数学模型,以及由该模型推导出的打纬机构输出摆角φ对于凸轮转角θ以及机构基本尺寸的关系式,可建立输出参数打纬摇轴的摆角在各误差因素影响下随凸轮转角变化的运动精度可靠性数学模型.
1.1 考虑基本尺寸误差的打纬机构运动精度可靠性分析
打纬机构基本尺寸误差主要有:主、副凸轮轮廓线加工误差Δx、Δy;摇轴摆杆长度加工误差Δl;摇轴摆杆安装误差Δa以及滚子半径加工误差Δr.当取一组相同机构考虑时,基本参数x、y、l、a、r均可作为随机变量,并一般都服从正态分布[8].由文献[7]可知打纬机构摆角误差与各基本尺寸误差之间的函数关系式,因此,在打纬机构中由这些基本参数误差所引起的打纬机构输出摆角位置误差Δφ1的均值与方差可分别表示为:

式中:E(*)表示随机变量的均值;D(*)表示随机变量的方差.
假设给定打纬机构输出摆角的允许极限总误差为Δ,也是一个随机变量,并服从正态分布,其均值与方差分别为μΔ和σ2Δ.根据一次二阶矩法和可靠性理论[9-11],考虑基本尺寸误差时打纬机构运动精度可靠性指标β为:

1.2 考虑运动副间隙误差的打纬机构运动精度可靠性分析
文献[7]中根据“有效长度理论”,详细给出了打纬机构输出摆角位置误差在运动副间隙误差影响之下的计算表达式.取一组相同机构考虑时,其基本参数即主凸轮与支座间铰链的销轴中心局部坐标xo1、yo1和滚子与摆杆间铰链的销轴中心局部坐标xo3、yo3均属于随机变量,通常都服从正态分布,摆杆与支座之间的铰链误差可不计.当已知各运动副的配合公差带时,运动副间隙的均值与标准差可由3σ原则来确定[12-14].所以由运动副间隙所引起的打纬机构摆角位置误差Δφ2的均值与方差分别为:

考虑运动间隙误差时打纬机构运动精度可靠性指标β为:

1.3 考虑凸轮副表面磨损误差的打纬机构运动精度可靠性分析
考虑凸轮副表面磨损时,根据转换机构法,打纬机构输出摆角位置误差的表达式如文献[7],考虑一组相同机构时,共轭凸轮打纬机构在2个凸轮副处的磨损量Δw1和Δw2都为随机变量,且通常服从正态分布.与前面推导类似,由凸轮副表面磨损所引起的打纬机构摆角位置误差Δφ3的均值与方差可分别表示为:
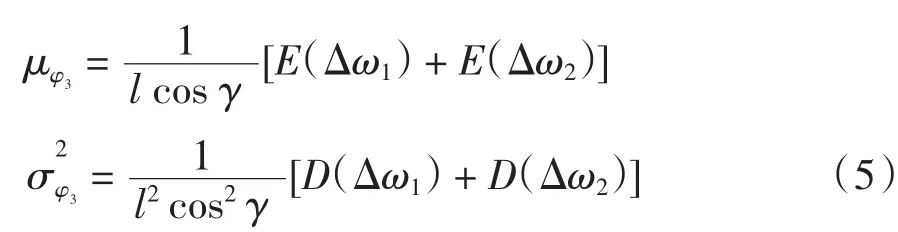
考虑凸轮副表面磨损误差时打纬机构运动精度可靠性指标β为:

1.4 打纬机构运动精度可靠性计算模型
考虑到制造工艺与加工方式的不同,机构中各基本尺寸误差、各运动副间隙以及由凸轮副表面磨损所带来的误差,可以被看作是彼此相互独立的,并且这些误差跟机构各名义尺寸相比较都是微小量.因此,可以对基本尺寸误差、运动副间隙误差与凸轮副表面磨损误差各自所造成的机构运动输出误差分别进行求解,然后将各项叠加来求解机构输出的总误差[15-16].综合考虑以上分析的3种误差时,引起的打纬机构输出摆角位置总误差Δφ可表示为:

考虑一组相同机构时,以上3项误差均为相互独立的随机变量,假设其中各参数都服从正态分布,那么机构总误差Δφ的均值与方差分别为:

因此,综合考虑基本尺寸误差、运动副间隙误差及凸轮副表面磨损3种误差时,打纬机构运动精度可靠性指标β为:

可靠度R为:

式中:φ(*)指标准正态分布函数.
2 共轭凸轮打纬机构运动精度可靠性实例分析
某高速剑杆织机共轭凸轮打纬机构,设计转速为600 r/min,中心距a为128 mm,摆杆的最大摆角h为24°,打纬推程角φ1和回程角φ2均为70°,给出基圆的初始半径rb为90 mm,滚子半径r为30 mm,两摆杆长度l1、l2均为60 mm,推程和回程采用摆线运动规律,其详细轮廓曲线方程如表1所示.
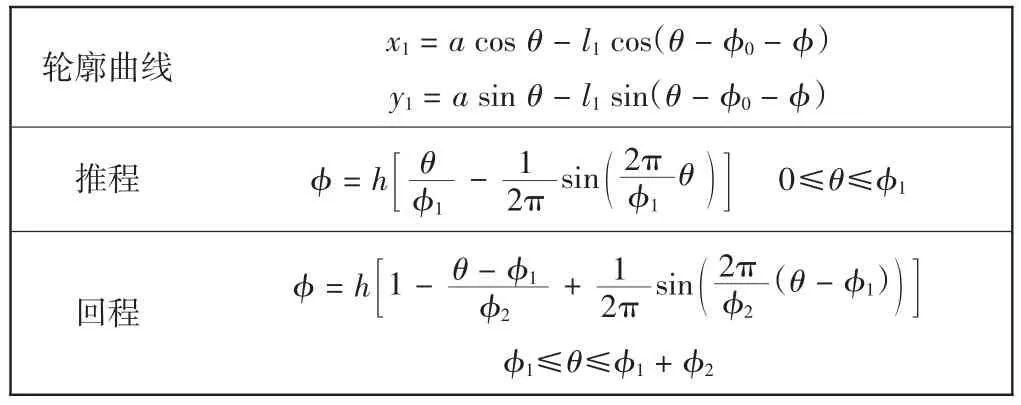
表1 共轭凸轮打纬机构主凸轮轮廓方程Tab.1 Profile equation of main cam in conjugate cam beating-up mechanism
由文献[7]得出的结论以及共轭凸轮机构主、副凸轮的共轭特性可知,对主凸轮机构进行分析计算得出的运动精度可靠性即是共轭凸轮打纬机构运动精度可靠性结果.
2.1 不同误差因素对打纬机构运动精度可靠性的影响
采用上述方法对主凸轮机构分别考虑机构基本尺寸、运动副间隙和凸轮副表面磨损3种误差的情况下,进行机构运动精度可靠性分析计算,可求得综合上述3种误差影响因素打纬机构输出运动精度可靠性指标和可靠度,结果如表2所示.运用Maple软件进行数学仿真,得出打纬摇轴摆角运动精度可靠度随凸轮转角变化的曲线图,如图1—图3所示.

表2 共轭凸轮打纬机构运动精度可靠性指标及可靠度Tab.2 Kinematics accuracy reliability index and reliability of conjugate cam beating-up mechanism

图1 考虑基本尺寸误差时运动精度可靠度变化曲线图Fig.1 Curve of kinematics accuracy reliability considering dimension errors
对以上计算结果分析可知,打纬机构的运动副间隙误差对机构运动精度可靠性影响相对较小,整个周期内摇轴摆角误差的运动精度可靠度最低值接近0.981 9;其次是基本尺寸误差的影响,而凸轮副表面磨损误差对机构运动精度可靠性的影响在整个周期内均比较大,摇轴摆角误差的运动精度可靠度最低值接近0.963,且随凸轮转角的变化波动较大.

图2 考虑运动副间隙误差时运动精度可靠度变化曲线图Fig.2 Curve of kinematics accuracy reliability considering clearances errors of hinged joints
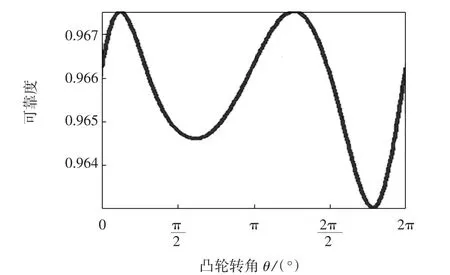
图3 考虑凸轮副表面磨损误差时运动精度可靠度变化曲线图Fig.3 Curve of kinematics accuracy reliability considering cam surface wear errors
2.2 各误差因素的均值与方差对打纬机构运动精度可靠性的影响
为了更深入地研究打纬机构中各误差的变化对打纬机构输出运动精度可靠性的影响规律,提出具体措施来指导共轭凸轮打纬机构的设计制造,现利用软件进一步对打纬机构运动精度可靠性进行数字仿真.采用相同量值的改变各误差的均值,即公差带中心的位置,将各基本尺寸误差均值增加或减小0.01 mm,运动副间隙误差均值增加或减小0.1 mm,凸轮副磨表面损误差均值增加或减少0.1 mm,仿真计算得出分别考虑3种误差时打纬机构运动精度可靠度的结果曲线如图4—图9所示.

图4 减小各尺寸误差均值的结果曲线Fig.4 Result curve of reducing the mean of dimension errors
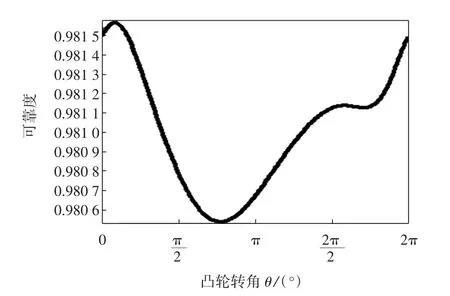
图5 增加各尺寸误差均值的结果曲线Fig.5 Result curve of increasing the mean of dimension errors
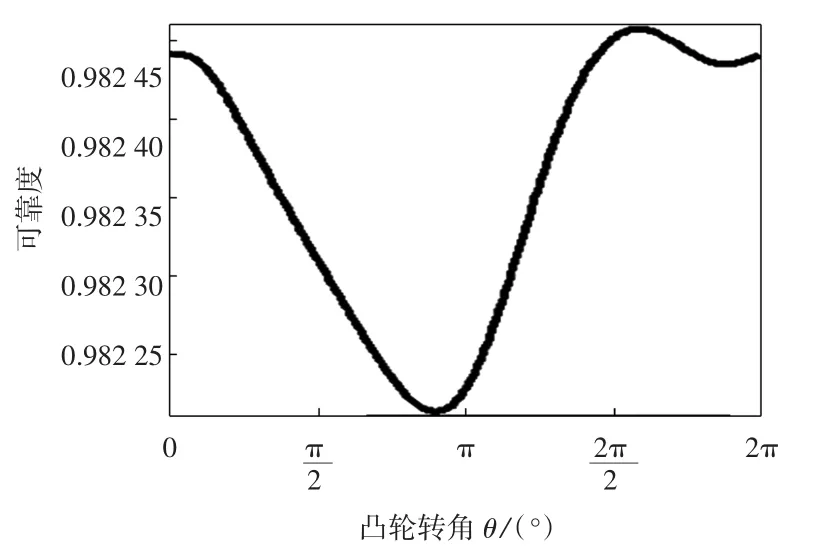
图6 减小运动副间隙误差均值的结果曲线Fig.6 Result curve of reducing the mean of clearances errors of hinged joints

图7 增加运动副间隙误差均值的结果曲线Fig.7 Result curve of increasing the mean of clearances errors of hinged joints
将图4,图5与图1进行对比可知,随着各基本尺寸误差均值的减小,打纬机构运动精度可靠度由0.980 6~0.981 6升高到0.980 7~0.981 7之间;随着各尺寸误差均值的增加,打纬机构运动精度可靠度则降低至0.980 5~0.981 55之间.

图8 减小凸轮副表面磨损误差均值的结果曲线Fig.8 Result curve of reducing the mean of cam surface wear errors

图9 增加凸轮副表面磨损误差均值的结果曲线Fig.9 Result curve of increasing the mean of cam surface wear errors
对比图6、图7与图2可知,减小运动副间隙误差均值,打纬机构运动精度可靠度由0.9819~0.9824升高到0.982 21~0.982 46之间;增加运动副间隙误差均值,打纬机构运动精度可靠度则降低至0.981 4~0.982 35之间.
对比图8、图9与图3可知,减小凸轮副表面磨损误差均值,打纬机构运动精度可靠度由0.963~0.968升高到0.970 2~0.973 0之间;增加凸轮副表面磨损误差均值,打纬机构运动精度可靠度则降低至0.954~0.962之间.
由此得出结论,在共轭凸轮打纬机构设计制造中,各基本尺寸公差带、运动副间隙公差带、凸轮副表面磨损公差带中心均应向左移.因此,为了提高打纬机构运动精度可靠性,在加工中应尽可能选择负的公差值.
改变各误差的方差,即公差带的宽窄,从3种误差因素来分析均可得出相同结论:减小各误差的方差值,打纬机构运动精度可靠度均相应提高,故公差带应越窄越好.这一结论符合工程实践,同时验证了本方法的正确性.由于篇幅有限,下面仅以改变基本尺寸误差的方差为例加以说明,对比图10、图11与图3可知,减小误差方差,打纬机构运动精度可靠度由0.980 6~0.981 6升高到0.981 2~0.981 95之间;增加基本尺寸误差方差,打纬机构运动精度可靠度则降低至0.970 9~0.981 3之间.
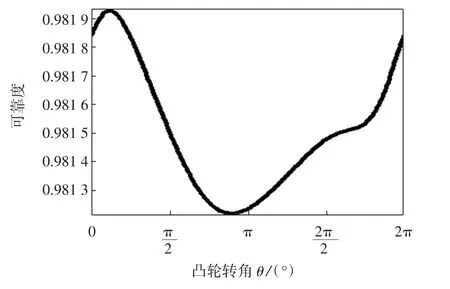
图10 减小基本尺寸误差方差的结果曲线Fig.10 Result curve of reducing the variance of dimension errors
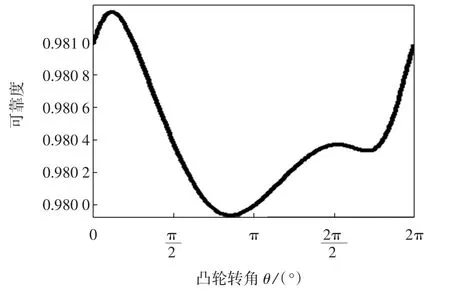
图11 增加基本尺寸误差方差的结果曲线Fig.11 Result curve of increasing the variance of dimension errors
3 结论
对共轭凸轮打纬机构进行了运动精度可靠性分析与计算,应用Maple软件进行仿真分析,分析结果表明:
(1)在所考虑的3种主要误差中,对打纬机构运动精度可靠性影响程度由大到小依次为:凸轮副表面磨损误差、基本尺寸误差、运动副间隙误差.高速剑杆织机设计中,可按此顺序控制各误差的大小以提高运动精度可靠性.
(2)经过进一步分析可知,增加各类误差均值,打纬机构运动精度可靠度降低;减小各误差均值,打纬机构运动精度可靠度升高.因此,在共轭凸轮打纬机构设计制造中,各基本尺寸公差带、运动副间隙公差带、凸轮副表面磨损公差带中心均应向左移.在共轭凸轮打纬机构加工制造中应尽可能选择负的公差值,可以提高打纬机构运动精度可靠性.
(3)减小各误差方差值,打纬机构运动精度可靠度相应升高,故各误差的公差带越窄越好,符合工程实践.
[1] 高顺成.中国纺织业对国民经济发展的贡献研究[J].纺织学报,2014,35(7):145-151.
[2]郑智毓.TT96型剑杆织机打纬机构分析[J].纺织学报,2004,25(6):116-117.
[3] 石书义.平面共轭凸轮共轭精度的分析 [J].纺织机械,2002,15(2):46-48.
[4] 王西珍,李言,成刚虎.柴油机主运动机构运动精度可靠性算法[J].农业工程学报,2011,27(4):184-189.
[5]WANG Jinge,ZHANG Junfu,DU Xiaoping.Hybrid dimension reduction for mechanism reliability analysis with random joint clearances[J].Mechanism and Machine Theory,2011,46(46):1396-1410.
[6]CHEN Lijie,LI Zhenzhou,WANG Qi.A study of the mechanism kinematics accuracy reliability by probability density evolution method [J].Mechanical Science and Technology for Aerospace Engineering,2010,5(1):20-29.
[7] 唐雪梅,朱伟林,赖奇暐,等.共轭凸轮打纬机构运动精度分析[J].机电工程,2014,31(2):173-176.
[8]国志刚,冯蕴雯,冯元生.摆动推杆盘形凸轮机构运动精度可靠性分析[J].机械科学与技术,2006,25(2):200-203,228.
[9]孙志礼,陈良玉.实用机械可靠性设计理论与方法[M].北京:科学出版社,2003.
[10]张义民,黄贤振,贺向东.任意分布参数平面连杆机构运动精度可靠性稳健设计[J].农业机械学报,2008,39(7):139-143.
[11]EKINCI T O,MAYER J R R.Relationships between straightness and angular kinematics errors in machines[J].International Journal of Machine Tools and Manufacture,2007,47(12/13):1997-2004.
[12]SU Y X,DUAN B Y.The mechanical design and kinematics accuracy analysis of a fine tuning stable platform for the large spherical radio telescope[J].Mechatronics,2000,10(7):819-834.
[13]赵竹青.机构运动精度可靠性分析与设计[D].西安:西安电子科技大学,2002.
[14]HELLESLAND Jostein.Evaluation of effective length formulas and applications in system instability analysis[J].Engineering Structures,2012,45(5):405-420.
[15]PANDEY Mahesh D,ZHANG Xufang.System reliability analysis of the robotic manipulator with random joint clearances[J]. Mechanism and Machine Theory,2012,58(2):137-152.
[16]ZHOU Yuming,ZHAO Zhuqing.Analysis and numerical simulation on reliability of motion accuracy for planar cam mechanism[J].Journal of Machine Design,2005,22(1):48-50.
Analysis and calculation of kinematics accuracy reliability on beating-up mechanism of high-speed rapier loom
TANG Xue-mei1,2,WU Shi-jing1,ZHU Wei-lin1,LAI Qi-wei1,HE Jia1
(1.School of Power and Mechanical Engineering,Wuhan University,Wuhan 430072,China;2.School of Mechanical Engineering and Automation,Wuhan Textile University,Wuhan 430073,China)
The reliability,stability and kinematics accuracy of domestic high-speed rapier loom were urgent to be improved. Based on the kinematics accuracy models of conjugate cam in beating-up mechanism considering the three errors including dimension errors,clearances of hinged joints and cam surface wear error,the precise analytic equation for the solution of kinematics accuracy reliability of beating-up mechanism was established.And the simulation was carried out using Maple software.The influence of the major factors on kinematics accuracy reliability of highspeed conjugate cam beating-up mechanism was revealed systematically.The results show that the descending order of influence degree for the kinematics accuracy reliability of high-speed conjugate cam beating-up mechanism is cam surface wear error,dimension errors,clearances error of hinged joints.The specific measures of improving kinematics accuracy reliability of conjugate cam in beating-up mechanism are put forward.
high-speed rapier loom;beating-up mechanism;kinematics accuracy reliability;conjugate cam;reliability index;Maple
TS103.337.3;TH112
A
1671-024X(2015)01-0078-06
2014-10-31
国家自然科学基金资助项目(51375350)
唐雪梅(1983—),女,博士,讲师,主要研究方向为机械数字化设计、机械动力学.E-mail:xmtang_2000@163.com

