单纯形-入侵杂草算法在阵列天线波束赋形的应用
梁 静,李朝伟,2,陈智慧,2,樊小景,2
(1 中国空空导弹研究院,河南洛阳 471009;2 航空制导武器航空科技重点实验室,河南洛阳 471009)
单纯形-入侵杂草算法在阵列天线波束赋形的应用
梁 静1,李朝伟1,2,陈智慧1,2,樊小景1,2
(1 中国空空导弹研究院,河南洛阳 471009;2 航空制导武器航空科技重点实验室,河南洛阳 471009)
针对入侵杂草算法在全局搜索过程中收敛速度慢的问题,文中提出基于单纯形的入侵杂草算法,并将该改进算法应用于阵列天线波束赋形中。单纯形-入侵杂草算法是利用单纯形局部搜索能力强,收敛速度快的特性,在平衡入侵杂草算法全局和局部寻优能力的同时,提高入侵杂草算法的收敛速度和计算精度。优化结果表明,与基本入侵杂草相比,该改进算法在阵列天线波束赋形中性能更佳。
波束赋行;入侵杂草算法;单纯形搜索法
0 引言
近年来,阵列天线被广泛应用于军事、通信、天文等领域,为了在不同的工作环境实现特定的某些功能,需要阵列天线具有特殊形状的天线波束(如笔形波束、扇形波束、余割波束等)功能。阵列天线波束赋形是根据给定的波束形状求解阵列天线的某些参数(比如激励、位置),使阵列天线的辐射特性满足给定的要求。阵列天线波束赋形是一个多参数,非线性优化问题,传统解析优化方法如Dolph-Chebyshev,Taylor[1]等是针对某些特定问题的求解方法,但对于有约束条件或复杂要求的优化问题,无法得到工程中的有效结果。随着智能计算机技术的发展,应用智能优化算法对阵列天线进行波束赋形已成为研究的热点。常见的智能算法如差分进化算法[2](GA)、遗传算法[3](PSO)等因其良好的鲁棒性在阵列天线波束赋行中得到了广泛的应用。文中采用入侵杂草优化(invasive weed optimization,IWO)算法,以天线阵元的激励为优化变量,实现阵列天线方向图的赋形。
入侵杂草算法[4]是一种受杂草启发而提出的、基于种群的数值优化计算方法,由伊朗德黑兰大学的A.R.Mehrabian以及C.Lucas在2006于Ecological Informatics杂志上提出。该算法执行过程是模拟杂草入侵过程的算法,具有结构简单,收敛速度快,鲁棒性强,易于理解和易于编程等特点,已经被成功的应用于许多领域[5]。为了解决IWO的寻优过程中没有利用当代种群的信息,个体之间没有交流的问题,文中利用单纯形搜索法(simplex method)对杂草处理,使得杂草有方向性的向当代较好的个体移动,这种改进方法在保证种群个体的多样性的同时,也提高了入侵杂草算法的寻优速度,达到优势互补的效果。仿真结果显示,基于单纯形的入侵杂草算法在收敛性能方面优于基本的入侵杂草算法。
1 基于单纯形的入侵杂草算法
入侵杂草算法是一种模拟杂草繁殖过程的全局优化方法,其优化过程包括杂草克隆、占地生长与繁殖。在基本IWO算法中,杂草代表产生的随机可行解,种群是全部杂草的集合,而种子是杂草产生的子代。产生初始种群后,种群中的杂草个体以适应度函数为标准,计算每个杂草个体产生的新的种子个数,产生的种子以正态分布的分布方式叠加在父代周围,并占领殖民地。对殖民地中的每一个种子,根据适应度函数计算它的适应度值,此时种子成为成熟的杂草个体。这些成熟的子代和父代个体共同形成新的种群。当新种群中个体数目大于种群能够接受的个体数目上限Pmax时,只留下Pmax个具有最佳适应度值的个体,较差的杂草个体被剔除。随后,新的种群重复以上过程,直到种群中最优个体的适应度值和最差个体的适应度值差值很小,或者进化代数满足预定的值时,把具有最佳适应度值的个体保留下来,算法结束。从入侵杂草算法的优化过程中可以看出,IWO具有适应度为基准的繁殖机制、正态分布的扩散机制和子父代竞争排斥机制,这些机制使得较差的个体也有繁殖的机会,保证了种群个体的多样性。但该算法没有利用当代种群之间的信息,个体之间没有交流,没有考虑变量之间的相关性。为了加快寻优,采用一种无约束最优化的单纯形搜索法法对杂草进行处理。单纯形搜索法[6]是在给定Rn中的一个单纯形后,求出(n+1)个顶点的函数值,确定出有最大函数值的点和最小函数值的点,然后通过反射、扩展、压缩等方法求出一个较好的点,用它取代最高点,构成新的单纯形,或者通过向最低点收缩形成新的单纯形,用这样的方法逼近极小点。基于单纯形的入侵杂草算法的流程图如图1。

图1 基于单纯形的入侵杂草算法流程图
基于单纯形的入侵杂草算法是在IWO第t次迭代后,利用即将进入下一代的个体构造单纯形,经过单纯形搜索法产生新的单纯形作为IWO的第(t+1)次的初始种群。单纯形搜索法每一次迭代只增加一个或两个新点,计算量小,所以即使天线单元数增加,计算量也不会显著增加。
2 适应度函数
在不考虑阵列单元之间耦合的条件下,设所有阵元为理想全向辐射单元,天线阵列的辐射方向图为F。适应度函数的设计需要在赋形的同时,也要根据实际应用环境满足在不同方向的旁瓣电平低于给定限值。假设在不同方向的旁瓣电平为SL1,SL2,…,SLN,则旁瓣区域内实际方向图与期望方向图的误差为:
(1)
式中:F是当前迭代的激励产生的远场方向图;S是给定的期望方向图。则实际方向图与期望方向图总的均方误差为:
(2)
式中:l1,l2,…,lN是不同旁瓣对应的旁瓣采样点数。权重系数ω1,ω2,…,ωN根据情况设定。
3 优化实例
利用2组仿真实例,通过比较基本入侵杂草算法和基于单纯形的入侵杂草算法的波束赋形优化结果,验证该方法的有效性和可行性。
3.1 综合线阵不对称方向图
综合要求:对一个单元数目N=32的均匀线阵,要求在(-π/2,0)的区域旁瓣SL1=-30,在(0,π/2)区域的旁瓣SL2=-17,适应度函数选择如式(2)。d是单元间距,B是主瓣宽度,E是迭代次数,γ是扩展系数,β是压缩系数,参数值参见表1。

表1 均匀线阵的参数值
在相同的参数设置下,基本入侵杂草算法和基于单纯形的入侵杂草算法的优化结果如图2和图3所示。从图3收敛曲线的对比图可以看出,基本的入侵杂草算法在1 800次迭代之后趋于收敛,而基于单纯形的入侵杂草算法在迭代800次的时候已经收敛,由于单纯形的计算量非常小,不会增加优化过程的计算时间,因此,收敛速度提高了2倍,并且基于单纯形的入侵杂草算法实现的波束赋形曲线更为平滑,收敛特性更为稳定。在图3中,基本的入侵杂草算法的最终适应度值优于基于单纯形的入侵杂草算法,根据式(2)可知,为了减少适应度函数的计算量,低于期望旁瓣电平的误差为零。
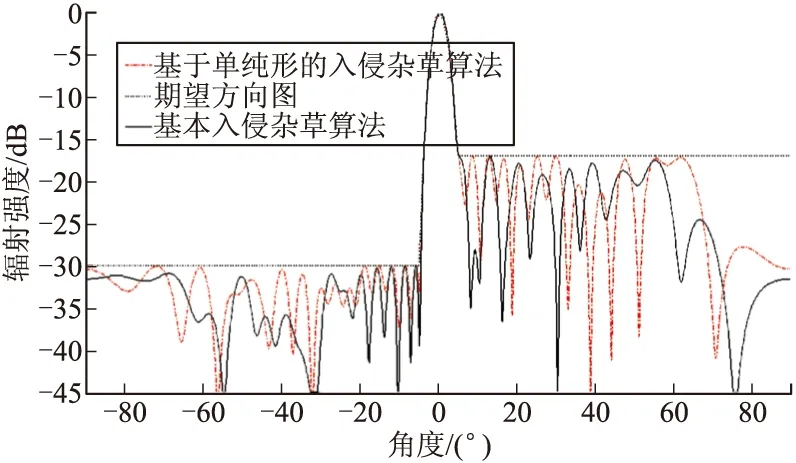
图2 赋形波束比较

图3 收敛曲线对比图
3.2 综合同心圆环阵的笔形波束
综合要求:对于由N=5个同心圆组成的均匀分布圆环阵,相邻单元之间的径向间隔L=λ/2,阵元弧向间距d=λ/2,笔状波束主辐射方向θ=0°,阵元个数M=93。为了减少参数变量,要求圆环阵的每一环上的单元的幅度相同,即优化参量的个数是圆环阵的环数和单元个数的和。具体参数选取参照表2。

表2 参数选取值
在相同参数设置的情况下,基于单纯形的入侵杂草算法与基本的入侵杂草算法对同心圆环阵进行笔形波束赋形,优化结果如图4和图5。由图可见,基于单纯形的入侵杂草算法很好的实现了波束赋形,在相同条件下的波束赋形结果优于基本入侵杂草算法。基本入侵杂草算法没有满足最高旁瓣电平为-30 dB的要求,其赋形结果的最大旁瓣电平是-27.83 dB。而基于单纯形的入侵杂草算法满足旁瓣区域的要求,与期望方向图拟合效果更佳。在图5中,基本入侵杂草算法250次迭代之后曲线收敛,而基于单纯形的入侵杂草算法在迭代100次后收敛,收敛速度提高两倍。

图4 天线波束赋形E面方向图比较

图5 收敛曲线对比图
由以上实例可以看出,基于单纯形的入侵杂草算法的收敛特性明显优于基本的入侵杂草算法。
4 结论
文中将单纯形与入侵杂草算法进行混合,利用单纯形算法收敛速度快的优点指导入侵杂草算法种子的进化方向,提出了一种高效易实现的混合优化算法。全局优化算法与局部优化算法的结合大大提高了收敛速度和收敛精度。最后将该算法成功应用于线阵和圆环天线阵列的波束赋形中。该算法对阵列天线的参数没有任何限制,可用于各种应用要求,下一步致力于研究该算法应用于其他特殊要求的方向图。
[1] 薛正辉, 李伟明. 阵列天线分析与综合 [M]. 北京: 北京航空航天大学出版社, 2011.
[2] MARCANO D, DURAN F. Synthesis of antenna arrays usin g genetic algorithms [J]. IEEE Antennas PropagatMag, 2000, 42(6): 1692-1698.
[3] 陈滕博, 焦永昌, 张福顺. 基于改进型粒子群算法的阵列天线综合 [J]. 微波学报, 2006, 22(增刊): 39-43.
[4] Mehrabian A R, Lucas C. A novel optimization algorithm inspired from weed colonization [J]. Ecological Informatics, 2006, 1(3): 355-366.
[5] Gourab Ghosh Roy, Swagatam Das, Prithwish Chakraborty. Design of non-uniform circular antenna arrays usin g a modified invasive weed optimization algorithm [J]. IEEE Transacyions on Antennas and Propagation, 2011, 59(1): 110-118.
[6] 陈宝林. 最优化理论与算法 [M]. 北京: 清华大学出版社, 2005: 343-348.
Application of SM-IWO in Beam-forming of Array Antennas
LIANG Jing1,LI Chaowei1,2,CHEN Zhihui1,2,FAN Xiaojing1,2
(1 China Airborne Missile Academy, Henan Luoyang 471009, China; 2 Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, Henan Luoyang 471009, China)
For overcoming the problem of slow convergent speed of IWO in global searching, simplex method(SM)-invasive weed optimization (IWO) algorithm was proposed and applicated in beam-forming of array antennas. simplex method(SM)-invasive weed optimization (IWO) algorithm makes a balance between the global and local searching ability, and improves convergent speed by taking advantage of good local searching and fast convergent of SM. Simulation results prove that the improved algorithm has better performance compared with basic IWO.
shaped beam; invasive weed optimization algorithm; simplex method
2014-11-21
梁静(1989-),女,江苏沛县人,硕士研究生,研究方向:电磁场与电磁波。
TN820.12
A

