基于高维插值的末修弹落点预报方法研究

黄 鑫,赵捍东,李志鹏

(中北大学机电工程学院,太原 030051)



基于高维插值的末修弹落点预报方法研究

黄 鑫,赵捍东,李志鹏

(中北大学机电工程学院,太原 030051)

为快速精确的预报弹丸落点,提出了基于高维插值的末修弹落点预报方法。在介绍高维插值法的基础上,以末段弹道参数为离散点,对其高维插值,得到落点预报显示方程,并利用显示方程进行落点预报仿真测试。仿真结果表明,该方法预报落点的精度较高,且平均预报时间为3.508 ms,比数值积分法少709.393 3 ms。因此,采用高维插值法预报落点是有效可行的,可为实际应用提供参考。

落点预报;高维插值法;数值积分法;扩展卡尔曼滤波

0 引言

在现代战争中,精确打击[1]成为弹药发展的主攻方向,而弹丸落点预报的快速与精确性是实现高精度打击的关键技术。

目前,落点预报方法主要有数值积分法、滤波外推法和线性化法等。数值积分法[2]是采用龙格-库塔法实时解算外弹道方程,能准确的预报落点,但在预报过程中,需要繁琐的迭代,这不仅消耗大量的时间且易产生累积误差。滤波外推法[3-5]能降低噪声和随机误差对落点预报的影响,但处理非高斯噪声时,易于发散,达不到准确预报落点的目的。线性化法[6-7]是在一定程度下,将非线性外弹道方程近似化,得到线性方程,利用解析法解算弹道方程。该方法相比于数值积分法,能够快速预报弹丸落点,但在精度上存在不足。因此,为快速精确的预报落点,提出了基于高维插值的末修弹落点预报方法。

1 落点预报方法及滤波介绍

1.1 末修弹落点预报的方法

文中首次提出一种适用于末修弹的落点预报方法,即基于高维插值的落点预报方法。图1所示为该方法预报末修弹落点的示意图。其中,O-xyz表示发射坐标系;“▲”为弹道高的位置,“△”表示高维插值法落点预报的初始点位置,A为弹丸实际落点,B为高维插值法预报的弹丸落点。

从弹丸在弹道高处开始,利用弹载传感器进行弹道参数测量,在设定的时间内,采用扩展卡尔曼滤波算法对弹道参数辨识。并以结束时刻的弹道参数作为预报的初始点,由高维插值法预报弹丸落点。

图1 高维插值法落点预报的示意图

1.2 基于扩展卡尔曼滤波的弹道参数辨识

落点预报时,需通过GPS实时探测与跟踪飞行过程中弹丸的弹道参数,并由扩展卡尔曼滤波算法对弹道参数辨识。

扩展卡尔曼滤波[8]是应用于非线性系统的卡尔曼滤波,其系统方程和量测方程为:

(1)

式中:W(t)为模型噪声;V(t)为量测噪声,且均为高斯白噪声;X为状态向量;f(X)为状态方程。

为预报扩展卡尔曼滤波预测的结果,其迭代公式为:

(2)

其中:

(3)

2 落点预报

2.1 高维插值法

插值法是离散问题解析化的方法之一,所谓插值法,即已知n个离散点(xi,yi),i=1,2,…,n,在某一已知的函数类g(w,x)中,若能找到一个函数g(w*,xi),使其g(w*,xi)=yi,i=1,2,…,n,则称g(w*,xi)为通过此n个点的插值函数。插值函数的构造是插值法的核心问题,目前,一维和二维插值法应用较为常见,插值函数一般采用n次多项式和Hermite插值多项式。但是一维和二维插值法仍是低维插值法,只能处理低维空间的离散点,若对于处理高维空间,低维插值法就不适用了,为此提出高维插值方法。

文中以高斯函数为基底的加权作为插值函数,其数学表达式为:

(4)

式中:γj∈Rm表示第j个离散点;χi∈Rm表示该方程的自变量;yi表示因变量;wj表示第j个权值;φij为高斯函数;‖χi-γj‖为欧式距离,一般为矩阵2范数;δ表示高斯函数的宽度。

若将n组χi∈Rm的离散点代入式(4)中,可得:

(5)

即:

Y=ΦW

(6)

当m维空间中的离散点不同时,则Φ可逆,则有:

W=YΦ-1

(7)

2.2 基于高维插值法的末修弹落点预报

落点预报是实现落点预测制导律的重要一步,其中,落点信息包括射程和横偏。而描述弹丸飞行状态的弹道参数很多,如弹丸位置坐标、速度分量、姿态角等。如何确定离散点的维数是建立落点预报显示方程的关键问题。为保证自变量与因变量有着密切的联系,综合考虑,离散点的维数选为5维,自变量为χi=[xi,zi,vxi,vzi,θi]T,表示当前弹丸的状态参数,其中,xi和zi为弹丸位置分量,vxi和vzi为弹丸速度分量,θi为弹道倾角,而因变量选为弹丸的射程和横偏。则有以下函数关系:

(8)

通过高维插值法可得式(8)的显示方程。由2.1节知,高维插值法是将高维空间中离散点解析化的数学方法,具有原理简单,解算时间快等优点。因此,以射程为例,预报数学模型为:

(9)

式中:Xi表示射程;Wxj表示第j个权值;χxi表示射程预报方程的自变量,其形式为χxi=[xi,zi,vxi,vzi,θ]T,其中,xi、zi表示当前弹丸位置分量,vxi、vyi表示当前弹丸速度分量,θ表示当前弹丸的弹道倾角;γxj表示第j个离散点,即γxj=[xj,zj,vxj,vzj,θj]T;exp(·)为高斯函数。

然而预报射程前,需预先确定离散点γxj和权值Wxj。文中提取射角在一定的范围内的m条弹道曲线,并取其被动段中的弹道参数共n组(n=n1+n2+…+nm),其中每一组的弹道参数整合成γxj=[xj,zj,vxj,vzj,θj]T的形式,且将与γxj相对应的弹丸射程作为Xj。以上数据作为高维插值的离散点,所以只需确定n个权值的大小即可确定射程预报的显示方程。由式(5)～式(7)可计算出Wxj向量,得到射程预报的显示方程。而该方程仅适用于上述射角范围内的射程预估,在实际应用中,需预先将射程预报方程装入弹载计算机中,由EKF辨识后的参数作为射程预报初始点来预估。

同理,横偏预报的显示方程为:

(10)

3 仿真与分析

3.1 落点预报仿真

选取离散点的原则是基于3D质点弹道方程,采用四阶龙格-库塔法,以时间步长为0.01 s解算外弹道方程。从射角为30°～60°的范围内,每隔5°提取一条弹道,共7组。从过弹道高10 s后到落地前10 s的范围内,每隔0.1 s提取一组弹道参数,共计2 374组,记为P。按照第二章的要求将P整合成相应的数据格式,计算权值,得出落点预报的显示方程。

3.2 落点预报仿真结果分析

随机提取未录入高维插值离散点的100组弹道参数,记为Q。数据Q作为预报落点的输入,并整合成χxi=[xi,zi,vxi,vzi,θ]T和χzi=[xi,zi,vxi,vzi,θ]T的形式,落点预报仿真后得图2和图3。

由图2、图3知,射程预报的误差在0.03 m以内,而横偏预报误差在-3×10-5～4×10-5m内波动,最

大预报误差约为4×10-5m。因此,该方法预报落点的精度较好,尤其是横偏预报。同样也可以验证插值法具有对离散点及其附近点的预报精度高的特点。

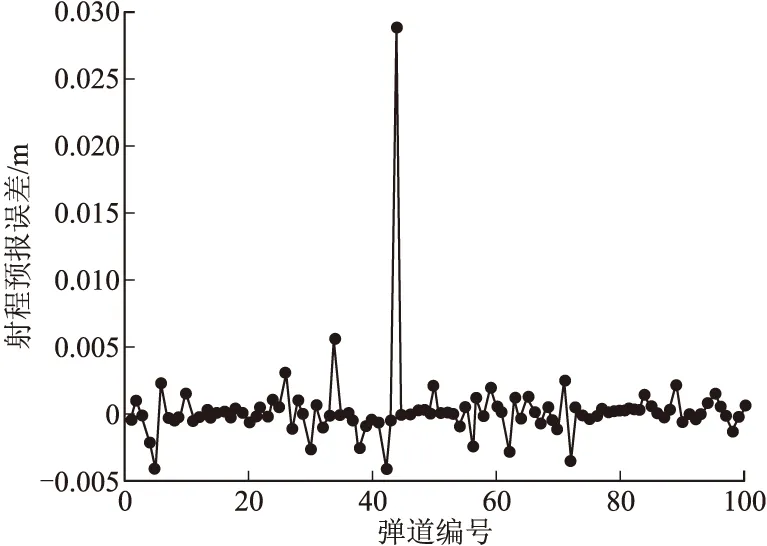
图2 高维插值法射程预报误差

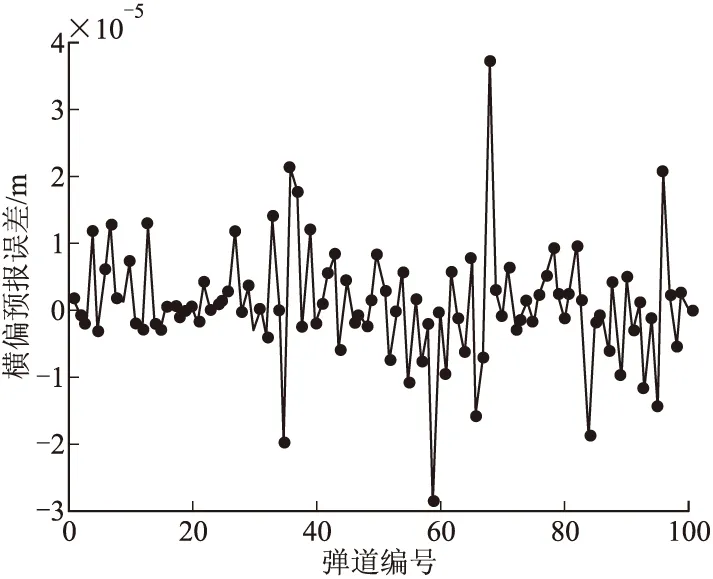
图3 高维插值法横偏预报误差

3.3 进一步验证预报精度

从射角为33°～58°范围内,每隔5°提取一条弹道曲线,共6组。并将高斯白噪声加到被动段的弹道参数中,以此作为弹载传感器采集到的弹道参数。在6条弹道曲线中,采用扩展卡尔曼滤波获得比较准确的弹道参数,分别在每条弹道中选取一组末段弹道参数作为落点预报初始点,并对高维插值法和数值积分法落点预报仿真,得到表1。

表1 高维插值法落点预报精度分析

由表1可知,高维插值法射程预报的平均相对误差为0.038 12%,而横偏预报的平均相对误差为0.106 3%,因此,该落点预报方法的精度较高,满足落点预报的精度要求。

3.4 落点预报快速性分析

高维插值法是一种以高斯函数为基底的插值方法,经插值得到落点预报方程。该方法解决了数值积分法预报落点时,由于迭代而产生的解算时间长和累积误差的不足。相比数值积分法,该方法落点预报的显示方程形式简单,更易于计算。在理论上,高维插值法落点预报的时间要少于数值积分法的预报时间。

以6条弹道为例,分别取过弹道高10 s后一点的弹道参数,将其作为高维插值法预报落点的初始值,分别采用高维插值法和数值积分法预报落点。表2为高维插值法与数值积分法预报落点的快速性分析。

表2 数值积分法与高维插值法落点预报快速性分析

由表2知,高维插值法预报射程的平均时间为1.675 ms,横偏预报的平均时间为1.831 ms,预报落点的总时间的平均值为3.506 ms,而数值积分法的落点预报的平均时间为712.902 ms。高维插值法相比于数值积分法的预报时间,平均少709.396 ms,因此,高维插值法的落点预报速度远高于数值积分法。

4 结论

文中研究了高维插值的基本原理,对末段弹道参数进行高维插值,得到落点预报的显示方程,然后落点预报仿真测试。结果表明,高维插值法预报落点的精度较高,且相比于数值积分法,在预报速度上更快。因此,可用于末修弹落点预报。但对超出离散点范围的点进行预报时,该方法预报精度不高,即泛化能力有限,这是插值法本身固有的缺陷,可通过增大选取离散点的范围或提高离散点质量等方法,降低泛化能力有限所带来的影响,提高预报精度。

[1] 赵捍东. 脉冲发动机提供控制力的火箭弹弹道修正理论及技术研究 [D]. 南京: 南京理工大学, 2008.

[2] 赵新生, 舒敬荣. 弹道解算理论与应用 [M]. 北京: 兵器工业出版社, 2006.

[3] Leonard C, Hainz III, Mark Costello. In flight projectile impact point prediction [C]∥ AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2004.

[4] 史金光, 徐明友, 王中原, 等. 卡尔曼滤波在弹道修正弹落点推算中的应用 [J]. 弹道学报, 2008, 20(3): 41-48.

[5] 戴明祥, 杨新民, 易文俊, 等. 用于卫星制导弹药落点预测的卡尔曼滤波算法 [J]. 弹箭与制导学报, 2012, 32(5): 117-120.

[6] Hainz L, Costello M. Modified linear theory for rapid trajectory prediction [J]. Journal of Guidance, Control, and Dynamics, 2012, 28(5): 1006-1014.

[7] 修观, 王良明, 杨荣军. 线性弹道模型建立与仿真 [J]. 海军工程大学学报, 2010, 22(2): 84-96.

[8] 徐明友. 高等外弹道学 [M]. 北京: 高等教育出版社, 2003.

Impact Point Prediction of Terminal Correction Projectile Based on Multidimensional Interpolation

HUANG Xin,ZHAO Handong,LI Zhipeng

(School of Mechatronics Engineering, North University of China, Taiyuan 030051, China)

In order to predict impact point of projectile fleetly and accurately, a method based on multidimensional interpolation for impact point prediction (IPP) of terminal correction projectile was put forward. Display equation of IPP was built with terminal ballistic parameters by multidimensional interpolation. Then, IPP based on multidimensional interpolation was simulated. The result shows the precision of this prediction method is higher, and the average forecast period is 3.508 ms. Compared with numerical integration for IPP, forecast period upon multidimensional interpolation is much shorter. Therefore, the method based on multidimensional interpolation for IPP is feasible.

impact point prediction; multidimensional interpolation; numerical integration; extend Kalman filter

2014-10-09

黄鑫(1989-),男,黑龙江牡丹江人,硕士研究生,研究方向:弹箭飞行与控制。

TJ013

A