一类具有饱和发生率和治疗的SEIS模型的分析
刘国永,李桂花
(中北大学 数学系,山西 太原 030051)
一类具有饱和发生率和治疗的SEIS模型的分析
刘国永,李桂花
(中北大学 数学系,山西 太原 030051)
研究了一类具有饱和发生率和治疗的SEIS模型的动力学性态.利用定义法给出模型的基本再生数,得到各类平衡点存在的条件.采用 Routh-Hurwitz 判据证明了地方病平衡点P*是局部渐近稳定的; 利用第二加性复合矩阵证明了地方病平衡点P*全局稳定性的充分条件.
饱和发生率;治疗;基本再生数;稳定性
0 引 言

关于治疗函数的研究,Wang和Ruan在文献[1]中提出在医疗资源有限时采用常数治疗率(将社区的治疗容量看作常数), 当患病者的数量很大时, 这种治疗函数是比较合理的.Wang等在文献[2]中考虑了更符合实际治疗的治疗函数h(I),
(1)
其中m=kI0,k是治疗率. 研究发现,当治疗能力较弱时, 模型会出现双稳态的平衡点, 同时也会出现后向分支.Zhang等在文献[3]中研究了具有饱和发生率及治疗函数如(1)的SIS模型的动力学性态, 发现系统发生后向分支;Li等在文献[5]中考虑了具有非线性发生率的治疗函数如(1)的SIR模型的动力学性态, 发现系统同样存在后向分支. 本文将考虑具有饱和发生率和治疗的SEIS模型, 假设潜伏期的患者不具有传染性, 染病者治愈后具有短暂免疫力, 过一段时间后又变为易感者. 将总人口(N)分为易感者(S), 潜伏者(E), 染病者(I), 考虑具有饱和发生率和治疗的SEIS模型如下:
(2)
其中正参数A表示人口的输入,d表示人口的自然死亡率,γ表示自然恢复率,μ表示因病死亡率,ε表示由潜伏者转化为患病者的概率,β是接触率系数,α为正常数并且0≤α≤1,h(I)是(1)中的治疗函数.

2 平衡点的存在性
本节将讨论系统(2)的平衡点的存在性. 很显然,系统(2)有一个无病平衡点P0(A/d,0). 若0≤I≤I0时, 令系统(2)右端为零, 有
(3)
若I0≤I时, 令系统(2)右端为零, 有
(4)
定理1 当0≤I≤I0, 也即1 下面讨论I>I0时, 系统(2)平衡点的存在性, 也即讨论方程组(4)的解的存在性. 由方程组(4)可以得到I满足如下方程: f(I)=A1I2+A2I+A3=0, (5) 其中, A1=αdεγ+[dδ+ε(d+μ)](β+αd)>0, A2=d(d+ε)(δ+k)(1-R0)+d[mβ+(mα-k)(d+ε)],A3=(d+ε)md>0. (6) 由Δ≥0, 得 (7) 或 (8) 同理, 由I2>I0, 得 (9) 综上所述,得到下面的定理: 定理2I>I0时,有 (i)系统(2)不存在正平衡点, 若满足以下条件之一: (a)R0 (ii)如果R0>p2且p4 (iii)如果R0>p2且R0>p3时, 系统(2)存在两个正平衡点P1和P2. 定理3 如果1 证明 由定理2可知, 如果R0 首先讨论无病平衡点的稳定性. 系统(2)在无病平衡点P0处的Jacobian矩阵为 特征方程为 (λ+d)[λ2+(d+ε+δ+k)λ+d(d+ε)(δ+k)(1-R0)]=0. 当且仅当R0<1时, 该特征方程的特征根均有负实部. 因此, 当R0<1时,无病平衡点P0是局部渐近稳定的; 当R0>1时, 无病平衡点P0不稳定. 定理4 如果R0<1时, 无病平衡点P0是局部渐近稳定的; 若R0>1时, 无病平衡点P0不稳定. 下面讨论正平衡点的稳定性. 当1 特征方程为 λ3+B1λ2+B2λ+B3=0. 其中 显然, 由计算机得到B1B2-B3>0成立, 根据Routh-Hurwitz判据可知, 矩阵J(P*)的特征根均具有负实部. 即地方病平衡点P*是局部渐近稳定的. 定理5 如果1 下面讨论I>I0时系统正平衡点的稳定性. 即当R0>max{p2,p3}时, 系统(2)的地方病平衡点P1和P2均存在, 但利用解析的方法很难判断其稳定性, 这里不再深入讨论其稳定性. 定理6 如果1 证明 系统(2)在P*处的Jacobian矩阵为 矩阵JP*的第二加性复合矩阵为 矩阵B = PfP-1+ PJP*[2]P-1可以写成分块矩阵 其中 (d+δ+k). 因此 所以 即有 所以满足文献[9]中定理3.3.7条件, 从而当1 本文研究了一类具有饱和发生率和治疗的SEIS模型的动力学性态. 利用定义法算出模型的基本再生数, 从而得到各类平衡点存在的阈值条件. 利用Routh-Hurwitz判据证明了地方病平衡点P*是局部渐近稳定的; 研究发现, 当1 [1]WangW,RuanS.Bifurcationsinanepidemicmodelwithconstantremovalrateoftheinfectives[J].JournalofMathematicalAnalysisandApplications, 2004, 291(2): 775-793. [2]WangW.Backwardbifurcationofanepidemicmodelwithtreatment[J].Mathematicalbiosciences, 2006, 201(1): 58-71. [3]ZhangX,LiuX.Backwardbifurcationofanepidemicmodelwithsaturatedtreatmentfunction[J].Journalofmathematicalanalysisandapplications, 2008, 348(1): 433-443. [4]HuZ,LiuS,WangH.Backwardbifurcationofanepidemicmodelwithstandardincidencerateandtreatmentrate[J].NonlinearAnalysis:RealWorldApplications, 2008, 9(5): 2302-2312. [5]LiXZ,LiWS,GhoshM.StabilityandbifurcationofanSIRepidemicmodelwithnonlinearincidenceandtreatment[J].AppliedMathematicsandComputation, 2009, 210(1): 141-150. [6]HadelerKP,VandenDriesscheP.Backwardbifurcationinepidemiccontrol[J].MathematicalBiosciences, 1997, 146(1): 15-35. [7]ArinoJ,McCluskeyCC,vandenDriesscheP.Globalresultsforanepidemicmodelwithvaccinationthatexhibitsbackwardbifurcation[J].SIAMJournalonAppliedMathematics,2003, 64(1): 260-276. [8]DushoffJ,HuangW,Castillo-ChavezC.Backwardsbifurcationsandcatastropheinsimplemodelsoffataldiseases[J].Journalofmathematicalbiology, 1998, 36(3): 227-248. [9] 马知恩, 周义仓, 王稳地, 等. 传染病动力学的数学建模与研究[M]. 北京:科学出版社,2004. [责任编辑:王军] ·学术动态· 华东师范大学博士生导师何品刚教授莅临我校讲学 2015年4月27日上午,应我校化学化工学院的邀请,华东师范大学化学系博士生导师何品刚教授在文化路校区化学实验楼311室作了题为“DNA电化学生物传感技术研究”的学术报告.报告会由化学化工学院院长赵文献主持,化学化工学院部分师生聆听了报告. 何品刚教授首先从传统DNA电化学传感器、纳米材料修饰电极的DNA电化学传感器和均相非固定体系DNA传感器三个方面介绍了他的课题组开展相关科研工作的研究背景.随后,何品刚教授介绍了他的课题组在利用电子扫描电镜进行多通道基因突变的检测、基于荧光on-off原理实现电化学的基因检测以及合成多种联吡啶钌功能化的环糊精分子用于DNA及其他生物分子检测分析方向的最新研究成果,并与化学化工学院的教师们进行了深入的学术交流. 何品刚教授语言朴实幽默、逻辑清晰,研究背景贴近生活,研究内容新颖前沿.本场精彩的学术报告让大家受益匪浅,博得了全体与会师生的阵阵掌声,尤其何教授的课题组在多通道基因突变分析方面的创新性研究工作博得了在场师生的一致赞许.会后,何教授与我校生物分子识别与传感河南省高校重点实验室的科研人员就研究生培养及专业方向的一些学术问题进行了讨论和交流. 何品刚,博士,教授,华东师范大学博士生导师,任上海化学化工学会分析化学专业委员会主任,上海市欧美同学会常务理事,华东师大分会会长.主持科技部863重点项目“重大环境污染事件特征污染物现场快速检测技术系统”课题;国家自然科学基金项目“电致化学发光DNA探针”、“基于有序纳米电极材料和纳米标识剂构建新型纳米生物传感器的研究”、“基于新型联吡啶钌环糊精衍生物和主-客体识别的电致化学发光生物传感技术研究”和“均相DNA杂交电化学生物分子识别技术的研究”等课题.在J.Am.Chem.Soc,Chem.Comm.,Anal.Chem.等SCI杂志上发表研究论文160余篇. Analysis of an SEIS epidemic model with saturated rate and treatment LIU Guoyong, LI Guihua (Department of Mathematics, North University of China, Taiyuan 030051,China) The dynamical behaviors of an SEIS model with saturated rate and treatment is investigated. The basic reproduction number of the model is given by using the definition,and the existing threshold conditions of all kinds of the equilibrium points are obtained. Locally asymptotic stability of the endemic equilibriumP*isprovedbyusingtheRouth-Hurwitzcriterion,andthesufficientconditionsofglobalasymptoticstabilityoftheendemicequilibriumP*isalsoobtainedbyusingthesecondadditivecompoundmatrix. saturated rate; treatment; basic reproduction number; stability 2015-01-15 国家自然科学基金资助项目(11201434) 刘国永(1989-),男,山西塑州人,中北大学硕士研究生,主要从事应用数学的研究. O A文献标识码:1672-3600(2015)06-0010-06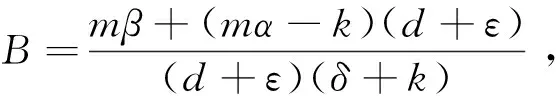


2 平衡点的局部稳定性

3 平衡点的全局稳定性



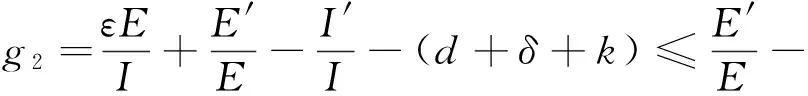

4 总 结

