基于SIR模型对埃博拉病毒感染人数增长率的确定
刘雅倩,刘元志,朱家明,章启明
(1.安徽财经大学 金融学院,安徽 蚌埠233030;2.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030;3.安徽财经大学 经济学院;安徽 蚌埠 233030)
基于SIR模型对埃博拉病毒感染人数增长率的确定
刘雅倩1,刘元志3,朱家明2,章启明3
(1.安徽财经大学 金融学院,安徽 蚌埠233030;2.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030;3.安徽财经大学 经济学院;安徽 蚌埠 233030)
针对埃博拉病毒感染人数增长率确定的问题,建立SIR改进模型,结合历史数据,定量预测出未来感染人数增长率值,结合所建立的SIR改进模型,分析出当接触率为大于死亡率时,应该研发新的药品,药品的生产计划要满足药品的需求,通过分析不同阶段的药物需求,制定未来3年各生产地的生产计划.
埃博拉;SIR传染病模型;药品生产计划
2014年2月埃博拉[1]开始爆发于西非,截至2014年10月31日,世界卫生组织关于埃博拉疫情报告称,几内亚、利比里亚、塞拉利昂、美国、西班牙、马里以及已结束疫情的尼日利亚与塞内加尔累计出现埃博拉确诊、疑似和可能感染病例13567例,其中4951人死亡.同时,埃博拉病毒的爆发也带来了民航禁飞、人力损失、经济受创、粮食短缺等多方面的影响.如何有效地抗击埃博拉病毒已经成为全世界关注的热点,然而,如果能够掌握埃博拉病毒的发病特征并及时地研发出药品,则会很好地控制埃博拉病情的蔓延.本文就是基于SIR传染病模型,针对西非三国(几内亚、利比里亚与塞拉利昂),思考如何预测埃博拉病毒感染人数的增长率与确定药品生产计划,从而迅速有效地控制埃博拉病毒蔓延(相关数据见2014年第三届“认证杯”数学中国数学建模国际赛试题C题[2]).
1 埃博拉病毒感染人数增长率的预测
1.1 研究思路
由于目前生产的药品只能治愈早期病人,所以根据现实情况,我们对病人身体状况进行进一步划分,将病人分为早期病人与晚期病人,早期病人可以治愈,晚期病人只有面临死亡.早期病人病愈之后成为治愈病人,查阅资料可知,当埃博拉病人接受治疗之后,对病毒存在免疫能力,不会再患病,所以患病病愈之后的健康者视为系统中的移出者.同时,那些晚期病人由于无法治愈成为死亡人,也将移除系统.根据不同人群的身体状况,我们将人群健康状况划分为以下5种:没有免疫能力的健康人,有免疫能力的健康人,早期病人,晚期病人与死亡人,并将这5种状态之间的转移情况表示为如下图形.
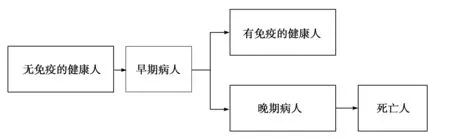
图1 5种身体状况状态转移图
假定总人数N不变,将人群划分为5类,即健康者、早期病人、晚期病人、死亡病人移出者与治愈病人移出者,时刻t5类人在总人数中的占比记为s(t),e(t),l(t),d(t)和r(t);
假设病人的接触率为λ,死亡率为μ,β为早期病人到晚期病人的人数比率,α为早期病人治愈率(因为根据题意,我们假设只有早期病人可以治愈,晚期病人只有死亡).
可以得知s(t)+e(t)+l(t)+r(t)+c(t)=1,同时,对于死亡病人移出者而言应有:
再记初始时刻的健康者和病人的比例分别为s0(s0>0)和i0(i0>0),则可以表达出如下的方程:
1.2 参数值的确定
要对这个模型进行求解,必须能够先得到这个模型中的未知参数的值[3].我们要知道的确定值得未知参数有:接触率为λ,死亡率为μ,β为早期病人到晚期病人的人数比率,α为早期病人治愈率.其中μ,β和α都可以通过查阅资料的方式得到一个估计值.
λ值是最难确定的,而λ值是取决于一个地区的卫生医疗水平.在当我们设定一个地区或者国家时,其卫生医疗水平在短时间内不会变动,那么λ值也会相应固定下来.这里我们使用最简单的传染病模型——SIR模型[4]对λ进行估值,由于使用数据一样,都是相同国家或地区在相同时间的人口总数,病人累计数与死亡累计人数,所以通过SIR模型计算出来的λ值能相对近似拟合出模型中的λ值.
1.2.1λ值的确定——SIR模型
假定总人数N是定值,将人群划分为三类,即健康者、病人、死亡病人的移出者,时刻t三类人在总人数中的占比记作s(t),i(t)和r(t),可以得到如下方程.
首先以几内亚对于建立的模型,设定μ=0.012524954,s0=0.999995625,i0=0.000004375.在这个模型中只有λ为参变量,不断对λ值进行调试,使得预测模型的曲线变动情况尽可能地拟合出真实情况,得出最优的拟合情况如下.
从图2可以看出从250d开始,拟合曲线与真实值曲线出现明显偏差,出现这样偏差的原因可能是:在前期埃博拉病毒爆发时,社会各个部门还没有时间做出有效措施,在后期,社会各部门的一些保护防范措施起到一定的作用,从而使埃博拉病毒的感染速率有所降低.所以这里以第250d为分割点,以第1~250d作为第一阶段,250~311d作为第二阶段,对图形进行分段拟合,第一阶段拟合情况较好,见图3,对第二阶段重新拟合,拟合结果如下图.
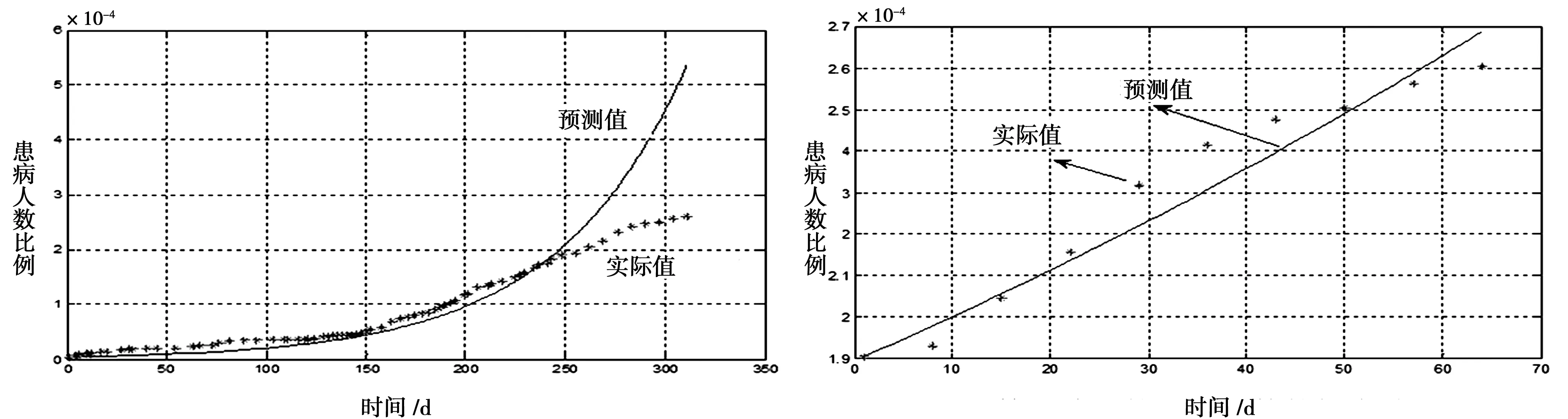
图2 病人比例的拟合结果 图3 第二阶段的患病人数的拟合结果
计算出250d之前的λ=0.028,250~311d,λ=0.018.由于λ值是由当地医疗卫生水平决定的,并且为了真实拟合出现阶段的λ,所以选取以离现阶段时间最近的λ作为预测值,则使用λ=0.018.
同理,得到利比里亚与塞拉利昂两个阶段的λ值,并将计算出的λ值与查阅文献获得的值进行对比,可以看出计算结果相对比较合理正确.

表1 计算出λ值与查阅文献获得λ值的对比
1.3 参数值的确定
根据前面的分析,我们可以确定μ,β,基于这个方程,对早期病人与晚期病人的人数分别进行求解,发现当早期病人治愈率α与接触率λ不相等时,我们得到图4和图5,其中绿色的曲线表示的是晚期病人所占比率变动情况,蓝色曲线表示的是早期病人所占比率的变动情况,可以看出随着药物的使用,晚期病人人数先快速上升最后慢慢下降直至趋于零,早期病人人数会一直下降直至趋于零;当早期病人治愈率α与接触率λ相等时,我们得到图5,可以看出随着药物的使用,晚期病人人数先快速上升最后维持在一个水平,早期病人人数会一直下降直至维持于一个水平.

图4 第一种晚期病人与早期病人人数变动情况 图5 第二种晚期病人与早期病人人数变动情况
2 药品生产计划的确定
2.1 是否研发药品
首先,疾病本身的特性是决定是否需要生产新药品的关键.如果一种疾病是具有显著周期性或者说,这个疾病不会根本消失,那么就有必要准备生产药品以防备疾病随时来袭.
其次,根据研究一所建立的模型可以分析出σ=1是一个阈值,因为当σ>1时,i(t)的增减性取决于i0的大小,但是其极限值随着σ的增加而增加,当σ≤1时,病人比例i(t)越来越小,最终趋近于0,这是由于传染期内经有效解除从而使健康者变成的病人数不超过原来病人数的缘故.所以当σ>1时,即为当3d累计接触率为λ大于3d累计死亡率ω,应该研发新的药品.
2.2 药品生产计划的确定
根据一般药物的规模化生产进程,假设该药物在半年后可以达到较大的生产能力,可以满足同时期的药物需求量,其生产能力的增长是线性的.
结合一般疫苗的保质期,同时考虑节约成本,药物3个月进行一次运输,但其中第一个月刚开始生产药品时应及时运输.即第一个月为周期一,此后周期长度都是3个月.
因为该药物只能治愈早期病人,因此以早期病人数量为研究对象,作为药物需求的依据,从而制定生产计划.为平衡生产压力,每个产地生产相同数量的药物.
2.2.1 模型的建立
药品的生产计划要满足药品的需求,通过分析不同阶段的药物需求,制定未来3年5个生产国的生产计划[5].
⑴第一年
生产能力需要经历逐步增长的过程,在初期没有大规模生产的能力,因此,第一年投放药物的目的是控制埃博拉疫情,使其不爆发.第一年的第一个月,即生产计划的第1期,新药物初步进行生产,没有药物投放到灾区,灾区疫情按照目前形势发展,第1期生产的药物用来满足灾区第2期的需求,则有:

其中,i为生产计划的期数,Di为第i期的药物需求量,k表示生产初期药物生产力随时间增长的能力,t为时间(d),ei为第i期的早期病人比例,P为非洲3国总人口,α1是治愈所有患病人的治愈率,α2是使埃博拉疫情不至于爆发时的治愈率.
同理,对于生产计划的第二期:

其中x表示,在第二期结束前x天,可以停止生产扩张,此时的生产能力已经可以满足需求.
半年后,从第三期开始,生产能力已经足够满足需求,此时药物的供需平衡满足:

⑵第二年
生产力经过第一年发展,已经可以满足非洲三国的需求,第二年的目的是提供足够的药物,治疗所有患病者,此时:

⑶第三年
第三年的目的是在治疗所有患病者,为健康人提供疫苗,彻底根除埃博拉病毒.提供疫苗的数量与当时的患病人数成正比,我们合理假设所有与病人接触过的人都要接种疫苗,则此比例应该等于本文改进SIR模型中的接触率,此时:

2.2.2 模型的解决
首先,根据研究一所建立的SIR改进模型,通过MATLAB编程求解,得到在此药物供给计划下,非洲3国未来3年12期的早期病人数量之和.
如图6,第一年前期期埃博拉仍在以较快速度传播,是因为刚研制出药物,还没有投入使用;第一年后期埃博拉病毒得到抑制,是因为药物投入使用,使早期病人数量逐渐减少并趋于稳定,第二年、第三年均能向灾区供给充足的药物,因此早期病人数量逐渐减少直至趋近于0.
根据前面建立的公式,结合未来3年早期病人预测值,生产力发展时线性增长;生产力充足,每天生产的药物数量刚好满足每天需求.此时,可以用生产地每天的产量表示每日实际发挥的生产力的变化.

图6 药物供给计划下的早期病人预测 图7 每天运输药物时实际发挥的生产力(所有产地生产量之和)
由于实际生活中不是每天都要运输药物,而是按周期运输,因此在每一期的生产中采用平均速度生产即可,可以得到每个生产地的生产计划.

表2 每个生产地每期面临的总需求和生产速度(剂量/d)
3 总 结
以西非3国(几内亚、利比里亚与塞拉利昂)作为分析对象,建立SIR改进模型,对埃博拉病毒感染人数增长率进行预测.基于建立的SIR改进模型,分析出当接触率大于死亡率,应该研发新的药品,并预测出每一期的生产中每个生产地的生产计划.本文将SIR模型与现实意义结合,对进一步对抗埃博拉病毒蔓延有一定的参考价值.
[1] 刘安立.埃博拉全解读[J].大自然探索,2014(10):8-21.
[2] 第三届数学中国数学建模国际赛:http://mcm.tzmcm.cn/[EB/OL].2014-12-01
[3] 何艳辉,唐三一.经典SIR模型辨识和参数估计问题[J].应用数学和力学,2013(03):2-4
[4] 刘冠军.SIR传染病模型的辨识分析及稳定性分析[D].信阳:信阳师范学院硕士学位论文,2011.
[5] 王汉斌,于军生.基于关键链理论的多项目生产计划制订与控制模型构建[J].中国高新技术企业,2010(06):55-57.
[责任编辑:王军]
Determination on the infections growth rate of the Ebola virus based on the SIR model
LIU Yaqian1, LIU Yuanzhi3,ZHU Jiaming2, ZHANG Qiming3,
(1.School of Finance Anhui University of Finance and Economics;2.School of Statistics and Appl. Math;3. School of Economic,Bengbu 233030,China)
As for determining the infections growth rate of the Ebola virus, we establish SIR improvement model. We predict the growth rate value of infecting since the outbreak of Ebola after our quantitative analysis. Using the established SIR improved model, we come to the conclusion that when the contact rate is greater than the death rate, it is time to develop a new drug. At the same time, after analyzing the drugs demand in different stage, we predict the deadline for research and development and the production of drugs.
Ebola; SIR epidemic model; drug research and development
2014-11-06
国家自然科学基金资助项目(11301001);安徽财经大学教研项目(acjyzd201429)
朱家明(1973-),男,安徽泗县人,安徽财经大学副教授,硕士,安徽财经大学数学建模实验室主任,主要从事应用数学与数学建模的研究.
R373.32
A
1672-3600(2015)06-0025-05

