基于超立方体Qn节点编码的边不交最优路径
陈荷花
(太原学院, 山西 太原 030012)
基于超立方体Qn节点编码的边不交最优路径
陈荷花
(太原学院, 山西 太原 030012)
基于超立方体节点编码的特点,得到了n维超立方体Qn中任意两节点s、t之间的两条并行最优路径算法.该算法共包括了11步骤,在最坏的情况下需要执行2n2+4n2次运算,它的时间计算复杂度为O(n2),属于多项式算法.
超立方体;节点编码;边不交;最优路径
0 引言
寻找关键路径、设计路由算法是互连网络中实现源节点和目标节点之间进行通信的关键技术,它的优劣直接影响着并行计算机的处理性能.目前求解最短路径所使用的最基本、最广泛的算法,是由F W Dijkstra提出的Dijkstra算法[1],许多文献也讨论过该算法的实现方法,具体网络结构中也提出过各种改进方法[2-3],但作为最短路径问题的关键环节,其计算过程过于复杂,数据存储过于庞大.
超立方体互连网络独具的对称性、正则性、可扩展性等性质,一直以来深受学者们的偏爱.2014年,陈荷花、高太平在该网络上提出了实现源节点和目标节点之间通信的一条最短路径[4],并利用实例验证了算法的高效性.同一年,Cheng-Nan Lai在n维折叠超立方体上给出了one-to-mang点不交的最优路径算法[5],进一步分析得到其算法复杂度为O(n3).
2011年,张丽果、杜慧敏、韩俊刚研究了一种超立方体变形网络结构——Mobius立方体,给出了这个网络上一种新的最短路径路由算法[6],避免了递归调用,还指出了算法的时间复杂度为O(n).
1 预备知识

文中未定义的记号和术语,请参见文献[7].
定义1 若Qn中节点s、t有h个不相同的编码分量,则称节点s、t有h个不同位.显知节点s、t有n-h个相同位.
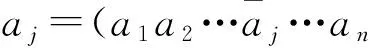
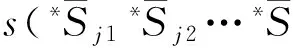

在n维超立方体Qn中,两节点s、t相邻,当且仅当dH(s,t)=1.
定义5 超立方体Qn中一条以s为始点,t为终点,途径节点v1,v2,L,vk的路径记作P(s,t)=sv1v2…vkt,也可简记为P=sv1v2…vkt.
2 边不交的最优路径算法
2.1 算法的思想
首先,确定超立方体Qn中始点s和终点t,计算出它们之间的汉明距离,记为dH(s,t)=h,这时,我们便得知节点s、t之间存在着h个不同位.
然后从两个方向开始寻找所求路径.一是改h个不同位中的最高位为其互补位,得所求路径上继始点s后的第一个节点v1,再改h个不同位中的次高位为其互补位,得所求路径上继节点v1后的又一个节点v2,……,依次下去,可得到超立方体Qn中从始点s到达终点t的一条最优路径P1=sv1v2…vh-1t;二是改h个不同分量中的最低位为其互补位,得所求路径上继始点s后的第一个节点u1,再改h个不同位中的次低位为其互补位,得所求路径上继节点u1后的又一个节点u2,……,依次下去,可得到超立方体Qn中从始点s到达终点t的另一条最优路径P2=su1u2…uh-1t.
特殊情况——Qn中始点s和终点t相邻.
1)当n=2时,显然它们的连线就是一条最优路径,而另一条最优路径是P=suvt,dH(s,t)=3.(如图1所示).
2)当n≥3时,其中一条最优路径是节点s、t的连线,另一条可能是P=suvt,还有可能是Psu1v1t=(如图2所示).此时,依然有dH(s,t)=3.(说明:依据超立方体的对称性、可扩展性知图2总能在Qn中找到).

图1 2维超立方体Q2

图2 3维超立方体Q3
2.2 算法步骤
求解n维超立方体Qn中任意两节点s、t之间的两条并行最优路径算法的具体步骤如下:
算法输入:始点s=(s1s2…sn),终点t=(t1t2…tn),置i=1,k=1.
①计算汉明距离dH(s,t)=h.
②取始点s和终点t编码分量中的第i位si,ti.
③若si=ti,置i=:i+1,转②;否则,进入下一步.
④记i=jk,Si=Sjk.
⑤若i ⑥记录Sk=S(*Sj1*Sj2*…Sjk*). ⑦若k ⑩若w 2.3 算法的框图 这里给出该算法的流程图如图3所示. 2.4 算法的复杂度分析 例在四维超立方体Q4中,求出从节点(1110)到节点(1001)的两条并行最优路径.(如图4所示) 图3 两条边不交最优路径算法流程图 首先输入始点s=(1110),终点t=(1001). 计算s、t之间的汉明距离dH(s,t)=3. 对比s、t各编码分量,记录Sj1=1,Sj2=1,Sj3=0, v1=(1010),v2=(1000),v3=(1001)=t, u1=(1111),u2=(1101),u3=(1001)=t, 得所求并行最优路径 P1=(1110)(1111)(1101)(1001),P2=(1110)(1111)(1101)(1001). 本文基于超立方体的节点编码特点,给出了n维超立方体Qn中任意两节点s、t之间的并行最优路径算法,并利用实例验证了该算法的正确性和有效性,为设计超立方体互连网络中并行单播路由算法提供了强有力的理论支撑.论文下一步的工作将考虑,在限制该网络中的某些节点的情况下,如何找到源节点和目标节点之间的最优路径. [1] Wang zhihe,Ling Yun.The Optimization and Implementation of the Shortest Path Dijkstra Algorithm[J].Microcomputer Information,2007,23(33):275-277 [2] 李彦平,魏 昆,王 丹.基于极小代数赋权有向图最短路径求解算法[J].沈阳大学学报(自然科学版),2015,27(1):25-29 [3] 王树西,吴政学.改进的Dijkstra最短路径算法及其应用研究[J].计算机科学,2012,39(5):223-228 [4] 陈荷花,高太平.基于超立方体Qn节点编码的最短路径[J].宜宾学院学报(自然科学版),2014,14(6):92-93 [5] Cheng-Nan Lai.An efficient construction of one-to-mang node-disjoint paths in folded hypercubes[J].J.Parallel Distrib.Comput,2014,74:2310-2316 [6] 张丽果,杜慧敏,韩俊刚.基于Mobius立方体的最短路径路由算法[J].系统工程与电子技术,2011,33(12):2743-2748 [7] 徐俊明.图论及其应用[M].合肥:中国科学技术大学出版社,2004 Edge-disjoint Optimal Paths in Hypercube QnBased on Node Codes Chen Hehua (Taiyuan University,Taiyuan 030012, China) Based on the characteristic of the node codes in the n-dimensional hypercube,theauthor of this paper got an efficient algorithm for two edge-disjoint optimal paths between anytwo nodes.This algorithm involves eleven steps.In the worst case you need to execution2n2+4n2times calculation.Its algorithm complexity is O(n2),so it belongs to a polynomialalgorithm. hypercube; node code; edge-disjoint; optimal path 2015-01-28 陈荷花(1983-),女,山西长治人,硕士,太原学院讲师,主要从事图论研究. 1672-2027(2015)02-0024-04 O242 A
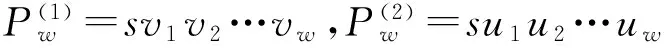

3 算法实例验证

4 结束语

