基于QPSO-RBF神经网络的交通流量预测方法

王 惟

(晋中学院 数学学院,山西 晋中 030600)

基于QPSO-RBF神经网络的交通流量预测方法

王 惟

(晋中学院 数学学院,山西 晋中 030600)

提出一种粒子群优化神经网络的预测方法,首先基于改进的量子行为粒子群算法对神经网络进行训练,以保证各权值和阈值能得到最优解,同时对训练样本进行了基于聚类算法的优选．最后进行了仿真验证,证明本文方法用于短时交通流量预测可以获得较高的精度并且误差稳定,为交通流量预测的实际应用提供了一种参考．

RBF神经网络;量子行为粒子群算法;交通流量;预测

0 引言

我国的城市交通拥堵已经成为了城市生活面临的主要问题之一,交通拥堵导致了严重的能源浪费和环境污染,对生产和生活均带来了不利影响．准确及时的预测交通流量的变化,可以为提前疏导和分流提供技术支持,是高效利用道路网络,实现城市智能交通的基础[1]．

然而实际上,影响交通变化的因素众多,如上游路段交通状况[1]、时间因素、当前交通状况等,且各因素对结果的作用过程复杂,属于典型的复杂非线性时变系统．由于各影响因素与结果之间的具体关系没有显式表达式或高精度的逼近表达式,这就给使用传统数学方法预测交通流量带来了很大困难．因此诸多学者求诸人工智能方法,如时间序列分析法[2],神经网络法[3-7],支持向量机方法[8],等．其中神经网络方法因具有良好的学习能力和容错能力而得到了广泛的应用[3,4],并取得了良好的效果．在众多的神经网络类型中,RBF网络的逼近能力尤为突出[4,9,10],为此本文即采用一种改进型的RBF网络进行交通流量的预测．

RBF神经网络作为一种典型的有导师学习网络,其输入与输出之间的映射性能取决于训练样本和训练方法,而映射性能的优劣又决定了其预测精度的高低．为此,文献[3,5,8]采用了基于灰色理论的改进方法,文献[4,11]采用了粒子群的方法进行神经网络的训练,均取得了较好的效果．本文则应用了寻优搜索性能更好的量子行为粒子群优化算法(记为QPSO)进行网络的训练,同时,基于聚类分析原理对训练样本的构成进行了优化．

1 基于RBF神经网络的交通量预测

一般情况下,影响交通流量的因素有之前时段和当前时段交通状况,上游交通状况,不同时间点的影响,等．那么可以认为存在这样的关系:

(1)

在式(1)中,Xt=(Vt,Ut,t),Vt=(v1,v2,…,vn)表示本路段上游n个路口的交通流量,Ut=(ut-1,ut-2,…,ut-m)表示本路段之前m个时间段内的交通流量,t表示当前时刻,X称为输入向量,yt表示对应的t时刻的交通流量,称为输出向量．如果求得映射关系F(·),就预测下一时刻的交通流量值yt了．显然,映射关系F(·)为一复杂的高维函数,一般的初等表达式难以准确描述这种关系．为了解决这一问题,本文使用RBF神经网络,实现对(1)式的高精度逼近:

(2)

其中Γ(·)在表示输入量与输出量之间的映射关系．RBF神经网络的结构如图1所示[10]:

图1 RBF神经网络结构

令(Vt,Ut,t,yt)表示由各影响因素与对应的交通流量信息构成的欧氏空间中的点,那么当这些点的数量足够大时,即可实现对F(·)的高精度插值逼近．RBF神经网络是基于高维插值理论而构造的,当结构、激励函、权值、阈值等合理时,就可以实现Γ的功能[12]．

经典的RBF训练一般通过聚类算法完成,经聚类后的一组子样本就构成一个神经元．对网络进行合理的训练后,网络中形成的映射关系可以用数学的方式表达为:

(3)

其中:

(4)

2 训练算法的改进

2.1 基于粒子群优化的训练方法

在利用粒子群优化算法训练神经网络的工程中应用中,每一个粒子都是一个可能的解向量,粒子个体通过以下规则进化搜索,实现寻优[12-14]:

(5)

在上式(5)中的符合意义与文献[12-14]一致．

那么这些粒子也就是待求的经元数量、权值、阈值构成的一个向量,起始位置就是这一向量的初始值．即:

(6)

通过搜索寻优得到的粒子的最优“位置”也就是所求的能使神经网络的性能最优的神经元数、权值和阈值．

粒子群优化因其特定的进化算法和搜索过程,存在着诸如早熟、不能保证搜索整个可行解空间等问题．所以本文中改进后的量子行为粒子群算法实现神经网络的整体优化．QPSO的解算框架更简单,协同能力也得到了很大提高,这就增强了搜索全局最优解的能力[13,14]．QPSO典型改进之处在于引入了势点(p点)的概念[13],用以表示每个进化中的粒子都可能会随机收敛于某一点,这也是AQPSO算法对量子思想的体现．对于势点的数学描述为:

(7)

同时定义:

(8)

(9)

(10)

式中pi,j是单个粒子的当前最优位置,而pg则通过式(8)求解,式(8)中的a是在0与1之间的一个随机数,式(9)中的f(·)称之为适应度函数,用以衡量粒子进化的效果,在本文中设定f(·)为下式中的函数,用以描述当前的权值和阈值下被训练的神经网络的理论输出与实际输出的符合程度:

(11)

(12)

(13)

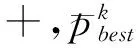
(14)

同时将式(13)改进为:

(15)

2.2 基于因子分析的样本优选

所谓聚类分析就是指根据被研究对象的某些特征,把相似性较高的个体归为一类,也可以认为是一个子集[16,17]．一般的聚类算法是一种称之为“硬划分”的规划方法,但这并不适合每一种具体的情况,像神经网络的训练样本这种数据,其间没有明确的隶属关系,此时就需要对聚类进行相对模糊的定义,也就更适合软划分方法．为此本文使用了一种广泛应用的软划分方法,即模糊聚类方法,用以对训练样本进行优选．具体的操作过程,便是基于FCM的方法对神经网络的训练样进行聚类处理[16],所谓FCM算法可以转化为特定的数学规划问题,其原理为:

(16)

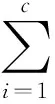
(17)

(18)

这里c表示聚类的类别数．那么聚类过程可以表述为:

步骤1:选择合适的聚类数的范围[cmin,cmax];

步骤2:对于c∈[cmin,cmax]:

1)初始化聚类中心V;

2)使用FCM算法更新参数U,V;

3)判断算法的收敛性,如果不收敛,则转回(2),如果收敛,则转步骤(4);

4)计算指标函数值V(c);

步骤3:比较各指标函数值V(c),最大的指标函数值V(ci)里的ci就是所求的最佳聚类数;

将样本进行基于聚类的优化,是为了避免某一类型的样本的过分集中而导致神经网络的权阈值偏离最优解,毕竟神经网络的训练是从样本中寻找规律,所以样本选取的合理与否就在很大程度上决定了训练的效果,聚类之后需要人为删除一些过于集中的训练数据,使数据更均匀的分布在整个空间上．

3 仿真与分析

3.1 训练与预测

选取晋中市某路段的交通数据进行预测试验,统计6天的车流量数据,从早上7点钟开始到晚上6点,将每隔10分钟的交通状况选取一次样本．将周一至周五的数据编制为训练样本,以第二周周一的数据进行测试．作为有导师学习的神经网络,其预测精度一方面取决于训练方法,另一方面取决于训练样本是否能真实反映系统特性．为了使样本分布均匀并且更具有“代表性”,根据式(1)中的量编制样本后,基于上文中的模糊聚类的方法优化训练样本,以提高训练效率见图2．

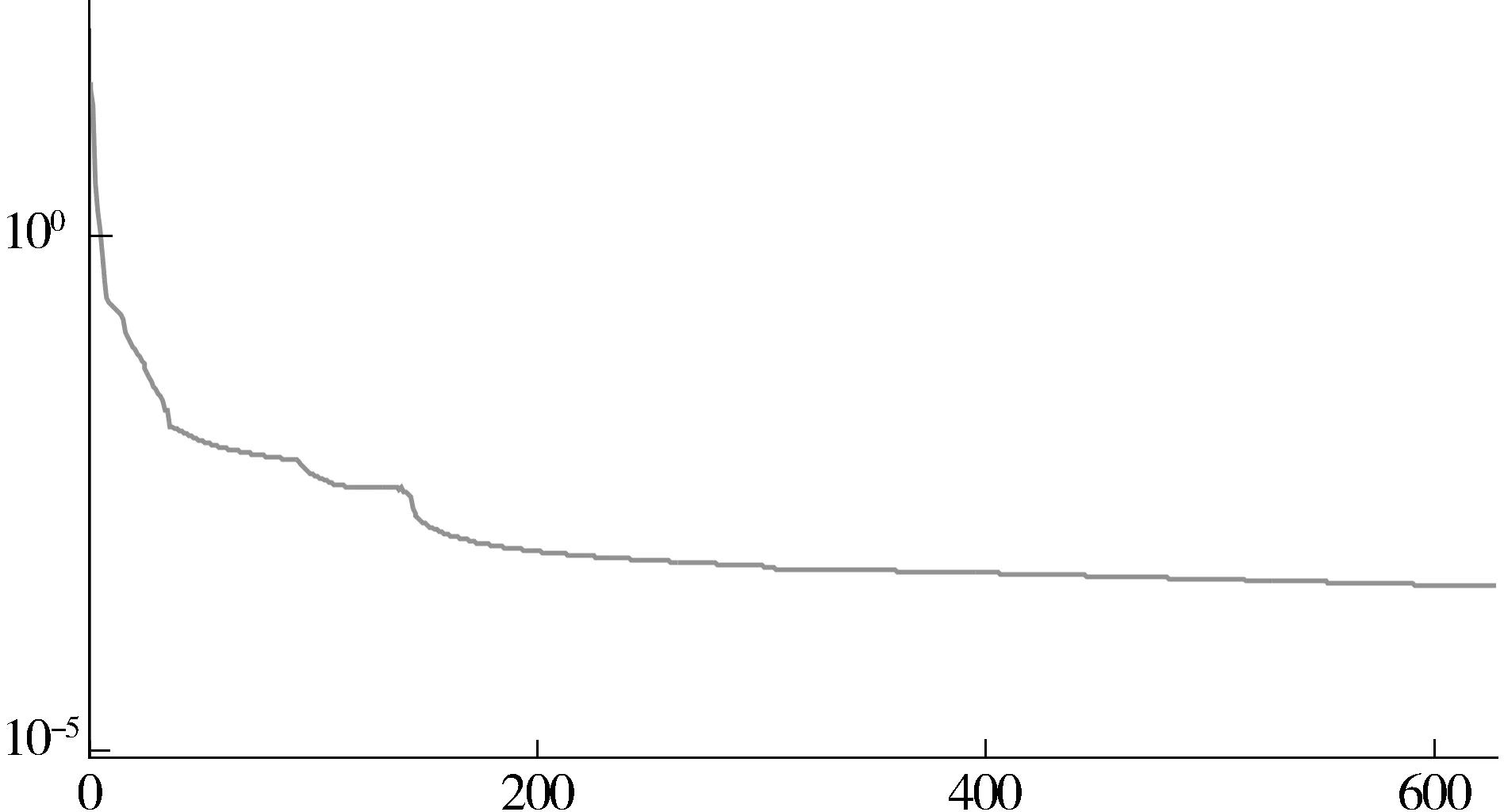
图2 训练效果

从图2中可以直观的看出,基于优选样本和优化学习的训练方法误差下降速度快并趋于稳定．训练完成后进行测试．交通流量的预测效果如图3、4所示．

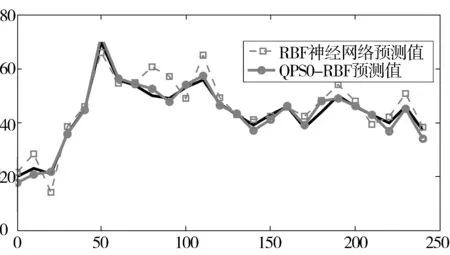
图3 交通流量预测效果

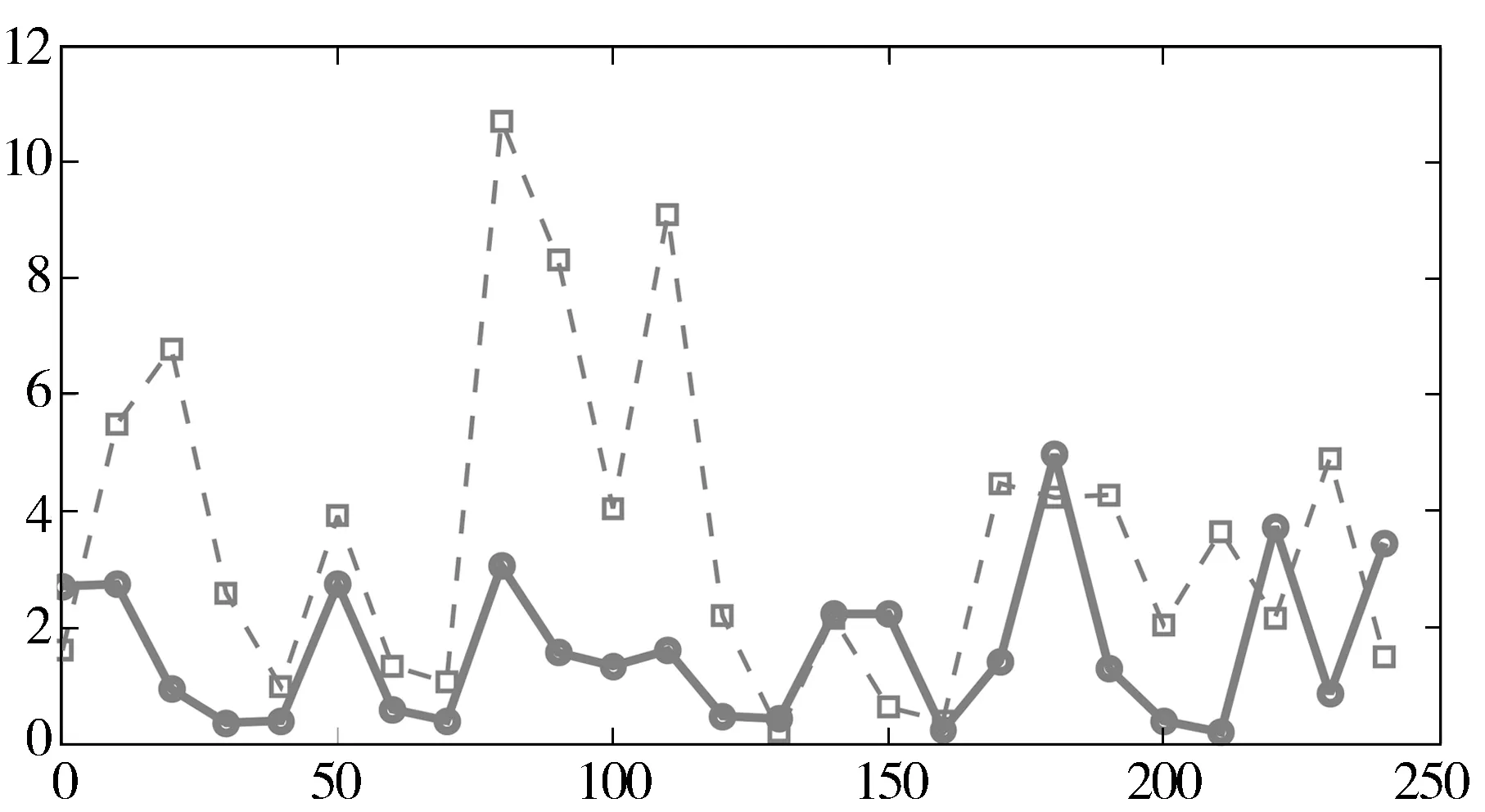
图4 预测误差统计

3.2 数据分析

从图3可以看出,本文提出的优化训练样本和训练过程的方法,预测精度较高,并高于普通RBF神经网络方法．由于模型误差和随机误差的存在,预测值和实际值之间仍有一定的偏差,这一方面是由于单日的交通流量受一些不可知因素的影响,且具有一定的随机性,另一方面就是由于神经网络的模型和输入神经元的选取,还无法达到最优．考虑外界的随机扰动和时间相关性,在神经网络方法中引入时间序列分析法[2],是今后有望进一步提高预测精度的途径之一,也是今后工作的一个方向．

4 结语

本文使用了RBF神经网络进行交通流量的预测,并对训练样本做了基于模糊聚类的优选,对训练算法做了基于自适应量子行为粒子群算法的改进．最后进行了预测测试,说明:

1)基于RBF神经网络的方法用以预测交通流量具有较好的精度,对实际工程应用有一定的借鉴意义;

2)本文使用的样本优选法和训练优化法可以在一定程度上提高预测精度．

[1] Yubin Wan,Jan H.van Schuppen,Jos Vrancken.On-line distributed prediction of traffic flow in a large-scale road, network[J].Simulation Modelling Practice and Theory,2014,47(1):276-303

[2] 吴建军,徐尚义,孙会君.混合交通流时间序列的去趋势波动分析[J].物理学报,2011,60(1):1-7

[3] 陈淑燕,王 炜.交通量的灰色神经网络预测方法[J].东南大学学报(自然科学版),2004,34(4):541-544

[4] 崔吉峰,乞建勋,杨尚东.基于粒子群改进BP神经网络的组合预测模型及其应用[J].中南大学学报(自然科学版),2009,40(1):190-194

[5] 张敬磊,王晓原.交通流灰色RBF网络非线性组合预测方法[J].数学的实践与认识,2011,41(19):1-7

[6] Kranti Kumar,M.Parida,V.K.Katiyar.Short term traffic flow prediction for a non urban highway using Artificial Neural Network[J].Procedia-Social and Behavioral Sciences,2013,104:755-764

[7] LI Rui,CHEN Jian-ya,LIU Yun-jie,et al.WPANFIS:combine fuzzy neural network with multiresolution for network traffic prediction[J].The Journal of China Universities of Posts and Telecommunications,2010,17(4):88-93

[8] 郑勋烨,黄晶晶.基于支持向量回归机的交通状态短时预测和北京某区域实例分析[J].数学的实践与认识,2010,40(10):76-85

[9] 李自珍,白 玫,黄 颖.BP网络和RBF网络在期货预测中的比较研究[J].数学的实践与认识,2008,38(1):60-64

[10] 隆金玲.Sum-of-Product神经网络和径向基函数神经网络逼近能力研究[D].大连:大连理工大学,2008

[11] Vahid Fathi,Gholam Ali Montazer.An improvement in RBF learning algorithm based on PSO for real time applications[J].Neurocomputing,2013,111(2):169-176

[12] George E.Tsekouras.A simple and effective algorithm for implementing particle swarm optimization in RBF network’s design using input-output fuzzy clustering.Neurocomputing,2013,108(2):36-44

[13] Sun J,Feng B,Xu W.Particle swarm optimization with particles having quantum behavior[C]//Evolutionary Computation,2004.CEC2004.Congress on.IEEE,2004,1:325-331

[14] J.Sun,W.Fang,V.Palade,et al.Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point[J].Applied Mathematics and Computation, 2011,218(7):3763-3775

[15] 孔丽丹,孙 俊,须文波.基于全局层次的自适应QPSO算法[J].计算机工程与应用,2007,43(26):50-53

[16] 朱文婕,吴 楠,胡学钢.一个改进的模糊聚类有效性指标[J].计算机工程与应用,2011,47(5):206-209

[17] 张 敏,于 剑.基于划分的模糊聚类算法[J].软件学报,2004,15(6):858-868

A QPSO-RBF Neural Network Based Traffic flow Prediction Method

Wang Wei

(Mathematics School of Jinzhong University,Jinzhong 030600, China)

A method based on neural network improved with novel quantum behaved particle swarm optimization algorithm was proposed in this paper, for the aim of optimizing the neural network’s weight and threshold, the training sample was optimized with cluster algorithm to optimize the training course. Simulation was carried out at last, and the result shows that this method can get high precision in predicting short time traffic flow, and the error is stably, it could be served as a new reference for the application of traffic flow prediction.

RBF neural network; quantum behaved particle swarm optimization algorithm; traffic flow; prediction

2015-01-21

王 惟(1987-)，女，晋中学院数学学院助教，主要从事人工智能算法的研究.

1672-2027(2015)02-0028-05

O29

A