3维Minkowski空间中的特殊直纹面
刘作栋,姜淼鑫,陈 亮
(东北师范大学数学与统计学院,吉林 长春130024)
直纹面是由一条直线连续移动所形成的特殊曲面,因其在物理学、运动学中的重要应用而引起众多几何学家和物理学家的兴趣.如:文献[1]研究了欧氏空间中由特殊曲线生成的直纹面;文献[2]对于Minkowski空间中的直纹面进行细致的分类;裴东河等人则从奇点理论的角度对3维Minkowski空间中由特殊曲线及非类光曲线生成的可展曲面的性质进行了研究[3-4].
本文主要研究3维Minkowski空间中以非类光曲线为导线,以该曲线的修正达布向量为母线的直纹面的微分几何性质.文中所涉及的曲线和映射都是C∞的.
1 三维Minkowski空间中的基本概念
称具有伪度量ds2=dx2+dy2-dz2的三维向量空间为三维Minkowski空间或者三维伪欧氏空间,记为M31.设

是M31中的两个向量,分别定义它们的伪内积和伪外积为

分别称M31中的非零向量α=(x,y,z)为类空向量、类光向量或类时向量,如果〈α,α〉>0,〈α,α〉=0或〈α,α〉<0.其中类空向量和类时向量统称为非类光向量.对于M31中的非类光向量α=(x,y,z),定义向量α 的范数为

其中

若‖α‖=1,则称α 为单位向量.
设γ:I→M31,γ(t)=(x(t),y(t),z(t))是M31中的正则曲线,其中I是一个开区间.对任意的t∈I,如果曲线γ 的切向量为类空向量、类光向量或类时向量,则分别称曲线γ 为类空曲线、类光曲线或类时曲线,类空曲线和类时曲线统称为非类光曲线.
对于M31中的非类光曲线γ,引进弧长参数

则

记t(s)=γ′(s)为γ 在点s处的切向量,记曲线γ 在点s处的曲率函数为


特别的,当ω(γ)=1,ε=1时,曲线γ 为第一类空曲线;当ω(γ)=1,ε=-1时,曲线γ 为第二类空曲线;当ω(γ)=-1,ε=-1时,曲线γ 为类时曲线.
定义1.1[5]设t(s)是非类光曲线γ:I→M31的切向量,α 是一固定的向量,若〈t(s),α〉等于一常数,我们则称γ 为Minkowski空间中的一般螺线.特别的,M31中的曲线γ 为一般螺线,如果τ/κ为常数;γ为圆柱螺线,如果κ,τ分别都是常数.
定义1.2 对于M31中的非类光曲线γ,称D(s)=-(τ/κ)(s)t(s)+ω(γ)b(s)为γ 的修正达布向量.
三维Minkowski空间中的直纹面记为r(s,v)=α(s)+vβ(s),称α(s)为直纹面的导线,β(s)为直纹面的母线.特别的,如果β(s)是常向量,则称直纹面为柱面;如果α(s)是常向量,则称直纹面为锥面.直纹面两条相邻母线的公垂线的垂足极限点称为腰点,腰点的轨迹称为腰线.一般腰线的参数表达式为特别的,如果导线为腰线,则有〈α(s)′,β(s)′〉=0.
定义1.3 设r(u,v)是3维Minkowski空间中的曲面,若ru×rv(u0,v0)=0,则称(u0,v0)为曲面r(u,v)的奇点.
定义1.4 设δ(s)为3维Minkowski空间中直纹面r(s,v)上的曲线,如果δ(s)′=0,则称δ(s)为该直纹面的奇线,奇线上的点称为二阶奇点.
如果(α′,β,β′)=0,我们称直纹面r(s,v)=α(s)+vβ(s)为可展曲面.与欧氏空间类似,3 维Minkowski空间中的可展曲面是柱面、锥面或切线曲面的一种[6].
命题1.1[7]3维Minkowski空间中的曲面为可展曲面的充分必要条件是它的高斯曲率恒为零.
命题1.2[8]3维Minkowski空间中的曲面上的曲线为曲率线的充分必要条件是沿此曲线的曲面的法线组成一可展曲面.
2.主要结论及证明
设α(s)为3维Minkowski空间中的非类光曲线,D(s)是其修正达布向量,则以α 为导线,以D 为母线的直纹面为
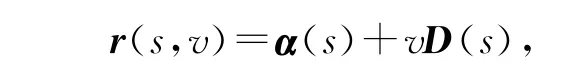
其第一基本型为

其中:


其第二基本型为

其中:

则该直纹面的高斯曲率

即该直纹面为可展曲面.平均曲率

腰线

其中ω(α)=sign(t(s)).
定理2.1 在M31中,设α(s)为非类光曲线,则下列结论成立:
(1)α 是直纹面r(s,v)=α(s)+vD(s)的测地线.
(2)α 是直纹面r(s,v)=α(s)+vD(s)的曲率线当且仅当α 的挠率τ=0.
证明 (1)由测地线的定义,如果曲面上的曲线是测地线,那么该曲线上各点的主法线与曲面在该点处的法线相同.根据上述计算可知,直纹面r(s,v)=α(s)+vD(s)在导线α(s)上各点的法线与曲线的主法线重合,得证.
(2)如果曲面上的曲线是曲率线,由命题1.2可知,以该曲线为导线,以曲面沿着该曲线的单位法向量为母线方向的直纹面为可展曲面.又因为在直纹面r(s,v)=α(s)+vD(s)上,沿着α 的曲面的法向量和α 的主法向量n 是共线的,因此该可展曲面可写为~r(s,v)=α(s)+vn.所以(α′(s),n,n′)=0,因此τ=0;反之显然成立.
定理2.2 设α(s)是M31中的圆柱螺线,则直纹面r(s,v)=α(s)+vD(s)为极小曲面的充分必要条件是τ2=-ω(α)κ2,其中ω(α)=sign(t(s)).
证明 因为

又由于导线α(s)是圆柱螺线,根据定义1.1,则有τ,κ均为常数.因此,

为常数.若直纹面r(s,v)=α(s)+vD(s)为极小曲面,则有H=0.经过计算可知,τ2=-ω(α)κ2.反之,如果τ2=-ω(α)κ2,则以圆柱螺线为导线的直纹面r(s,v)=α(s)+vD(s)的平均曲率为零,即为极小曲面.
定理2.3 在M31中,设α(s)为非类光曲线,则(s,v)为直纹面r(s,v)=α(s)+vD(s)的二阶奇点的充要条件是其中a,b为常数.
证明 根据定义1.3,如果(s0,v0)为直纹面r(s,v)=α(s)+vD(s)的奇点,则
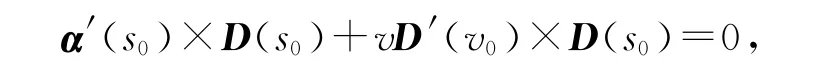
不妨取导线α 为类空曲线,根据Frenet-serret型公式有[1-v0(τ/κ)′(s0)]n(s0)=0.而该方程有解的充要条件是(τ/κ)′(s0)≠0,v0=[(τ/κ)′(s0)]-1,即直纹面r(s,v)=α(s)+vD(s)的奇线方程为δ(s)=α(s)+[(τ/κ)′(s0)]-1D(s).
令δ(s)′=0,则

当导线α 为类时曲线时有相同的结论.
定理2.4 在M31中,设α(s)为非类光曲线,r(s,v)=α(s)+vD(s)是以α(s)为导线,以α(s)的修正达布向量D(s)为母线的直纹面,则下列条件等价:
(1)直纹面r(s,v)是一个正则曲面;
(2)非类光曲线α(s)是一般螺线;
(3)直纹面r(s,v)是柱面.
证明 (1)⇒(2).由定理2.3,直纹面为正则曲面当且仅当对任意的s,(τ/κ)′(s)=0,即非类光曲线α(s)是一般螺线.
(2)⇒(3).非类光曲线α(s)是一般螺线,有(τ/κ)′(s0)=0,即(τ/κ)(s0)为常数,因此D(s)是常向量,所以直纹面r(s,v)=α(s)+vD(s)为柱面.
(3)⇒(1).直纹面r(s,v)=α(s)+vD(s)是柱面当且仅当D(s)为常向量,即(τ/κ)=常数,因此(τ/κ)′(s0)=0,所以直纹面r(s,v)为正则曲面.
注2.1 文献[9]中的命题1是上述定理2.4的特殊形式.
[1]ALI AT,ABDEL AZIZ HS,SOROUR AH.Ruled surface generated by some special curves in Euclidean 3-space[J].Journal of the Egyptian Mathematical Society,2013,21(3):285-294.
[2]KIM YH,YOON WD.Classfication of ruled surfaces in Minkowski space[J].J Geom Phys,2004,49(1):89-100.
[3]王志刚,吕永震,裴东河,等.三维Minkowski空间中的特殊曲线和可展曲面[J].东北师大学报:自然科学版,2008,40(2):1-6.
[4]姜扬,裴东河.三维Minkowski空间中非类光曲线的从切可展曲面的奇点分类[J].东北师大学报:自然科学版,2007,39(1):22-27.
[5]赵广宇.三维Minkowski空间中一般螺线的几何性质[D].长春:东北师范大学,2006.
[6]刘锦兰.三维Minkowski空间中非可展直纹面的分类[D].大连:大连理工大学,2008.
[7]DILLEN F,KUHNEL W.Ruled weingarten surfaces in Minkowski 3-space[J].Manuscripta Math,1999,98(3):307-320.
[8]李丽.关于三维Minkowski空间中直线汇与焦曲面的对应关系[D].大连:大连理工大学,2005.
[9]ALPER OSMAN,HANDAN B,MAHMUT E.On the ruled surface in Minkowski 3-space[J].Journal of Zhejiang University Science A,2006,7(3):326-329.

