一类具有1∶-3共振奇点的复七次系统的可积性条件
桑 波
(聊城大学数学科学学院,山东 聊城252059)
1 研究背景
当线性孤立奇点是中心时,其非线性项的影响可使相图是非退化中心,或稳定焦点,或不稳定焦点,这类判定问题称为中心焦点问题.自1904年H.Dulac研究二次系统的中心判定以来,中心焦点问题受到一些学者的广泛关注.它对Arnold问题、可积性问题和Hilbert第16问题后半部分的解决都具有重要意义.N.N.Bautin完整解决了二次系统的中心焦点判定问题;K.S.Sibirskii解决了缺少二次项的三次系统的中心判定问题;A.P.Sadovskii和T.V.Shcheglova利用Cherkas方法解决了一类可约化为Liéard系统的三次系统的中心判定问题[1].但对于一般三次及三次以上系统,目前还没有彻底的结论.
H.Zoladek将中心问题推广到具有p∶-q共振奇点的复多项式微分系统[2]

其中p,q∈N;(p,q)=1;x,y,t∈C.而且

尽管对于p∶-q=1∶-1,p∶-q=1∶-2,p∶-q=1∶-3,p∶-q=2∶-3,p∶-q=1∶-q等情形下的特殊多项式系统的可积性问题,已有大量的研究成果[3-10],但对于高次多项式系统的可积性问题,仍需作进一步的研究.
对于系统(1),由文献[11],可逐项确定形式幂级数

使得

其中Wn称为系统(1)在原点的第n阶广义奇点量,其计算方法见文献[12].
引理1[13]系统(1)在原点可积的充要条件是该系统存在如(2)式的形式首次积分.
2 主要结果及其证明
考虑一类以原点为1∶-3共振奇点的复七次系统
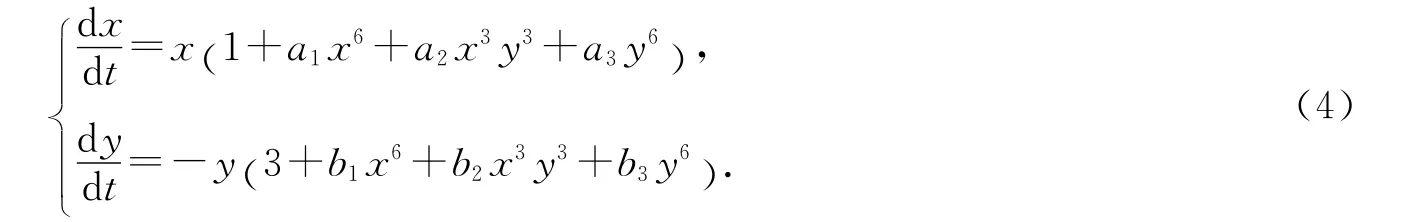
通过计算,我们得到系统的前9阶广义奇点量W1,W2,…,W9.其中:

定理1 系统(4)在原点可积的充要条件是下列八组条件之一成立:
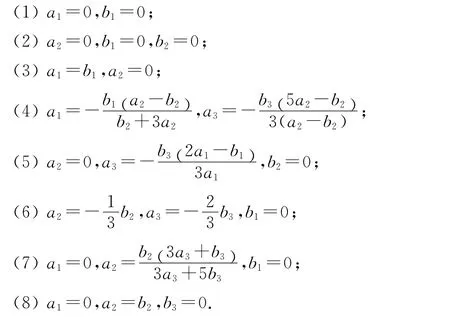
证明 必要性只需在次数反字典序tdeg (a3,b3,a2,b2,a1,b1)下,计算前9 阶广义奇 点量的Gröbner基[14]

然后使用无特征集法对多项式组G 进行完全零点分解,便得到定理中的8组系数条件.
充分性 条件(1)成立时,系统(4)化为


当vn-6(x),vn-3(x)取定时,上述递推公式是关于未知函数vn(y)的一阶线性方程.令v-5(x)=v-4(x)=…=v0(x)=0,通过逐项求解,我们依次得到

然后通过数学归纳法和递推公式,不难证明vn(x)是次数为3n 的多项式.因此系统(5)具有形式首次积分,由引理1,系统是可积的.
当条件(2)成立时,系统(4)变为

当条件(3)成立时,系统(4)变为



令v-5(x)=v-4(x)=…=v0(x)=0,通过逐项求解,我们依次得到

当条件(4)成立时,系统(4)变为

当条件(5)成立时,系统(4)变为

当条件(6)成立时,系统(4)变为

当条件(7)成立时,系统(4)变为
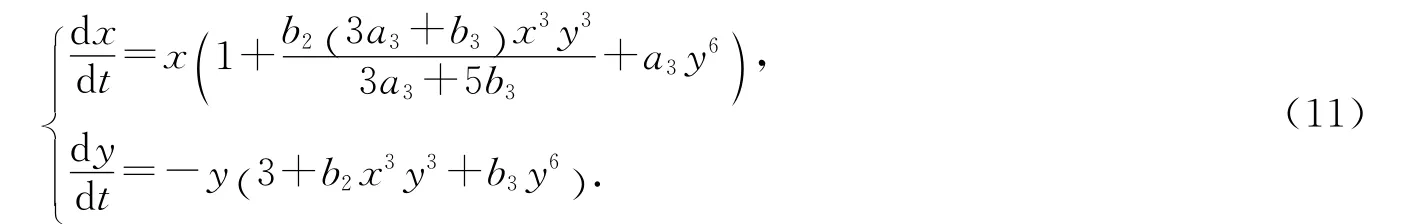
当条件(8)成立时,系统(4)变为

[1]SADOVSKII A P,SHCHEGLOVA T V.Solutions of the center focus problem for a nine-parameter cubic system[J].Differential Equations,2011,47(2):208-223.
[3]ROMANOVSKI V G,SHCHEGLOVA N L.The integrability conditions for two cubic vector fields[J].Differential Equations,2000,36(1):108-112.
[4]FERˇCEC B,GINÉJ,LIU Y R,et al.Integrability conditions for Lotka-Volterra planar complex quartic systems having homogeneous nonlinearities[J].Acta Appl Math,2013,124(1):107-122.
[5]GINÉJ,ROMANOVSKI V G.Integrability conditions for Lotka-Volterra planar complex quintic systems[J].Nonlinear Analysis:Real World Applications,2010,11(3):2100-2105.
[6]FERˇCEC B,CHEN X W,ROMANOVSKI V G.Integrability conditions for complex systems with homogeneous quintic nonlinearities[J].Journal of Applied Analysis and Computation,2011,1(1):9-20.
[7]LIU C J,CHEN G T,CHEN G R.Integrability of Lotka-Volterra type systems of degree 4[J].Journal of Mathematical Analysis and Applications,2012,388(2):1107-1116.
[8]GINÉJ,CHRISTOPHER C,PRESERN M,et al.The resonant center problem for a 2∶-3resonant cubic Lotka-Volterra system[C].Maribor:CASC,2012:129-142.
[9]CHEN X W,GINÉJ,ROMANOVSKI V G,et al.The 1∶-qresonant center problem for certain cubic Lotka-Volterra systems[J].Applied Mathematics and Computation,2012,218(23):11620-11633.
[10]HU Z P,ROMANOVSKI V G,SHAFER D S.1∶-3resonant centers on C2with homogeneous cubic nonlinearities[J].Computers and Mathematics with Applications,2008,56(8):1927-1940.
[11]刘一戎,李继彬.平面向量场的若干经典问题[M].北京:科学出版社,2010:10-113.
[12]SANG B.Center problem for a class of degenerate quartic systems[J].Electronic Journal of Qualitative Theory of Differential Equations,2014,74:1-17.
[13]MATTEI J F,MOUSSU R.Holonomie et intégrates premières[J].Ann Sci Ecole Normale Superieure,1980,13(4):469-523.
[14]刘木兰.Gröbner基理论及其应用[M].北京:科学出版社,2000:97-112.

