浦肯野神经元回路中的同步性研究*

张煦晨 刘深泉 任会霞

(华南理工大学理学院应用数学系，广州 510640)

引言

同步性活动是大脑神经系统中一种非常常见与普遍的生理学现象［1-3］，同时它也被证明与大脑中许多认知功能有着密切的联系，例如:时间聚焦与空间聚焦［4］，学习与记忆［5］，观察意识［6］，睡眠与知觉感应［7-8］等.另外，同步性活动也与许多中枢神经的疾病有着密切的关系，例如:帕金森综合症［9］，癫痫病［8］，精神分裂症［10］，阿兹海默症［10］.因此，对于神经回路中神经元之间同步性的研究就变得十分重要，只有掌握了神经元之间同步性的性质才能更好的调节神经元的信息传递功能.

浦肯野神经元对于小脑的运动调节起着不可替代的作用，同时它也影响到人类大量的疾病，包括酒精中毒，自身免疫系统疾病和基因变异疾病等.在过去关于浦肯野神经元同步性的研究中，Shin S-L的研究小组主要通过动力学分析来研究浦肯野神经元的自身发放特性，进而得到关于时间聚焦［11］和回传序列［12］的相关性质;Servais L和Cheron G的研究显示浦肯野神经元的韵律性和同步性特征可以用来调节小脑的快速振荡，并且它对反馈回传具有积极的促进作用［13］;而Sergio S和Philippe L则分别通过实验与模型的方法研究了颗粒神经元与浦肯野神经元突触连接的相关性质，因为该突触被认为与信息的储存与传递密切关联［14-15］;基于此，本文主要就浦肯野神经元分别与盘状纤维和颗粒神经元之间的同步性进行分析.

浦肯野神经元主要与盘状纤维和颗粒神经元形成兴奋性突触连接，但是由于不同神经元之间突触连接的固有性质存在显著性差异，所以不同神经元之间的同步性也必不相同.在本文中，通过建立与实际神经系统非常相似的神经回路，我们主要研究不同神经元在化学突触下的同步性问题.数值结果显示神经元之间突触的连接强度与浦肯野神经元树突上CaP电导系数对神经元之间的同步性有着显著影响.

1 模型与方法

本文构建的小鼠浦肯野神经元回路模型共包括4种神经元:浦肯野神经元，颗粒神经元，攀状纤维，高尔基神经元.如图1所示，175根平行纤维分别连接到浦肯野神经元远端的175根树突上;攀状纤维的1根轴突缠绕在浦肯野神经元近端树突的主轴上，形成13个突触连接［16］;高尔基神经元的10根树突与10根平行纤维相连接，另外10根轴突与颗粒神经元的10根树突相连接，颗粒神经元通过平行纤维对高尔基神经元会产生兴奋性刺激，高尔基神经元则通过突触的连接给颗粒神经元抑制性的反馈作用.注意:由于未能找到Mouse的攀状纤维的结构与离子通道的相关参数，所以本文借用Rat的攀状纤维代替Mouse的攀状纤维做相关的模型建立于运算.

基于小脑皮层的解剖实验［17-18］，小脑皮层神经网络中每种神经元之间的突触连接关系［19］以及各种神经元Hodgkin-Huxley模型化的电生理参数［20］，浦肯野神经元回路中神经元的层次结构是十分鲜明的，各种神经元在回路中的结构也是有序排列的.在理论的网络模型分析中，每个简单的神经元模型都被描述成一个依靠传导的模型并且每一个神经元的形态都可以用房室模型来刻画，神经元内电信号传递的基本理论是Rall的电缆模型.例如在本文中，蒲肯野神经元就包括胞体与树突，根据不同形态特征，不同的神经元部分可以用不同的房室数量来描述，具体的模型建立与方程见文献［21］.

本文运用NEURON软件来模拟浦肯野神经元回路模型，运用MATLAB软件来对数据进行处理.数值模拟的结果经过多次演算，证明是正确的.

图1 浦肯野神经元回路模型Fig.1 The model of Purkinje cell circuit

2 模拟结果与分析

2.1 相位响应曲线的研究

相位响应曲线主要是用来分析周期性发放神经元的固有性质与振荡行为［22］，神经元的相位响应曲线可以根据神经元的兴奋性分类:只有正值的部分(type 1-like神经元)和有负值的部分(type 2-like神经元).更重要的是，相位响应曲线的类型能够显示输入-输出的功能以及同步性行为:在网络模型中属于type 2-like的神经元能够通过突触连接来调节它们的同步性活动，但是type 1-like神经元却不行［23］.

相位响应曲线是测量神经元下一个峰发放的时间.当神经元在某个时间点受到突然的短暂刺激时，如果神经元呈周期性发放并且它的ISI(峰峰间距)为T，t是上一个峰发放的时间，A是短暂刺激的强度，T'(A，t)是刺激后下一个峰发放的时间，注意T'(0，t)=T是基准的发放频率，则相位响应曲线如下:

在图2中，三种不同神经元的相位响应曲线各不相同，浦肯野神经元与颗粒神经元的相位响应曲线全部数值都是非负的，而盘状纤维的相位响应曲线部分数值是负的.再根据f-I曲线我们已经判断了浦肯野神经元与颗粒神经元属于type 1-like神经元，而盘状纤维属于type 2-like神经元.通过对比可以看到，随着外界刺激电流的不断增加浦肯野神经元和颗粒神经元的相位响应曲线的变化幅度都在不断的增加，而盘状纤维的相位响应曲线的数值则是从非负逐渐变化到正、负值都存在的现象，并且正值逐渐增加，负值逐渐减小.如下图所示:

图2 相位响应曲线，a)浦肯野神经元，b)盘状纤维，c)颗粒神经元;从“o”，“+”，“*”到“□”表示外界刺激的逐渐增加Fig.2 Phase Response Curve，a)Purkinje cell，b)climbing fiber，c)granule cell;from“o”，“+”，“*”to“□”represent the increase of external stimuli

2.2 浦肯野神经元-颗粒神经元回路中的同步性

为了描述两个耦合神经元之间的同步性关系，本节首先引进相关系数来衡量两个神经元之间的同步性程度［24］，相关系数表示如下:

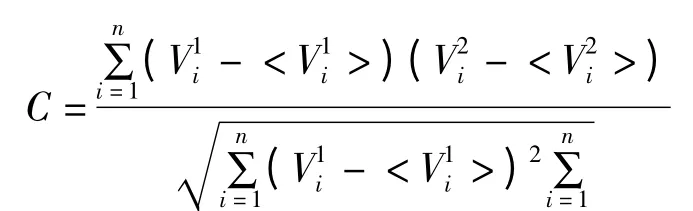
除了相关系数之外，本节将引用另一指标来衡量神经元之间的同步性强弱，称之为神经元膜电位平均差值|V1-V2|peak.计算步骤如下:首先得到神经元膜电压V1和V2绝对值(记作:|V1-V2|)，如图3所示.普遍而言，任意时刻|V1-V2|的峰值(记作:|V1-V2|peak)也是各不相同，如果两个神经元之间的完全同步的，那么|V1-V2|peak的平均值等于0，当|V1-V2|peak的平均值越大时，神经元之间的非同步性越明显.

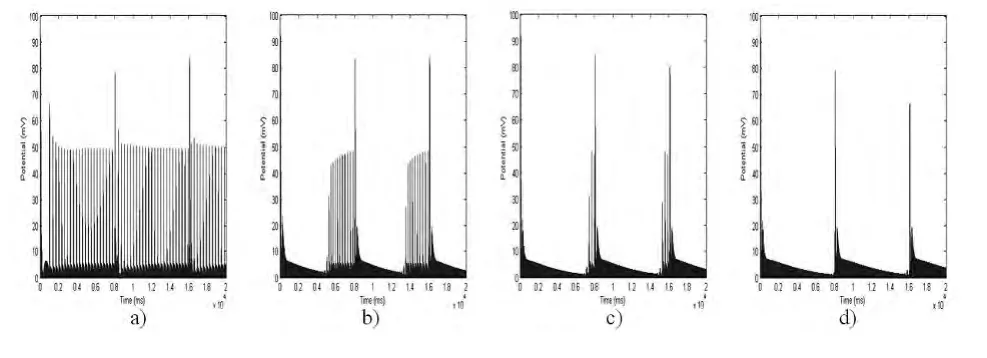
图3 浦肯野神经元与颗粒神经元膜电位的绝对差值，a)-d)gsyn分别是0，0.3，0.6，0.9(mS/cm2)ig.3 Absolute difference of the membrane potentials between Purkinje neuron and granule neuron under different gsyn，a)-b):gsyn are 0，0.3，0.6，0.9(mS/cm2)

图4 (a)|V1-V2|peak的平均值，(b)同步性相关系数Fig.4 Diagram of(a)mean value of|V1-V2|peak，(b)correlation coefficient

图5 (a)|V1-V2|peak的平均值，(b)同步性相关系数Fig.5 Diagram of(a)mean value of|V1-V2|peak，(b)correlation coefficient

首先我们来研究浦肯野神经元-颗粒神经元回路中的同步性现象.由于钙离子在小脑中起着重要的作用，它与许多功能紧密联系在一起，所以我们先改变神经元之间突触的连接强度与浦肯野神经元中树突上CaP电导系数，从不同方面来研究浦肯野神经元回路中的同步性现象.

如图4所示，可以看到随着电导系数的不断增加，浦肯野神经元与颗粒神经元|V1-V2|peak的平均值逐渐减小，在达到相对稳定的状态后开始缓慢上升，在这个过程中，其对应的相关系数则是在达到某一最大值后也开始下降，最后通过这两种指标都可以看出随着浦肯野神经元与颗粒神经元之间电导系数的不断增加，这两种神经元之间的同步性在逐渐增强，当电导系数超过某一临界值时，同步性逐渐减弱.

相比于突触连接的电导系数对于同步性的影响，浦肯野神经元树突上CaP电导系数对于它们之间的同步性影响也表现出相似的规律性变化.如图5所示，随着CaP电导系数的增加，浦肯野神经元与颗粒神经元|V1-V2|peak的平均值呈现振荡性变化，在达到稳定状态后逐渐增加;同样地其对应的相关系数也呈现振荡性的变化，只是在CaP电导系数逐渐增加到某一范围内，它们之间的相关系数才会有明显的增加，同步性也随之变强，但是在其它参数范内下，这两种神经元之间并没有保持较高的同步性.

2.3 浦肯野神经元-盘状纤维回路中的同步性

在之前的分析中，本文已经得到了盘状纤维与浦肯野神经元是属于不同类型的兴奋性神经元，而盘状纤维对于浦肯野神经元在信号传递上的“修饰作用”依旧不可忽视，所以本文依然研究它们之间的突触强度与浦肯野神经元树突上CaP电导系数的影响.

图6 (a)|V1-V2|peak的平均值，(b)同步性相关系数Fig.6 Diagram of(a)mean value of|V1-V2|peak，(b)correlation coefficient

图6是盘状纤维与浦肯野神经元之间突触电导系数的变化对它们同步性的影响，随着它们之间突触电导系数的不断增加，浦肯野神经元与盘状纤维之间的|V1-V2|peak的平均值总体上呈现上升趋势，但当突触电导系数到达1.2(mS/cm2)时，立刻下降，然后又逐渐增加，对于与b)中这两种神经元之间的相关系数达到最大值，可见在这一参数意义下，盘状纤维与浦肯野神经元的同步性达到最大.

图7 (a)|V1-V2|peak的平均值，(b)同步性相关系数Fig.7 Diagram of(a)mean value of|V1-V2|peak，(b)correlation coefficient

在图7中，随着浦肯野神经元树突上CaP电导系数的不断增加，浦肯野神经元与盘状纤维之间的|V1-V2|peak的平均值总体上呈现上升趋势，在某一特定的参数范围内出现短暂的降低过程，这一范围对应于b)中两种神经元相关系数短暂的上升期，可以看到CaP电导系数对应浦肯野神经元与盘状纤维之间的同步性起着关键作用，随着CaP电导系数的不断增加，它们之间的相关系数已经达到了0.7-0.8之间.

3 讨论

基于与实际小脑浦肯野神经元回路十分相似的模拟回路，通过研究不同神经元丰富发放特性，本文主要分析了浦肯野神经元回路中不同神经元的相位响应曲线和不同神经元之间的同步性现象.得到如下结论:

1.浦肯野神经元回路中的三种神经元属于不同的兴奋类型:浦肯野神经元和颗粒神经元属于type 1-like神经元，而盘状纤维属于type 2-like神经元，通过她们的相位响应曲线(PRC)可以看出，浦肯野神经元和颗粒神经元的PRC的数值都是非负的，而盘状纤维的则是正、负都有，并且随着外界刺激电流的不断增大，它们PRC的变化幅度都会朝着相应正、负的方向随之增大.

2.浦肯野神经元回路中不同神经元之间的同步性有着显著差异，但是神经元之间的突触电导与浦肯野神经元树突上的CaP电导系数对于它们的同步性也都有重要影响.随着突触电导系数与CaP电导系数的不断增加，神经元之间的同步性都是从弱变强，并在某一参数范围内达到稳定状态，然后同步性又会开始减弱，也就是说神经元之间良好的同步性需要对突触电导系数与CaP电导系数进行良好的控制.

在上述讨论中，本文只是考虑了神经元之间的相关性的同步分析，并没有检验它们的相位对应性以及发放频率的同步性，所以我们首先分析了不同神经元之间的相位响应曲线(PRC)，因为相位响应曲线被认为与神经元之间的同步性有着密切联系，我们将在未来的工作中进一步用相位响应曲线来分析不同神经元之间的同步性性质.

1 Seidenbecher T，Laxmi T R，Stork O，Pape H C，Amygdalar and hippocampal theta rhythm synchronization during fear memory retrieval.Science，2003，301:846～850

2 Singer W，Engel A K，Kreiter A K，et al.Neuronal assemblies:necessity，signature and detectibility.Trends in Cognitive Sciences，1997，20:252～261

3 Toshio A，Takaaki A，Possible role of synchronous input spike trains in controlling the function of neural networks.Neurocomputing，2004，58:259～264

4 Matthew A S，Marc A S，Spatial and temporal scales of neuronal correlation in visual area V4.The Journal of Neuroscience，2013，33(12):5422～5432

5 Gui X，Qi D，Chuan S C，et al.，Complementary role of frontoparietal activity and cortical pattern similarity in successful episodic memory encoding.Cerebral Cortex，2012，23(7):1562～1571

6 Buhusi C V，Meck W H.What makes us tick?Functional and neural mechanisms of interval timing.Nature Reviews Neuroscience，2005，6(10):755～765

7 Emmanuel M，Shahrad T and Seiji N.Sleeping with the hypothalamus:emerging therapeutic targets for sleep disorders.Nature Neuroscience，2002，5，1071～1075

8 Igor T，Maxim B，Josée S，Terrence S.Jasper＇s basic mechanisms of the epilepsies:neuronal synchronization and thalamocortical rhythms in sleep，wake and epilepsy(4th Edition).Bethesda:National Center for Biotechnology Information，2012

9 Rubchinsky L L，Park C，and Worth R M.Intermittent neural synchronization in Parkinson＇s disease.Nonlinear Dynamics，2012，68(3):329～346

10 Peter J U，Wolf S.Neural synchrony in brain disorders:relevance for cognitive dysfunctions and pathophysiology.Neuron，2006，52(1):155～168

11 Shin SL，Erik D S.Dynamic synchronization of Purkinje cell simple spikes.Journal of Neurophysiology，2006，96:3485～3491

12 Shin SL，Hoebeek F E，Schonewille M，De Zeeuw C I，Aertsen A，et al.Regular patterns in cerebellar Purkinje cell simple spike trains.PLOSONE，2007，2(5):485～498

13 Servais L，Cheron G.Purkinje cell rhythmicity and synchronicity during modulation of fast cerebellar oscillation.Neuroscience，2005，134(4):1247～1259

14 Sergio S，Reinoud M，Erik D S.Synchronization of Purkinje cell pairs along the parallel fiber axis:a model.Neurocomputing，2003，52，97～102

15 Philippe I，Boris B.Properties of unitary granule cell-Purkinje cell synapses in adult rat cerebellar slices.The Journal of Neuroscience，2002，22(22):9668～9678

16 Jennty T，Chal D，Beverley A C，Michael H.The origin of the complex spike in cerebellar Purkinje cells.The Journal of Neuroscience，2008，28(30):7599～7609

17 Longstaff A.Instant notes in neuroscience.The United Kingdom:Bios Scientific Publishers Limited，2000

18 Bear M F，Connors B W，and Paradios M A.Exploring the Brain.Neuroscience，2001

19 Fabbro F.Introduction to language and cerebellum.Journal of Neurolinguistics，2000，13:83～94

20 Yamada W M，Koch C，and Adams P R.Multiple channels and calcium dynamics:Methods of neuronal modeling.Cambridge:MIT Press，1987

21 汪雷，刘深泉.大脑中神经回路的电位发放比较.动力学与控制学报，2010，8(3):277～283(Wang L，Liu SQ.Comparison of potential spike of neural circuit in the brain.Journal of Dynamics and Control，2010，8(3):277～283(in Chinese))

22 Ermentrout B.Type I membranes，phase resetting curves，and synchrony.Neural Computation，1996，8(5):979–1001

23 Oprisan SA，Prinz A A，and Canavier CC.Phase resetting and phase locking in hybrid circuits of one model and one biological neuron.Biophysical Journal，2004，87:2283～2298

24 Wang Q Y，Duan Z S，Feng Z S，Chen G R，Lu Q S.Synchronization transition in gap-junction-coupled leech neurons.Physica A，2008，387:4404～4410