基于多体动力学的车辆道岔通过性能研究*

朱博文 路永婕 王建西

(1.太原轨道交通装备有限责任公司，太原 030009)(2.石家庄铁道大学机械工程学院，石家庄 050043)(3.河北省交通安全与控制重点实验室，石家庄 050043)(4.石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室，石家庄 050043)

引言

由于道岔结构复杂，特别是其轨道截面形状随线路长度变化而变化，当车辆通过道岔时将会引起较大的动力学响应，甚至导致脱轨.因此，建立车辆—道岔系统模型并对影响其动力学响应特性的因素进行分析成为国内外关注重点.参考文献［1］利用自编仿真程序，对列车直向和侧向通过道岔进行动力学仿真，并讨论线路几何不平顺对其安全性、平稳性的影响，提出并验证了轨道不平顺控制方法及控制标准建议值;参考文献［2］使用SIMPACK软件对机车侧逆向和直逆向通过道岔的动力学响应进行仿真计算，并讨论了机车踏面和道岔部分参数对机车车辆系统动力学性能影响;参考文献［3］采用VAMPIRE软件对货车—道岔系统模型进行仿真计算，研究货车运行方案以实现减少轮轨磨耗的目的.现阶段国内虽然有很多文献对车辆通过道岔进行动力学分析，但通常将轨下视为刚性.

根据道岔变截面特性，本文在多体动力学软件中建立60kg/m钢轨18号可动心轨单开道岔模型和车辆模型，建模时将道岔视为0自由度刚体，在第3节中考虑轨下刚度和阻尼，将车辆视为由刚体组成具有42个自由度的多体系统，建立LM磨耗型踏面模型，利用Kalker接触理论，对模型进行验证.最后分析车辆在道岔区间的动力学响应特性，为提高车辆通过道岔速度、轨下力学参数匹配提供理论依据.

1 建立车辆—道岔系统动力学模型

1.1 道岔模型

道岔建模过程中，关键是描述转辙器区和辙叉区的特征截面，包括60kg/m基本轨截面、尖轨和基本轨、长心轨和短心轨等密贴截面.根据参考文献［4］确定出截面位置，利用CAD绘制出较为准确的特征截面，将截面表面轮廓离散成点，编制数据文件，表达出轨道任意截面形状.由于在CAD中绘制轮廓为轨道密贴截面，因此在绘制特征截面时，不能将轨道顶面最高点作为原点，轨道坐标原点位置与道岔平面布置图有关.图1道岔顶宽30mm尖轨同LM踏面轮轨几何接触关系.

车辆侧向通过道岔时，使用15个截面文件;直向通过道岔时，调用13个截面文件.模拟车辆侧向通过道岔，需要建立4个轨道文件，分别描述踏面、轮缘和轨道接触，车轮背部与护轨接触;直向通过时，只建立2个轨道文件［5］.在动力学软件中建立道岔模型时，其截面变化反映出道岔结构固有不平顺，道岔模型添加德国低干扰谱.轨下按刚性处理，轨底坡1:40，护轨平直段轮缘槽宽度39-42mm.

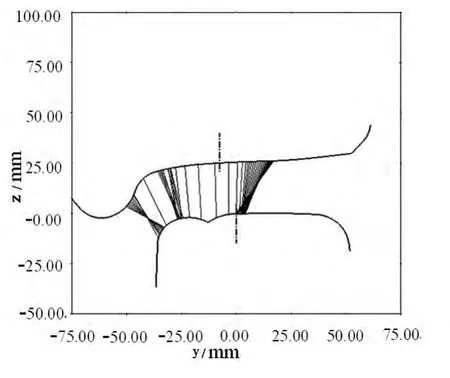
图1 LM踏面与尖轨轮轨接触关系ig.1 Geometric contact relationship between LM tread and switch rail

1.2 车辆模型

由于在车辆系统动力学理论分析模型中无法考虑其中的每一个部件，因此在进行动力学仿真时对车辆动力学性能起主要作用的部件应尽可能仿真其真实工况，而简化次要部件.车体、构架和轮对的弹性比悬挂系统要小得多［6］，故本文中将其视为刚体，根据相关参数建立某型动车组拖车模型.轮使用LM踏面.图2为车辆模型.

图2 车辆模型Fig.2 Multi-body dynamics model of vehicles-turnout

1.3 模型验证

为验证所建模型正确性，本文将仿真结果和参考文献部分结果进行对比，参考文献［7］中仿真分析CRH2C通过曲线线路时动力学响应，参考文献［2］对某型C0-C0机车在道岔区间进行仿真分析.选取参考文献中具有代表性结果与仿真结果进行对比，验证模型准确性.

设置验证曲线半径800m，外轨超高70mm;验证道岔为60kg/m钢轨18号可动心轨道岔.经验证，车辆通过半径为800m曲线和18号可动心轨道岔时，其脱轨系数和轮轨横向力均小于参考文献［2］、［7］计算结果，且符合相关动力学标准.经对比，仿真曲线波形与文献中基本一致，可认为车辆、踏面和道岔模型基本准确.

2 计算结果分析

在多体动力学软件中对车辆模型进行称重计算，其轴重为10.2495t.由于该型动车组拖车车长为25.7m，所以在道岔前设置50m的直线段，因拖车转向架轴距为2.5m，车辆定距为17.5m，所以一位轮对的初始位置为20m.车辆以80km/h的速度，分别在无轨道激励和德国低干扰谱情况下侧向道岔区间.

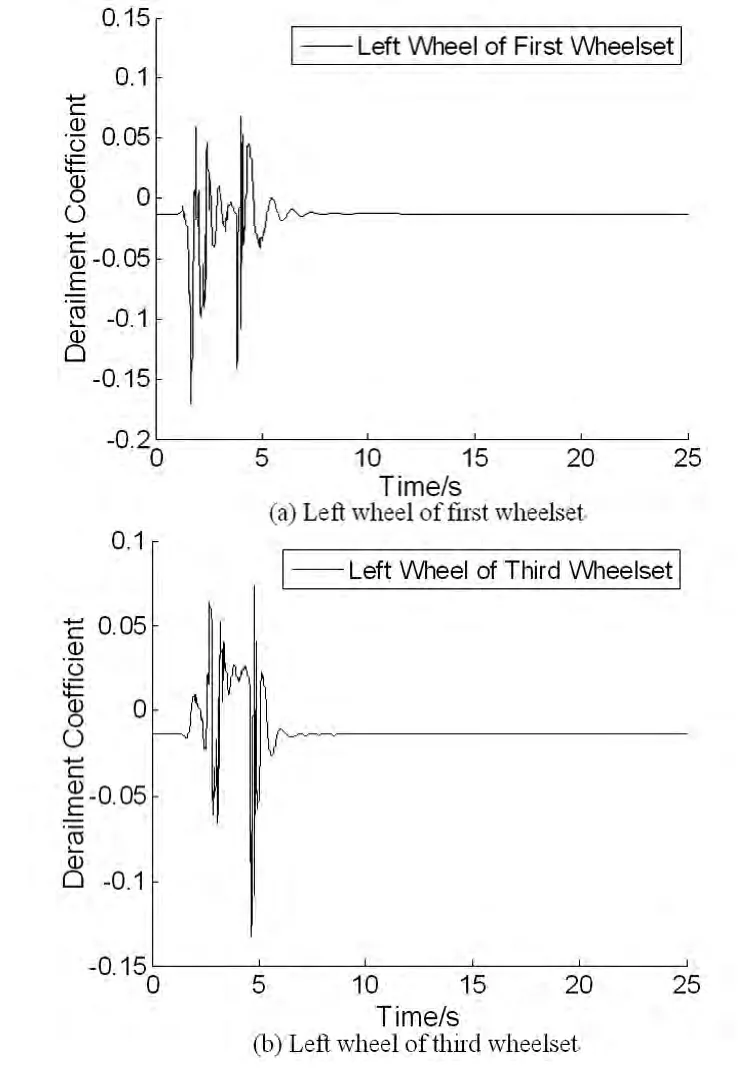
图3 无轨道激励下脱轨系数Fig.3 Derailment coefficient without track spectrum

车辆进入尖轨后，一位和三位轮对左轮的脱轨系数波形发生延迟，前后转向架脱轨系数在不同时间段发生突变.由图3可知.当一位轮对进入尖轨部分时，车轮与钢轨内侧尖轨顶面产生碰撞，轮轨间横向和垂向冲击增大，脱轨系数随之改变.当一位轮对离开尖轨后，脱轨系数逐渐降低.在图3(a)中，有一部分的脱轨系数非常小，此时一位轮对处于导曲线轨上.当一位轮对进入辙叉区之后心轨又会对车轮产生很大的冲击，随后冲击力逐渐降低，当一位轮对离开辙叉区之后，脱轨系数逐渐趋于平缓.无轨道激励的情况下模型脱轨系数最大值为0.2101，小于极限值0.8.在相同条件下，轨道中加入德国低干扰谱.模型脱轨系数最大值为0.3274，小于0.8.通过分析脱轨系数的变化情况可知，脱轨系数的变化是由轨道截面变化和轨道谱造成的，转辙器和辙叉之间有较大脱轨系数.

其次，虽然当前行业发展面临巨大压力，但对优势企业而言并非坏事，大批产能的退出更为市场腾出了空间。倍丰盐湖农业科技的成立整个筹备时间仅有两个月，却准备充分。有两大集团公司的底蕴为支撑，加之前期的合作经验，整体的资源优势、人才储备、渠道网络等各方面准备尤为充分。在大批落后产能退出所提供的发展契机下，山东倍丰看准时机，迅速发力，准确出击，在时机上占到了优势。

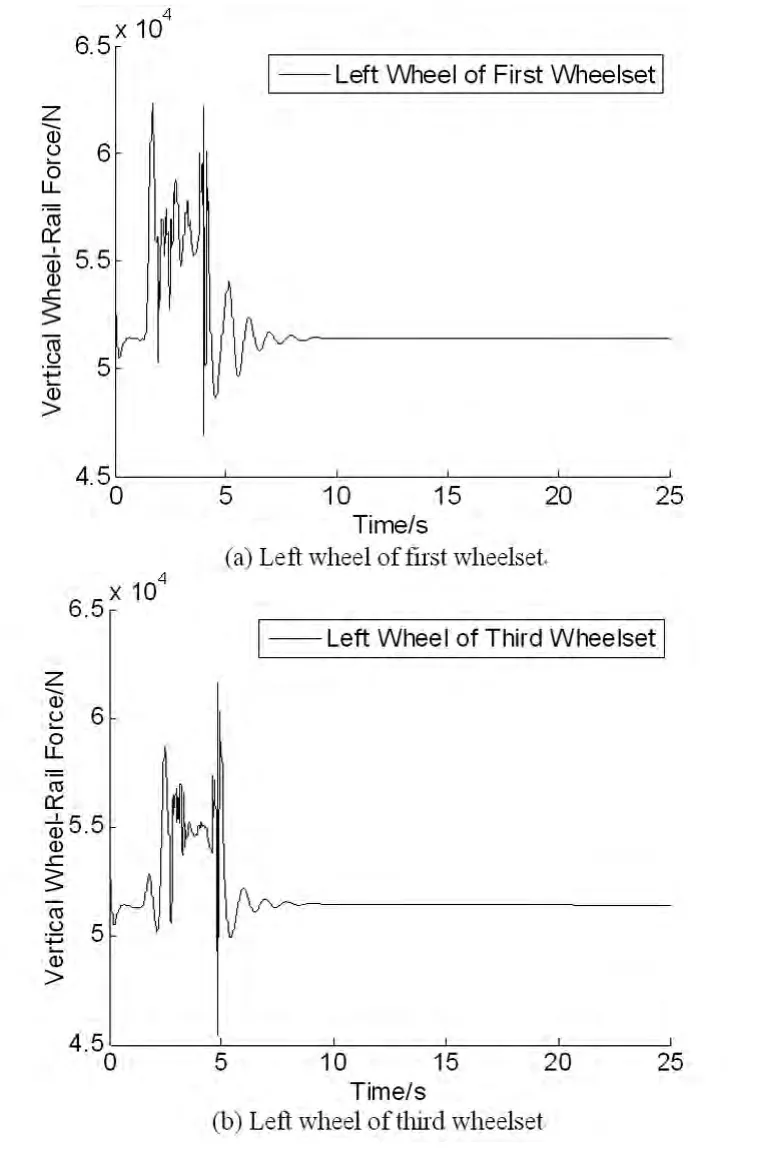
图4 无轨道激励下轮轨垂向力Fig.4 Vertical wheel-rail force without track spectrum

由图4可知，车辆进入转辙器区时，其轮轨垂向力陡升，无轨道激励下其最大值为62.038kN，在转辙器区，由于尖轨的降低值在减小，随着车辆行驶，其轮轨垂向力逐渐降低，当前转向架离开转辙器区，由于后转向架的作用，一位轮对轮轨垂向力仍有较大值58.583kN.进入辙叉区时由于有护轨和心轨的共同作用使其轮轨垂向力再次突变，当车辆离开道岔区间之后轮轨垂向力逐渐趋于平稳.

无轨道激励下，车体横向加速度≤0.6323m/s2，垂向加速度≤0.0834m/s2;有轨道激励情况下，横向加速度≤0.9259m/s2;垂向加速度≤0.2660m/s2，小于限值2.5 m/s2.根据两组车体垂向加速度曲线，在初始阶段车体有一个较大的垂向加速度值，此值为模拟开始时重力加载到车辆上所导致，不具备仿真参考价值，故在计算Sperling指标时截取后20s进行计算.横向Sperling评价指标=0.9071，垂向Sperling评价指标=0.2523;德国低干扰谱下，横向Sperling评价指标=2.0719，垂向Sperling评价指标=1.7116.无激励下，舒适度指标=1.5781;德国低干扰谱下，舒适度指标=2.8144.

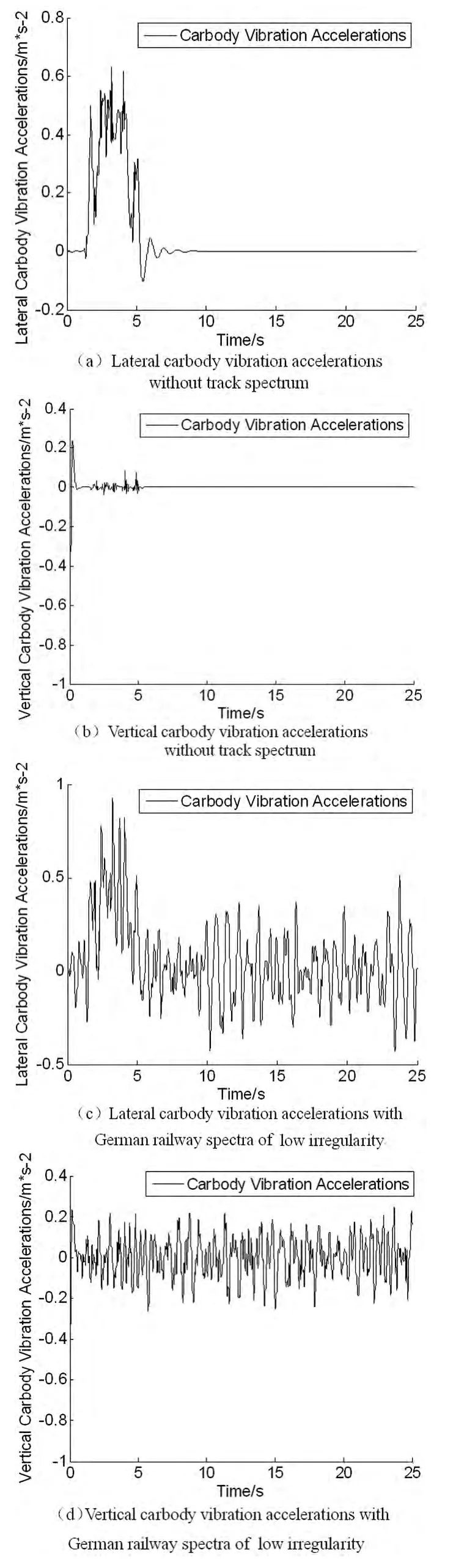
图5 车体加速度Fig.5 Carbody vibration accelerations

在无激励情况下，在t=1.7s左右时，一位轮对左轮与尖轨开始接触，此处轮轨垂向力和轮轴横向力产生突变，车轮抬高量最大值为1.41mm;在t=3.8s左右时，一位轮对开始进入辙叉区，车轮抬高量最大值为1.17mm.

车辆直向通过道岔速度为250km/h，轨道长度改为2000m，以满足车辆在仿真25s内不脱轨.仿真过程不再赘述.车辆侧向和直向通过道岔结果如表1所示.表中Y/Q为脱轨系数(derailment coefficient)，Δp/p为轮重减载率(wheel unloading rate)，Q_w为轮轨垂向力(vertical wheel-rail force)，Y_ws为轮轴横向力(lateral wheelset force)，Yacc为车体横向加速度(lateral carbody vibration accelerations)，Zacc为车体垂向加速度(vertical carbody vibration accelerations)，Ys为横向Sperling指标(lateral Sperling value)，Zs为垂向Sperling指标(vertical Sperling value).

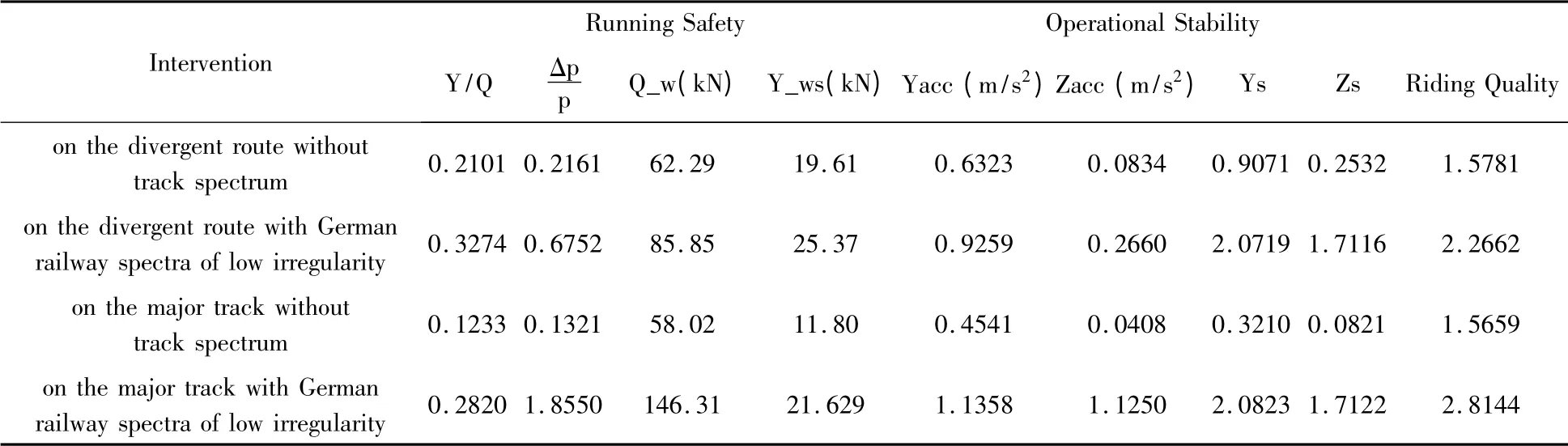
表1 车辆模型在无激励和德国低干谱下侧向、直向通过道岔区间动力学响应Table 1 Comparison results of the dynamics behavior when the vehicle passing through the turnout on the divergent route and on the major track without track spectrum and with German railway spectra of low irregularity

根据表1，在德国低干扰谱下车辆直向通过时，t=0.5625s轮轨垂向力产生一个峰值146.31kN，其余区间轮轨垂向力在80-90kN左右波动，整个运行过程中车轮抬高量最大值为1.33m，虽然此时轮重减载率较大，但车辆仍不脱轨.产生峰值原因如下:(1)由于道岔截面参数不全，截面变化存在奇异点;(2)对于每一级轨道谱，都有建议的客、货车最高运行速度.文章中所加载德国低干扰谱为ICE在速度为200km/h下测得，而仿真速度为250km/h，这种差异性可能导致仿真结果不准确.

3 轨下刚度和阻尼对车辆－道岔系统动力学性能影响

在系统动力学分析建模中，通常方法是把道床和路基作为质量—弹簧—阻尼系统［8］.在此系统中，需要计算道床和路基的振动参数，包括参振质量、弹簧刚度和阻尼器阻尼.

由于国内道岔轨下刚度和阻尼参数不全，故根据参考文献［9］中UIC60-760-1:15道岔轨下力学参数进行设置.同时，由于轨道结构垂向刚度是道岔区轨道结构的主要特征，故保持车辆和道岔其它参数不变，将轨下垂向刚度从2x107N/m以每级1x107N/m幅度递增加到6x107N/m［10］，对比分析在无轨道激励和德国低干扰谱下，轨下垂向刚度变化对车辆—道岔耦合系统动力学性能影响.

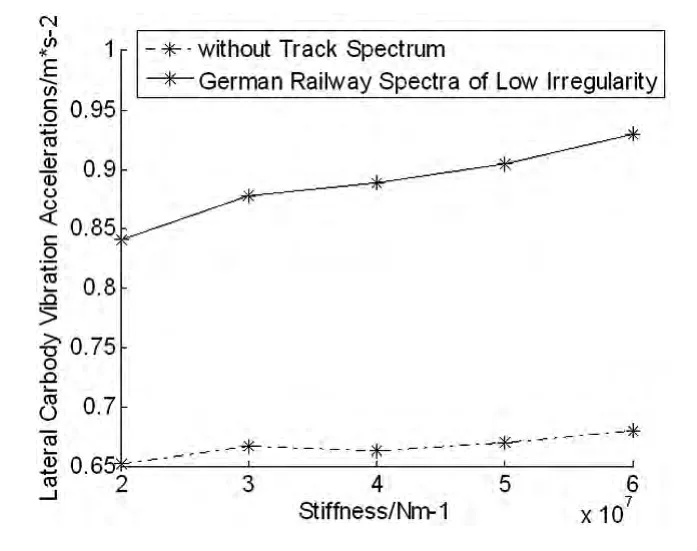
图6 车体横向加速度Fig.6 Lateral carbody vibration accelerations

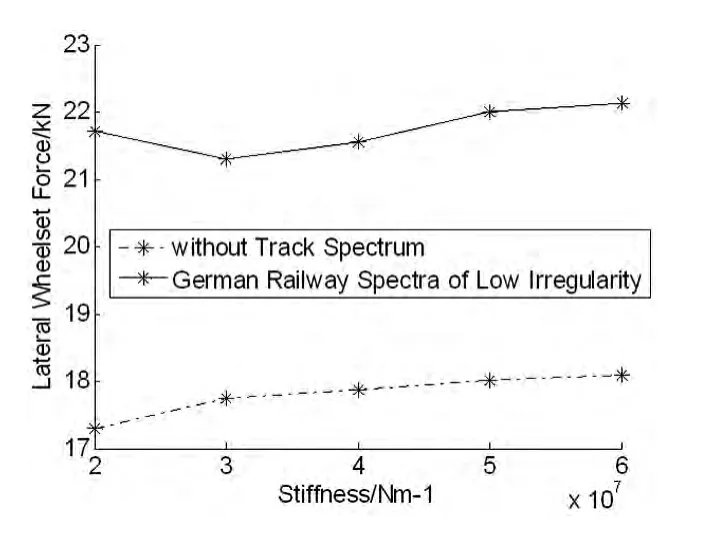
图7 轮轴横向力Fig.7 Lateral wheelset force

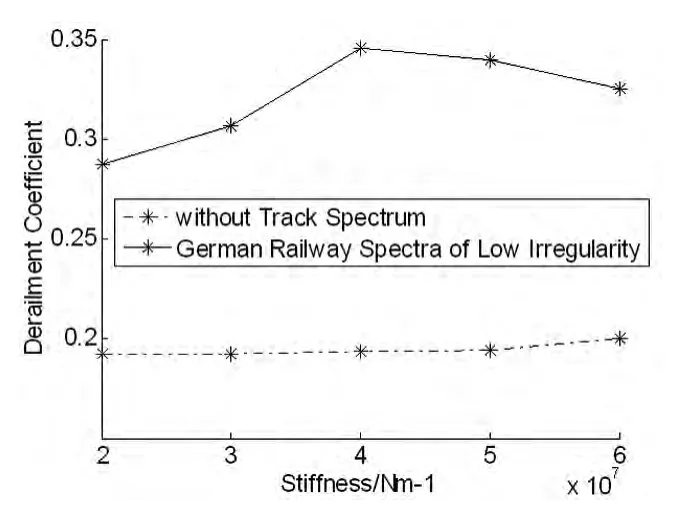
图8 脱轨系数Fig.8 Derailment coefficient

图9 车体垂向加速度Fig.9 Vertical carbody vibration accelerations

图10 轮轨垂向力Fig.10 Vertical wheel-rail force

从图6-图10可看出:

(1)轨下垂向刚度从2x107N/m变化到6x107N/m时，在无轨道激励下，脱轨系数增加4.09%.车辆动力学响应峰值出现在尖轨、心轨、尖轨与基本轨高度持平位置，轨道激励会在较大程度上影响到车辆动力学响应变化;

(2)车辆侧向通过道岔时，轨下垂向刚度增大，车辆垂向动力学响应随之增大，轨下刚度从2x107N/m变化到6x107N/m时，在无轨道激励下，车体最大垂向加速度增加50.12%，轮轨垂向力增加33.52%;

(3)车辆侧向过道岔时，轨下垂向刚度变化对车体最大横向加速度、轮轴横向力影响甚微.轨下垂向刚度发生变化时，在无轨道激励下，车体最大横向加速度增加4.09%，轮轴横向力增加5.01%.

由于仿真时轨下刚度和阻尼设置参考UIC60-760-1:15道岔，其曲线半径为760m，侧向通过速度为60km/h，其轨下垂向刚度和阻尼参数与18号可动心轨道岔有所区别.如有更详细资料，应针对轨下刚度和阻尼多层函数、轨下力学参数不均匀等情况做进一步分析.

4 结语

根据道岔实际结构，利用道岔区间左右钢轨变截面特征在多体动力学软件中建立60kg/m钢轨18号单开道岔模型及某型动车组拖车模型.经模型验证后，对车辆侧向和直向通过道岔进行动力学仿真，并对离散轨道变刚度工况进行动力学响应分析.主要工作与成果如下:

1)根据实际道岔截面形状和空间布置特征构造道岔模型，可仿真出道岔区间固有不平顺;

2)分别对车辆在曲线和道岔线路上进行仿真，仿真结果与现有文献中相关结果基本一致，确定本文中建立的车辆、LM踏面、道岔模型基本准确;

3)车辆在转辙器区和辙叉区有较大动力学响应;直向通过时，各项动力学响应好于侧向通过各值;道岔截面和轮轨几何接触关系是影响车辆—道岔耦合系统动力学响应特性的关键因素;

4)随着轨下垂向刚度增加，车辆垂向动力学响应随之增大.

1 全顺喜.高速道岔几何不平顺动力分析及其控制方法研究［博士学位论文］.成都:西南交通大学，2012(Quan S X.Study on dynamic analysis and control methods of the geometric irregularity in high-speed turnout［PhD thesis］.Chengdu:Southwest Jiaotong University，2012(in Chinese))

2 吴安伟.列车-变截面道岔动力学仿真分析［硕士学位论文］.成都:西南交通大学，2006(Wu A W.Analysis on the train-turnout system dynamics with variable cross-sections［Master Thesis］.Chengdu:Southwest Jiaotong University，2006(in Chinese))

3 Sun Y Q，Cole C，Boyd P.A numerical method using VAMPIRE modelling for prediction of turnout curve wheelrail wear.Wear，2011，271(1):482～491

4 中铁宝桥有限公司.铁路道岔参数手册.北京:中国铁道出版社，2009(China Railway Baoji Bridge Group CO.，LTD.Tie Lu Dao Cha Can Shu Shou Ce.Beijing:China Railway Publishing House，2009(in Chinese))

5 任尊松.车辆系统动力学.北京:中国铁道出版社，2007:46-54(Ren Z S.Vehicle system dynamics.Beijing:China Railway Publishing House，2007:46～54(in Chinese))

6 李刚.高速动车组道岔通过性能及影响因素分析［硕士学位论文］.成都:西南交通大学，2012(Li G.The performance of passing through the turnout of high-speed EMUSand the analysis of influencing factors［Master Thesis］.Chengdu:Southwest Jiaotong University，2012(in Chinese))

7 谷学思.不同踏面及轮径差对高速动车组曲线通过性能的影响［硕士学位论文］.北京:北京交通大学，2011(Gu SX.The influence of different wheel tread and roll radii difference on EMU curve negotiation［Master Thesis］.Beijing:Beijing Jiaotong University，2011(in Chinese))

8 李田，张继业，张卫华.横风下高速列车系统动力学的平衡状态法.动力学与控制学报，2013，11(3):264～269(Li T，Zhang J Y，Zhang W H.An equilibrium state method of high-speed train system dynamic in crosswind.Journal of Dynamicsand Control，2013，11(3):264～269(in Chinese))

9 Chalmers University of Technology.Summary of results from simulations and optimisation of switches.INNOTRACK Technical Report，February，2009:8～13

10 陈小平.高速道岔轨道刚度理论及应用研究［博士学位论文］.成都:西南交通大学，2008(Chen X P.Study in theory and application of track stiffness in high-speed turnouts［PhD thesis］.Chengdu:Southwest Jiaotong University，2008(in Chinese))