基于压电作动器/传感器的升力面颤振主动抑制*

岳承宇 王立峰 赵永辉

(南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016)

引言

颤振是严重的动气动弹性不稳定现象，当飞行器飞行速度超过颤振临界速度时，结构和空气动力相互作用，产生自激的振动，往往会引起灾难性的后果［1］.颤振主动抑制(AFS)技术是飞行器颤振研究的热门领域，相比于颤振被动抑制，其优点是适应性强、效果好、较少增加结构重量.基于主动气动弹性机翼(AAW)的设计理念［2］，通常做法是在机翼上布置多个控制面，通过主动控制翼面的变形，改变作用在机翼上的气动力，从而使系统趋于稳定［3-5］.这种方法的不足之处在于能量转换环节繁杂，附加部件多，可靠性不足［6］.

智能结构用于颤振主动抑制是一种具有广阔应用前景的设计理念，含有功能材料的结构除了具有承载能力，还有自我监测与作动功能［7］.众多功能材料中，压电材料能提供电能与机械能的直接转换，而且分布灵活，结构简单，响应迅速，从而备受关注.Lazarus等分别使用铝和石墨/环氧树脂为基板材料，将压电作动器分布于平直板的上下表面，对升力面的主动气动弹性控制问题进行了理论和实验研究，风洞试验结果表明颤振速度提高了11%［8］.在此基础上，Han等进一步对压电作动器进行了位置优化并应用鲁棒控制理论以提高控制效果［9］.国内由管德指导的小组进行了类似的工作，并且完成了风洞试验，成功利用压电作动器实施了升力面的颤振主动抑制［10］.

大部分利用压电材料进行颤振主动抑制的研究都是采用分布式压电作动器和传统的传感器组成的反馈控制系统，而较少使用压电传感器.实际上，压电传感器基于正压电效应，具有灵敏度高，频响范围大的特点.另一个特点是其在空间上呈连续分布，可以避免传统的传感器由于放置位置不当引起的个别模态观测不到的问题［11］.

已有研究通常使用单输入或较少输入的控制系统，文献［9］研究表明驱动力单一使得结构缺少扭转力的作用，从而颤振抑制效果受限.

本文使用多个压电作动器与传感器分布于整个机翼表面，作动器与传感器对称粘贴于上下两侧，并假设粘贴紧密.在已有的压电材料中，压电陶瓷(PZT)压电应变常数大，驱动力强，适合作为作动器，聚偏氟乙烯(PVDF)具有质轻、柔韧、灵敏的特点，适合作为传感器.故本文采用这两种不同的材料分别作为作动器与传感器.

复合材料层合板的有限元理论中，经典层合板理论(CLPT)适合薄板，一阶剪切变形板理论(FSDT)和高阶剪切变形板理论(HSDT)适合薄板和中厚板［12］，在考虑了模型的准确性和节省计算规模后，选择使用一阶剪切变形板理论来建立结构的机电耦合模型，并取其前4阶固有模态作为颤振的振型.本文对这种带有多个压电作动器与传感器的板式智能结构机翼进行了颤振主动抑制的研究.

1 有限元方程

1.1 位移场和电势场假设

图1为带有压电层的复合材料层合板示意图，压电铺层沿z轴极化，板一共有N层，上下两层分别为压电作动器层与传感器层，基板采用正交各向异性复合材料.根据一阶剪切变形板理论的假设，板上任意一点的位移为

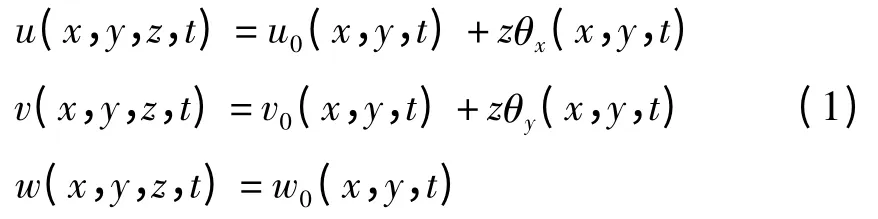
其中:u0、v0为板中面内的位移，w0为横向位移，θx、θy分别表示中面法线绕y、-x轴的转角.

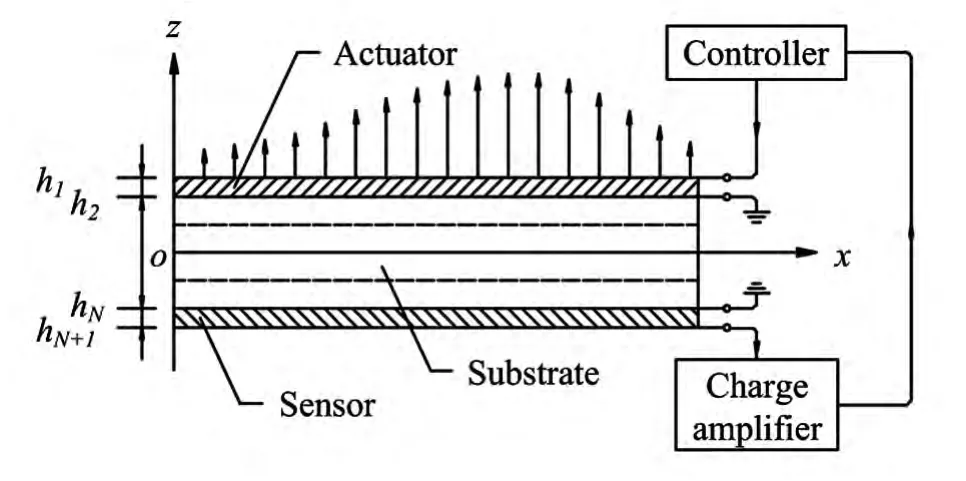
图1 压电层合板示意图Fig.1 Laminated piezoelectric plate configuration

将式(1)写为矩阵的形式为

其中:Δ为位移场向量，d为广义位移向量;Δ、d和矩阵Z的具体表达见附录A.

根据线弹性体的位移-应变关系，由位移场(1)导出的应变场表达式为

其中:εre为去掉了z方向正应变的各应变分量组成的向量为中面的面内正应变和切应变组成的向量，κ为中面的曲率和扭率组成的向量，γ0为横向切应变组成的向量.式中矩阵的具体表达式见附录B.

压电层与基板接触的那一面接地，在压电片的厚度很薄的情况下，可以假设电势φk(x，y，z，t)沿厚度的分布为线性的［12］(k=1，N)，写出压电作动器层和传感器层的电势场分布函数为

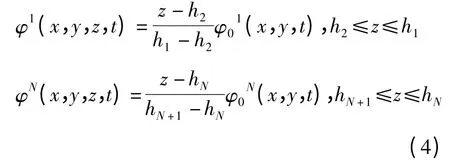
1.2 本构方程

压电材料的正压电效应和逆压电效应可以由如下的本构方程表达［13］

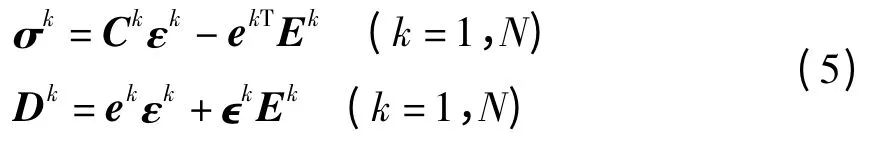
其中:Ck、ek、єk分别为材料的弹性常数矩阵、压电应力常数矩阵、介电常数矩阵，Ek、Dk为电场强度矢量和电位移矢量.

一阶剪切变形板理论假设板沿z方向无正应力，故压电材料的本构方程从一般完整的本构方程缩减为如下关系

其中:各矩阵的具体表达式见附录C.

基板部分为正交各向异性材料，其本构方程为

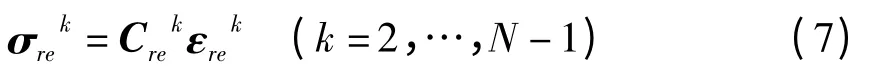
1.3 有限元插值

整个结构采用四节点四边形等参单元进行离散化，单元第i个节点的广义位移向量参照式(2)写为di(i=1，…，4)，而整个单元的节点广义位移向量写为

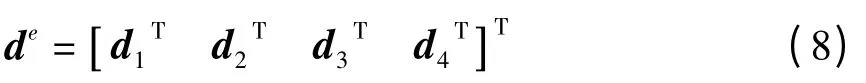
采用双线性插值函数对节点位移进行插值，广义位移向量可以由节点位移表示为

利用(9)式，(3)式中的广义应变可以写为

其中:应变矩阵Bε、Bκ、Bγ的具体表达式见附录D.

在解决剪切锁死的问题上，参考文献［15-16］的方法，另行假设横向剪切应变场替代原有的应变场γ0，使用单元采样点处的横向切应变值对整个单元的横向切应变进行独立插值，最后得到的替代横向切应变表示为

将(10)、(11)式一并写为

电场强度为电势的负梯度，即

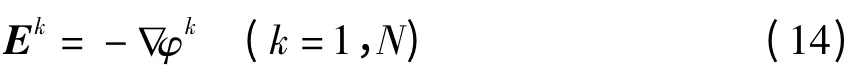
将(4)式、(13)式代入(14)式可得电场强度的离散表达为

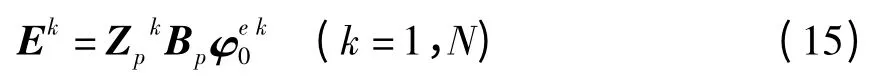
1.4 结构动力学方程

单元的总势能由弹性体应变能和压电层的电势能组成，表示为

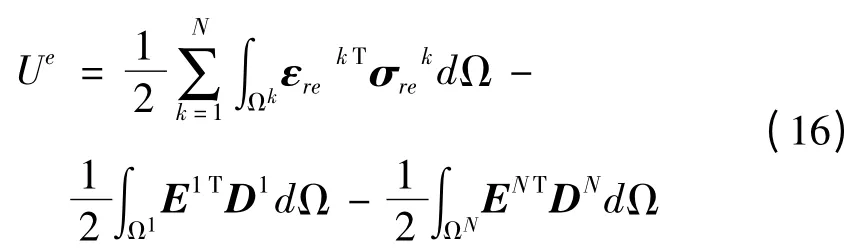
其中:Ωk为第k层的体积.

单元的动能为

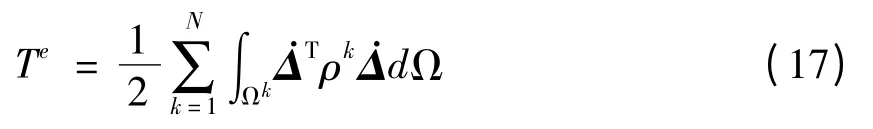
其中:ρk为第k层的质量密度.

单元的外力和外加电荷面密度做功为

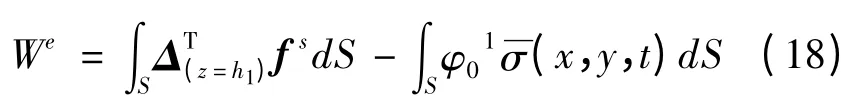
其中:S为单元的表面积，fs为单元上表面的面力向量，为施加在作动器上的外加电荷面密度.

结构的机电耦合动力学方程可以由Hamilton原理推出，Hamilton原理表示为

将(3)、(6)、(7)、(12)、(15)式代入(16)式，(2)、(9)式代入(17)式，(2)、(9)、(13)式代入(18)式，再将所得结果代入Hamilton方程(19)，得到单元的动力学方程为

其中:矩阵Me为单元质量矩阵，矩阵为单元结构刚度矩阵，矩阵、表示压电作动器和传感器的外加电载荷和单元节点电势差之间的对应关系，具有刚度属性，矩阵、表示作动器层、传感器层与基板之间的静态机电耦合效应.这些单元特性矩阵由结构的尺寸、压电层的分布以及材料的物理特性决定;计算时先沿z方向积分，再采用2×2的Gauss积分在自然坐标系下对单元表面进行积分［14］.为单元的等效外力向量表示施加在作动器层的电荷面密度产生的作用力.各矩阵的具体表达式见附录F.

实际操作中，作动器层的电势分布已知，通过控制电势分布，作动器对结构的作用可以写为等效外力的形式，式(20)可以写为

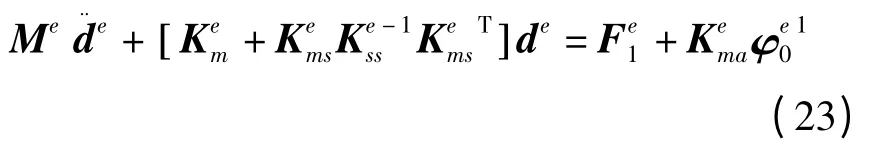
传感器层的单元节点电势差可由式(22)得到

对于没有压电层的单元，其运动方程可以由(23)式简化得到.经过组集得到结构的整体运动方程和传感器电压输出方程为

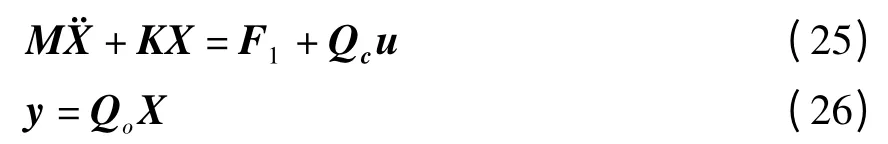
其中:X为结构整体位移自由度向量，u为作动电压输入向量，y为传感电压输出向量.

2 颤振特性分析

图2为机翼模型示意图，图中的网格为结构有限元网格划分，机翼为悬臂式的复合材料层合板结构，采用T300/976石墨/环氧树脂材料，厚度为3 mm，共4层，单层厚度为0.75 mm，铺层角度为［90/0/0/90］.机翼上分布15个压电区，片状的压电作动器和传感器对称粘贴于机翼上下表面，作动器材料采用PZT-5A，厚度为0.4 mm，传感器材料采用PVDF，厚度为0.1 mm.每个压电片的作动电压为独立变量，且在单个压电片上相同，传感器输出每个压电片中部的电压，计算时输出电压由单元节点电势差插值得到.

各材料的特性参数见附录G.

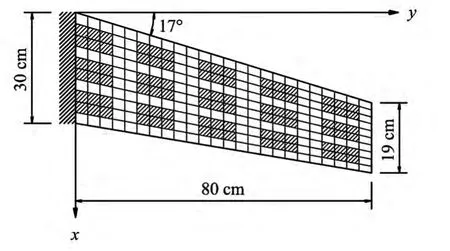
图2 机翼模型示意图Fig.2 Wing model configuration

对结构进行动力特性分析，即求解广义特征值问题

其中:Φ为固有振型矩阵，Λ为广义特征值组成的对角阵.

利用(25)式中的K、M矩阵对结构进行动力特性分析时，假设了电压输入u为0，即压电作动器上分布的电势差为0，这实际要求作动器闭路.计算机翼的前4阶固有模态如图3所示.

图3 机翼固有频率与固有振型Fig.3 Wing natural frequencies and mode shapes

采用偶极子网格法(DLM)计算频域亚音速非定常空气动力［17］，空气动力网格如图4所示，空气动力网格点与结构有限元网格点的连接采用无限板样条(IPS)方法［18］.(25)式中的F1写为与结构有关的频域气动力形式

其中:qd为动压，Qgg为广义空气动力矩阵，是减缩频率和马赫数M∞的函数.

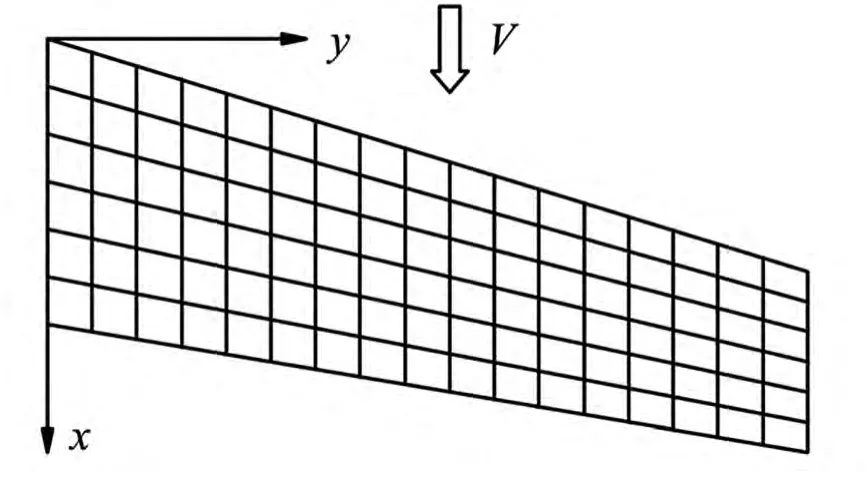
图4 升力面上的空气动力网格Fig.4 Aerodynamic grids on the lifting surface

引入模态坐标变换

其中:Φ只取结构的前4阶振型，q为模态坐标向量.

得到模态坐标下的气动弹性方程和传感器电压输出方程为

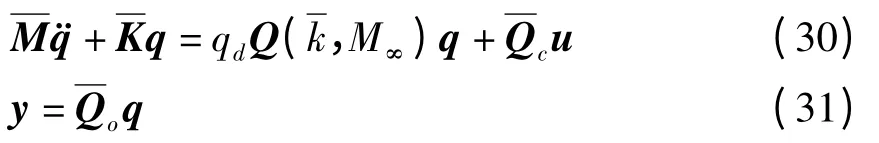
采用V-g法对未控系统进行颤振分析［18］，取海平面处大气密度ρa=1.225kg/m3，并假设空气为不可压缩流(M∞=0)，得到颤振V-g和V-f图如图5所示.从图中可以看出机翼的颤振速度为51.74 m/s，颤振频率为19.90 Hz.

3 时域状态空间方程

在设计颤振主动抑制的控制律时，需要用到时域的空气动力，(30)式中由偶极子网格法计算出的广义空气动力矩阵Q，M∞)是在机翼做简谐运动的条件下得到的，属于频域气动力.为了得到时域气动力，通常的做法是利用若干离散频率点处的广义空气动力矩阵，将空气动力矩阵Q在Laplace域用有理函数拟合表达，再通过引入空气动力状态变量，将整个方程转换到时域，最后得到被控系统时域下的状态空间方程.

本文采用Roger近似法拟合空气动力矩阵［18］，矩阵Q，M∞)在Laplace域中近似表示为

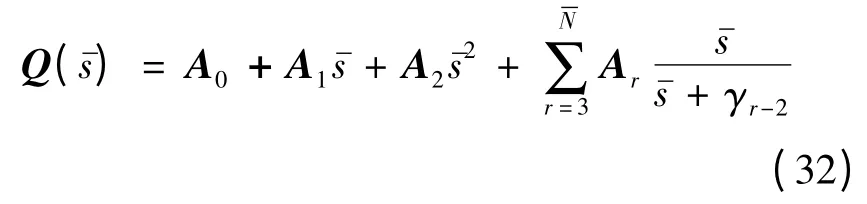
其中:A0，…，为待定系数矩阵，γr-2为空气动力滞后项=sbR/V，s为拉氏变量，bR为参考半弦长，V为来流速度.各待定系数矩阵根据已知频率点处的空气动力矩阵Q，M∞)求得.

引入空气动力状态变量

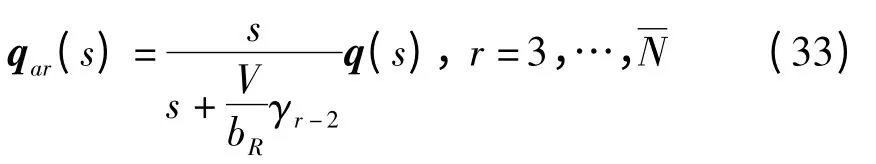
由(33)式可得空气动力状态变量自身满足的时域微分方程为

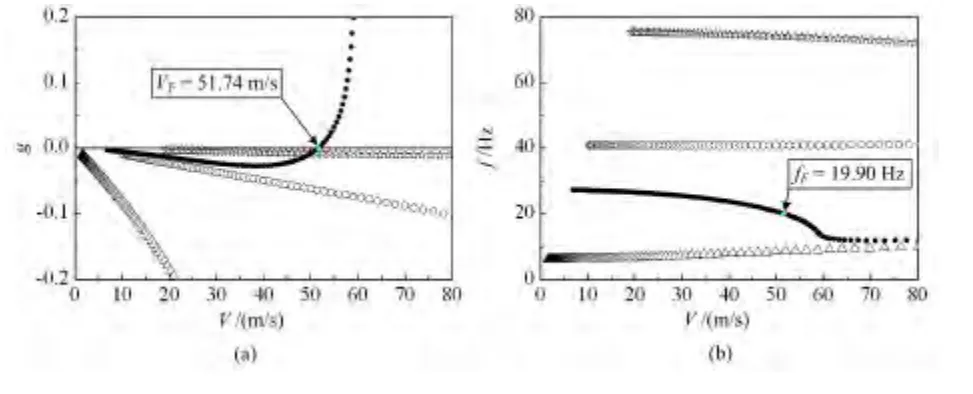
图5 颤振V-g和V-f图Fig.5 FlutterV-g and V-f plots

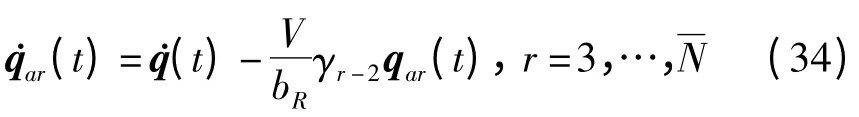
利用式(32)将(30)式右边第一项在Laplace域近似表示，引入空气动力状态变量后再作Laplace逆变换，最终(30)式可以写为

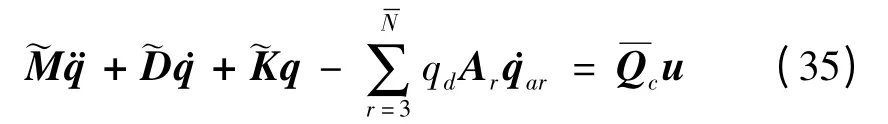
其中:Acon、Bcon、Ccon分别为系统矩阵、输入矩阵与输出矩阵，其具体表达式见附录H.

4 控制律设计与仿真分析

最优控制理论中［19］，线性定常系统的输出调节器问题表述为寻找最优控制律

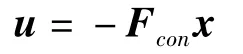
使得如下二次型性能指标达到极小

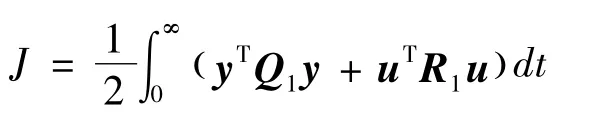
其中:Q1、R1为对应输入和输出的权系数矩阵，为了使问题简化，均取为正定对角阵.权矩阵的取值由经验给定，合适的权矩阵使系统尽快镇定的同时，输入电压应保持在压电材料可以承受的范围.

增益反馈矩阵Fcon由下式求得

其中:P1为如下Riccati方程的解

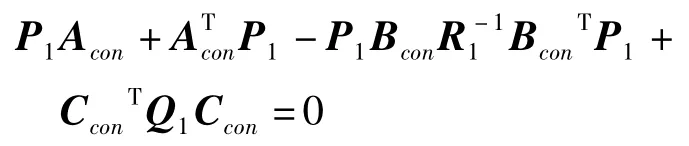
针对本文的气动弹性系统，状态变量x中包含结构的模态坐标及其对时间的一阶导数，另外还有引入的空气动力状态变量，状态变量x实际上无法直接测得.LQG控制增加了最优滤波器设计过程，通过系统的输入u和输出y，可得出状态变量x的最优估计值，表示为

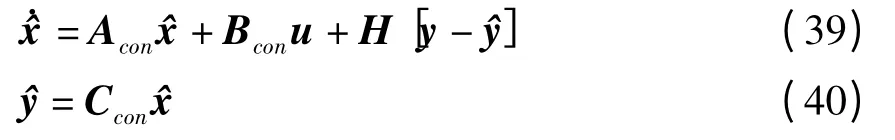
根据Kalman滤波理论，若系统存在噪声，对状态变量和输出变量测量过程中Gauss白噪声的协方差矩阵分别为Q2和R2，滤波器增益矩阵H为

其中:P2为如下Riccati方程的解

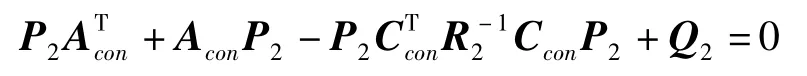
LQG控制律表示为

包括了控制器的闭环系统结构由图6所示，系统的状态方程为

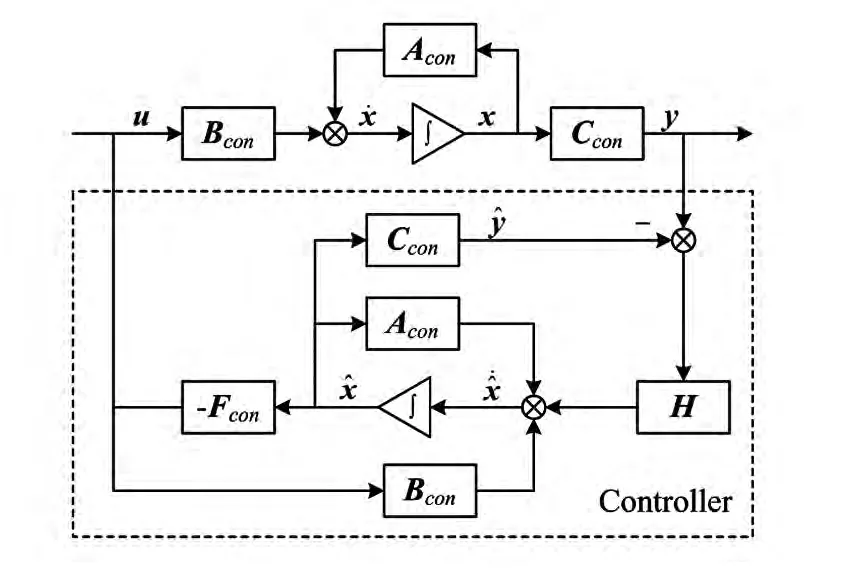
图6 LQG控制器结构Fig.6 Block diagram of LQG controller

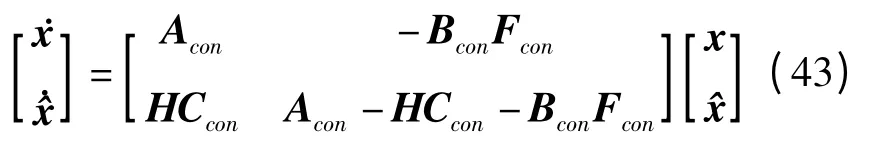
为了精确拟合气动力，本文取4个空气动力滞后项，分别为γ1=0.34，γ2=0.89，γ3=2.56，γ4=13.46，此时系统矩阵Acon为24阶.对开环、闭环系统进行稳定性分析，随着来流速度的增加，系统特征根轨迹如图7所示，图中删去了零频率附近无意义模态的特征根.

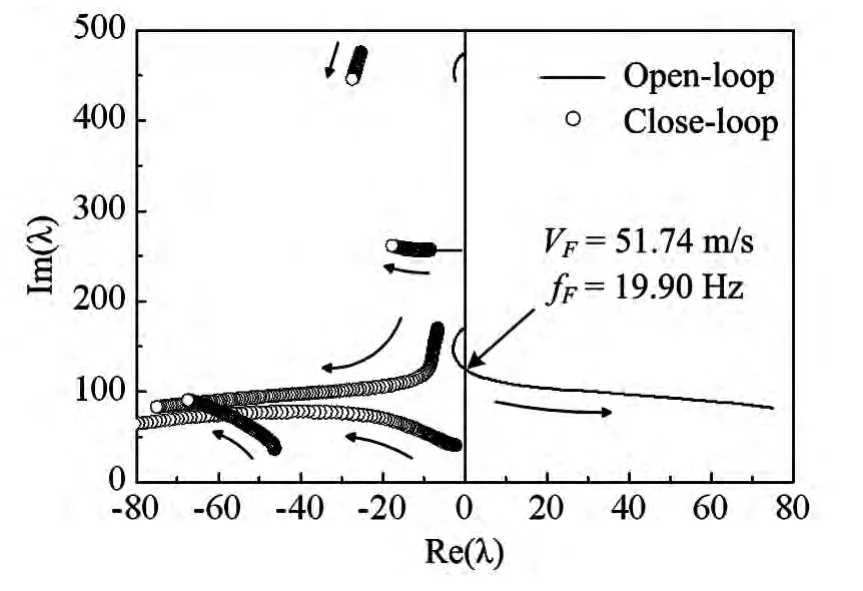
图7 随着来流速度增加开闭环系统的根轨迹Fig.7 Root locus of open-loop and close-loop system with increasing incoming flow velocity

未控系统在来流速度达到51.74m/s时开始出现正实部的特征根，即发生了颤振，其结果与上文V-g法颤振分析得到的结果相同.闭环系统的特征根全部在复平面的左半平面，表明受控系统是稳定的.在流速较大时(V=100m/s)，系统仍保持稳定，这个结果是在未考虑压电作动器的最大承载电压的情况下得到的，实际上在流速较大时，轻微的扰动也需要作动器提供较大的驱动力才能使系统镇定，作动电压有可能超出了压电材料所能承受的极限，此种情况本文未作考虑.另一方面，本文使用了15个压电作动器分布在整个机翼表面，对机翼前数阶模态的联合颤振有较全面的控制能力，在更多模态参与下的颤振抑制效果还有待研究.

对系统进行动响应仿真计算，采用Runge-Kutta法求解系统的动响应，设定来流速度V=54m/s，在t=0.5s时施加控制，结果如图8所示.

图中位移响应为翼梢后缘点的横向位移时间历程，可以看到系统在初始扰动下发散运动，施加控制后大约在t=1s时系统趋于镇定.图中给出的控制电压是翼根处的三块压电作动器的控制电压，一般情况下所有作动器的控制电压最大值不超过第一块作动器的最大控制电压，LQG控制律的算法是让总的控制能量尽可能的小，第一块压电作动器在控制过程中起到了较大作用.

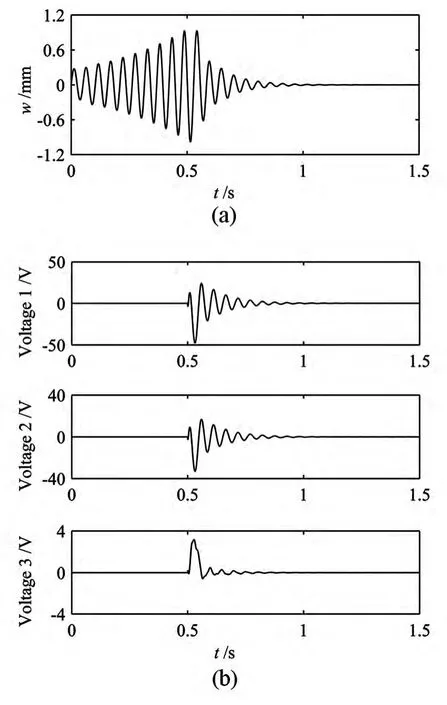
图8 系统的时间历程(V=54m/s)Fig.8 Time histories of the system at V=54m/s

5 结论

本文研究了一个带有分布式压电作动器与传感器的复合材料板结构机翼的升力面颤振的主动抑制问题.多对压电作动器与传感器对称粘贴在机翼上下表面，作动器和传感器采用不同的压电材料，传感器输出由于结构变形产生的电压，作动器主动输入控制电压使作动器对结构产生作用力.通过主动控制律的实施，升力面颤振被较好地抑制，证明了本文颤振主动抑制方法的有效性.

本文较详细地推导了复合材料压电层合板的有限元方程，建模方法不局限于本文中上下两面粘贴有压电片的板结构模型，还可以推广到压电片嵌于复合材料板之中的结构，压电层数也可以是多层.

今后可研究作动器和传感器的位置优化以提高控制效率，研究考虑模型不确定性的鲁棒控制或自适应控制以接近工程实际.

1 Librescu L，Marzocca P.Advances in the linear/nonlinear control of aeroelastic structural systems.Acta Mechanica，2005，178(3-4):147～186

2 吴志刚，杨超.主动气动弹性机翼的颤振主动抑制与阵风减缓研究.机械强度，2003，25(1):32～35(Wu Z G，Yang C.Investigation on active flutter suppression and gust alleviation for an active aeroelastic wing.Journal of Mechanical Strength，2003，25(1):32～35(in Chinese))

3 Borglund D，Kuttenkeuler J.Active wing flutter suppression using a trailing edge flap.Journal of Fluids and Structures，2002，16(3):271～294

4 Zhao Y H.Flutter suppression of a high aspect-ratio wing with multiple control surfaces.Journal of Sound and Vibration，2009，324(3):490～513

5 杨仕福，王琪，赵永辉等.大展弦比机翼μ控制.动力学与控制学报，2011，9(1):79～85(Yang SF，Wang Q，Zhao Y H，et al.μControl of a high-aspect-ratio wing using multiple actuators.Journal of Dynamics and Control，2011，9(1):79～85(in Chinese))

6 任勇生，刘立厚，韩景龙等.飞行器非线性气动弹性和颤振主动控制研究进展.力学季刊，2003，24(4):534～540(Ren Y S，Liu L H，Han JL，et al.Advance in nonlinear aeroelasticity study and active flutter suppression of aircraft.Chinese Quarterly of Mechanics，2003，24(4):534～540(in Chinese))

7 陈勇，熊克，王鑫伟等.飞行器智能结构系统研究进展与关键问题.航空学报，2004，25(1):21～25(Chen Y，Xiong K，Wang X W，et al.Progress and challenges in aeronautical smart structure systems.Acta Aeronautica et Astronautica Sinica，2004，25(1):21～25(in Chinese))

8 Lazarus K B，Crawley E F，Lin C Y.Multivariable active lifting surface control using strain actuation:analytical and experimental results.Journal of Aircraft，1997，34(3):313～321

9 Han JH，Tani J，Qiu J.Active flutter suppression of a lifting surface using piezoelectric actuation and modern control theory.Journal of Sound and Vibration，2006，291(3):706～722

10 陈伟民，管德，李敏等.采用分布式压电驱动器升力面的颤振主动抑制.力学学报，2002，34(5):756～763(Chen W M，Guan D，Li M，et al.Flutter suppression using distributed piezoelectric actuators.Acta Mechanica Sinica，2002，34(5):756～763(in Chinese))

11 Tzou H S，Tseng CI.Distributed piezoelectric sensor/actuator design for dynamic measurement/control of distributed parameter systems:a piezoelectric finite element approach.Journal of Sound and Vibration，1990，138(1):17～34

12 Samanta B，Ray M C，Bhattacharyya R.Finite element model for active control of intelligent structures.AIAA Journal，1996，34(9):1885～1893

13 Benjeddou A，DeüJ F，Letombe S.Free vibrations of simply-supported piezoelectric adaptive plates:an exact sandwich formulation.Thin-Walled Structures，2002，40(7-8):573～593

14 王勖成.有限单元法.北京:清华大学出版社，2003:111～112，145～147(Wang X C.Finite element method.Beijing:Tsinghua University Press，2003:111～112，145～147(in Chinese))

15 Hinton E，Huang H C.A family of quadrilateral Mindlin plate elements with substitute shear strain fields.Computers＆structures，1986，23(3):409～431

16 Nayak A K，Moy SSJ，Shenoi R A.Free vibration analysis of composite sandwich plates based on Reddy＇s higher-order theory.Composites Part B:Engineering，2002，33(7):505～519

17 Albano E，Rodden WP.A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows.AIAA Journal，1969，7(2):279～285

18 赵永辉.气动弹性力学与控制.北京:科学出版社，2007:246～250，278～280，310～315(Zhao Y H.Aeroelasticity and control.Beijing:Science Press，2007:246～250，278～280，310～315(in Chinese))

19 顾仲权，马扣根，陈卫东.振动主动控制.北京:国防工业出版社，1997:68～71(Gu Z Q，Ma K G，Chen W D.Active vibration control.Beijing:National Defense Industry Press，1997:68～71(in Chinese))

20 Ha SK，Keilers C，Chang FK.Finite element analysis of composite structures containing distributed piezoceramic sensors and actuators.AIAAJournal，1992，30(3):772～780

21 Xu K，Noor A K，Tang Y Y.Three-dimensional solutions for free vibrations of initially-stressed thermoelectroelastic multilayered plates.Computer Methods in Applied Mechanics and Engineering，1997，141(1):125～139

22 Shen S，Kuang Z B.An active control model of laminated piezothermoelastic plate.International Journal of Solids and Structures，1999，36(13):1925～1947

23 Mitchell JA，Reddy JN.A refined hybrid plate theory for composite laminates with piezoelectric laminae.International Journal of Solids and Structures，1995，32(16):2345～2367