Spar平台月池水晃动的等效力学模型及模型参数研究*

刘利琴 满金双 周斌 张若瑜

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300072)(2.中海油能源发展采油服务公司，塘沽 300457)

引言

Spar平台是深海油气田开发的重要平台形式之一，目前对Spar平台的研究主要集中在主体波浪载荷与水动力特性、平台动力响应计算、垂荡与纵摇运动不稳定性分析、系泊系统与立管系统的模拟以及涡激振动等方面［1-2］.有关Spar平台月池内部流体的运动及平台与月池流体之间的耦合运动研究较少.Spar平台的中央井自下而上贯穿整个主体，其内按照一定的方式布置立管和其它重要钻井设施，构成Spar平台的月池.若采用顶张紧器张紧立管，则月池内海水的质量与平台整体质量量级相当，月池内流体的运动与平台主体运动耦合显著［3］.

Spar平台月池内流体运动与储液容器或液舱中流体流动有一定的相似之处，存在两类固有振荡形式，即沿深度方向的“活塞(Piston)”振动和流体液面的左右“晃荡(sloshing)”运动.人们基于理论分析及数值模拟的方研究了储液容器及液舱中流体运动动力学模型及流体与结构的耦合运动.Molin应用模态分解法将船舶舱内液体运动处理为一系列弹簧-质量-阻尼系统，建立了横浪中驳船与舱液耦合运动的半解析模型，研究了舱内液体晃动与船舶的耦合运动［4］.Faltinsen考虑非线性自由表面条件，基于建立在Bateman-Luke变分原理基础之上的变分方法，创立了多维模态方法，研究了任意运动情形下二维和三维矩形容器中各种不同充液深度、不同激励幅值和不同激励频率下的共振晃动问题［5-7］.包光伟等采用有限元数值计算方法研究了液体的三维晃动特征问题，得到了任意刚性容器内液体三维晃动的固有频率和模态［8］.李青等研究了非轴对称贮箱液体晃动的等效力学模型，确定了液体晃动的等效力学参数并计算出了液体晃动产生的作用力与力矩［9］.

本文基于线性势流理论，借鉴储液容器晃荡问题的研究方法［9］建立Spar平台月池流体晃动的等效力学模型，确定其模型参数，为进一步研究Spar平台-月池流体的耦合运动建模及耦合系统动力学特性奠定基础.

1 基于势流理论建立月池内流体运动方程

图1所示为平台月池结构示意图，选取OOXYZ为惯性坐标系，Oxyz为固定在平台上的本体坐标系.其中Ω为月池流体的内部区域，Σ为月池流体的自由液面，S为平台硬舱与月池流体的交界区域.

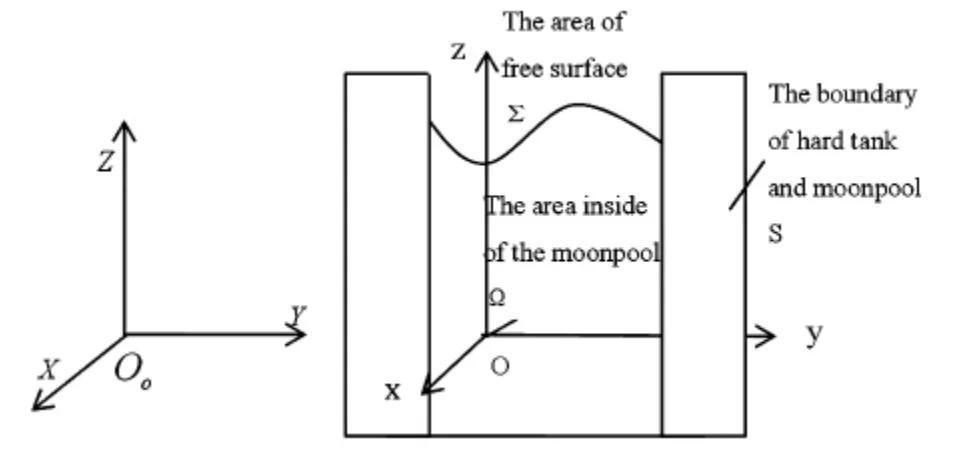
图1 Spar平台月池结构及坐标系示意图Fig.1 Moonpool structure andcoordinate system of Spar platform

当平台作三维运动时，相对于本体坐标系O点矢径为r的流体质点的速度v可以写成

其中vs，ωs分别为平台相对于惯性坐标系下的运动速度以及转动角速度，u为月池内流体质点相对于平台的运动速度.

将平台月池底部处理为全封闭，假定月池内流体为不可压缩、无旋、无粘性的理想流体，且平台运动为小幅运动，应用线性势流理论，建立月池流体的运动方程为:

其中，Φ为速度势，n为交界区域的外法向单位矢量.采用Stokes-Zhukovskiy势函数将速度势写为:

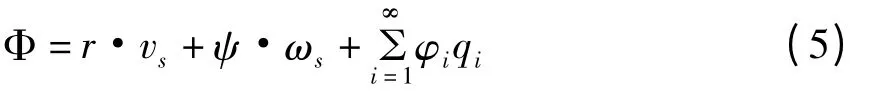
其中，ψ为Stokes-Zhukovskiy势函数，φi为第i阶流体晃动模态函数，qi为第i阶流体晃动广义坐标，则式(2)～(4)可以化简为以下边值问题:

其中，ωi为第i阶模态特征频率，根据势函数ψ的定义，有:

根据伯努利方程计算月池内流体流场动压力为:

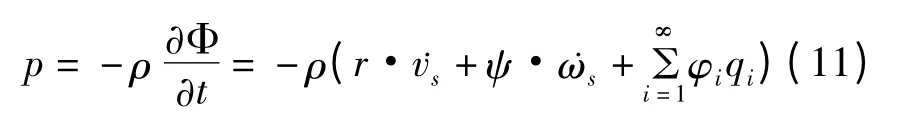
对上式的压力积分，得到月池内流体对平台的作用力、作用力矩及动能分别为:

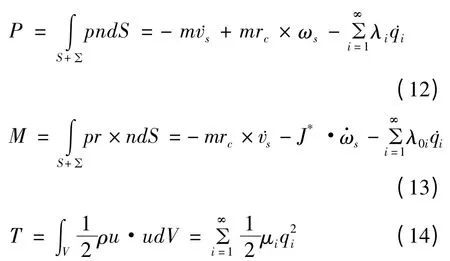
其中，m为月池内流体的总质量，rc为月池内流体质心矢径，λi和λ0i分别为流体第i阶晃荡对平台的作用力系数以及作用力矩系数，J*为流体等效刚体相对O点的惯性张量.定义μi为广义晃动质量［10］，有:

2 月池内流体晃动等效力学模型建立

对于底部封闭的贮液容器，容器运动时，容器内靠近自由液面附近的流体发生明显晃动，其它流体随容器一起做刚体运动，这部分流体可等效为随容器运动的质量块.容器内晃动流体的动力学特性可用单摆模型或弹簧-质量模型来描述［11］.本文研究的平台月池底部为半开口，对于吃水很大的深海平台，底部开口对月池内流体晃动的固有振动特性影响不大［12］.基于此，本文采用等效力学模型理论研究深海平台半开口月池内流体的动力学特性，为进一步研究平台-月池流体的耦合运动奠定基础.以下采用单摆等效月池内流体的晃荡，如图2所示.

构建等效力学模型的条件如下［11］:(1)等效力学模型的质量及惯量与原流体质量及惯量保持一致;(2)保持重心位置不变;(3)特征频率及流体产生的作用力与力矩相等;(4)等效力学模型的动能与原系统的动能相同.假设不同模态间不耦合，根据以上等效条件，可以求得等效力学模型中的固定质量块及各阶单摆的质量、摆长和挂点位置等力学参数.

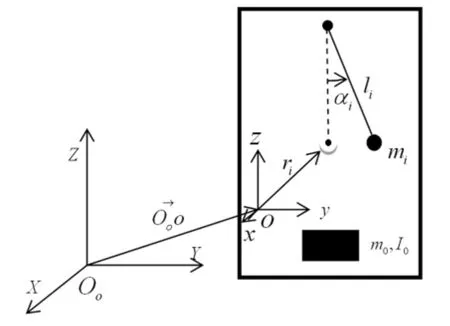
图2 单摆模型示意图Fig.2 Pendulum model

根据刚体动理论写出单摆系统的动能为:

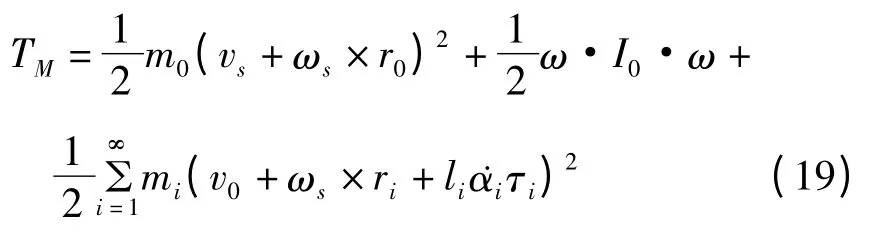
根据拉格朗日方程，等效单摆系统对平台主体产生的作用力及力矩分别为:

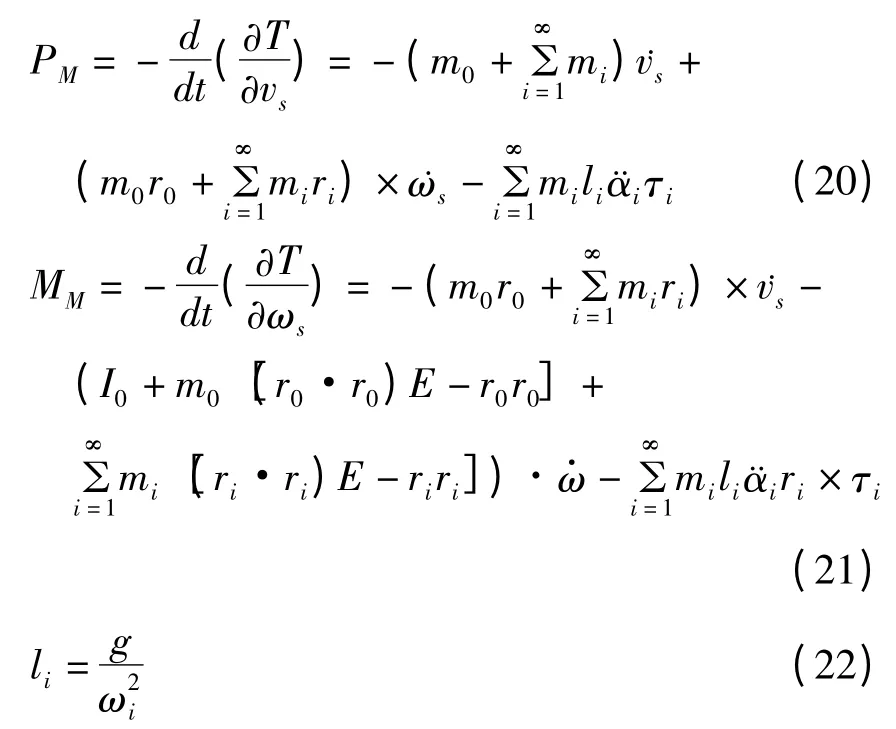
其中，m0、r0、I0分别为固定质量块的质量、相对于O点的矢径及对质心的转动惯量;mi、ri分别为第i阶单摆质量以及平衡位置相对于O点的矢径;li、αi、τi分别为第i阶单摆的摆长、摆角以及单摆晃动方向的单位矢量;ωi为由势流理论计算得到的流体晃动的第i阶晃动固有频率.相应的等效条件为:

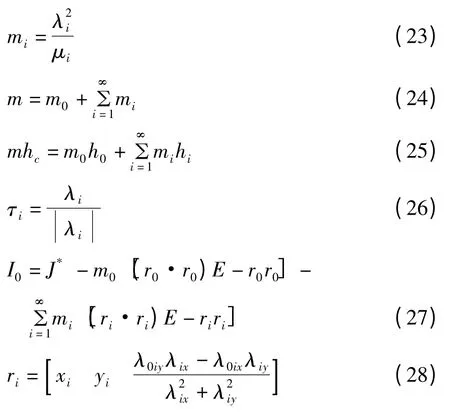
上式中，λix、λiy和λ0ix、λ0iy、λ0iz分别为λi、λ0i的分量;hc为月池内流体的重心位置，为已知量;h0和hi分别为等效力学模型中质量块及单摆的重心位置.xi、yi并不唯一，满足如下关系式:

由质心rc=(xc，yc，zc)到公式(29)所示直线的距离最短原则求得［9］:

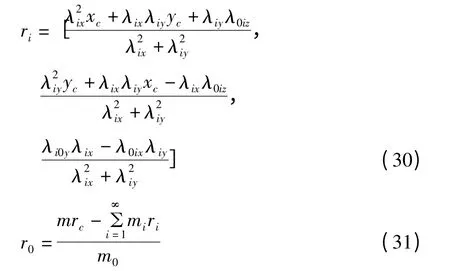
可以看出，等效参数由Stokes-Zhukovskiy势函数ψ、第i阶流体晃动模态函数φi以及特征频率ωi决定，因此想要获得等效参数，需对势函数、模态函数以及特征频率进行求解.

3 有限元方法数值求解

对于截面为规则的矩形或圆形容器，可由势流方程直接求得其内部流体晃动的势函数ψ、模态函数φi及特征频率ωi的解析表达式，从而获得等效单摆模型参数的解析解，详见文献［11］.本文采用有限元方法数值求解势流方程，求解流体晃动的势函数、模态函数及特征频率的数值解，并确定等效力学模型参数，该数值方法能够用于不规则的结构形式.

对方程(6)～(10)采用伽辽金变分法，有:

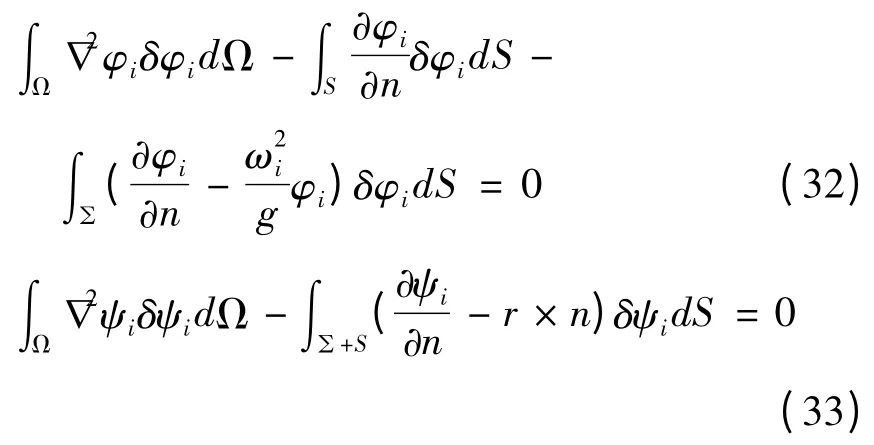
将月池流体进行网格划分、离散，即将每个单元势函数以及模态函数离散成和带入到式(30)和式(31)中.本文计算中，在自由液面以及边界面处采用三角形单元，其它采用四面体单元进行划分，并应用格林公式进行化简，得到如下求解的基本方程:

对式(30)和式(31)进行求解，得到相应的势函数ψ、第i阶流体晃动模态函数φi以及特征频率ωi，从而可确定等效力学模型参数.

4 算例

平台参数如表1所示［13］.先用ANSYS软件进行前处理，建立月池内流体模型并划分网格;之后，将结点编号坐标以及单元结点信息输出到MATLAB进行数值运算.月池内流体采用四面体单元进行网格划分，六个边界面上采用三角形单元划分，通过APDL参数化编程命令将整体的四面体单元信息按照单元编号、单元结点编号进行输出;将结点信息按照结点编号、结点空间坐标进行输出;将月池流体模型六个边界面的三角形单元信息按照单元编号、单元结点编号进行输出.

运用Matlab编辑有限元程序，应用Ansys输出的单元信息进行计算，得到月池内流体运动的固有频率及其对应的等效单摆模型参数.本文计算的月池截面形状为正方形，为验证有限元计算过程的正确性，将数值结果与按照文献［11］中得到的解析解进行对比，结果如表2～表4所示.

表1 平台参数Table 1 The parameters of the Spar platform

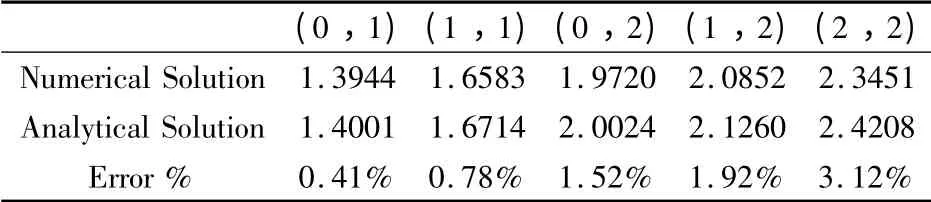
表2 月池内流体晃动固有频率(rad/s)Table 2 Natural sloshing frequencies of the water inside the moonpool(rad/s)

表3 第一阶等效单摆模型参数Table 3 The model parameters of the first orderequivalent pendulum

表4 等效质量块参数Table 4 The parameters of the equivalent mass

可以看出，计算误差随着等效模型阶次的增加而增大，这与单元划分的数目以及单元类型有关.增加单元的数目并选择高精度的单元类型有助于提高计算精度.数值解法与解析解法对比的误差很小，证明了有限元数值程序的正确性.

当月池底部开口时，随着平台的垂荡运动，月池内外流体产生交换，月池内液面高度也随之变化.下面运用上述有限元方法建立月池内不同液面高度时流体晃动的等效力学模型参数库.选取不同的自由液面高度，计算月池内流体晃动等效单摆模型第一阶单摆参数，结果如表5所示.

表5表明，随着月池内液面高度的增加，第一阶单摆模型的质量及悬挂点高度增加，但单摆的摆长随平台吃水的增加变化不大.

表5 不同吃水时的第一阶等效单摆模型参数Table 5 The model parameters of the first orderequivalent pendulum with different draft

5 结语

本文建立了Spar平台月池内流体晃动的动力学模型，推导了月池内流体晃动的等效单摆模型，通过两个模型的等效关系确定了等效力学模型参数.采用ANSYS软件作为模型建立及网格划分的前处理软件;运用Galerkin有限元方法求解月池内流体晃动的固有频率、模态函数以及势函数离散解;应用Matlab软件编制了月池流体晃动的计算程序.数值模拟结果与解析解进行了比较，表明了有限元数值计算方法的正确性.另外，建立了不同月池液面高度的等效力学模型参数库，为进一步研究平台-月池内流体的耦合运动奠定了基础.

1 唐友刚.海洋工程结构动力学.天津:天津大学出版社，2008:6～10(Tang Y G.Structure dynamics of ocean engineering.Tianjin:Tianjin University Press，2008:6～10(in Chinese))

2 王颖，杨建民，肖龙飞.Spar平台与刚性立管及浮力罐耦合动力研究综述.海洋工程，2008，26(2):140～146/154(Wang Y，Yang J M，Xiao L F.Review on the study of coupled analysis of Spar platform，TTR and buoyancy can.The Ocean Engineering，2008，26(2):140～146/154(in Chinese))

3 Gupta H，Blevins R，Banon H.Effect of moonpool hydrodynamics on spar heave.In:Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering.New York:American Society of Mechanical Engineers，2008:275～282

4 Molin B，Remy F，Rigaud S，et al.LNG FPSO＇s:frequency domain，coupled analysis of support and liquid cargo motions.In:Proceedings 10th IMAM Conference.Crete，2002

5 Faltinsen O M，Rognebakke O F，Lukovsky I A，et al.Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth.Journal of Fluid Mechanics，2000，407:201～234

6 Faltinsen O M，Rognebakke O F，Timokha A N.Resonant three-dimensional nonlinear sloshing in asquare-base basin.Journal of Fluid Mechanics，2003，487:1～42.

7 Faltinsen O M，Firoozkoohi R，Timokha A N.Analytical modeling of liquid sloshing in a two-dimensional rectangular tank with a slat screen.Journal of Engineering Mathemmatics，2011，70:93～109

8 包光伟，王政伟.液体三维晃动特征问题的有限元数值计算方法.力学季刊，2003，20(2):185～190(Bao G W，Wang Z W.Finite element method for eigen problem of liquid 3D sloshing.Chinese Quarterly of Mechanics，2003，24(2):185～190(in Chinese))

9 李青.充液挠性系统动力学分析及在航天工程中的应用研究［博士学位论文］.北京:清华大学，2010(Li Q.Dynamic analysis of liquid-filled flexible systems and its application studies on aerospace engineering［PhD Thesis］.Beijing:Tsinghua University，2010(in Chinese))

10 岳宝增，杨旦旦，吴文军.微重力环境下刚液耦合系统液体晃动混沌现象研究.动力学与控制学报，2013，11(4):306～313(Yue B Z，Yang D D，Wu W J.Nonliner coupled dynamics of liquid-filled cylinedrical container in microgravity.2013，11(4):306～313(in Chinese))

11 Ibrahim R A.Liquid sloshing dynamics:Theory and applications.Cambridge University Press，New York，2005.

12 黄磊.开口式月池水动力特性研究［博士学位论文］.天津:天津大学，2014(Huang L.Study on hydrodynamic characteristics of moonpool with bottom open［PhD Thesis］.Tianjin:Tianjin University，2014(in Chinese))

13 Petter A B.Dynamic response analysis of a truss spar in waves.Newcastle，University of Newcastle，2000