移动简谐力激励非线性无限长地基梁稳态响应*
时伉丽 丁虎† 陈立群,2 储德林
(1.上海大学上海市应用数学和力学研究所,上海 200072)(2.上海大学力学系,上海 200444)(3.陆军军官学院应用物理研究所,合肥 230031)
引言
近一个世纪来,铁路、公路运输已发展成为我国乃至世界主要的交通形式之一.车辆在运行过程中对路面、路基造成破坏,而路面的破坏又反过来影响到车辆的运行,对行车的舒适性、安全性能造成威胁.所以研究路面在车辆作用下的振动对于交通运输方面有很重要的现实意义.通过移动载荷激励下地基梁的响应模拟铁路、公路动力学的研究工作引起多方关照[1-5].
对于地基梁动力学的研究,学者们主要关注于线性地基模型.例如,Sun等研究分布式激励的地基梁的稳态响应[6].时伉丽等的研究表明,地基对梁的剪切力不能忽略[7].随着移动载荷激励的线性地基梁动力学的研究深入,学者们发现,实际路基是高度非线性的,因此非线性是一个不可忽略的因素.非线性地基梁的响应问题逐渐得到关注.由于移动载荷在数学处理上的特殊性,研究非线性地基梁响应的方法比较单一.龙述尧[8]和Ding等[9]运用模态截断法,通过有限长地基梁模型研究了移动集中恒力作用下的地基梁响应,发现地基的非线性弹性影响显著.Wu和Thompson[10]用有限元的方法研究了非线性地基对轮、轨相互作用的影响.为了丰富非线性地基梁的研究手段,Hryniewicz和Koziol借助无线长地基梁模型,通过小波方法研究了非线性地基梁对移动集中力的响应[11].Ding等通过无限长非线性地基梁,比较摄动方法和Adomian分解法对移动集中力响应的近似解析解[12].研究表明,无限长地基梁模型能够用于研究移动载荷作用下的非线性地基梁响应问题的研究.Kargarnovin通过无限长地基梁模型,运用摄动方法研究了移动简谐力作用下非线性地基梁的响应[13].研究发现,移动简谐力的频率对地基梁的响应有着显著影响.
本文综合考虑了地基中的非线性弹性以及地基对梁的剪切力的影响,研究了移动简谐力作用下4参数非线性黏弹性地基梁的稳态响应.扩展非线性地基梁的研究方法,应用Adomian多项式分解方法,处理移动简谐力作用下立方非线性地基梁响应.研究地基中的非线性弹性和剪切模量,以及移动简谐力的频率以及移动速度的影响.
1 模型建立
车与路相互作用是个复杂的动力学问题,为了考察移动车辆激发的路面动态响应,本文将路面模型化为无限长的Euler-Bernoulli梁,考虑地基中的非线性以及黏弹性因素,并计入路基的剪切变形影响,将车辆简化成一个移动的集中简谐力.其力学模型如图1所示.图中的u为梁的横向变形,x为沿着路面水平轴线方向的空间坐标,t为时间,F0为移动简谐力的恒定幅值,v为移动简谐力沿路面移动的定常速度,ω为移动简谐力的振动频率.
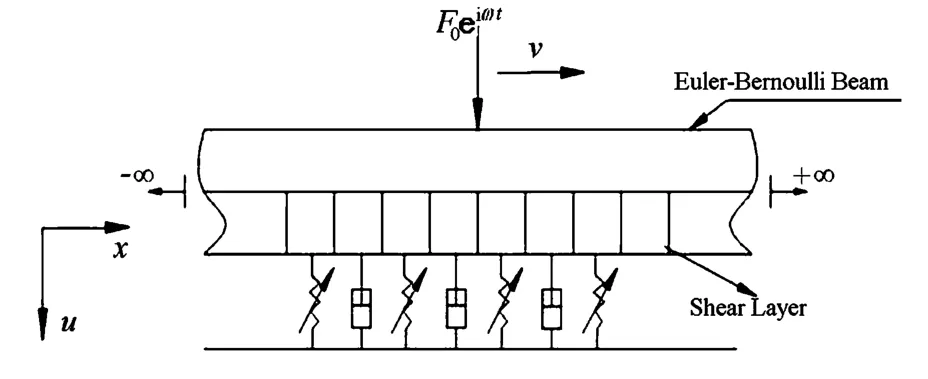
图1 简谐激励下粘弹性Euler-Bernoulli梁模型Fig.1 A model for an Euler-Bernoulli beam on a nonlinear viscoelastic foundation under a moving harmonic load
基于Euler-Bernoulli梁理论的假设,移动集中简谐力作用下非线性黏弹性地基梁动态响应的控制方程可以写成如下形式[9]

其中EI为梁的刚度,ρ为梁的密度,A为梁的横截面积,变量x前面的逗号表示对空间坐标x求偏导数,t前面的逗号表示对时间坐标t求偏导数,P为地基对路面的作用力,假设地基为4参数立方非线性黏弹性Pasternak模型[13]
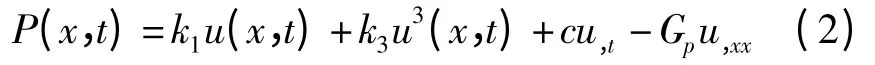
其中k1为地基的线性弹性系数,k3为地基的非线性弹性系数,c为地基的阻尼系数,Gp为地基的剪切系数.式(1)中的δ(x-vt)为迪利克雷函数,定义如下
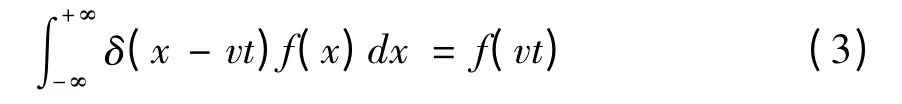
其中f(x)为任意函数.
2 Adomian多项式求解
Adomian方法是一种半解析半数值的迭代方法,已经成功应用于求解非线性方程[14].Adomian方法是将非线性项展开为Adomian多项式,运用递归方法计算方程的近似解.该方法应用广泛,能够解决弱线性问题,强线性问题,边界值问题,随机问题等.该方法的主要优点是在保持高精度的同时缩减计算量.下面将通过运用Adomian方法处理移动简谐力作用下的无限长非线性路基上Euler-Bernoulli梁的稳态响应问题.
假设控制方程(1)式的稳态响应u(x,t)可以写成如下无穷个多项式的和的形式

将上式带入式(1)中,得到
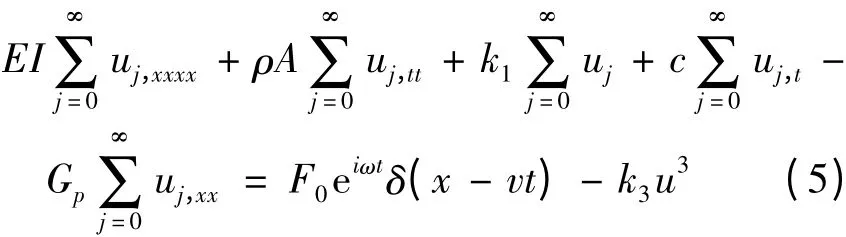
将非线性项g(u)=u3写成无穷展开的形式

其中序列Aj为关于u0,u1,u2,…的Adomian多项式.将式(6)代入式(5),并写成递归的形式,当j=0时,有
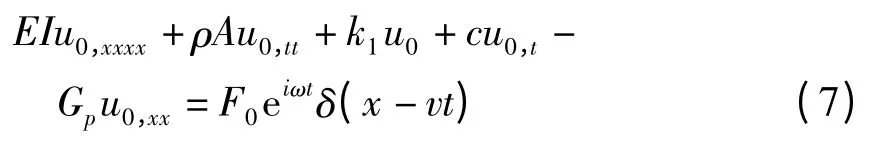
当j≥1时,有
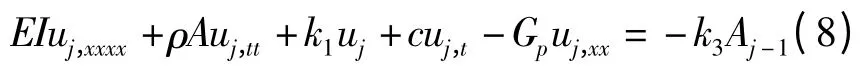
Adomian方法将非线性项分解为如下多项式
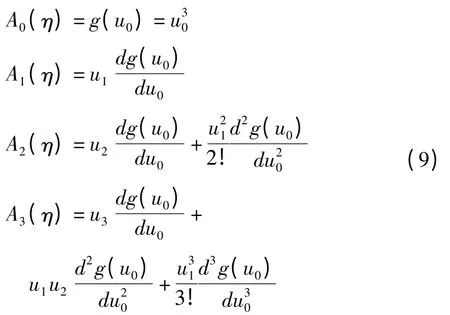
因此,这里的Aj可以写为

考虑到道路模型为无限长,而且移动载荷沿着x正方向以常速v运动,因此,进行如下坐标变换

假设式(7)解的形式为

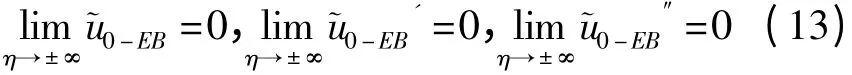
其中的撇号代表对η求导数.应用链式法则[13-14],将u0(x,t)的偏导数展开为
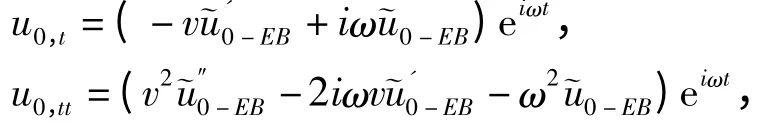

将式(14)代入式(8),并应用傅里叶变换可得
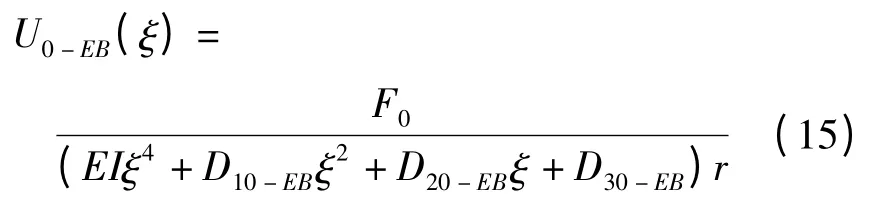
其中U0-EB(ξ)为格林函数,另外

对式(15)应用傅里叶逆变换,可得
根据留数定理可知,函数的积分可以写成被积函数的留数和的形式.因此可求得在复数域上的封闭解:
当η≥0时,
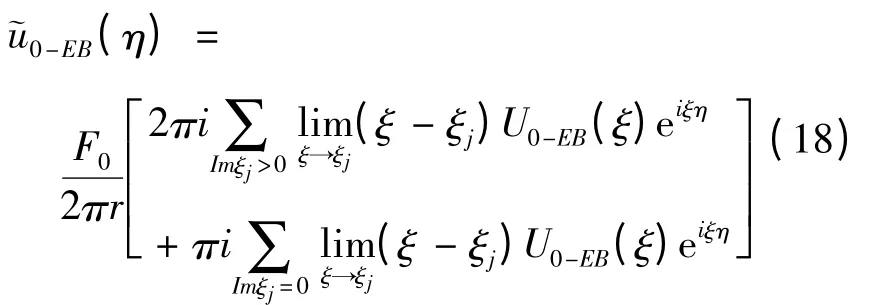
其中ξj为U0-EB(ξ)在复平面上半平面的极点;
当η≤0时,

其中ξj为U0-EB(ξ)在复平面下半平面的极点.式(17)存在高阶极点时,封闭解的形式为如下形式:
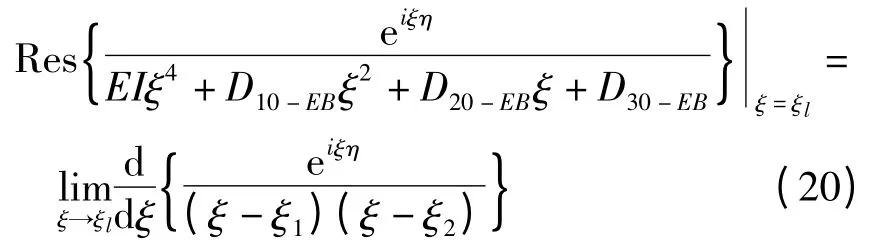
其中ξl为U0-EB(ξ)的二阶极点,ξ1,ξ2为U0-EB(ξ)的一阶极点.
通过以上推导,已经给出j=0时的封闭解.接下来考虑j=1和2时的解.将式(9)展开为
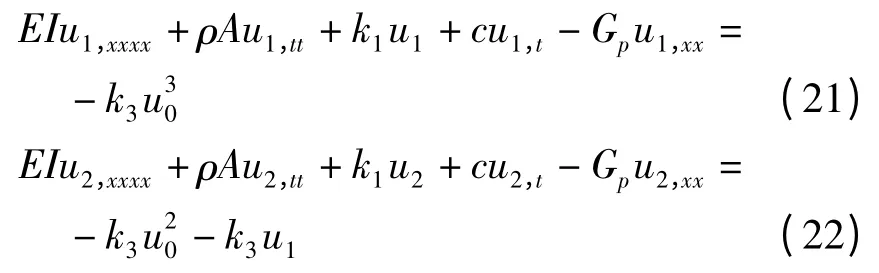
通过相似的过程,对于式(21)和(22),引入格林函数并应用卷积定理,可以求解系统的响应

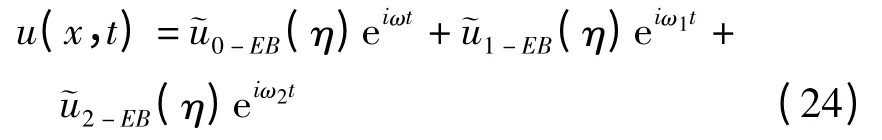
综合以上推导,结合式(17)、(23)和(24),再给定各个物理参数值,即可以计算地基梁的动态响应.
3 算例分析
接下来通过计算软件计算式(24),引入算例计算地基梁的近似稳态响应,并分析不同参数对地基梁动态响应的影响.采用UIC60欧洲高速铁轨的路面、路基以及载荷参数[9,15],如表1所示.
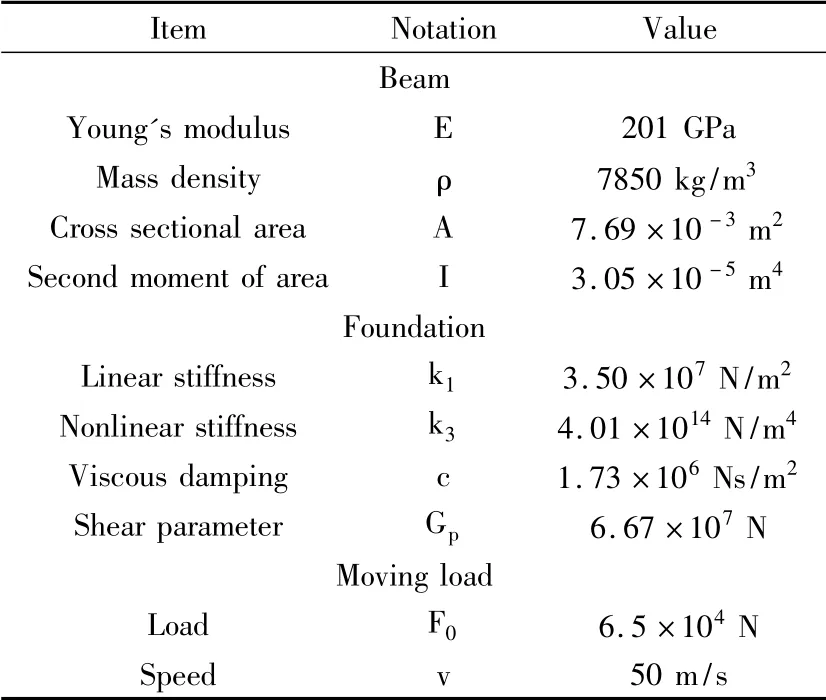
表1 地基梁以及载荷的参数值Table 1 Properties of the beam,foundation and load Table 1 Example
图2给出了移动简谐力的频率变化以及速度变化对梁稳态响应的影响.图2(a)给出了4组不同的移动速度下、零时刻梁坐标原点处的稳态响应随简谐力频率的变化.由图2(a)可知,在低频区,零时刻梁坐标原点处的稳态响应随着移动简谐力的频率以及速度的增大而减小,稳态响应在频率ω=0时达到最大.另外,当简谐力的频率较大时,稳态响应受简谐力的频率和速度的影响较小.由图2(a)还可以看出,当简谐力的速度较大时,当简谐力的频率变化对梁稳态响应的影响不如简谐力的速度较小时的影响大.图2(b)、图2(c)和图2(d)分别在取不同移动简谐力速度时,比较了频率对梁时间响应历程的影响.观察图2(b)、图2(c)和图2(d)可知,当移动简谐力速度恒定时,对应于较高的移动简谐力频率,梁动态响应的变化呈震荡状,而且最大的横向变形量较小.纵观图2,在移动简谐力下的非线性Euler-Bernoulli地基梁的响应中,移动简谐力的频率和速度对梁横向变形的影响不能忽略.

图2 频率变化、速度变化对梁稳态响应的影响Fig.2 Effects of the frequency and the speed of moving harmonic load on the deflection of the beam
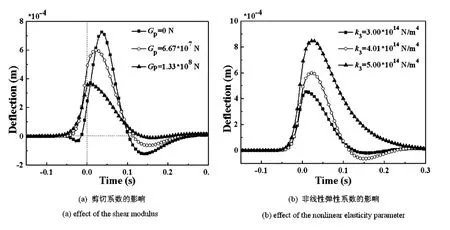
图3 移动简谐力下地基的剪切系数、非线性弹性系数的变化对梁横向变形的影响Fig.3 Effects of the shear modulus and the nonlinear elasticity parameter of foundations on the deflection of the beams
图3给出了地基的剪切系数和非线性弹性系数对移动简谐力下地基梁横向变形的影响.其中,外激励的频率为ω=5 Hz.从图3(a)可以看出,随着地基剪切系数的增大,梁的最大稳态响应及其迟延都逐渐减小.从图3(b)则显示随着地基非线性弹性系数的增大,梁的最大稳态响应及其迟延都逐渐增大.当地基的剪切力与非线性弹性系数较小时,在t=0.1~0.2s时出现了负挠度,且这种负挠度随着地基剪切力和非线性弹性系数的增加而逐渐不明显.
4 结论
研究移动集中简谐力激励的无限长道路响应问题.通过将路面模型化为Euler-Bernoulli弹性梁,将路基模型化为弹性支撑地基,并计入地基弹性的立方非线性项以及地基的黏性和剪切系数,建立非线性地基上Euler-Bernoulli梁横向振动响应的控制方程.应用Adomian分解方法处理控制方程中的非线性项,再通过Fourier变换与Fourier逆变换得到控制方程解的近似解析表达式,最后,对解的积分表达式应用留数定理得到复数域上的近似解析解.通过数值算例分析表明,地基的非线性弹性系数和剪切系数的变化对地基梁的稳态响应影响明显,并且发现当移动简谐力的速度比较低时,移动简谐力的频率对地基梁稳态响应的影响最为显著.
1 Kenney J.Steady state vibrations of beam on elastic subgrade for moving loads.ASME Journal of Applied Mechanics,1954,21(4):359~64
2 杨端生,黄炎,潘军.双参数弹性地基上板的自由振动.动力学与控制学报,2004,2(1):92~96(Yang D S,Huang Y,Pan J.Free vibration of plates on the bi-parameter elastic foundation.Journal of Dynamics and Control,2004,2(1):92~96(in Chinese))
3 张望喜,易伟建,谢小安,陈友坤.非均匀地基上自由梁的刚体模态分析.动力学与控制学报,2007,5(4):355~360(Zhang W X,Yi WJ,Xie X A,Chen Y K.Analysis on rigid modal of free beam on inhomogeneity foundation.Journal of Dynamics and Control,2007,5(4):355~360(in Chinese))
4 李皓玉,杨绍普,李韶华.车、路的相互作用下沥青路面动力学特性分析.振动与冲击,2009,28(4):86~92(Li H Y,Yang SP,Li SH.Dynamical analysis of an asphalt pavement due to vehicle-road interaction.Journal of Vibration and Shock,2009,28(4):86~92(in Chinese))
5 马建军,王连华,赵跃宇.弹性地基有限长梁的动力学建模.中国科学:物理学 力学 天文学,2013,43(6):765~771(Ma J J,Wang L H,Zhao Y Y.Dynamic modeling of the finite-length beam on the elastic foundation.Science China:A Physics,Mechanics&Astronomy,2013,43(6):765~771(in Chinese))
6 Sun L,Gu W,Luo,F.Steady state response of multilayered viscoelastic media under a moving dynamic distributed load.ASME Journal of Applied Mechanics,2009,75:041001
7 时伉丽,丁虎,陈立群,储德林.移动载荷黏弹性Pasternak地基梁动力学响应.上海大学学报(自然科学版),2012,18(6):617~621(Shi K L,Ding H,Chen L Q,Chu D L.Dynamic response of pasternak beams on viscoelastic foundations to moving load.Journal of Shanghai University(Natural Science Edition),2012,18(6):617~621(in Chinese))
8 龙述尧.用无网格局部Petrov-Galerkin法分析非线性地基梁.力学季刊,2002,23(4):547~551(Long SY.An analysis of beam on nonlinear foundation by meshless local Petrov-Galerkin method. Chinese Quarterly Mechanics,2002,23(4):547~551(in Chinese))
9 Ding H,Chen L Q,Yang S P.Convergence of Galerkin truncation for dynamic response of finite beams on nonlinear foundations under a moving load.Journal of Sound and Vibration,2012,331(10):2426~2442
10 Wu T X,Thompson D J.The effects of track non-linearity on wheel/rail impact.Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2004,218:1~12
11 Kargarnovin M H,Younesian D,Thompson D J,Jones C JC.Response of beams on nonlinear viscoelastic foundations to harmonic moving loads.Computers and Structures,2005,83:1865~1877
12 Hryniewicz Z,Koziol P.Wavelet-based solution for vibrations of beam on nonlinear viscoelastic foundation due to moving load.Journal of Theoretical and Applied Mechanics,2013,51:215~224
13 Ding H,Shi K L,Chen L Q,Yang S P.Dynamic response of infinite Timoshenko beams on nonlinear viscoelastic foundations to a moving load.Nonlinear Dynamics,2013,73(1-2):285~298
14 Adomian G.A new approach to nonlinear partial differential equations.Journal of Mathematical Analysis and Applications,1984,102:420~434
15 Dahlberg T.Dynamic interaction between train and nonlinear railway track model.In:Proceedings of the Fifth European Conference on Structural Dynamics,Munich,Germany,2002(2):1155~1160

