一类耦合抽象非线性梁方程组的整体解*
郝晓荣 张建文
(太原理工大学数学学院,太原 030024)
引言
2008年,Pedro Pablo Durand Lazo[1]运用Galerkin方法证明了以下抽象方程
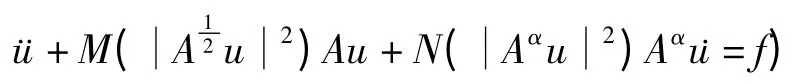
整体解的存在性,其中0<α≤1,M(s),N(s)∈C([0,+∞);R),且对∀s≥0,m0,n0>0,有M(s)≥m0,N(s)≥n0.
2010年,李润民,张建文[2]等研究了以下一类抽象非线性梁方程
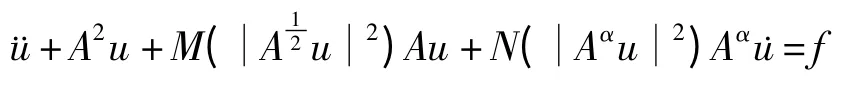
在初始条件u(x,0)=u0,˙u(x,0)=u1,x∈Ω下整体弱解的存在性问题,其中Ω=(0,l),0<α≤1.
2011年,张建文,丁霞霞[3]等研究了以下抽象耦合非线性方程组
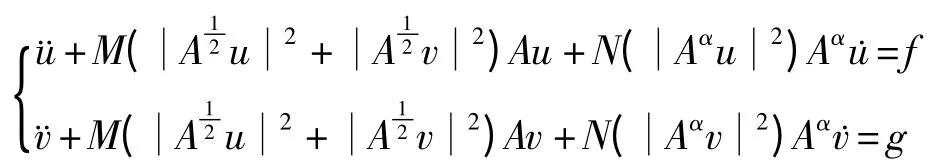
在一定的初始条件下整体弱解的存在性问题,其中Ω=(0,l),l>0,0<α≤1.
在本文中,我们将研究如下的一类抽象耦合非线性梁方程组

在初始条件
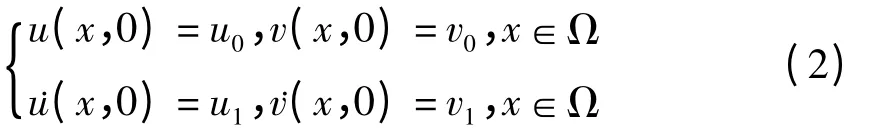
下整体弱解的存在性问题,其中Ω=(0,l),l>0,0<α≤1,0<β≤1,函数M(.),N(.)的定义同文[1]
1 预备知识
设{V,((.,.))}和{H,(.,.)}均为实的Hilber t空间,V连续且稠密地嵌入到H中,算子A是由三重结构(V,H,((.,.)))定义的,则A是定义在Hilbert空间H上的正定自共轭算子,A的特征值{λj}满足0<λ1<λ2<…<λn<…及λn→+∞(n→+∞),它所对应的特征值向量{ωj(x)}j∈N+.
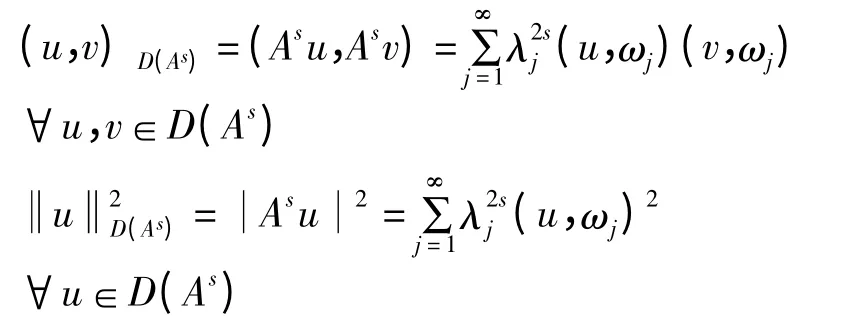
特别,s=0,时,记H=D(A0);并且记
引理1[4](Gronwall不等式)设f∈L∞(0,T),k≥0,c0为常数,若对一切t∈[0,T]下式成立:
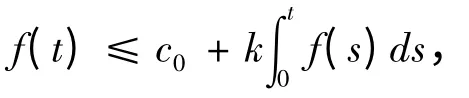
则
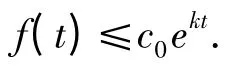
引理2[4]设X,Y为Hilbert空间或可分的Banach空间,其对偶空间为X',Y',设Y连续且稠密地嵌入到X中,若uμ→u在L∞(0,T;X')中弱*收敛;且˙uμ→χ在L∞(0,T;Y')中弱*收敛;则χ=˙u在L(0,T;Y')中成立.
2 弱解的存在性
定理 设0<α≤1,0<β≤1,M(.),N(.)∈C([0,+∞);R),存在m0,n0>0,且对∀z≥0,有M(z)≥m0,N(z)≥n0,A是定义在Hilbert空间H上的正定自共轭算子,若
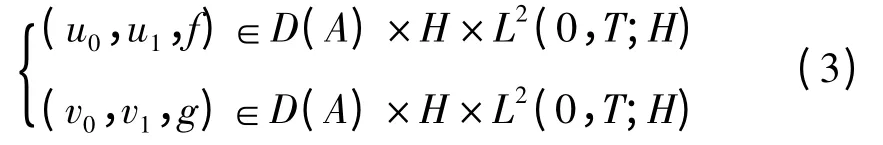
则问题(1)和(2)存在一个弱解(u,v)=(u(x,t),v(x,t)),对∀φ∈V,在D'(0,T)中,满足方程

及初始条件
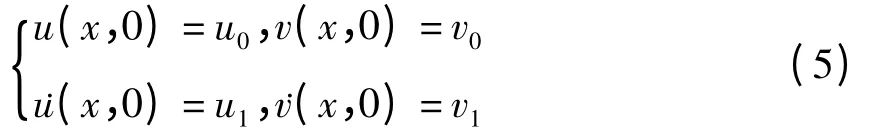
且
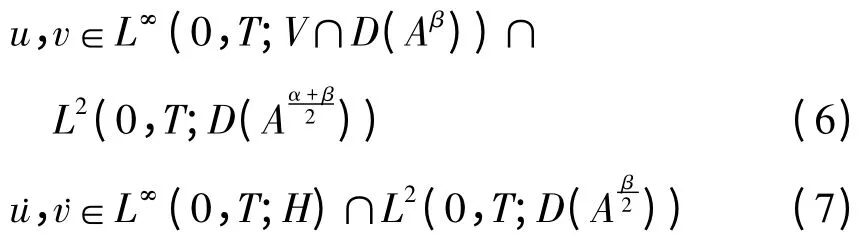
证明:记Vm为A的前m个特征向量ω1,ω2,…,ωm所张成的子空间,显然Vm⊂D(A),构造初值问题(1),(2)的近似解序列{um(x,t),vm(x,t)}如下:
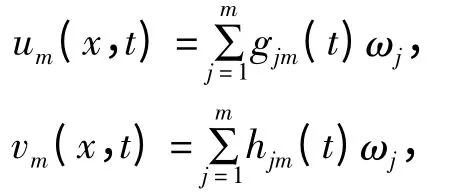
使得∀φ∈Vm满足以下方程
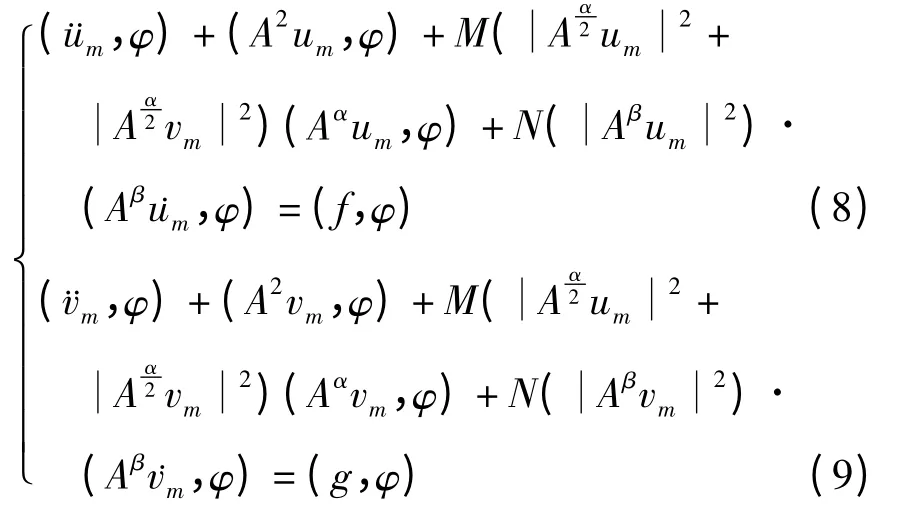
在(8),(9)中分别取φ=ωj(j=1,2…,m),得
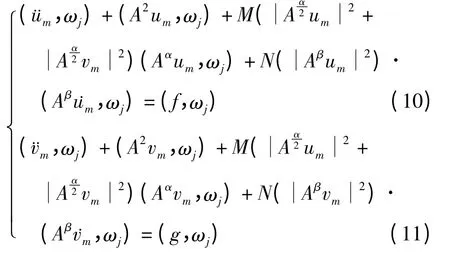
及初始条件

在D(A)中强收敛;
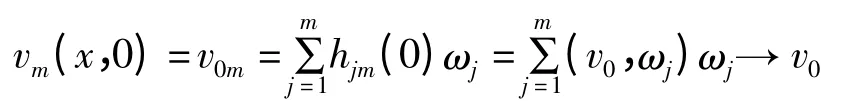
在D(A)中强收敛;
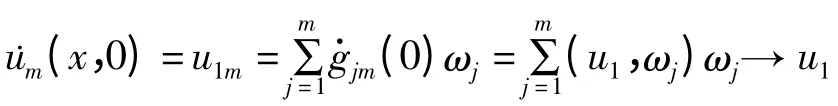
在H中强收敛;
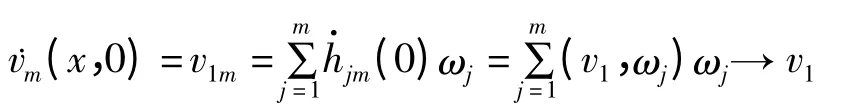
在H中强收敛.
由常微分方程理论知,存在tj>0,使得方程组(10)和(11)在相应的初始条件下,在[0,T](T=上存在解{gjm(t),hjm(t)},从而可得近似解{um(x,t),vm(x,t)}.

即
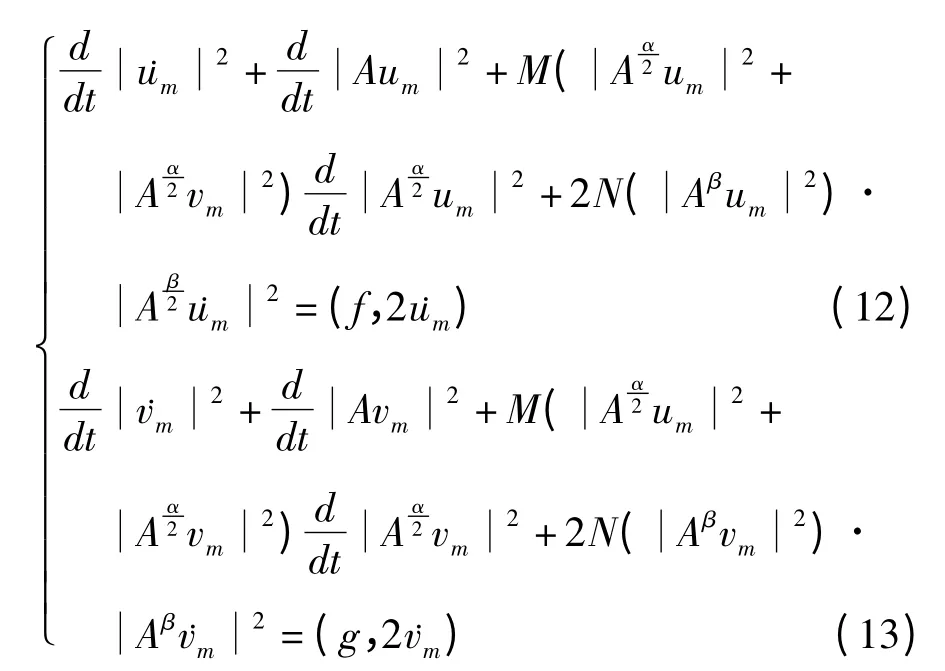
对(12),(13)两式分别从0到t积分并相加得
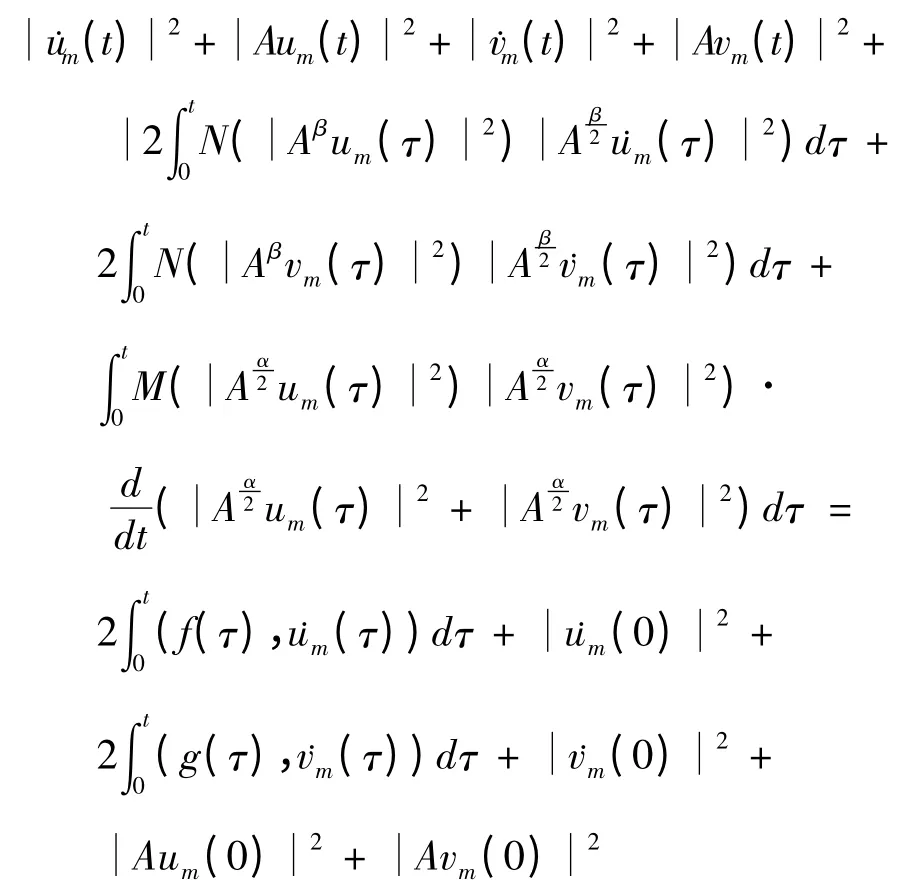
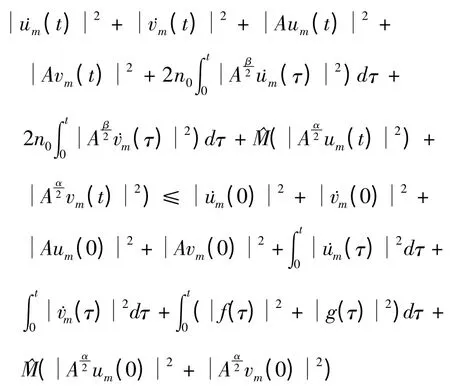
类似于文献[1]由Gronwall不等式可得
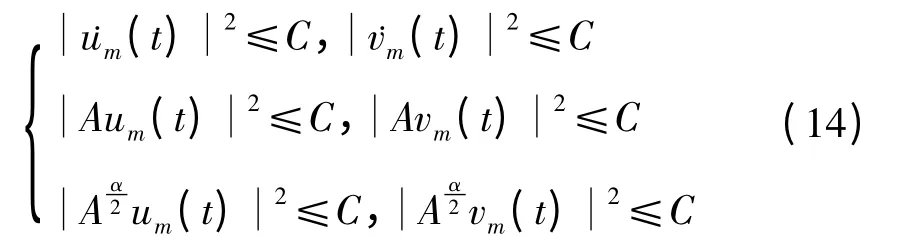
且容易得出
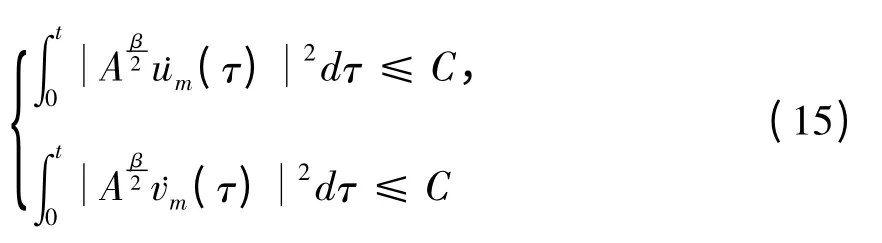
其中C表示与m,t无关的正常数,且在不同的地方表示不同的值.
(8),(9)两式中分别取φ=Aβum(t),φ=Aβvm(t),可得

将(16),(17)分别从0到t积分,并将两式相加得
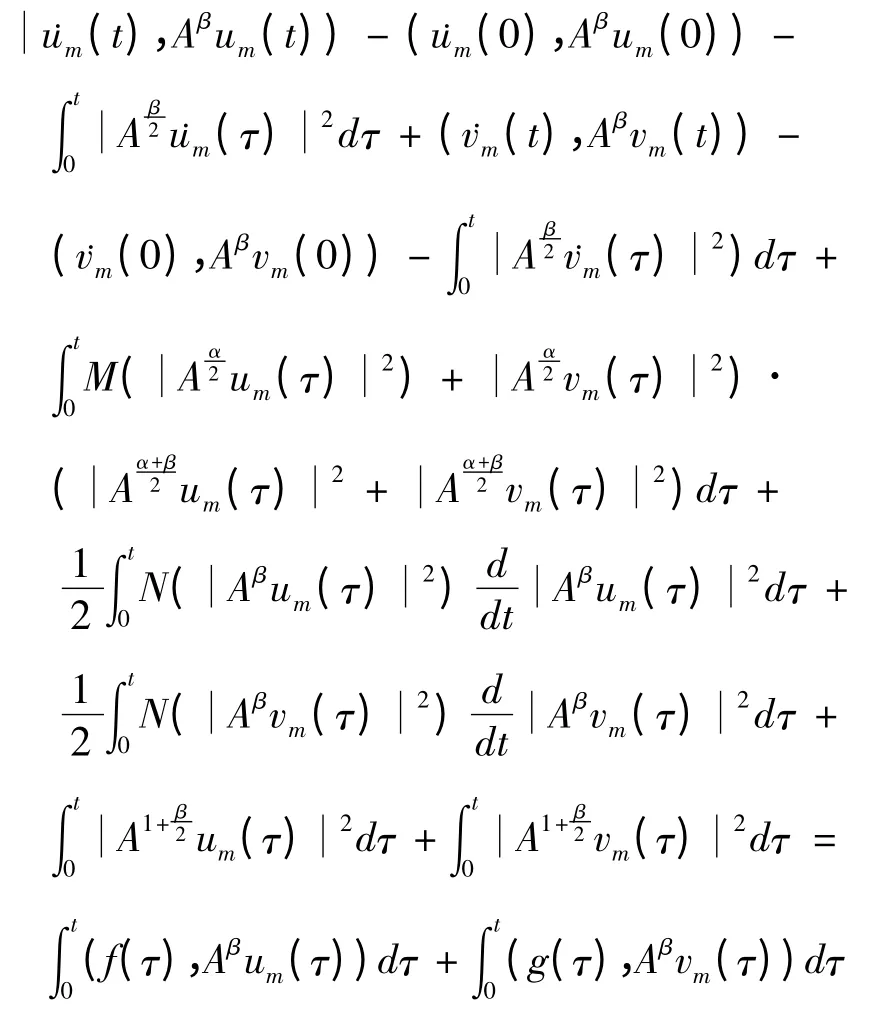
所以
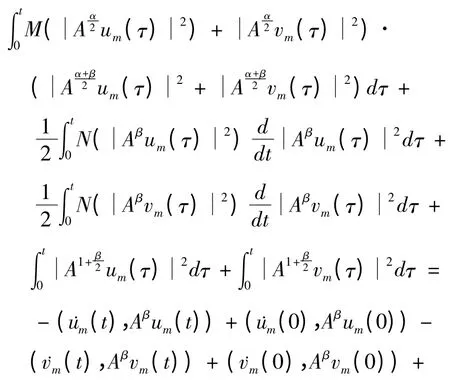
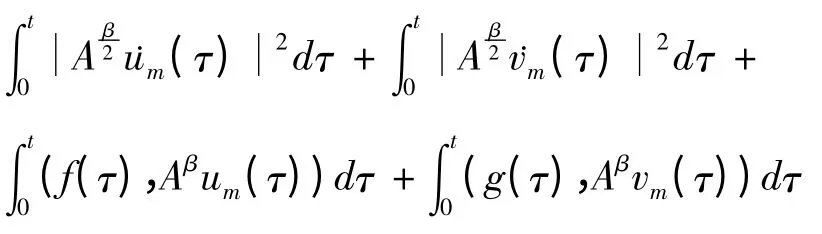
因M(z)≥m0,N(z)≥n0,所以
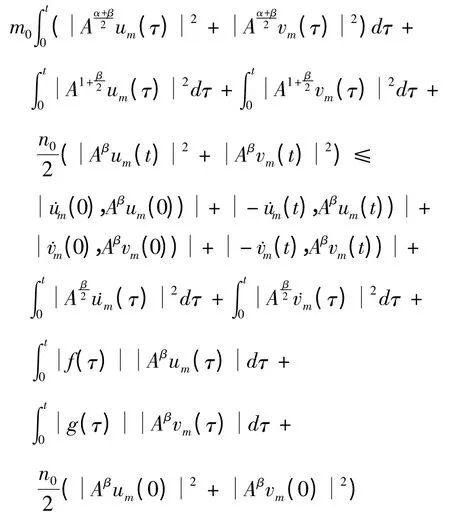
即
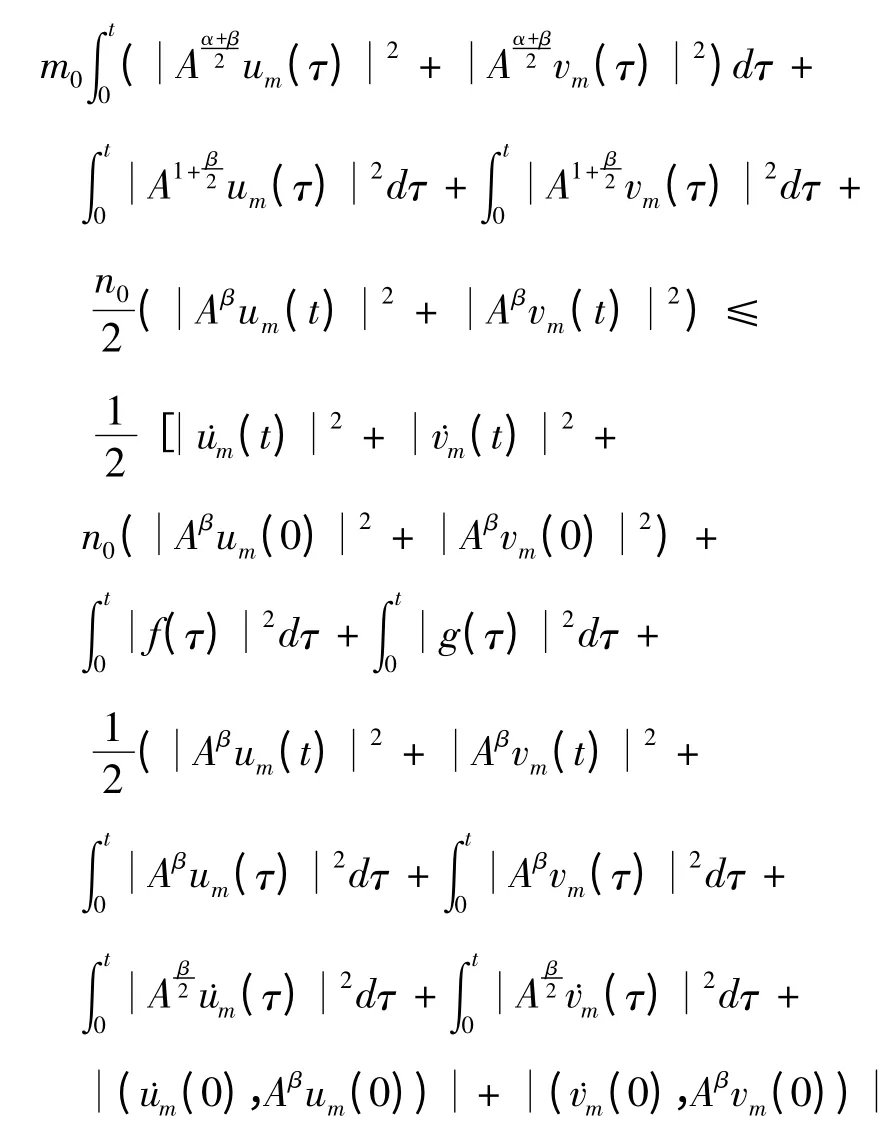
所以
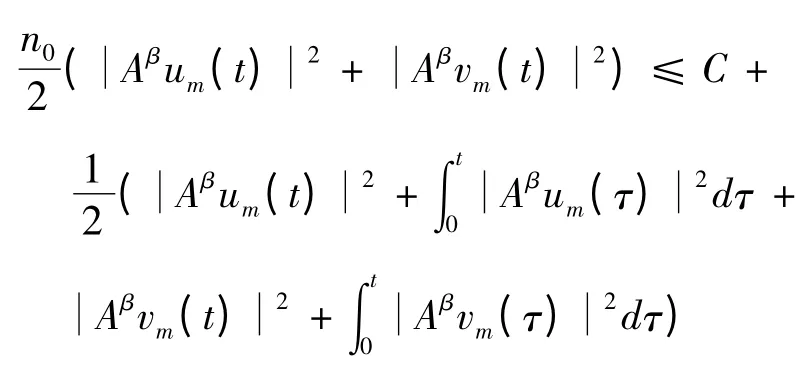
对上式应用Gronwall不等式得
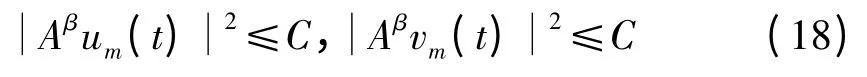
且
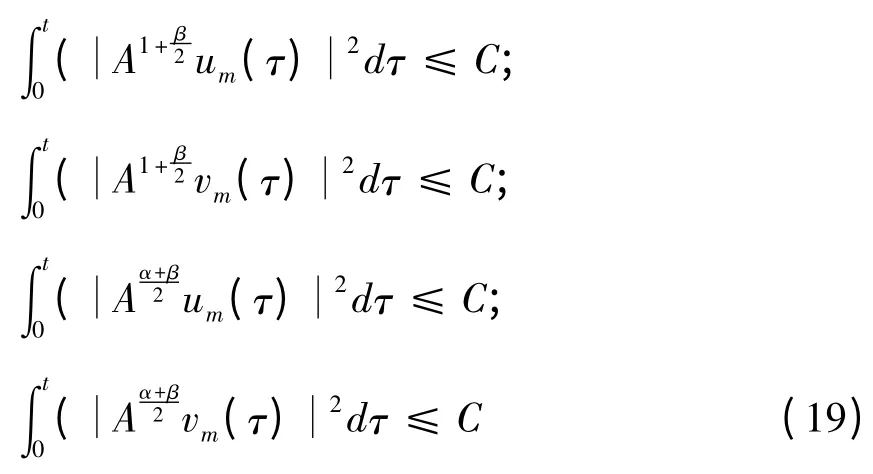
由(15),(19)知{um},{vm}∈L2(0,T;D由Aubin-Lions[5]的紧性理论知,分别存在{um},{vm}的子序列{uμ},{vμ}及函数u,v使得{uμ},{vμ}在L2(0,中分别弱收敛于在L2中分别弱收敛于也˙u,˙v.
进一步可证χ=u,η=v在L∞(0,T;V∩D中成立;在中成立.
现在固定j,取μ>j,可证得
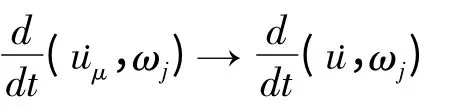
在D'(0,T)中收敛;
在D'(0,T)中收敛;
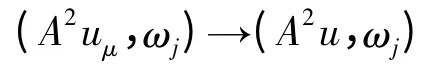
在L∞(0,T)中弱*收敛;

在L∞(0,T)中弱*收敛;
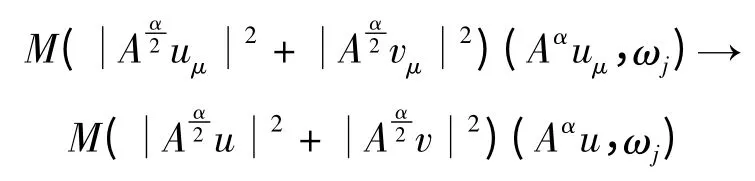
在L∞(0,T)中弱半收敛;
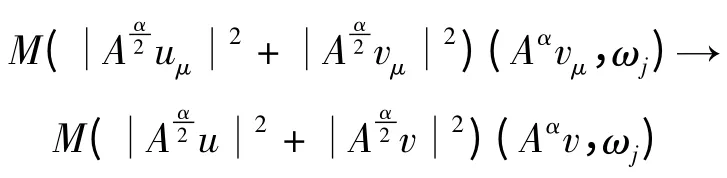
在L∞(0,T)中弱半收敛;
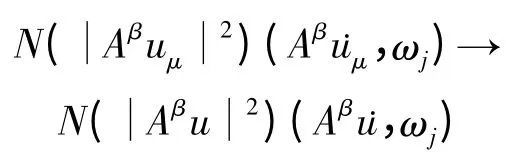
在L∞(0,T)中弱*收敛;
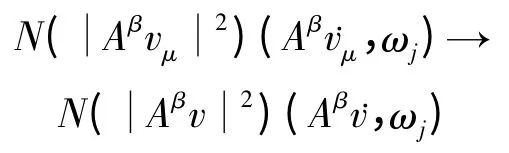
在L∞(0,T)中弱*收敛.
令μ→∞,则m→∞,再由基{ωj)在V中的稠密性,故∀φ∈V,当时,(u,v)在D'(0,T)中满足方程(4),所以问题(1),(2)的弱解存在.
再证定理中的弱解满足初始条件(5),引入连续函数空间
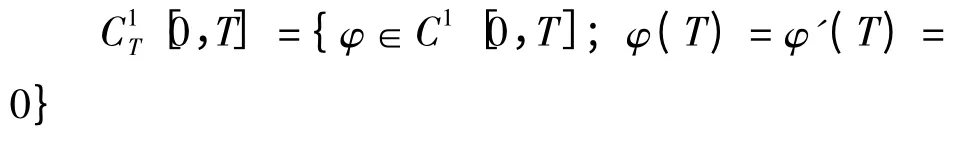
3 结论
本文研究了一类抽象耦合非线性梁方程组在Hilbert空间中的初值问题,并证明了方程组的整体弱解的存在性和解的收敛性.
1 Pedro Pablo Durand Lazo.Global solutions for a nonlinear wave equation.Applied Mathematics and Computation,2008,(200):596~601
2 李润民,张建文.一类抽象非线性梁方程的整体解.太原理工大学学报,2010,41(4):449~452(Li R M,Zhang J W.The global solution for an abstract nonlinear beam equation.Journal of Taiyuan,University of Technology,2010,41(4):449~452(in Chinese))
3 张建文,丁霞霞.一类耦合非线性方程组的整体解.数学的实践与认识,2011,41(13):202~207(Zhang J W,Ding X X.The global solution for a coupled nonlinear equations.Mathematics in Practice and Theory,2011,41(13):202~207(in Chinese))
4 Ball J M.Intial-boundary value problems for an extensible beam.Journal of Mathematical Analysis and Applications,1973(42):61~88
5 Lions J L.Quelques methodes de resolution des problemes aux limites non lineaires.Dunod:Gauthier-Villars,Paris,1969

