Birkhoff系统的广义斜梯度表示*
梅凤翔 吴惠彬
(1.北京理工大学宇航学院,北京 100081)(2.北京理工大学数学学院,北京 100081)
引言
梯度系统对研究积分和解的稳定性十分方便.文献[1]研究了通常梯度系统的性质,文献[2]讨论了斜梯度系统.有关力学系统与梯度系统的研究已有一些结果,如文献[3-8].通常斜梯度系统中的函数不包含时间.若包含时间,则称为广义斜梯度系统.广义斜梯度系统对研究非定常力学系统解的稳定性有重要价值.有关Birkhoff系统的稳定性研究大多限于定常系统[9].本文期望借助广义斜梯度系统来研究一般Birkhoff系统的稳定性.
1 广义斜梯度系统
广义斜梯度系统的微分方程有形式
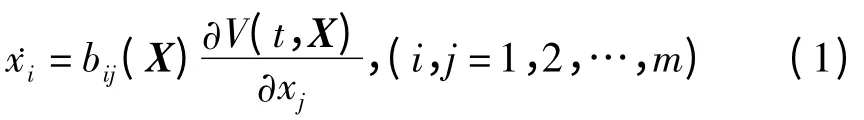
这儿及以后我们约定:同一项中,相同的活动指标表示对其求和,其中bij(X)=-bji(X),X=(x1,x2,…,xm).若V不含时间t,则式(1)成为通常斜梯度系统.
按方程(1)求˙V,得

由(bij)的反对称性质,上式右端第二项为零,于是有

2 Birkhoff系统的梯度表示
Birkhoff系统的微分方程有形式[9-10]
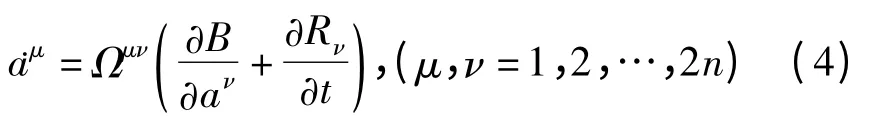
其中B=B(t,a)为Birkhoff函数,Rμ=Rμ(t,a)为Birkhoff函数组,且
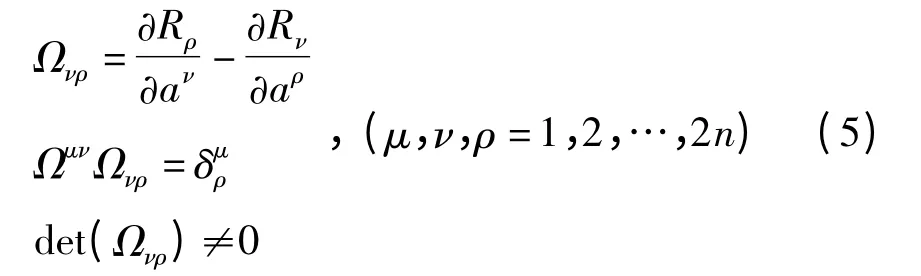
方程(4)一般还不能成为广义斜梯度系统(1).如果存在反对称矩阵(bμν(a))和函数V=V(t,a)满足下式
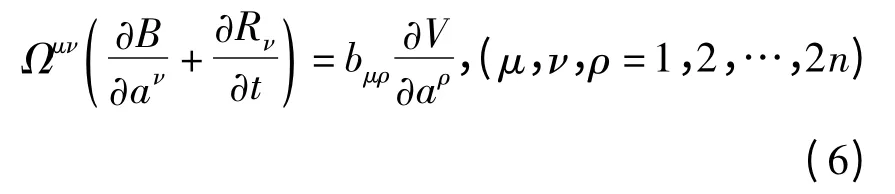
则它可成为广义斜梯度系统(1).
对半自治Birkhoff系统,有
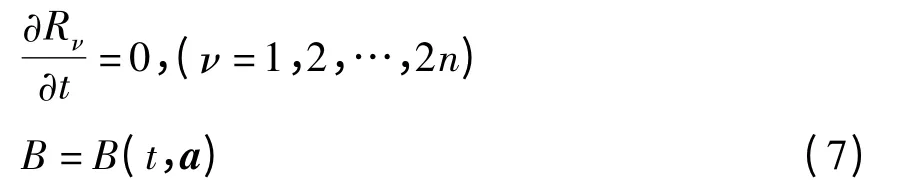
此时,式(6)成为

只要取

则Birkhoff系统成为广义斜梯度系统.此时,若B正定,且有则解是稳定的.
3 算例
例1 Birkhoff系统为
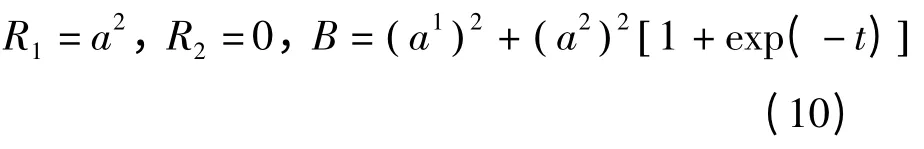
试将其化为广义斜梯度系统,并研究其零解的稳定性.
解:由R1=a2,R2=0得
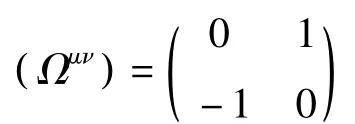
取
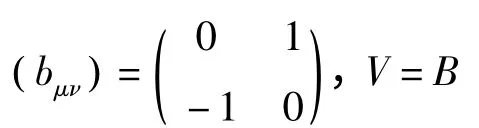
因V在a1=a2=0邻域内正定,且有

故零解a1=a2=0是稳定的.
例2 Birkhoff系统为
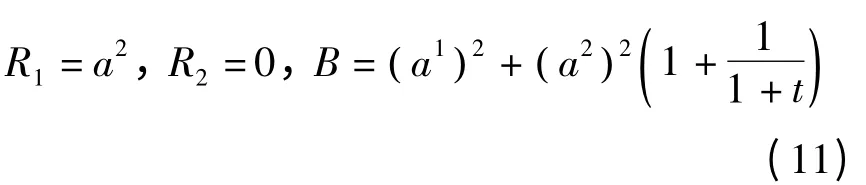
试将其化为广义斜梯度系统,并研究其零解的稳定性.
解:由R1=a2,R2=0得

取

则其成为一个广义斜梯度系统.V在a1=a2=0邻域内正定,且有
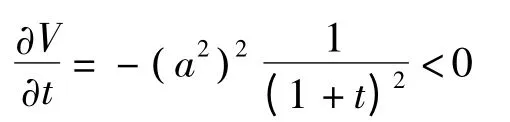
因此,零解a1=a2=0是稳定的.
4 结论
在非定常力学系统稳定性研究中,Lyapunov函数的构造是一大难题.本文首先提出了广义斜梯度系统并研究了它的性质,然后将非自治Birkhoff系统在一定条件下化成广义斜梯度系统,并利用广义斜梯度系统来构造Birkhoff系统的Lyapunov函数,从而解决了一些非自治Birkhoff系统的稳定性问题.
1 Hirsch M W,Smale S.Differential equations,dynamical systems and linear algebra.New York:Academic Press,1974
2 McLachlan R I,Quispel G R W,Robidoux N.Geometric integration using discrete gradients.Philosophical Transactions of the Royal Society A,1999,357:1021~1045
3 楼智美,梅凤翔.力学系统的二阶梯度表示.物理学报,2012,61(2):024502,1~4(Lou Z M,Mei F X.A second order gradient representation of mechanics system.Acta Physica Sinica,2012,61(2):024502,1~4(in Chinese))
4 梅凤翔,崔金超,吴惠彬.Birkhoff系统的梯度表示和分数维梯度表示.北京理工大学学报,2012,32(12):1298~1300(Mei F X,Cui J C,Wu H B.A gradient representation and a fractional gradient representation of Birkhoff system.Journal of Beijing Institute of Technology,2012,32(12):1298~1300(in Chinese))
5 梅凤翔.关于梯度系统.力学与实践,2012,34(1):89~90(Mei F X.On the gradient system.Mechanics in Engineering,2012,34(1):89~90(in Chinese))
6 梅凤翔,吴惠彬.广义Birkhoff系统的梯度表示.动力学与控制学报,2012,10(4):289~292(Mei F X,Wu H B.A gradient representation for generalized Birkhoff system.Journal of Dynamics and Control,2012,10(4):289~292(in Chinese))
7 梅凤翔,吴惠彬.广义Hamilton系统与梯度系统.中国科学:物理学 力学 天文学,2013,43(4):538~540(Mei F X,Wu H B.Generalized Hamilton system and gradient system.Scientia Sinica Physica,Mechanica&Astronomica,2013,43(4):538~540(in Chinese))
8 梅凤翔.分析力学(Ⅱ).北京:北京理工大学出版社,2013(Mei F X.Analytical Mechanics(Ⅱ).Beijing:Beijing Institute of Technology Press,2013(in Chinese))
9 梅凤翔,史荣昌,张永发,吴惠彬.Birkhoff系统动力学.北京:北京理工大学出版社,1996(Mei F X,Shi R C,Zhang Y F,Wu H B.Dynamics of Birkhoffian system.Beijing:Beijing Institute of Technology Press,1996(in Chinese))
10 Santilli R M.Foundations of theoretical mechanicsⅡ.New York:Springer-Verlag,1983

