不完全信息下供应链组合激励机制研究

李福星，谢铁军

（北京科技大学 数理学院，北京 100083）

不完全信息下供应链组合激励机制研究

李福星，谢铁军

（北京科技大学 数理学院，北京 100083）

针对不完全信息下两级供应链的组合激励机制进行了研究。首先，对完全信息下供应链处于集中与分散两种模式进行了博弈分析。其次，设计出不完全信息下两种激励机制模型，通过改进最优控制理论中的变分法求解出激励机制模型。最后，通过数值仿真，验证了两种激励机制模型均能够实现供应链整体绩效的帕累托改善。

不完全信息；供应链；销售努力；组合激励机制

1 引言

随着全球竞争的加剧和科学技术的发展，越来越多的企业开始运用供应链管理策略来达成企业内外环境的协同，进行一体化管理，以提高客户的满意度，提高企业的核心竞争力。21世纪真正的竞争不是企业与企业之间的竞争，而是供应链和供应链之间的竞争。供应链作为一个新兴的研究领域始于上世纪80年代，研究主题分为战略管理、伙伴关系、物流、最优化、市场及组织。

Cachon[1]对目前已有的供应链管理中的协调方式进行了梳理，总结了供应链协调的各类合同与机制。Corbett等[2]对不完全信息下，垄断供应商在供应链中的最优合同进行了研究。Esmaeilia[3]对出售者—购买者模式下基于信息不对称情形，提出了多个不同的合作模式和策略。庄品[4]研究了非对称信息下供应链激励协调问题。蒲勇健、郭心毅[5]将行为经济学中的公平偏好的研究结论引入到委托—代理模型中，研究了代理人同时关注物质效用和公平分配情况下的最优激励契约和激励效率。韩敬稳、赵道致[6]研究了强势零售商压低供应商批量价格的行为对零售商主导型供应链绩效的影响，指出恢复供应链上下游公平的交易状态是对供应链绩效进行帕累托改进的重要途径之一。周扬、石岿然[7]通过重复博弈分析和数值仿真，研究了供应链提高合作的可能性以及利润分配问题。郎艳怀[8]针对价格弹性需求和非对称信息下两级供应链的激励机制问题进行了研究。陈莎莎等[9]将零售商单位营销支出作为私人信息，研究了供应链激励机制问题。曾顺秋、骆建文[10]对广告影响随机需求且带有二次订货机会的两级供应链中的最优策略进行了研究。

以往对委托—代理模型[11]的研究中，多采用单一的激励机制，本文的研究中采用组合激励机制，即同时运用销售努力补贴和转移支付两种激励方式，设计了具有可操作性的激励机制模型，并进行数值仿真以验证该激励机制能实现供应链整体绩效的帕累托改善。

2 模型假设及参数解释

考虑由一个制造商和一个零售商组成的两级供应链系统，供应链成员均为风险中性，即其效用水平等于期望收益水平。

（1）c：制造商生产单位产品的成本。

（2）w：零售商从制造商处进货的单价。

（3）e：零售商销售努力水平，为零售商的私人信息。e∈[e1,e2]，e在该区间上的分布函数与密度函数分别为F(e)和f(e)。

（4）p：零售商的零售价。

（5）市场需求D(p,e)=m-np+g(e)，其中m为市场规模，假设m足够大，使得市场需求量不会为负；n为价格弹性系数。

（6）g(e)：销售努力e的产出函数，为凹函数，g′(e)＞0表示努力的边际销量为正，g″(e)≤0表示努力的边际销量递减。

（7）φ(e)：销售努力e的成本函数，满足 φ′(e)＞0且 φ″(e)＞0，不妨设其中b为成本系数，b＞0。

（8）q：零售商订货量，只有一次订货机会，故q≥D(p,e)，不考虑零售商缺货。

（9）πm：制造商收益。

（10）πr：零售商收益。

（11）πt：供应链总收益。

由上面的假设和记号得：

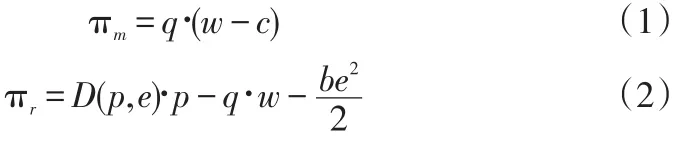
3 完全信息下的博弈分析

完全信息指的是制造商和零售商对彼此的特征（包括战略空间收益函数等）有完全的了解。本文假设制造商处于这个两级供应链的主导地位，零售商处于从属地位，可以选择合作与否。

根据零售商与制造商合作与否，完全信息下博弈模型可以分为集中控制模型和Stackelberg模型。

3.1 集中控制模型博弈分析

集中控制情形下，制造商与零售商合作，以实现该供应链系统收益最大化。供应链整体收益函数为：

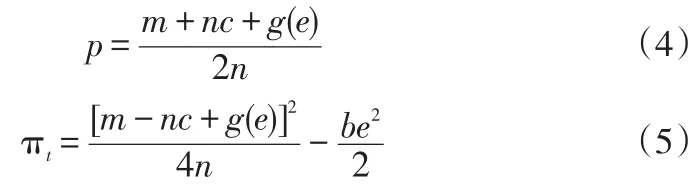
3.2 Stackelberg模型博弈分析

在Stackelberg博弈下，制造商为发起者，首先选择售给零售商的单价w，零售商在观测到w后，确定最优零售价p和最优订货量q。

零售商面临的规划问题：

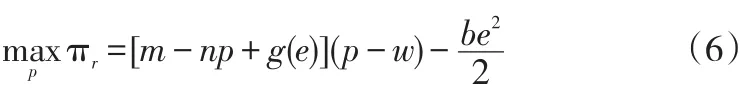
求解得：

由于信息是对称的，制造商预测到零售商将选择决策策略{p,q}。因此制造商面临的优化问题为：

求解得：

此时有：

供应链总收益：

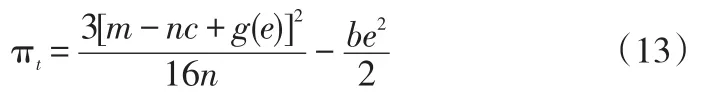
4 不完全信息下的博弈分析

实际生活中，供应链成员之间信息并不是完全的，零售商出于自身利益，可能会隐藏私人信息，以获得可能多的额外收益。根据Myerson在1970年给出的著名的显示原理，制造商只需要考虑激励机制的设计，便能诱使零售商如实申报自己的私人信息，以获得最大的预期收益。

以下假设在该两级供应链中，制造商是委托人，没有私人信息，零售商是代理人，销售努力水平e为其私人信息，每次合作时，零售商首先申报自己的努力水平而真实努力水平为e。

为了使代理人如实申报自己的私人信息e，委托人设计如下激励机制其中为激励批发价为激励转移支付。记代理人接受激励机制时的收益为委托人的收益为由分散决策下Stackelberg博弈可知：

那么激励相容约束相当于求解以下极值问题：

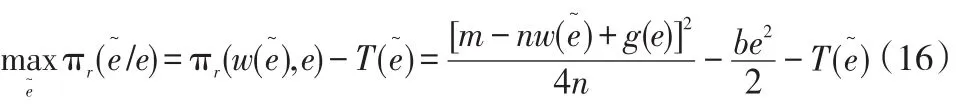
该极值问题的一阶条件为：

即：

因此要促使代理人如实申报自己的销售努力水平，要求当且仅当e～=e时，上式取极大值，激励相容约束转化为：

个人理性约束要求代理人从接受激励机制中得到的期望收益不小于不接受激励机制时能得到的预期最大收益，即保留收益π0。那么在零售商销售努力信息不对称的情况下，制造商激励机制的设计转变为求解以下的优化模型I：

求解上述模型I，首先忽略个人理性约束(IR)，将该规划问题转变为一个最优控制问题。

将u(e)视为控制变量，w(e)、T(e)视为状态变量。

建立哈密顿函数：

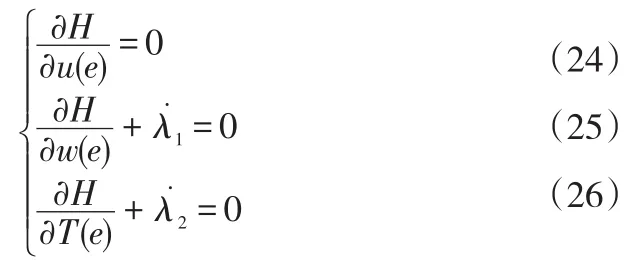
由式（23）得：

由式（24）得:

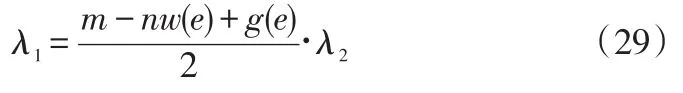
求导得：

由（26）式得：

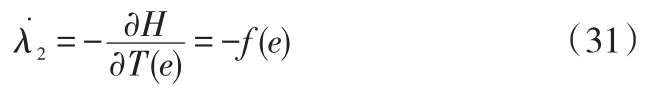
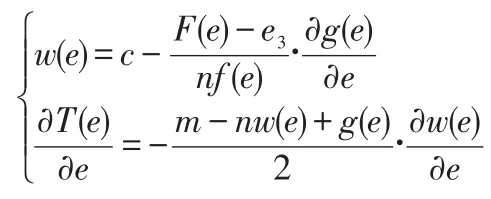
下面讨论个人理性约束条件(IR)，零售商销售努力水平对收益的影响：

激励相容约束的推导如下：

将u1(e)、u2(e)视为控制变量，w(e)、ξ(e)、T(e)视为状态变量。

应用变分法求解上述最优控制问题，令：

引入拉格朗日乘子向量λ(e)=[λ1(e),λ2(e),λ3(e),λ4(e)]T，构造下列泛函：

引入哈密顿函数H，令：

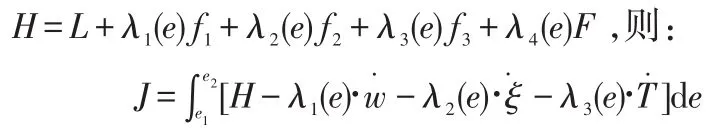
利用分部积分变换后，得：

根据泛函极值存在的必要条件，式（37）取极值的必要条件是一阶变分为零，即δJ=0。在式（37）中引起泛函变分的是控制变量U(e)和状态变量X(e)的变分δU(e)和 δX(e)，将式（37）对它们分别取变分，则得：

式中δU=[δu1,δu2]T；δX=[δw,δξ,δT]T。

由于应用了拉格朗日乘子法后，按无约束问题处理，因此U(e)和X(e)可看作彼此独立的，δU和δX不受约束，即δU和δX是任意的。换言之，δU≠0，δX≠0，因此从式（38）可得泛函极值存在的必要条件为：

将上述必要条件展开即有：

由H的表达式求偏导带入式（39）-式（43）解得：

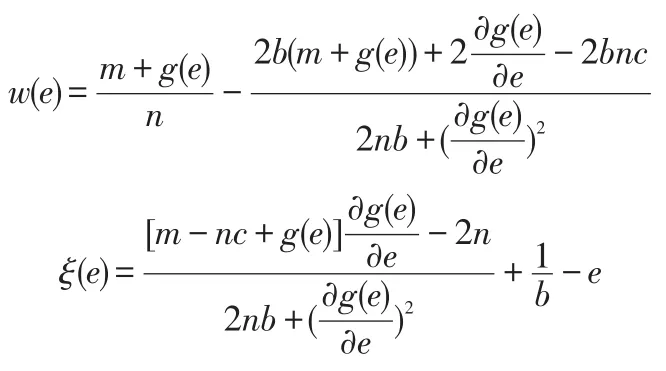
将w(e)与ξ(e)的表达式带入T(e)的表达式解得：

5 数值仿真

以下通过数值仿真来观察完全信息与不完全信息情况下供应链系统的总体收益。取上述模型中的参数分别为：m=2 000、n=20、c=5、b=1、e1=0、e2=400、e3=1和e4=1，取销售努力的产出函数g(e)=ke，其中k=3。销售努力的取值范围为[0,400]，在该区间上服从均匀分布，分布函数和密度函数分别为利用MATLAB进行仿真，结果如图1所示。

图1 三种情况下，供应链系统总收益比较

从图1可以看出，销售努力在区间[50,400]时，不完全信息激励机制的系统总收益介于集中控制时系统总收益与Stackelberg博弈系统总收益之间，说明激励机制实现了供应链系统总收益的帕累托改善。图1也说明了随着销售努力的增大，供应链系统的总收益先增大后减小，存在极大值，与现实中情况比较符合。但是当销售努力在区间[0,50]上时，模型I激励机制下的系统总收益小于Stackelberg博弈系统总收益，即激励机制在该区间上失效，于是采用模型II激励机制，结果如图2所示。

从图2可以看出，模型II激励机制在区间[0,50]上，有效解决了模型I激励机制失效的问题，并且实现了供应链系统总收益的帕累托改善。

图2 两种激励机制情况下，供应链系统总收益比较

6 结语

本文对不完全信息下两级供应链的组合激励机制进行的研究，设计出了两种激励机制，每一种激励机制都有一定的适用范围，可以根据私人信息的具体情况求解得到适用条件，从而选择不同的激励机制。本文同时得出以下结论：在不完全信息下，委托人设计的激励机制可以实现供应链整体绩效的帕累托改善；组合激励机制的设计在局部范围内明显优于单一激励机制的设计。

[1]Cachon G.Supply chain coordination with contracts[M].Graves S,de Kok T.Handbooks in Operations Research and Management Science: Supply Chain Management.North-Holland,2003.

[2]Corbett C,Zhou Deming,Tang C.Designing supply contracts:contract type and information asymmetry[J].Management Science,2004,50(4): 550-559.

[3]Esmaeilia M,Zeephongsekulb P.Seller-buyer models of supply chain management with an asymmetric information structure[J].International Journal of Production Economics,2010,123(1):146-154.

[4]庄品,赵林度.非对称信息下供应链协调激励机制研究[J].物流技术, 2007,26(1):81-84.

[5]蒲勇健,郭心毅.基于公平偏好理论的激励机制研究[J].预测,2010,29 (3):6-12.

[6]韩敬稳,赵道致.零售商主导型供应链绩效的行为博弈分析[J].管理科学,2012,25(2):61-68.

[7]周扬,石岿然.制造商主导的供应链合作及利润分配研究[J].科技管理研究,2012,31(5):136-140.

[8]郎艳怀.非对称信息和弹性需求下的供应链激励机制研究[J].中国管理科学,2012,20(5):106-111.

[9]陈莎莎,谢铁军.非对称信息供应链激励机制模型研究[J].物流技术，2014,33(9):312-315.

[10]曾顺秋,骆建文.二次订货机会下基于交易信用的供应链组合激励机制[J].上海交通大学学报,2014,48(2):277-281.

[11]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,1996.

Study on Supply Chain Combined Motivation Mechanism under Incomplete Information

Li Fuxing,Xie Tiejun
(School of Mathematics&Science,University of Science&Technology Beijing,Beijing 100083,China)

In this paper,we studied the combined motivation mechanism of a two-echelon supply chain with incomplete information. First we had a game analysis of the supply chain with complete information when it was of the centralized and distributive modes respectively, then designed the model of the two motivation mechanisms under incomplete information,and at the end,through a numerical simulation, demonstrated that both motivation mechanism could realize the Pareto improvement of the supply chain.

incomplete information;supply chain;sales effort;combined motivation mechanism

F274

A

1005-152X(2015)11-0150-05

10.3969/j.issn.1005-152X.2015.11.041

2015-10-04

李福星（1992-），男，河南信阳人，硕士研究生，研究方向：运筹学、博弈论；谢铁军（1962-），男，副教授，硕士生导师，研究方向：最优化理论与算法、博弈论。