关于余割函数不定积分多种形式的统一
2015-03-01 03:33周传斌
亚太教育 2015年4期
文/周传斌
关于余割函数不定积分多种形式的统一
文/周传斌
不定积分是高等数学的核心知识,任何一个函数的不定积分形式并不统一,但本质是相同的。余割函数是一类非常重要的函数,理解透彻余割函数的不定积分是学好高等数学的关键。
不定积分;统一;余割函数
一个函数的不定积分既不是一个数,也不是一个函数,而是一族函数,称为原函数族。函数的不定积分形式并不唯一,只要通过逆向求导能得到被积函数就是正确的。
一、余割函数的定义

二、第一类换元积分法(凑微分)
定理:设函数f(t)存在原函数F(t),t=α(x)可导,则有公式

此公式称为不定积分的第一换元积分公式,其又称为“凑微分法”。
三、余割函数通过凑微分法呈现出多种形式的不定积分
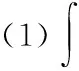






三种方法各有优缺点,虽然形式多样化,但最终都实现了本质上的统一。
四、结语
本文是作者初次接触高等数学教学的一点感受,疑惑的是余割函数是否还有更多的不定积分求法呢?这就需要进一步研究讨论了!作为一名人民教师,只有用爱去教育、用心去工作,才能成为享受教育工作的人;才能成为高端职业教育的领航者;才能与西航学子平等共生、共创传奇。
[1]刘建勇.高等数学[M].第一版.长沙:国防科技大学出版社,2013.02,67-69.
[2]同济大学数学系.高等数学[M].第六版.北京:高等教育出版社,2009.07.
[3]陈珠社.怎样突破第一类换元积分法[J].《数学学习与研究》2011.17.
O
A
2095-9214(2015)02-0117-01
四川泛美教育投资有限责任公司;四川西南航空职业学院)
猜你喜欢
中学生数理化·七年级数学人教版(2021年12期)2021-12-31
课程教育研究·新教师教学(2015年12期)2017-09-27
中央民族大学学报(自然科学版)(2017年2期)2017-06-11
中学生数理化·高三版(2017年2期)2017-04-21
福建中学数学(2017年1期)2017-04-21
西安工程大学学报(2016年6期)2017-01-15
振动工程学报(2015年2期)2015-03-01
燕山大学学报(2014年4期)2014-03-11
河南科技(2014年15期)2014-02-27

