纵向船用气囊下水过程数值分析

方晓波，余 龙，刘光武，周信林，杨 启

(1.上海交通大学海洋工程国家重点实验室，上海200240)

(2.中国船舶及海洋工程设计研究院，上海200011)(3.武汉理工大学交通学院，湖北武汉430063)(4.赛尼尔(上海)系统有限公司，上海200122)

自1981年以来，纵向船用气囊下水(以下称为气囊下水)经过了30多年的探索和实践，在国内造船业得到广泛使用，气囊下水船舶自重记录不断刷新，目前下水船舶最大载重量已达7万吨.下水的船舶种类包括常规船舶、海洋平台以及疏浚工程船等.船舶气囊下水的安全性一直是关注的热点，长久以来主要依赖于气囊产品的承载力不断提高，以及通过实船下水的不断摸索.然而，船用气囊承担的载荷不断提高，施工的风险也随之增加，仅靠过去的经验已经不能面对新环境的挑战，亟需理论基础支持，这已是相关专家的共识.

到目前为止，浙江工业大学的研究人员在下水过程模拟和测试方面做了大量工作，对5艘2万吨级船舶气囊下水过程进行了实测，揭示气囊下水最大倾角发生在艉落阶段且仅有1.8°，下水过程倾角变化平缓［1］，并进行了相关的静力和动力下水过程分析计算程序研究［2-3］.济南昌林气囊有限公司的研究人员进行了长期的研究，建立了气囊纵向下水计算方法，提出气囊下水过程中尾跌落和尾上浮现象不再明显，并对气囊压力和滚动阻力计算方法进行研究［4］.基于囊体材料特性的最新研究成果，分析并设计了一套模拟气囊下水的静态计算程序:该程序通过输入船舶参数，所选用的气囊参数和船台参数，即可得到整个气囊下水过程中的倾角变化、浮力变化、各个气囊的承载力和承载高度，同时，预判下水过程的上浮点和气囊的安全性［5］.

1 气囊下水过程

1.1 气囊无损失阶段

该阶段即船尾未超出主船台末端(整个船舶支撑在主船台上).该过程中所有气囊都产生一定承载力，维持船舶的自平衡.这一阶段，主要校核气囊承载力对重心的力矩是否满足要求，以及船底各个部分受力是否安全.

1.2 气囊损失阶段

在该阶段，船舶下滑，气囊会跟随船体一起滚入水中，当船尾第一个气囊离开主船台进入副船台后，气囊便会浮起，失去作用，在这个阶段中，随着船舶下滑距离的递增，承载气囊数量逐渐减少.

1.3 无气囊阶段

即整个船舶进入到副船台.当船首离开船台末端时，所有气囊均已浮起，此时船舶下水与滑道下水过程相同.

2 理论研究

根据船舶下水基本理论推广到气囊下水受力，图1为船舶气囊下水基本受力图.在静态分析中，牵引力和摩擦力对船舶的下水不产生影响，故暂时不予考虑.参考以前的相关研究［6-7］，在气囊未损失的情况下(即船舶整个在主船台上)，承载力和浮力对重心的力矩平衡:式中:FB为船舶入水部分所受浮力(t);Ni为各气囊承载力(t);lB0为浮力对船舶重心的力臂(m);li0为各气囊承载力对船舶重心的力臂(m);各力矩以逆时针为正.

在气囊损失阶段，即船舶半悬挂在主船台上，进行承载力、重力和浮力对主船台末端的平衡.

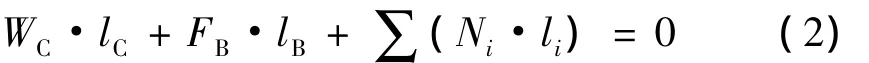
式中:WC为船舶下水重量(t);lC为船舶重力对主船台末端的力臂(m);lB为入水部分浮力对主船台末端的力臂(m);li为各气囊承载力对主船台末端的力臂(m).

垂向平衡公式:

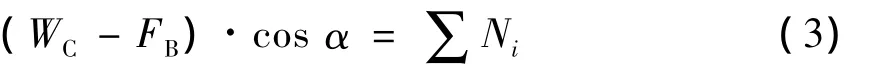
式中:α为船舶相对水平面的倾角(rad).

图1 船舶气囊下水基本受力Fig.1 Display of forces acting during launching with airbags

3 气囊下水计算程序

3.1 程序简介

程序在研究常规船台下水程序的基础上，开发了气囊下水模拟计算程序(以下简称为程序)(图2).

该程序包含以下主要功能:

1)计算船舶变倾角变吃水下的浮力大小以及浮心位置.

2)模拟并计算常规船台下水过程，输出下水曲线、参数并预报下水结果.

3)模拟并计算纵向气囊下水过程，输出下水曲线、参数、各个气囊承载情况和下水结果.

在气囊下水计算程序中，对船用气囊的参数以及高度与承载力计算采用了理论模型［8］，压缩量及支承力结果与实验数据［9］的比较见图3.

图2 下水程序界面Fig.2 Interface of launching program

图3 气囊承载力与压缩量关系曲线Fig.3 Relations between bearing forces and compression values

3.2 基本假设

为了方便程序计算和模拟，在尽可能不损失精度的前提下，对一些下水要素做了一定简化.

1)默认船体、船台均为一刚性体，不发生部分变形.

在程序设计中，暂不考虑船体挠度以及船台变形的影响，则气囊承载力呈梯形分布(图4)，从计算结果上来看，此假设不会对计算结果造成明显误差.

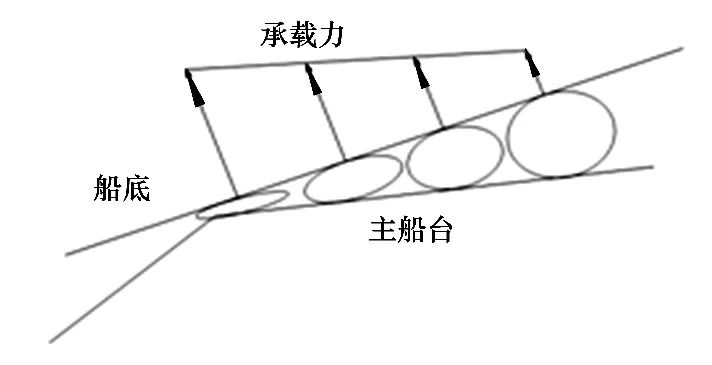
图4 气囊承载力梯形分布Fig.4 Trapezoidal distribution of bearing forces

2)将气囊作为等长度、等间距的二维柔性墩木.

所谓柔性墩木，即假设气囊与船体不发生相对运动，如同滑道下水过程中的支撑墩木，始终固定于船底某个位置.由于气囊的布置密集，以及首尾气囊的实时补充，使得单位长度内的气囊数量不发生改变，故这种假设是合理的.

3)进入的副船台的气囊无承载力.

当气囊滚入副船台的时候，大多数气囊都会浮起失去作用，故作此假设.对比实际情况，此假设下的计算结果偏于安全，可作为安全裕度考虑在内，故此假设合理.

4)摩擦力、牵引力力矩不计.

3.3 程序流程

程序的输入主要有船舶参数、船台参数和气囊布置参数.其中船舶参数包括主尺度、下水重量、重心和Bonjean′s curves(邦戎曲线)数据等;船台参数包括主副船台倾角和长度、下水潮位高度等;气囊布置参数包括气囊直径、数量、间隔、首位位置、气囊承载力回归公式等.

程序的输出包括下水过程中不同滑移距离下的倾角、浮力、浮心位置、各个力矩的数据，以及每个气囊的承载力和工作高度，同时预报下水过程中的上浮点、正浮点、最大气囊受力及位置、是否发生尾落等.

程序先通过式(3)用反复迭代气囊压缩量的方法完成垂向初步平衡，再通过增减船舶倾角达到式(1)或式(2)的平衡，其中一旦倾角变化后都需重复式(3)的工作，因此，在每一个滑程下都是一个大型迭代的计算过程，从而达到准静态平衡的效果.流程如图5所示.

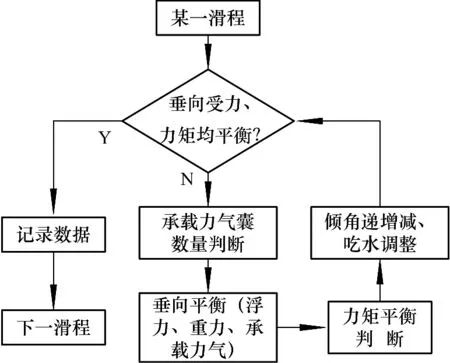
图5 气囊下水静态模拟计算程序流程Fig.5 Flowchart of the static simulation program

4 对常规纵向船台滑道下水计算及与FORAN软件计算结果对比

为了验证程序的可靠性以及完整性，应用国际知名的FORAN软件进行了对比性分析.FORAN软件是世界上应用最为广泛的大型造船专业软件之一，全球用户包括了170家以上的设计公司和造船厂，近年来更以较快的速度在全球推广.运用FORAN软件中的Launch计算模块就某大型散货轮模型进行了下水计算，并根据其计算结果进行对比分析，对比结果表明程序在计算过程和结果上都比较令人满意，同时程序能够模拟船舶的倾覆情况和尾落现象，并记录数据.而FORAN软件则更为全面，可以提供下水过程中的剪力和弯矩等更多的信息.

表1为相同倾角、吃水下的浮力对比，FORAN软件根据所导入的型线进行计算求解，程序从船舶Bonjean′s curve(邦戎曲线)数据入手求解.从对比结果来看，浮力计算误差很小，程序设计是可靠的.

表1 船舶静水力计算对比表Table 1 Comparison of hydrostatic calculations between program and FORAN

表2为2种程序在相同的输入条件下模拟船舶常规船台下水的下水结果，从对比结果来看，程序的计算结果与FORAN的计算结果基本一致.起墩时，重力对首支点力矩非常接近，误差在0.1%左右.两种计算结果在各自上浮点时的倾角和各力矩结果一致.

表2 常规滑道下水本程序计算结果与FORAN计算结果对比Table 2 Comparison of launching with slipway calculations between the program and FORAN

从图6中可知，FORAN计算的浮力曲线和程序计算所得的浮力曲线基本一致，程序有较高的计算精度.在滑程后半段程序浮力曲线产生跃升的原因是没有考虑水的阻力等其他因素，导致浮力增大，而FORAN程序模型更为全面，这也是程序需进一步完善的方向.

图6 下水曲线对比Fig.6 Comparison of the launching buoyance curves

5 气囊下水计算

选用70000 t散货轮为算例，该船舶于2010年12月初成功用气囊下水.结合该船舶的基本参数和船台参数，用程序模拟得到了下水结果.在整个气囊下水过程中有两处需要校核气囊压力值:一是在船舶起墩时候;二是在船舶重心到达船台末端处.

图7 70000 t散货轮气囊布置示意Fig.7 Airbag arrangement of a 70000 tons bulk carrier

程序中的气囊布置情况根据70000t实际下水气囊布置(图7)稍作简化，默认所有位置气囊保持相同的平均工作长度为24 m，且各个气囊间隔分布均匀，尾部气囊从船尾支点处开始布置(尾垂线靠前10.8m)，首部最后一个气囊位于船首支点处(艏垂线偏后5.4m).

5.1 气囊承载力计算结果及分析

选用最大受力气囊附近的5个气囊绘承载力变化曲线(图8)，最大受力气囊为28号气囊，该气囊在89m前承载力成平稳上升，在89m处到达主船台末端，此时承载力为1397.88 t.在这之后，气囊进入副船台浮起，不在提供承载力.

图8 各个滑移距离下最大气囊受力值趋势曲线Fig.8 Stress of different airbags varies with slip distances

虽然单个气囊在随滑程增加的同时，承载力在增大，但所有气囊总承载力却在减小(图9)，这是因为船舶在下滑过程中，所受浮力不断增大造成的.在船舶完成正浮前，即180m左右，气囊总承载力有回升情况出现，结合下水曲线可知，这是由于在船舶上浮阶段末端，达到正浮前，浮力随着倾角大幅度减小，相应的，为了达到船舶自平衡，气囊支反力就增大，造成总承载力曲线回升现象.

图9 气囊总承载力变化曲线Fig.9 Relations of the airbags total capacity with slip distances

程序在运行结束后，会预告最大受力气囊位置以及承载力，本例中受力为1397.88 t，出现在滑移距离89m处，即船舶重心到达船台过渡点时.经过校核，该处承载力在这种气囊的安全承载范围内，故下水是安全的.

5.2 计算结果对比

5.2.1 起墩时重心附近气囊承载力对比(表3)

表3 起墩时船舶重心位置附近气囊承载力Table 3 Bearing forces of airbags at the center of gravity at beginning of the launching

起墩时所有气囊的承载力对船舶重心之矩的总和为283.07t·m，大大小于船舶下水重量乘以两柱间长的1%，船舶有足够的稳定性，所以起墩过程是安全的.

起墩时候，程序计算结果与文献［10］的计算结果有一定偏差，原因归结于以下2点:

1)文献［10］起墩时默认船舶与船台处于0倾角差状态，即各个位置气囊保持同等的工作高度，相同的作用力，而程序默认船舶在起墩时，会根据各个受力对重力的力矩差调整倾角，造成船舶尾倾，经过考证，此设计是合理，更贴近实际情况的.

2)文献［10］计算结果中，气囊的总承载力为13709t，略大于船舶的实际下水重量13000t.故各个气囊承载力普遍偏大，而程序中的气囊总承载力等于船舶的下水重量.(因为船台有一定坡度，重力有一定的分力由牵引绳索抵消).

5.2.2 船舶重心移到船台末端时重心位置附近气 囊承载力对比(表4).

表4 船舶重心到达船台末端时船舶重心位置附近气囊承载力Table 4 Bearing Forces of airbags at the Center of Gravity when it reaches the end of slipway

程序计算结果基本符合文献计算结果.通过本例的计算结果，可以得到以下一般性结论:当船舶倾角大于船台倾角时，每一滑程下最大受力气囊出现在船台末端，而整个下水过程中的最大受力气囊出现在重心移至主船台末端时，此工况为整个下水的危险工况.

5.3 气囊下水与常规船台下水计算结果对比

为了更好地理解气囊下水的优势，对计算分析的大型散货船，不考虑气囊的可靠性以及气囊作用力对船舶局部结构的影响，仅就下水曲线作进一步分析.将70000t散货轮在相同的船台下进行了常规船台下水模拟，并得到了下水过程中倾角变化曲线(图10).

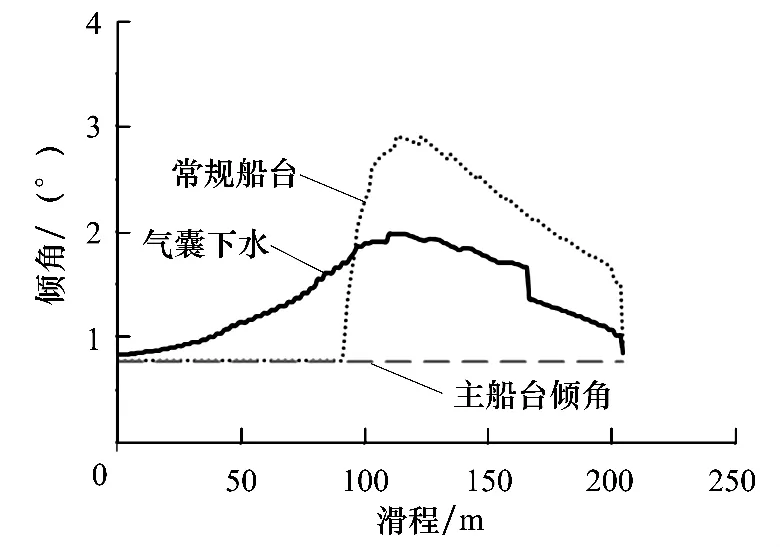
图10 常规船台下水与气囊下水滑移距离-倾角变化曲线Fig.10 Variation of ship trim angle along the slip distances

从图10的对比结果可以明显的看出，滑道下水在重心超过船台末端后，倾角有快速的增大趋势，而气囊下水中，倾角变化是连续且缓慢的，由此可知，气囊下水中船舶的姿态更为平缓，安全系数较好.

其次，常规船台下水过程结束前，倾角有剧烈减小的现象，这标志着船舶发生了“艏落”现象，这是相对危险的.在气囊下水，“艏落”现象则不明显.两种下水均没有“艉落”现象发生，因为其最大倾角均未抵达副船台的倾角值(5.7105°).

图11中，Wc为重力;Fb为浮力;Mw，Mb分别为重力、浮力对船台过渡点的力矩;Mwa，Mba分别为重力、浮力对首支点力矩;D为距离.经过对比可以发现，常规船台在重心到达船台末端前，船舶基本处于平滑状态，浮力力矩都大大小于重力力矩，当重心超过船台末端后，船舶倾角大幅度上升，浮力也随之突变.下水过程中，起伏变化明显.而气囊下水的整个过程都趋于平缓，浮力和浮力矩的平均上升斜率较滑道下水小，浮力对船台末端的力矩都稍大于重力对其的力矩，原因是有气囊的反承载力矩存在.两个下水曲线在重力和浮力力矩平衡之前，即160 m左右都有浮力的大幅度减小情况发生，该情况说明，船舶渐渐处于正浮，浮力减小.

图11 气囊下水与常规船台下水曲线比较Fig.11 Comparison of two kinds of launching computations

6 结论

分析气囊下水过程中船舶的受力情况，结合气囊的承压变形计算模型，建立气囊纵向下水计算分析方法并编制相应程序.从算例分析和与FORAN的对比结果中也可以看出，程序的运行思路和计算过程都是比较完整的，得到的数据和实船的下水数据较为接近.总的来说，此静态模拟计算程序能够完整的模拟气囊下水，并得到详细的下水数据和曲线，且计算结果令人满意，对船舶气囊下水技术的研究有很大的帮助.

对70000 t散货轮下水计算结果表明，该下水设计方案是合理的，下水过程中会不出现气囊压力过大的现象，船舶在整个过程中姿态也比较平稳，没有尾落等现象发生.

但气囊下水的整个过程是一个非常复杂的综合性问题，涉及各个学科领域的知识，在所设计的程序中仍有许多需要改进的地方，比如可以将静态的过程拓展到动态，加入摩擦力和水动力的影响因素，将会得到更贴近实际的计算结果.

References)

［1］ 钱少明，毛亚郎，孙小权.船舶气囊下水过程中船体倾角变化的测试与研究［J］.船舶，2008，6:44-46.Qian Shaomin，Mao Yalang，Sun Xiaoquan.Measurement and research on ship pitch change during process of ship launching by gasbag［J］.Ship ＆ Boat，2008，6:44-66.(in Chinese)

［2］ 孙菊香.船舶气囊下水技术现状与展望［J］.军民两用技术与产品，2010，8:45-48.Sun Juxiang.The present situation and prospect of ship launching with airbag［J］.Dual Use Technologies ＆Products，2010，8:45-48.(in Chinese)

［3］ 黄巧燕，章晓莉，方伊娜，等.船舶气囊下水静力学模型研究与计算［J］.中国水运，2012，12(9):41-44.Huang Qiaoyan，Zhang Xiaoli，Fang Yina，et al.Research and calculation on statics model of the ship launching with airbag［J］.China Water Transport，2012，12(9):41-44.(in Chinese)

［4］ 朱珉虎，孙菊香.船舶气囊纵向下水计算方法的研究［J］.船舶，2009，3:39-44.Zhu Minhu，Sun Juxiang.Calculation method for ship airbag end launching［J］.Ship ＆ Boat，2009，3:39-44.(in Chinese)

［5］ 余龙，李尧，夏利娟，等.基于超弹性本构模型的船用气囊刚度研究［J］.江苏科技大学学报，2014，28(3):205-210.Yu long，Li Yao，Xia lijuan，et al.Research on stiffness of ship airbag based on hyperelastic constitutive models［J］.Journal of Jiangsu University of Science and Technology，2014，28(3):205-210.(in Chinese)

［6］ 杜杰，船用气囊下水的力学计算及工艺优化［D］.湖北武汉:武汉理工大学，2008:66.

［7］ 张凯敏，船用气囊下水静力学计算与结构分析［D］.浙江杭州:浙江工业大学，2008:102

［8］ 余龙，李尧，夏利娟，等.船用气囊力学特性及极限承载能力研究［J］.上海交通大学学报，2014，48(8):14-19.Yu Long，Li Yao，Xia Lijuan et al.Mechanical property and ultimate nearing capacity of ship airbags［J］.Journal of Shanghai Jiaotong University，2014，48(8):14-19.(in Chinese)

［9］ 成小飞，曹亮.船舶气囊下水工艺中气囊承载性能影响因素分析［J］.港口科技，2012(8):34-37.Chen Xiaofei，Cao Liang.Influential factors analysis for airbag′s bearing capacity in launching process［J］.Science ＆ Technology of Ports，2012(8):34-37.(in Chinese)

［10］ 孙菊香，徐才中，黄立身.70000吨级船舶气囊下水的计算和实践［J］.造船技术，2011，(3):42-45.Sun Juxiang，Xu Caizhong，Hang Lishen.Calculation and practice of the 70 000 ton bulk carrier launching with airbag［J］.Marine Technology，2011，(3):42-45.(in Chinese)