基于扩展卡尔曼滤波的全球导航卫星系统矢量跟踪建模与仿真

曾广裕，申强，李东光，何新

(1.北京理工大学 机电工程与控制国家级重点实验室，北京100081;2.中国兵器工业信息中心，北京100089)

0 引言

全球导航卫星系统(GNSS)卫星定位接收机信号跟踪的目的，是使接收机复制的本地载波及伪码信号与接收到的卫星载波及伪码相位保持一致，以剥离接收信号中的载波及伪码信息［1］。一般卫星定位接收机采取各自独立的跟踪通道，对于不同跟踪通道分别设置有各自独立的载波跟踪及伪码跟踪环，并将各通道获取的伪距及伪距率等观测信息输出给导航解算模块，通过解算伪距方程获取接收机位置、速度等信息，然而，一般接收机设计方案中忽略了卫星与接收机间的运动共性信息，因此也存在接收机动态冗余性能有限，且信号重跟时间长等不足［2］。基于该原则，早在20 世纪80年代，由Spilker 等［2］首次提出了“矢量跟踪”的概念，与此对应的，将一般接收机跟踪环路称为“标量跟踪”。

GNSS 矢量跟踪算法综合了各卫星与接收机位置状态相互关系，通过建立以接收机位置、速度、加速度、钟差及钟漂等误差量为状态量的扩展卡尔曼滤波(EKF)模型，并通过矢量延迟/频率锁定环(VDFLL)完成伪距、伪距率测量及环路控制。文献［3 -6］分析了VDFLL 在弱信号及信号遮挡环境下接收机快速重跟踪性能;文献［7 -10］对比了矢量跟踪算法与标量跟踪算法优缺点，并重点研究了两种不同跟踪算法热噪声特性及对信号检测阈值的改善情况;文献［11 -12］分析了矢量跟踪在抗干扰方面的优势;文献［13］提出了一种基于矢量跟踪算法在异步伪卫星中的应用，不仅克服了伪卫星远近问题，同时提高了接收机定位性能;文献［14］单独对矢量码环VDFLL 跟踪性能进行研究。尽管如此，各文献对矢量VDFLL 跟踪具体滤波跟踪控制过程缺乏详细分析，为此，本文给出了VDFLL 的基本结构与系统模型，对观测量的线性化进行推导;重点分析了VDFLL 滤波跟踪原理，并给出具体时序设计方案，同时针对VDFLL 无法实现对载波相位锁定等问题，提出了一种串联式锁相环(PLL)电文解调模型;最后建立了基于软件接收机的VDFLL 跟踪模型，使用GNSS7700 卫星信号模拟器生成的一组弹丸飞行动态场景数据进行了半实物仿真实验，验证了上述方法的正确性。

1 矢量VDFLL 结构及EKF 模型

1.1 矢量VDFLL 结构

标量接收机基带信号处理过程中，对于不同通道分别设置有独立的载波跟踪环及伪码跟踪环。接收到的卫星信号经射频下变频至中频后，分别与不同通道接收机本地生成的载波频率及伪码相位进行混频，并将混频后积分累加值进行鉴相，获取载波及伪码相位误差信息，也即伪距及伪距率误差等信息，并将获取到的伪距、伪距率残差信息经环路滤波器后转换为本地载波数控振荡器(NCO)及伪码NCO 调整控制量，实现对环路的闭环控制。导航解算过程同样独立于通道处理模型，将获取到的不同通道测量得到的伪距、伪距率等信息，通过解伪距方程方式完成对接收机位置、速度等信息的确定。

VDFLL 综合利用了各通道卫星伪码相位及载波频率等信息，建立以接收机位置、速度、加速度及时钟等信息的EKF 模型，将不同时刻卫星位置状态信息与接收机位置状态信息进行深度融合，VDFLL 算法实现主要基于两个基本原则:首先，伪码相位变化基于接收机位置的改变;其次，载波多普勒频移基于接收机速度的变化［3］。为此，若接收机能获取精确星历信息，精确估算出不同时刻星空卫星运动特性，则通过伪码及载波鉴别器获取得到的伪距及伪距率偏差信息经EKF 后将得到用户的位置、速度、时钟偏移及时钟飘移等参数。图1为基于位置信息的矢量VDFLL 原理框图，其中IP、QP、IE、QE、IL、QL分别代表I、Q 支路即时、超前、滞后通道累加值。

矢量VDFLL 具有与标量接收机相类似的通道处理环节，其不同之处在于，矢量VDFLL 不同通道载波NCO 及伪码NCO 调整控制量生成不再独立，而是通过EKF 估算接收机不同时刻位置、速度等变化规律，接收机位置、速度等信息的变化体现为测量得到信号伪距Δρ、伪距率Δρ·的变化，而伪距及伪距率的改变反映着接收到的伪码相位及载波多普勒的变化。正因如此，矢量接收机跟踪方案有着较标量接收机更多潜在的优势［3］:第一，EKF 能权衡各通道伪码相位及载波频率误差值，通过实时检测不同通道噪声特性，EKF 能提供最优的接收机位置、速度等状态信息，具有更高的动态性能;第二，矢量跟踪过程中，由于综合了各通道卫星信息，接收机能跟踪更为微弱的信号;第三，VDFLL 具有快速重跟踪信号的潜能。

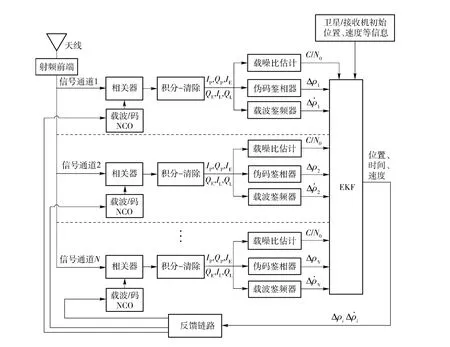
图1 矢量VDFLL 原理框图Fig.1 Schematic diagram of VDFLL

1.2 EKF 状态模型

矢量VDFLL 跟踪算法以接收机位置、速度、加速度、接收机钟差、钟漂等信息为状态量，EKF估计的是状态量误差而非状态量本身，并且用估计的状态量误差信息校正导航输出［7］。定义状态量误差值，其中，前面9 项分别是估计的接收机位置、速度、加速度在地心地固(ECEF)坐标系下的误差值，后两项分别代表估计的接收机钟差及钟漂误差值。状态向量的选取可根据实际应用接收机动态需求选定，对于低动态场景，可忽略接收机自身加速度等信息的干扰，从而降低状态量维数，降低滤波器设计难度。由牛顿运动学规律，系统状态转移方程可表示为

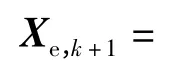
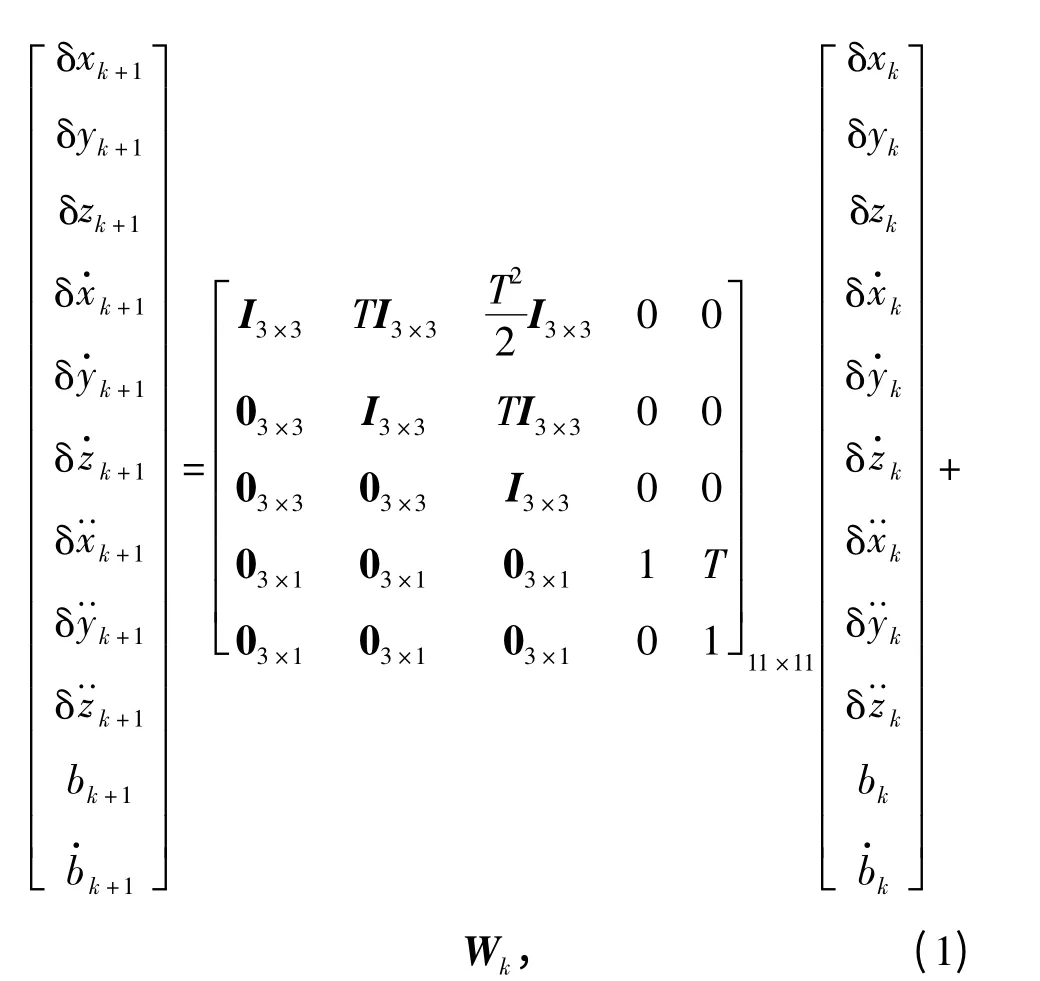
即Xe，k+1=FXe，k+Wk，式中:T 为卡尔曼滤波更新时间;Wk为均值为0，协方差为Q 的过程噪声。

1.3 线性化量测方程

图1所示的矢量VDFLL 设计框图中，每次EKF 更新时刻，不同通道伪码相位及载波频率误差信息将被检测，伪码相位及载波频率误差信息将反映出不同时刻接收机位置、速度、加速度及时钟等信息的变化，且呈非线性关系，分析观测量的线性化过程对理解矢量VDFLL 滤波控制机理具有重要指导意义。

设k 时刻接收机位置、速度可表示为当前时刻估计值加误差值，如(2)式所示:

伪距方程如(3)式所示［1］:

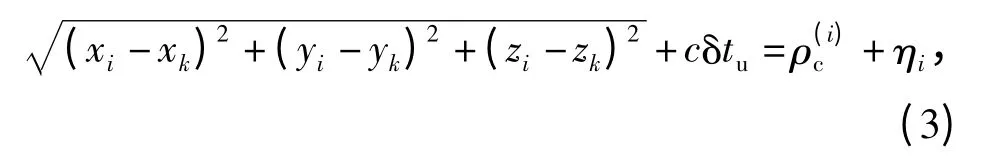
式中:ρ(i)c为修正后i 号星伪距;c 为光速;δtu为接收机时钟误差;ηi为噪声项。

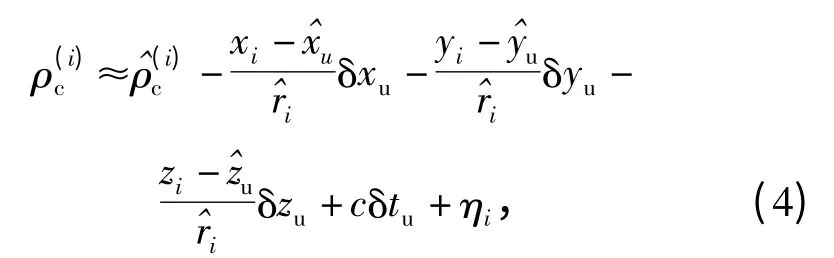
由此，得到伪距残差与状态量关系:

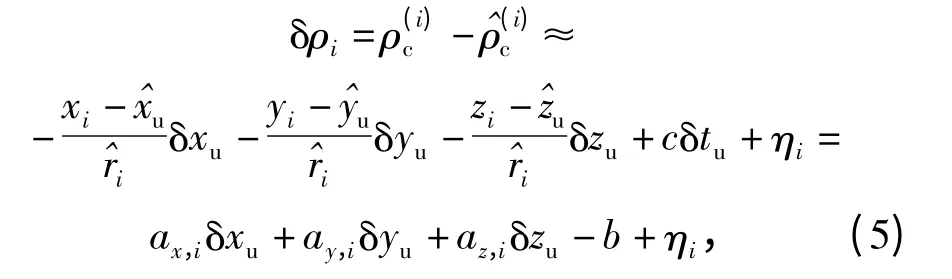
式中:ax，i、ay，i、az，i为接收机相对卫星视线方向LOS 单位矢量。

同样，对于第i 卫星，接收到的信号载波频率fik(单位:Hz)可表示为

式中:fT为信号发射频率;vi为卫星速度;u·k为k 时刻接收机速度;本地时钟偏移;ξi为噪声项。为此，本地接收信号与输入载波频率误差可表示为

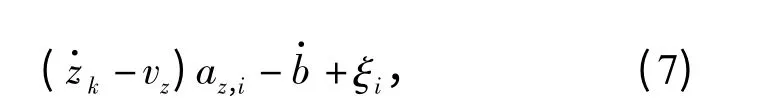
式中:接收到的信号载波频率fik又可表示为k 时刻估计载波频率加频率误差:

将(2)式、(8)式代入(7)式得:

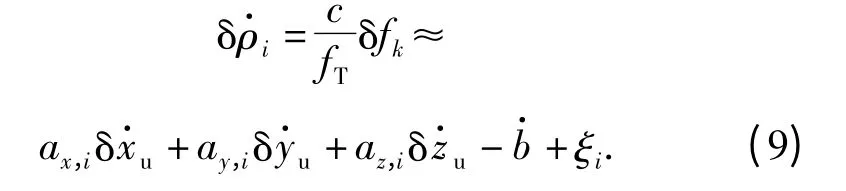
将线性化后的第i 号卫星观测方程(5)式，(9)式写成矩阵形式:

矢量VDFLL 中，最少需同时跟踪4 颗或者4 颗以上通道卫星，基于EKF 算法才能准确估算出不同时刻的状态误差量，为此，对于多通道输入时，量测方程可表示为

式中:Vk为均值为0，协方差为R 的测量高斯白噪声，测量噪声协方差统计值不仅与伪码相位及载波频率鉴别器类型有关，同时也与信号强度有关［9］。文献［9，15］分别介绍了归一化超前减滞后功率法及超前减滞后功率法伪码鉴相策略、四象限反正切及叉积鉴频等不同鉴别器下测量噪声协方差R 的统计求解方法。图2为不同鉴别器测量噪声统计特性随载噪比变化规律。由图2可知，测量噪声协方差R 的大小与载噪比呈近似指数关系变化。由于测量噪声R 中包含了接收机各通道的伪码误差及载波频率误差噪声项，假设各通道的码相位误差以及载波频率误差间不相关，则R 为对角阵，其对角线元素大小与实际接收到的信号强度有关，当卫星信号受到干扰或者遮挡时，实际的噪声项会发生较大的变化，为此，矢量VDFLL 跟踪处理中，为提高接收机抗干扰性能及滤波性能，须实时估算出不同时刻接收信号噪声特性并调整R 的变化［16］。

图2 不同鉴别器测量噪声协方差与载噪比关系Fig.2 Relationship between measurement noise covariance and C/NO of different discriminators

2 矢量VDFLL 滤波跟踪时序分析

矢量跟踪的基本原理是利用码相位和载波频率的预测误差直接修正用户的位置、速度、时间，修正后的用户位置、速度、时间反馈给本地复制信号生成器，生成新的码相位和载波频率的预测值，从而形成闭合的矢量跟踪环路［17］，该算法核心为基于状态量误差的EKF 跟踪控制时序设计。如图3所示，设X为代表接收机位置、速度、加速度、钟差及钟漂等状态向量，Xe为状态量误差向量，其中，位置单位为m，速度单位为m/s，加速度单位为m/s2，接收机钟差及钟漂需转换为位置及速度信息，单位分别为m及m/s. 图3中，下标k 代表第k 次更新历元，代表第k 次更新历元时刻状态量先验及后验估计值。矢量VDFLL 中，每隔Δt 时刻(如20 ms)完成对接收机位置、速度、加速度等参数的预估，并调整NCO，接收机状态估计更新时间t 可大于测量更新时间Δt，通常取20 ms 至1 s 间，具体根据接收机动态应力及噪声特性而定。

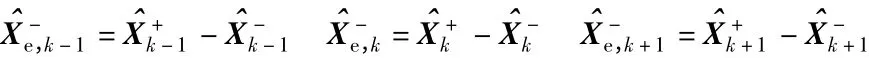
图3 VDFLL 跟踪算法时间更新示意图Fig.3 Time update for VDFLL algorithm

由于EKF 每隔t 时间更新一次状态量，每次EKF 更新后，重新复位状态量误差Xe，k，为此，k +1时刻状态向量误差估计值可表示为

式中:Xk+1为k +1 时刻状态向量真实值为k +1时刻状态向量估计值。

图4为VDFLL 跟踪算法滤波跟踪控制原理框图。矢量VDFLL 跟踪过程中，EKF 是对输入信号与本地生成信号误差偏差量进行滤波，为此，图4中，虚线框内为对状态误差量的EKF 滤波过程，虚线框外为状态量的预测与更新及NCO 调整控制。其中:Zk+1为k+1 时刻接收机接收到的真实伪距及伪距率等参数，为k 时刻本地预估的伪距及伪距率参数;Ze，k+1代表k+1 时刻真实伪距及伪距率与接收机本地生成的伪距、伪距率偏差值，实际应用中，该偏差值由伪码及载波鉴别器获取。

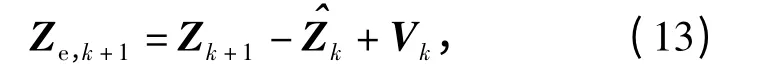
式中:Vk为均值为0，协方差为R 的测量高斯白噪声。

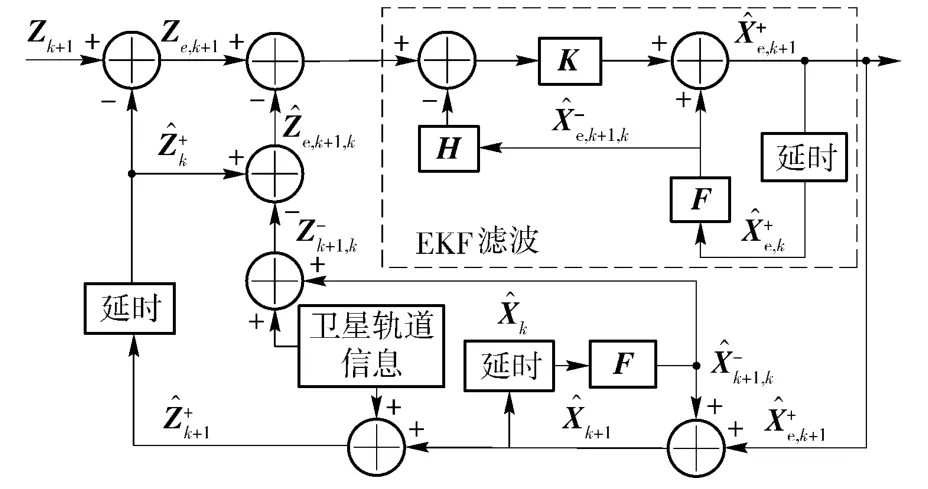
图4 VDFLL 跟踪算法EKF 滤波跟踪控制框图Fig.4 EKF filter control loop of VDFLL tracking

控制过程分两部分:一路为误差状态量的EKF滤波过程;另一部分为状态量更新，状态量更新在每次EKF 循环外进行。具体滤波跟踪控制时序如图5所示。

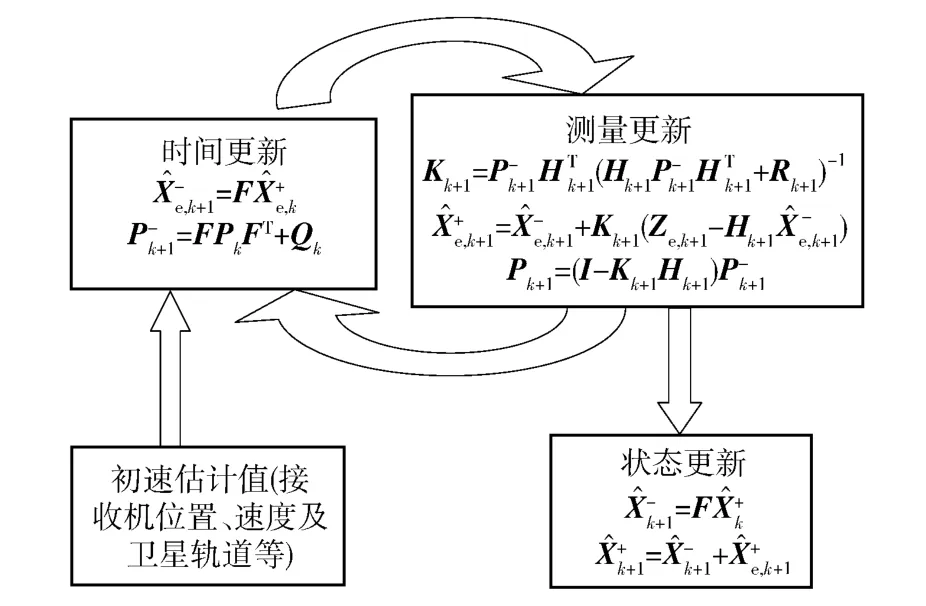
图5 VDFLL 滤波跟踪控制时序图Fig.5 Filter tracking process of VDFLL

矢量VDFLL 跟踪过程中，虽然EKF 滤波过程状态量为接收机位置、速度、加速度及时钟等偏差量，但矢量跟踪前，仍需要获取一定精度的接收机初始位置、速度等信息，否则，若获取到的本地伪码相位与接收信号伪码相位偏差过大(大于半个伪码长度)，将超出伪码鉴别器牵入范围，致使跟踪环路发散。该初始估计值不仅可通过标量接收机引导获取，同时也可以通过外部数据装定等方式实现。

3 串联式PLL 电文解调模型

矢量VDFLL 只通过矢量频率锁定环(VFLL)实现了载波频率的跟踪，但仍无法完成对载波相位的完全解调，为此，单纯的矢量VDFLL 跟踪算法无法实现对导航电文的解调，信号解调过程中，即时支路存在明显的载波相位残差影响。

针对此类问题，结合文献［18］，提出一种基于串联式PLL 电文解调模型，如图6所示。对于不同通道，分别设置有独立的串联式PLL 跟踪环，用以跟踪矢量VDFLL 载波频率残差，该设计方案优点有:1)对于不同通道分别设置有独立的串联式PLL跟踪环，不存在通道间信号串扰现象;2)串联式PLL只跟踪矢量VDFLL 输出的频率残差部分，该模块的正常与否并不影响矢量VDFLL 原有的性能，同时实现了对各通道载波相位的跟踪，完成对导航电文的解调。

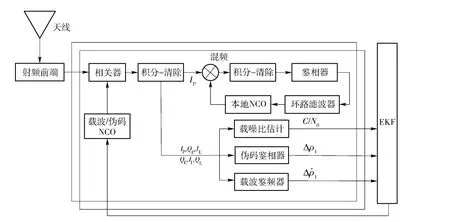
图6 串联式PLL 电文解调模型Fig.6 Series PLL message demodulation model

文献［1］已对此类锁相环参数设计及数字离散过程作了详细描述，不同之处为，本文采取串联式PLL 实现的是对矢量频率跟踪后载波残余频率/相位误差的跟踪，为低频信号，为此，图6中，本地NCO 无须单独增加NCO 偏置，直接利用环路滤波器输出的NCO 调整量即可实现对环路的锁定。

本文提出的串联式PLL 跟踪模块为可选择的，对于矢量VDFLL，载波相位的锁定与否并不影响其对接收机位置状态信息的最优估计，增加串联PLL目的是为了实现对导航电文的正确解调，以弥补矢量跟踪环路本身无法获取导航信息的不足。

4 半实物仿真验证

半实物仿真的目的一方面用以验证所建立的矢量VDFLL 跟踪控制模型的正确性，另一方面分析验证矢量跟踪算法对动态信号跟踪性能。实验数据由GNSS7700 Spirent 模拟器生成一组初速为930 m/s;最大加速度为50 m/s2的弹道飞行场景，如图7所示，各通道卫星信息如表1所示。

图7 实验场景Fig.7 Test scenario

表1 卫星信息Tab.1 Satellite information

矢量跟踪算法以Matlab 软件接收机为平台［19］，将模拟器输出的动态场景卫星信号经NS210B 卫星中频采集器采集并转换为软件接收机可识别的二进制数据源。NS210B 中频采集器输出中频4.1239 MHz，采样频率16.368 MHz. 矢量VDFLL 跟踪前，先经标量跟踪获取矢量VDFLL 相关初始值，如不同卫星信号发射时间、接收机初始位置等信息。矢量VDFLL 跟踪过程中，通过实时解算星历方式获取不同时刻卫星轨道参数。图8为由标量转入VDFLL 跟踪时刻，标量跟踪获取到的星空可视卫星分布效果图，与模拟器生成场景相吻合。仿真过程中，以6 通道VDFLL为例，任意选取6 颗可用卫星，如1、8、9、17、24、28 号卫星，EKF 更新率为20 ms.

矢量VDFLL 跟踪过程中，选取归一化超前减滞后功率法伪码鉴相策略及叉积鉴频策略实现对输入信号与本地生成伪码及载波信号相位与频率偏差估计。测量噪声协方差R 参考文献［9，15］，过程噪声Q 中包含接收机位置、速度、加速度及时钟误差相关

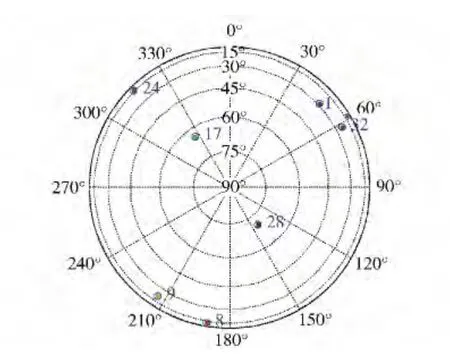
图8 可视卫星分布图Fig.8 Visible satellite distribution

图9 为VDFLL 跟踪24 号星估算得到的伪距、

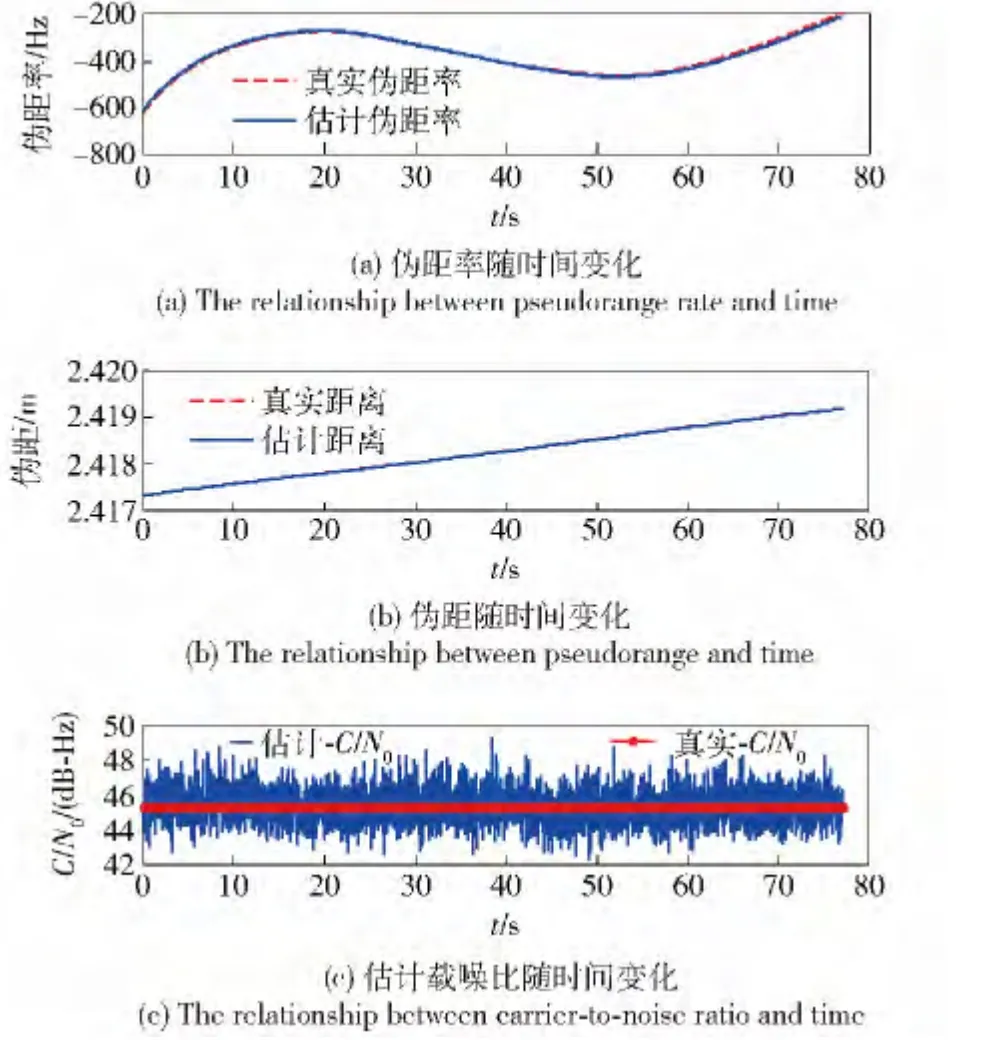
图9 24 号星跟踪效果Fig.9 Tracking result of 24

噪声，这些项可以通过接收机运动状态，本地时钟精度等先验信息进行预设。仿真过程中，Q 设置如下:伪距率及载噪比估计与模拟器真实输出信号对比情况(其余通道类似)。图9(a)～图9(c)分别为:EKF 估算得到的伪距率与模拟器真实输出伪距率对比情况;EKF 估算得到的伪距与模拟器真实输出伪距对比情况;实时载噪比估算与模拟器真实输出载噪比对比情况。由图9可知，矢量VDFLL 跟踪过程中不仅能正确预估出不同时刻卫星相对接收机间伪距及伪距率的变化规律，同时，估算载噪比与模拟器输出基本吻合。

图10 为增加串联式PLL 与否对电文解调效果图。图10 中，图10(a)图为未增加串联PLL 电文解调效果，由此可见，单纯的VDFLL 并不能实现对载波相位的解调，即时支路中存在明显的相位残差;图10(b)为增加串联PLL 后即时支路电文提取效果，对比图10(a)与图10(b)两图可知，矢量VDFLL跟踪过程中，增加串联PLL 能较好地实现对载波残差的锁定，并正确提取出电文信息。

图10 串联式PLL 电文解调效果Fig.10 Result of series PLL message demodulation

图11 和图12 分别为矢量VDFLL 在发射坐标系下检测得到的弹道位置、速度信息及其误差变化规律。发射坐标系定义为以炮位原点为坐标原点O，xf轴在发射点水平面内，并指向目标点，yf轴垂直发射点水平面指向上方，zf轴与Oxfyf平面垂直构成右手坐标系，发射坐标系常用于分析弹丸相对地面的运动情况。由图11、图12 可知，矢量VDFLL 跟踪算法不仅能正确地实现对弹丸飞行位置及速度的实时检测且位置检测均方误差(1σ)为8.5 m，速度检测均方误差(1σ)为0.3 m/s，同时具有良好的动态跟踪特性。

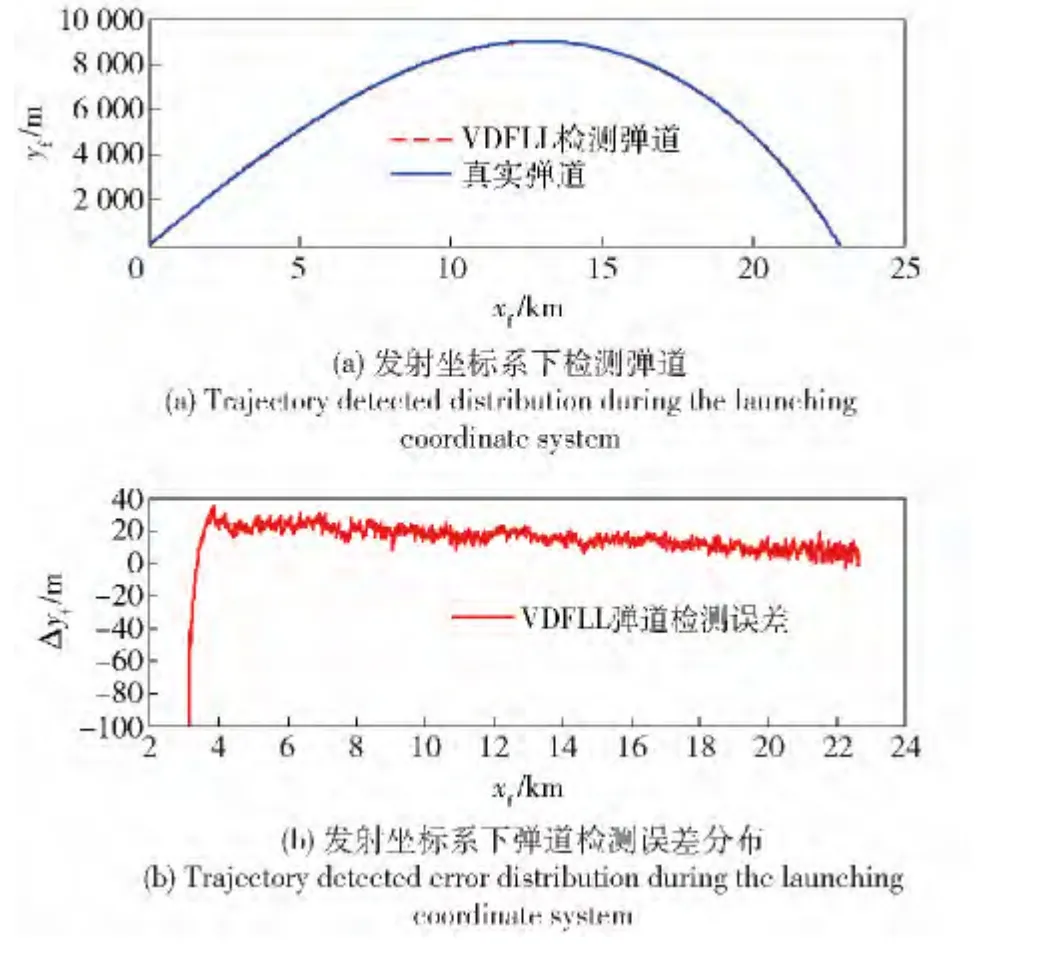
图11 VDFLL 位置估计Fig.11 Position estimation of VDFLL

图12 VDFLL 速度估计Fig.12 Velocity estimation of VDFLL

5 结论

本文研究了基于EKF 的矢量VDFLL 接收机跟踪算法的结构、模型并重点分析了矢量VDFLL 滤波跟踪控制过程;同时针对VDFLL 跟踪算法无法实现对载波相位的锁定，提出一种串联式PLL 电文解调模型;最后建立了以软件接收机为平台VDFLL 跟踪模型，并进行了半实物仿真验证。半实物仿真不仅验证了所建VDFLL 控制模型的正确性，同时进一步验证了矢量跟踪算法具有良好的动态跟踪性能。

References)

［1］Kaplan E. Understanding GPS:principles and application ［M］.Boston，MA:Artech House，1990.

［2］Spilker J J.Vector delay lock loop processing of radiolocation transmitter signals:US 5398034［P］，1995-03-14.

［3］Matthew L，David M.Comparison of traditional tracking loops andvector based tracking loops for weak GPS signals［C］∥ION GNSS 20th International Technical Meeting of the Satellite Division.Fort Worth，TX:Institute of Navigation，2007:789 -795.

［4］Pany T，Eissfeller B. Use of a vector delay lock loop receiverfor GNSS signal power analysis in bad signal conditions［C］∥Proceedings of the IEEE-ION PLANS. San Diego，CA:IEEE，2006:893 -903.

［5］Kanwal N，Hurskainen H，Nurmi J. Vector tracking loop design for degraded signal environment［C］∥Ubiquitous Positioning Indoor Navigationand Location Based Service(UPINLBS)，Kirkkonummi，Finland:IEEE，2010:1 -4.

［6］Kwang-Hoon K，Gyu-In J，Sung-Hyuck I. Adaptive vector-tracking loop for low-quality GPS signals［J］.International Journal of Control，Automation，and Systems，2011，9(4):709 -715.

［7］Matthew L，David M.Vector delay/frequency lock loop implementation and analysis［C］∥International Technical Meeting，Anaheim，California:Institute of Navigation，2009.

［8］Matthew L，David M，Hung J Y.A valid comparison of vector and scalar tracking loops［C］∥Proceedings of IEEE/ION Position，Location and Navigation Symposium Conference. South Carolina，US:IEEE，2010:464 -474

［9］Lashley M，Bevly D M. Analysis of discriminator based vector tracking algorithms［C］∥Proceedings of the 2007 National Technical Meeting of the Institute of Navigation，San Diego，CA:Institute of Navigation，2007:570 -576.

［10］Lashley M，Bevly D M，et al. What are vector tracking loops and what are their benefits and drawbacks［J］. GNSS Solution Column，2006，4:16 -21.

［11］Benson D. Interference benefits of a vector delay lock loop(VDLL)GPS receiver［C］∥Proceedings of the 63rd Annual Meeting of the Institute of Navigation. Cambridge，MA:IEEE/ION，2007:749 -756.

［12］王伟，李强，徐定杰，等.一种矢量跟踪环路及其抗干扰性能分析［J］.电子与信息学报，2013，35(7):1581 -1586.WANG Wei，LI Qiang，XU Ding-jie，et al. Adesign method and anti-jamming performance analysis for vector tracking loop［J］.Journal of Electronics ＆ Information Technology.2013，35(7):1581 -1586.(in Chinese)

［13］So H G，Lee T J，Jeon S H，et al. Implementation of a vector based tracking loop receiver in a pseudolite navigation system［J］. Sensors，2010，10(7):6324 -6346.

［14］Lira D W，Kang H W，Hwang D H，et al.Performance analysis of vector delay lock loop［C］∥ICROS-SICE International Joint Conference. Fukuoka，Japan:IEEE，2009:5046 -5049.

［15］罗雨，王永庆，罗海坤，等. 基于扩展卡尔曼滤波器的矢量跟踪算法研究［J］.电子与信息学报，2013，35(6):1400 -1405.LUO Yu，WANG Yong-qing，LUO Hai-kun，et al.Study on vector tracking loop based on extended Kalman filter［J］. Journal of Electronics ＆ Information Technology，2013，35(6):1400 -1405.(in Chinese)

［16］赵思浩，陆明泉，冯振明.基于自适应卡尔曼滤波的GNSS 矢量锁定环路［J］.哈尔滨工业大学学报，2012，44(7):139 -143.ZHAO Si-hao，LU Ming-quan，FENG Zhen-ming. GNSS vector lock loop based on adaptive Kalman filter［J］. Journal of Harbin Institute of Technology，2012，44(7):139 -143. (in Chinese)

［17］朱珍珍，汤广富，程翥，等.基于矢量延迟锁定环路的GPS 信号跟踪算法［J］.自然科学进展，2009，19(9):1021 -1028.ZHU Zhen-zhen，TANG Guang-fu，CHENG Zhu，et al. EKF based vector delay lock loop algorithm for GPS signal tracking［J］. Progress in Natural Science，2009，19(9):1021 -1028.(in Chinese)

［18］韩孟飞，王永庆，吴嗣亮，等.一种串联结构数字载波环及其Z域噪声性能分析［J］.电子学报，2013，41(2)，307 -313.HAN Meng-fei，WANG Yong-qing，WU Si-liang，et al. A series connection structure digital carrier tracking loop and analysis of its noise performance in Z domain［J］.Acta Electronica Sinnica，2013，41(2):307 -313. (in Chinese)

［19］James Bao-Yen Tsui. Fundamentals of global positioning system receivers:a software approach［M］. 2nd，ed. New York，US:Publishing House of Electronics Industry，2007:193 -217.