主动防御非奇异终端滑模协同制导律

邹昕光，周荻，杜润乐，刘佳琪

(1.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨150001;2.哈尔滨工业大学 航天学院，黑龙江 哈尔滨150001;3.试验物理与计算数学国家级重点实验室，北京100076)

0 引言

先进导弹防御系统的研究和开发给弹道导弹突防带来了严峻的考验。弹道导弹飞行中段处在大气层外，此时推力发动机关闭，弹头和弹体分离，导弹所具有的机动能力很小或者可以忽略不计，导致此阶段弹道导弹的飞行轨迹比较固定，易被导弹防御系统拦截。因此研究有效的防御手段以提高弹道导弹突防成功率具有较大的工程实际意义和理论价值。

目前已经提出了一些提高弹道导弹突防成功概率的方法，例如电子干扰，伪装技术，诱饵技术，使用中制导和末制导，多弹头技术，机动变轨技术等［1］。这些方法本质上都可以归结为被动防御，其出发点都是寻找有效的躲避手段。与此相对，弹道导弹也可以采取主动的防御手段:在受到威胁时释放一个或多个防御导弹来保护自身。防御导弹具有和弹道导弹相同的速度，在距离弹道导弹一定距离的范围内伴飞，采用有效的制导律拦截来袭的拦截导弹［1］。为了叙述简洁清晰，本文后面将突防的弹道导弹称为目标，将导弹防御系统发射的拦截导弹称为拦截导弹，将与弹道导弹伴飞的反拦截导弹称为防御导弹。本文考虑只存在一枚防御导弹的场景。

由于主动防御方式的特点和有效性，该方法在飞机防御中得到了广泛的研究。文献［2］在假设拦截导弹制导律是已知线性制导律的前提下推导了防御导弹和目标的协同制导律。但假设拦截导弹的制导律已知并不符合实际。针对该问题文献［3］提出了一种多模自适应制导律，该制导律通过一组滤波器来确定拦截导弹的制导律和估计制导律参数。但是该方法要求拦截导弹的制导律和制导参数的组合在一个有限的已知集合中选取，而集合的大小受限于滤波器的个数。这限制了该制导律在工程实际中的运用。文献［4］根据防御导弹和目标的不同协同方式(单向协同或者双向协同)设计出了3 种不同的最优主动防御制导律。使用状态方程降阶方法，将高阶运动方程降阶为以零控脱靶量为状态的一阶动态方程，简化了制导律的推导。以上工作都基于最优控制理论，最优制导律的设计需要估计剩余时间参数。而剩余时间参数的估计精度将直接影响制导的精度。拦截导弹一方面需要拦截目标，另一方面需要逃避防御导弹的拦截，这是一个微分对策问题，因此一些文献使用了微分对策理论来研究主动防御问题［5-6］。和最优制导类似，微分对策制导律需要估计终端时刻，而终端时刻的估计精度会直接影响到制导精度。

如果将目标，拦截导弹和防御导弹抽象为空间中的点，那么它们之间的连线构成一个三角形。一种可行的制导策略是防御导弹控制自身处于目标和拦截导弹的视线上且在目标和拦截导弹之间，此时三角形退化为直线，随着拦截导弹不断接近目标最终将撞上防御导弹［7-9］。这种制导策略称为视线三角制导策略，在几何上比较直观。文献［7］提出的制导律采用了视线三角制导策略，制导律的表达式中包含了拦截导弹的加速度项，但在实际中对于防御导弹而言，拦截导弹的加速度是难以获得的量。在文献［8 -9］提出的基于视线三角制导策略的制导律中，防御导弹的制导指令和两个参数成比例。第1 个参数是防御导弹-拦截导弹视线角和拦截导弹-目标视线角的差。第2 个参数是防御导弹和拦截导弹的相对速度。

滑模控制由于对建模误差和外部未知干扰的良好鲁棒性被广泛应用在导弹制导律的设计中［10-22］。文献［13］提出了基于滑模的主动防御协作制导律，研究了大气层内飞机防御导弹攻击的问题。有限时间稳定性理论在1986年被首次提出［14］，由于具备有保障的收敛性时间特性，该理论在制导律设计问题中被广泛使用［15-26］。近年来有限时间收敛滑模控制理论主要用来解决含有角度约束的制导问题，但是一些制导律在被控角度误差很小时会出现奇异问题，导致大的抖振和控制饱和［17-18］。非奇异终端滑模控制方法可以控制滑模变量在有限时间内到达滑模面并且避免由于奇异问题而造成的控制饱和［19-22］。文献［23］和文献［24］针对该问题分别设计了不同的非奇异终端滑模制导律，该制导律在避免奇异问题的同时保持有限时间收敛的特性。

本文试图设计一种大气层外防御导弹高性能的鲁棒制导律。考虑到在制导的大部分时间内目标和防御导弹之间的距离和他们与拦截导弹之间的距离相比是一个小量，将制导分为两个阶段。在第1 阶段对相对运动近似建模，使用基于视线三角制导策略的制导律;第2 阶段考虑到近似建模误差随着时间快速增加，因此使用基于零化视线转率策略的制导律。第2 阶段的制导律使用更加精确的相对运动模型。制导律的设计使用非奇异终端滑模控制理论。本文在理论上证明基于视线三角制导策略可以显著地降低防御导弹的需用过载，而基于零化视线转率的制导律使用更加精确的相对运动模型，因此分阶段的制导方法兼顾了二者的优点。仿真验证了制导律的有效性。

1 问题描述

目标、拦截导弹和防御导弹的相对运动关系如图1所示，其中目标、拦截导弹和防御导弹分别用T、M 和D 来表示。目标、拦截导弹和防御导弹的速度分别用vT、vM和vD表示。拦截导弹-目标的视线角为qεMT和qβMT;防御导弹-拦截导弹的视线角为qεDM和qβDM. OXYZ 为惯性参考系，其中目标和防御导弹的惯性参考系TXTYTZT和DXDYDZD方向和OXYZ 相同，拦截导弹的惯性参考系MXMYMZM方向为坐标系OXYZ 绕OY 轴旋转180°.

图1 目标、拦截导弹和防御导弹相对运动几何关系Fig.1 Interception geometry in three dimensions

拦截导弹-目标和防御导弹-拦截导弹解耦的相对运动方程为

式中:aTqε和aTqβ代表目标加速度在防御导弹-拦截导弹视线系下的纵向平面和侧向平面分量;aDqε和aDqβ代表防御导弹加速度在防御导弹-拦截导弹视线系下的纵向平面和侧向平面分量;aM1qε和aM1qβ代表拦截导弹加速度在拦截导弹-目标视线系下的纵向平面和侧向平面分量;aM2qε和aM2qβ代表拦截导弹加速度在防御导弹-拦截导弹视线系下的纵向平面和侧向平面分量。

2 非奇异终端滑模控制理论

在推导制导律表达式之前先给出制导律采用的有限时间收敛控制理论。

引理1 对于非线性系统

假设存在一个定义在原点邻域U⊂ℝn上的C1光滑函数V(x，t)，并且存在实数γ ＞0 和0 ＜λ ＜1，使得V(x，t)在U 上正定且(x，t)+γVλ(x，t)在U上半负定，则系统是有限时间稳定的［25-26］。

证明见文献［25 -26］，为了简化计算，取V(x，t)=，σ 是滑模变量，取根据引理1，系统有限时间稳定的充分条件有

(6)式为有限时间滑模到达条件。到达时间为

引理2 对于如下2 阶非线性系统

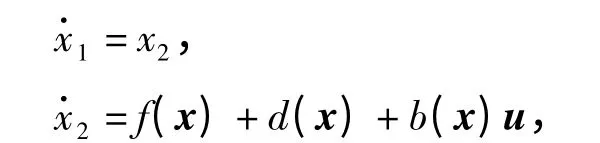
式中:x=［x1，x2］T∈ℝ2. 将其滑模变量设置为σ=x1+，β ＞0，1 ＜α =p/q ＜2，p、q 都是正奇数。引理1 的有限时间收敛条件，可以保证状态x1、在有限时间内收敛到0［19-23］.

状态在时间ts之内收敛到0，ts表达式为

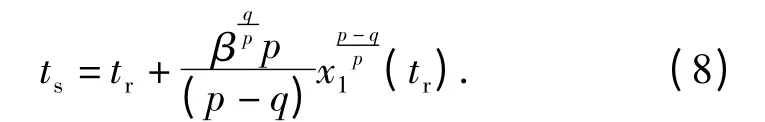
根据引理1，tr是有限正值。由于p、q 都是奇数且p ＞q ＞0，β ＞0，有所以ts≥tr.

3 制导律设计

在防御导弹制导的大多数时间内防御导弹和目标之间距离相对于它们与拦截导弹的距离小得多，而且防御导弹和目标速度矢量十分接近，因此在大部分时间里满足如下关系:

将整个制导分为两个阶段:阶段1 和阶段2. 为了简化制导律的表达式，在阶段1 中认为(9)式和(10)式成立，防御导弹采用视线三角制导策略，保持自身在目标和拦截导弹的视线上，这种制导策略可以有效降低防御导弹的需用过载。在阶段2 中认为(9)式和(10)式不再成立，防御导弹采用零化对拦截导弹视线转率的制导策略。假设防御导弹可以测量相对于拦截导弹的距离RDM和速度，目标可以测量相对于拦截导弹的相对距离RMT和速度并通过通信设备将RMT和发送给防御导弹。防御导弹使用一个门限值μ*来区分这两个阶段。并设

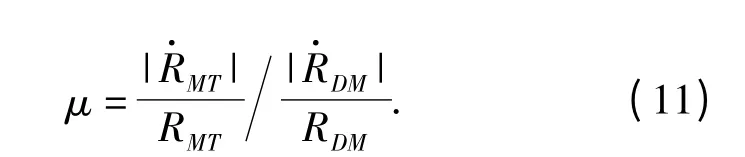
当μ ＞μ*时，防御导弹使用阶段1 制导律，当μ≤μ*防御导弹使用阶段2 制导律。由于防御导弹总是在目标的前下方伴飞，所以0 ＜RDM＜RMT. 当μ*=0 时防御导弹全程使用阶段1 制导律;当μ*=1 时防御导弹全程使用阶段2 制导律。

3.1 阶段1 制导律设计

为了保证防御导弹能击中拦截导弹，防御导弹的制导策略是将自己的位置保持在目标和导弹连线上，同时零化视线转率。即

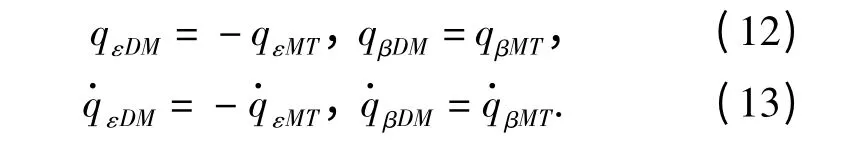
在该阶段中，近似地认为(9)式和(10)式成立。目标在大气层外具有很小的机动能力，本文忽略目标的机动。因此在该阶段中拦截导弹和目标的相对运动方程(1)式和(2)式可以近似为

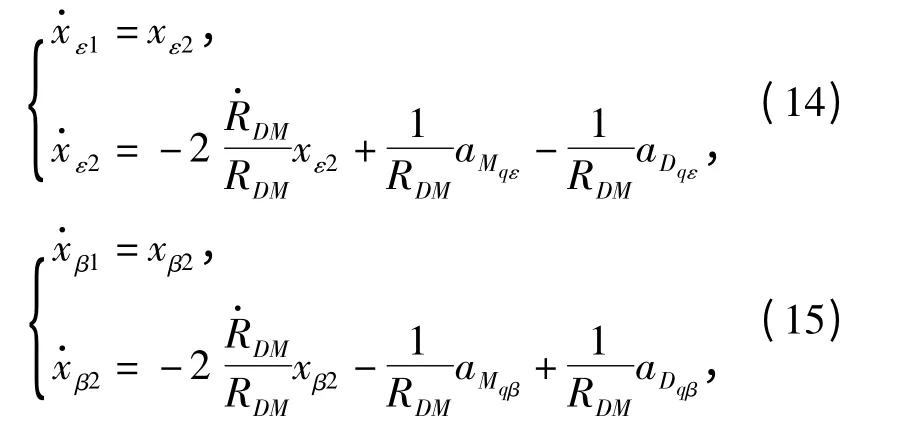
利用非奇异终端滑模设计纵向平面制导律，选取滑动模态面为

式中:β1为常量，β1＞0;1 ＜α1=p1/q1＜2，p1、q1都是正奇数。设计目标是控制aDqε，保证状态xε1和xε2有限时间内趋向0. 对(16)式取时间导数得

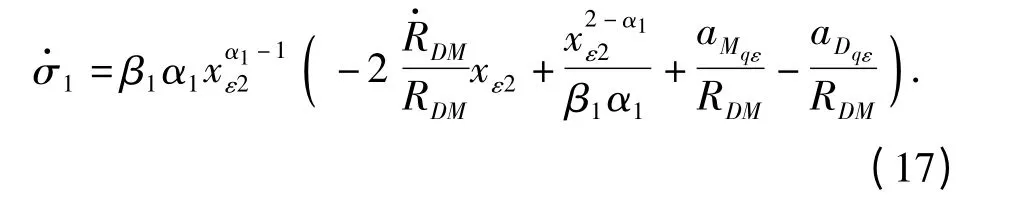
假设防御导弹-拦截导弹和拦截导弹-目标的视线角速率可以分别被防御导弹和目标测量，目标通过通信设备将测量值发送给防御导弹，则xε2可以计算得到。拦截导弹的加速度不能获得但是可以假定拦截导弹的机动能力是有限的。(17)式中拦截导弹加速度aMqε=aM2qε-aM1qε是拦截导弹加速度在防御导弹-拦截导弹视线系和拦截导弹-目标视线系下Y 轴分量的差。按照本制导律设计思路，这两个视线系的Y 轴接近平行且方向相同，因此aM2qε≈aM1qε，因此拦截导弹在(17)式中引入的加速度很小，这是该制导策略的一个优势。假设|aMqε|≤M1，将拦截导弹的机动看成是系统扰动。纵向平面制导律设计为

式中:ρ1=M1+1.

类似的，利用非奇异终端滑模设计侧向平面制导律，选取滑动模态面为

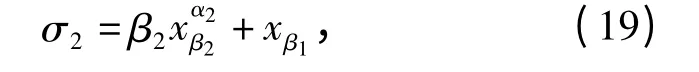
式中:β2为常量都是正奇数。设计目标是控制aDqβ，保证状态xβ1和xβ2有限时间内趋向0. 对(16)式取时间导数得

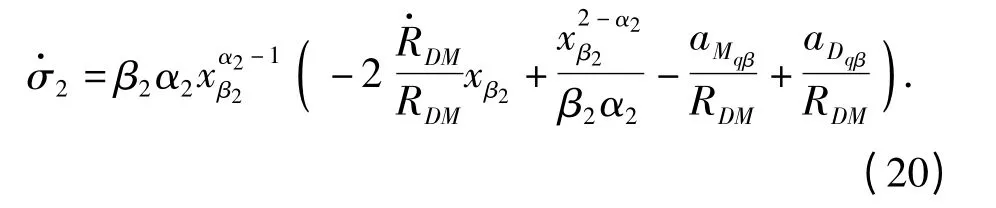
类似地假设防御导弹-拦截导弹和拦截导弹-目标的视线角速率都可以测量，则xβ2可以计算得到;假设防御导弹-拦截导弹的相对距离和相对速度可以测量。拦截导弹的加速度不能获得但是可以假定拦截导弹的机动能力是有限的。(20)式中拦截导弹加速度aMqβ=aM1qβ+aM2qβ是拦截导弹加速度在防御导弹-拦截导弹视线系和拦截导弹-目标视线系下Z 轴分量的和。按照本制导律设计思路，这两个视线系的Z 轴接近平行且方向相反，因此aM2qβ≈-aM1qβ，因此拦截导弹在(20)式中引入的加速度很小。假设|aMqβ|≤M2，将拦截导弹的机动看成是系统扰动。侧向平面制导律设计为

式中:ρ2=M2+1.

定理1 制导系统(14)式和(15)式的制导律分别取(18)式和(21)式时，可以保证状态xε1、、xβ1和在有限时间内趋向0，即防御导弹能够在有限时间内将自身位置调整到目标和拦截导弹的视线上并且保证防御导弹-拦截导弹的视线转率渐进趋向0.

证明 根据(17)式与(18)式有

根据(20)式和(21)式有

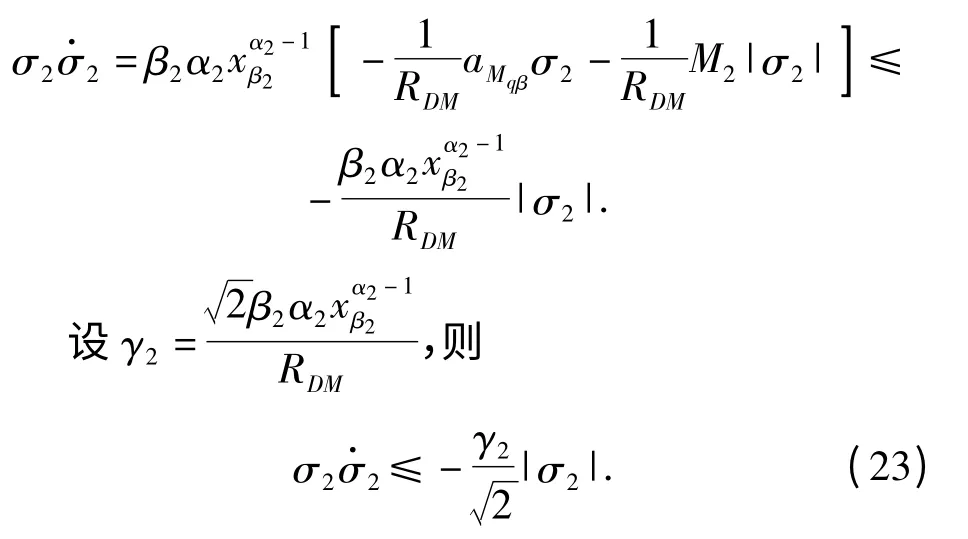
由于σ1和σ2采用了非奇异终端滑模形式，根据引理2 知道xε1、xβ1和在有限时间内收敛到0. 收敛时间分别为

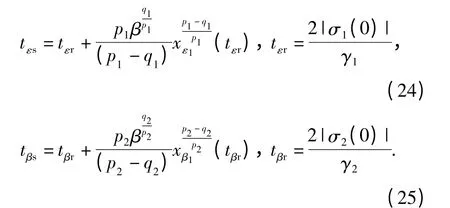
考虑到一般情况下拦截导弹都使用零化视线转率策略的制导律对目标制导，且因为和在有限时间内收敛到0，所以防御导弹对拦截导弹的视线转率会随着收敛到0.

证毕。

3.2 阶段2 制导律设计

在阶段2 中，防御导弹采用零化视线转率的制导策略。此时防御导弹的制导律不再需要考虑目标的运动信息。

利用非奇异终端滑模设计纵向平面制导律，选取滑动模态面为

设计目标是控制aDqε，保证 状 态有限 时 间内趋向0. 对(26)式取时间的导数得

拦截导弹加速度难以测量但是可以假定其是一个有限值，且门限已知，即

和阶段1 的制导策略相比，(27)式中的拦截导弹加速度项不再具有相互抵消的特点，因而这种制导策略下引入的拦截导弹的加速度会比较大。制导律设计为

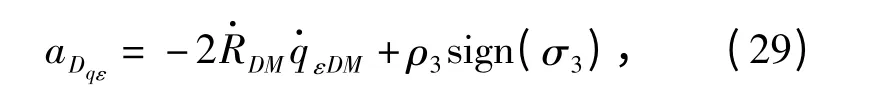
式中:ρ3=M3+1.

类似的，利用非奇异终端滑模设计侧向平面制导律，选取滑动模态面为

设计目标是控制aDqβ，保证状态q·βDM有限时间内趋向0. 对(30)式取时间的导数得

拦截导弹加速度难以测量但是可以假定其是一个有限值，且门限已知，即

制导律设计为

式中:ρ4=M4+1.

定理2 制导系统(3)式和(4)式的制导律分别取(29)式和(33)式时，可以保证防御导弹-拦截导弹的视线转率在有限时间收敛到0.

证明 根据(27)式和(29)式有

设γ3则

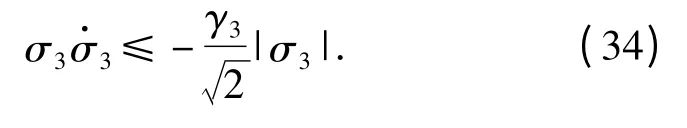
根据(31)式和(33)式有

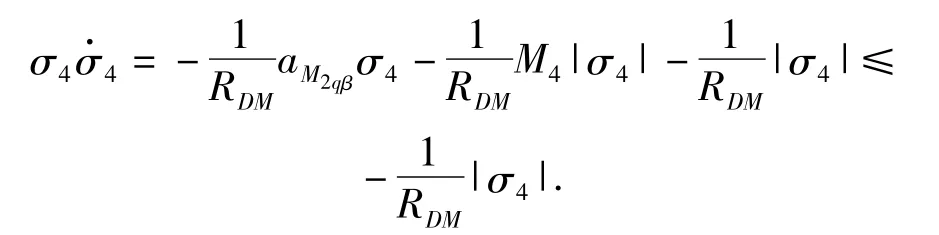
设γ4则

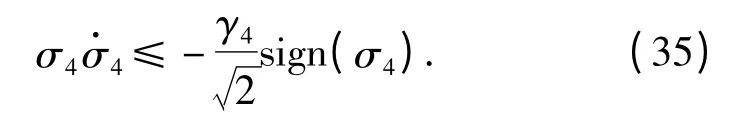
根据引理1 可知滑模变量σ3和σ4在有限时间内达到滑模面。收敛时间分别为

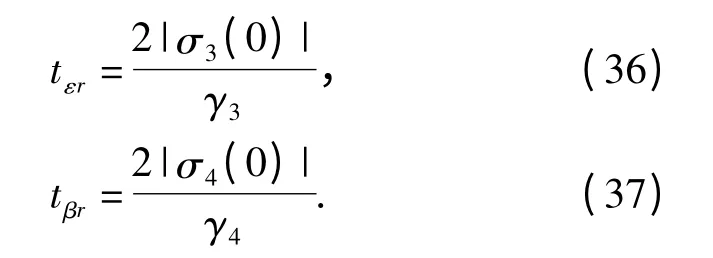
定理得证。

4 仿真结果及分析

在大气层外防御导弹通过轨控发动机产生加速度。而轨控发动机一般是开关式发动机输出的推力只能是固定值或者0，这不适合制导指令是变化的制导律。针对该问题，使用了基于脉冲宽度调制(PWM)的轨控发动机控制方法，基于冲量等效原理，输出可变的等效力，来适应本文设计的制导律。

下面将本文提出的分阶段主动防御非奇异终端滑模制导律简称为AD_NTSM 制导律。为了考察AD_NTSM 制导律的性能，先给出一个仿真算例;接着考察在不同μ*门限值下的制导律性能，以期对于不同的防御导弹机动能力找到对应最佳的μ*值，兼顾两个阶段制导律的优势，发挥最佳性能;最后对比了AD_NTSM 制导律和比例导引(PN)制导律的性能。

在仿真中目标在惯性坐标系下初始位置为(500.0 km，400.0 km，0 km)，拦截导弹在惯性系下初始位置为(559.371 km，319.188 km，0.746 km)，防御导弹在惯性系下的初始位置为(502.903 km，396.206 km，-1.980 km). 目标的初始速度大小为7 071 m/s，初始弹道角为倾角θT0= -35.3°和偏角ψvT0=0°. 拦截导弹初始速度大小为3 000 m/s，初始弹道角为倾角θM0=44°和偏角ψvM0=0°. 防御导弹初始速度大小为7 071 m/s，初始弹道角为倾角θD0=-35°和偏角ψvD0= -2.1°. 目标本身不机动，只受重力作用。拦截导弹和防御导弹的最大加速度均为3 g. 制导律参数选择如下β1=β2=40，M1=M2=20，M3=M4=30，α1=α2=

目标需要通过通信设备将一些制导信息发送给防御导弹。目标和防御导弹虽然速度很快(7 071 m/s)，但是基本上是朝同一方向飞行，大小也大致相同，因此相对速度很小。而且防御导弹会在目标的前下方5 ～7 km 的位置上伴飞，距离也很短。目标和防御导弹之间没有障碍物和大气阻隔，通信条件良好。综上所述制导律对通信设备的要求不高，通信设备比较容易实现小型化。另外由于通信只存在从目标到防御导弹的单向通信，因此弹道导弹上只需要安装发射机，防御导弹上只需要安装接收机。

4.1 仿真算例

在该仿真算例中防御导弹的脱靶量为0.28 m.拦截过程的弹道轨迹如图2所示。从图上看目标和防御导弹的轨迹十分接近，实际上在整个制导阶段中目标和防御导弹的最小距离不小于5.17 km. 这个距离对于目标和防御导弹来说是安全的。

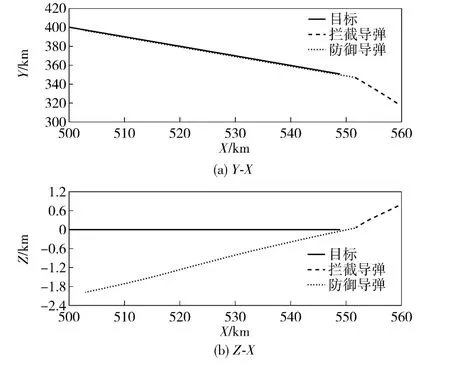
图2 目标、拦截导弹和防御导弹运动轨迹Fig.2 Motion trajectories of target，interceptor and defending missiles

防御导弹加速度在弹体系上的分量如图3所示。前0.5 s 轨控发动机一直处于关闭状态，这是因为前0.5 s 防御导弹和拦截导弹的相对距离超过了防御导弹导引头的最大探测距离(本仿真假设导引头最大探测距离为90 km)。在这段时间内制导律不工作，因此不产生制导指令。

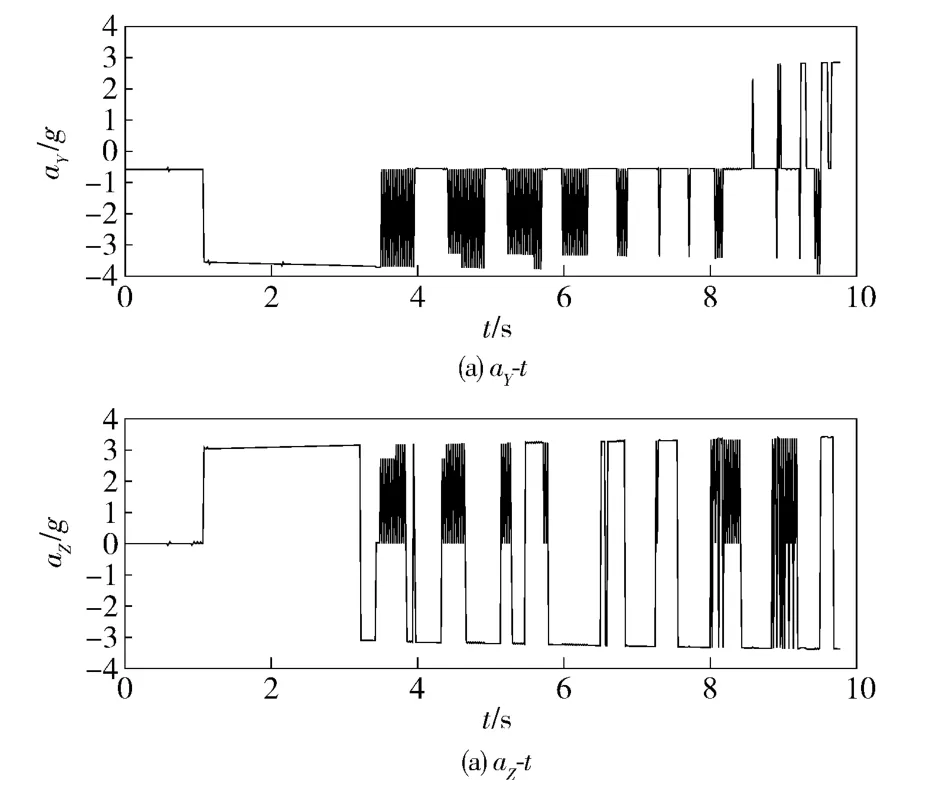
图3 防御导弹发动机推力产生的加速度在弹体系下的分量Fig.3 Lateral accelerations of defending missile in body-axis frame

图4是防御导弹对拦截导弹的视线角速率。在大部分时间内该视线角速率都在［- 0.05°/s，0.05°/s］范围内，随着防御导弹接近拦截导弹，视线角速率逐渐发散。

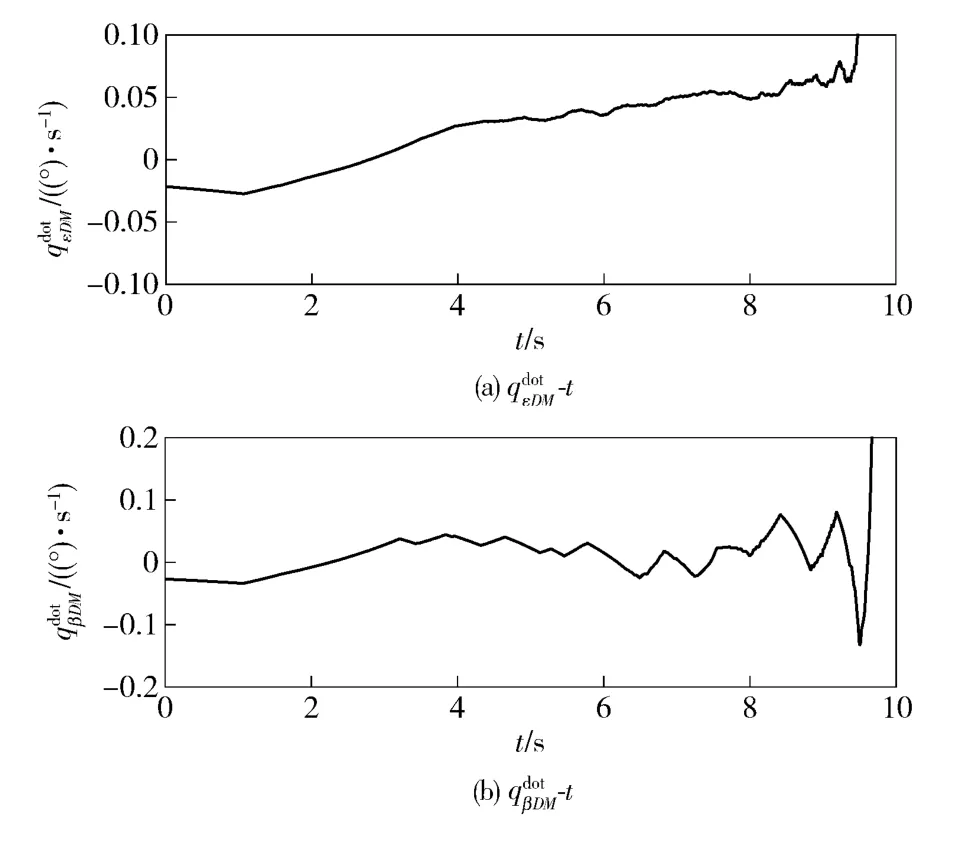
图4 防御导弹-拦截导弹视线角速率Fig.4 Defender-interceptor LOS angular velocities

图5描绘了目标、拦截导弹和防御导弹三点共线的情况。整个制导阶段防御导弹-拦截导弹和拦截导弹-目标视线角之差的范围分别为:视线高低角之差在［0°， - 0.2°］范围内，视线方位角在［-2.2°，-1.5°］范围内，共线情况良好。

图5 目标，拦截导弹和防御导弹三点共线情况Fig.5 Three point collinear of the three bodies

4.2 μ* 对制导律性能的影响

我们考察不同的μ*和不同的防御导弹机动能力下整体制导律的性能。μ*从0 变化到1(代表阶段1 制导律占据的时间越来越短)，步长为0.1. 防御导弹的机动能力从2 g 变化到5 g，步长为0.5 g.图6给出了μ*在防御导弹不同机动能力下对制导性能的影响。

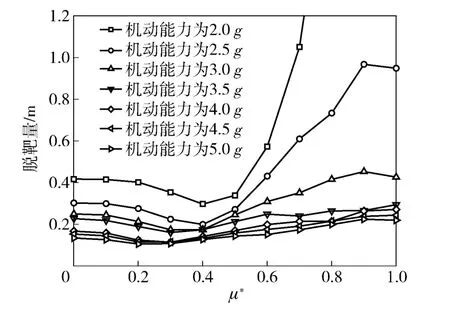
图6 μ* 对制导律性能的影响Fig.6 Choice of μ* for interception phase dividing

从图6可以看出，制导全程使用阶段1 制导律(μ*=0)的效果要比全程使用阶段2 制导律(μ*=1)的效果好。其中原因在阶段1 制导律设计中讨论过，即由于在两个视线坐标系下的拦截导弹的加速度相互抵消而导致引入的加速度很小，利于防御导弹的拦截。这说明了视线三角制导策略的优势。在μ*较小时，制导性能随着μ*增加而提高;而当μ*较大时，制导性能随着μ*增加而下降。这是因为在μ*较小时，在制导后期仍旧使用阶段1 制导律，此时近似相对运动建模误差快速变大，阶段1 制导律性能下降。如果及时采用精确建模的阶段2 制导律，总体制导性能会提高。随着μ*继续增大，阶段2 制导律越来越早使用。当μ*增加到一定程度(例如对于防御导弹机动能力为2.0 g 或2.5 g 时，μ*=0.4;防御导弹机动能力为3.0 g 或3.5 g 时，μ*=0.3)，制导性能进入拐点，继续增加μ*会造成阶段1 制导律使用的时间过短，其制导优势难以充分体现，从而导致总体制导性能开始下降。

4.3 AD_NTSM 制导律和PN 制导律比较

为了横向比较AD_NTSM 制导律的性能，考察了在相同的防御导弹机动能力下，AD_NTSM 制导律和PN 制导律的性能。碰撞杀伤场景需要的脱靶量很小，一般要求在0.3 ～0.5 m 之间，因此比较了AD_NTSM 制导律和PN 制导律脱靶量小于0.3 m和小于0.5 的概率以及平均脱靶量这3 个统计指标。仿真考察了防御导弹机动能力从2.0 g 变化到5.0 g，步长为0.5 g 的7 种不同情况下，每种情况针对AD_NTSM 制导律和PN 制导律分别进行了200 次Monte Carlo 仿真。

AD_NTSM 制导律门限值取μ*=0.4. 其余仿真参数和仿真算例的设置一样。在Monte Carlo 仿真中拦截导弹和防御导弹的初始位置都分别加上了一个均匀分布的随机向量。这两个随机向量的2 范数的平均值分别为3.5 km 和5.0 km.

仿真结果如表1所示。从表1中可以看出，在相同机动能力下，AD_NTSM 制导律性能优于PN 制导律。这是因为AD_NTSM 制导律含有可以抵消拦截导弹机动影响的变结构项。特别的，当防御导弹机动能力较小时，AD_NTSM 性能显著优于PN 制导律。除了上面的原因之外，还因为采用视线三角制导策略的AD_NTSM 制导律在阶段1 制导中当防御导弹-拦截导弹视线系和拦截导弹-目标视线系接近平行时(即目标，拦截导弹和防御导弹三者接近共线时)，拦截导弹在两个视线系下的加速度会互相抵消，导致引入到(17)式和(20)式中的拦截导弹加速度很小。由于制导律将拦截导弹的加速度当做外部干扰处理，小的外部干扰有利于降低防御导弹需用过载。

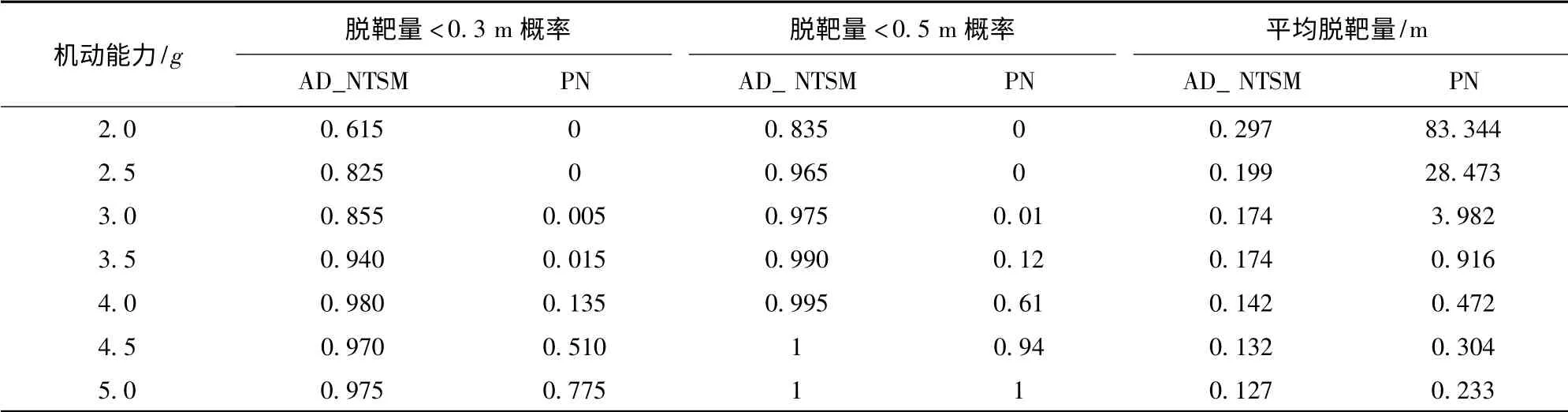
表1 AD_NTSM 制导律和PN 制导律性能比较Tab.1 Comparison of performances of AD_NTSM and PN guidance laws

5 结论

本文研究了大气层外弹道导弹突防的主动防御制导问题。将制导过程分为两个阶段。阶段1 设计了基于视线三角制导策略的制导律，防御导弹控制自身位置处于目标和拦截导弹的视线上。本文首次在理论上证明了该阶段制导律能有效地降低防御导弹的需用过载。由于采用近似相对运动模型，简化了制导律的表达形式。但是在阶段2 中近似建模误差随时间快速增大，因此设计了基于零化视线转率的制导律，使用更为精确的相对运动模型。两阶段制导律均使用非奇异终端滑模控制方法设计，保证防御导弹在有限时间内可以将自身调整到目标和拦截导弹的视线上并零化对拦截导弹的视线转率。最后进行了数值仿真，结果表明在整个制导阶段防御导弹在较高的精度上达到了上述2 个目标:1)保持在目标和拦截导弹的视线上;2)对拦截导弹的视线角速率控制趋于0. 和PN 律进行对比可以看到，所提制导律在达到同样的脱靶量精度情况下，需用过载更小。

References)

［1］冯小荣，樊秋林. 对外大气层动能杀伤拦截器EKV 的突防方法研究［J］. 红外与激光工程，2006，35(增刊1):52 -55.FENG Xiao-rong，FAN Qiu-Lin. Research on ballistic missile exoatmospheric penertration against EKV［J］. Infrared and Laser Engineering，2006，35(S1):52 -55. (in Chinese)

［2］Shima T. Optimal cooperative pursuit and evasion strategies against a homing missile［J］. Journal of Guidance，Control，and Dynamics，2011，34(2):414 -425.

［3］Shaferman V，Shima T. Cooperative multiple-model adaptive guidance for an aircraft defending missile［J］. Journal of Guidance，Control，and Dynamics，2010，33(6):1801 -1813.

［4］Prokopov O，Shima T. Linear quadratic optimal cooperative strategies for active aircraft protection［J］. Journal of Guidance，Control，and Dynamics，2013，36(3):753 -764.

［5］Rubinsky S，Gutman S. Three-player pursuit and evasion conflict［J］. Journal of Guidance Control and Dynamics，2014，37(1):98 -110.

［6］Perelman A，Shima T，Rusnak I. Cooperative differential games strategies for active aircraft protection from a homing missile［J］.Journal of Guidance，Control，and Dynamics，2011，34(3):761 -773.

［7］Ratnoo A，Shima T. Line-of-sight interceptor guidance for defending an aircraft［J］. Journal of Guidance，Control，and Dynamics，2011，34(2):522 -532.

［8］Yamasaki T，Balakrishnan S N，Takano H. Geometrical approachbased defense-missile intercept guidance for aircraft protection against missile attack［J］. Journal of Aerospace Engineering，2012，226(8):1014 -1028.

［9］叶继坤，雷虎民，李炯，等. 基于角度关系的几何制导律研究［J］. 系统工程与电子技术，2011，33(12):2721 -2725.YE Ji-kun，LEI Hu-min，LI Jiong，et al. Research on geometric guidance law based on angle relation［J］. Systems Engineering and Electronics，2011，33(12):2721 -2725. (in Chinese)

［10］Brierly S D，Longchamp R. Application of sliding mode control to air-air interception problem［J］. IEEE Transactions on Aerospace and Electronic Systems，1990，26(2):306 -325.

［11］Zhou D，Mu C D，Xu W L. Adaptive sliding-mode guidance of a homing missile［J］. Journal of Guidance，Control，and Dynamics，1999，22(4):589 -594.

［12］Moon J，Kim K，Kim Y. Design of missile guidance law via variable structure control［J］. Journal of Guidance，Control，and Dynamics，2001，24(4):659 -664.

［13］花文华，陈兴林，宋超. 主动防御协同自适应滑模制导律［J］. 飞行力学，2012，30(1):66 -70.HUA Wen-hua，CHEN Xing-lin，SONG Chao.Cooperative guidance law for active protection based on adaptive sliding-mode control［J］. Flight Dynamics，2012，30(1):66 -70. (in Chinese)

［14］Haimo V T. Finite time controllers SIAM［J］. Journal on Control and Optimization，1986，24(4):760 -770.

［15］Zhou D，Sun S，Teo K L. Guidance Laws with finite time convergence［J］. Journal of Guidance，Control，and Dynamics，2009，32(6):1838 -1846.

［16］Zhou D，Qu P P，Sun S. A guidance law with terminal impact angle constraint accounting for missile autopilot［J］. Journal of Dynamic Systems，Measurement，and Control，2013，135(5):051009.

［17］Kumar S R，Rao S，Ghose D. Sliding mode guidance and control for all-aspect interceptor with terminal angle constraints［J］.Journal of Guidance，Control，and Dynamics，2012，35(4):1230 -1246.

［18］Zhang Y，Sun M，Chen Z. Finite-time convergent guidance law with impact angle constraint based on sliding-mode control［J］.Nonlinear Dynamics，2012，70(1):619 -625.

［19］Feng Y，Yu X，Han F L. On nonsingular terminal sliding-mode control of nonlinear systems［J］. Automatica，2013，49(6):1715 -1722.

［20］Yu S H，Yu X H，Shirinzadeh B，et al. Continuous finite-time control for robotic manipulators with terminal sliding mode［J］.Automatica，2005，41(11):1957 -1964.

［21］Khoo S Y，Xie L H，Man Z H. Robust finite-time consensus tracking algorithm for multirobot systems［J］. IEEE ASME Transactions on Mechatronics，2009，14(2):219 -228.

［22］冯勇，鲍晟，余星火. 非奇异终端滑模控制系统的设计方法［J］. 控制与决策，2002，17(2):194 -198.FENG Yong，BAO Sheng，YU Xing-huo. Design method of nonsingular terminal sliding mode control systems［J］. Control and Decision，2002，17(2):194 -198.(in Chinese)

［23］Kumar S R，Rao S，Ghose D. Nonsingular terminal sliding mode guidance with impact angle constraints［J］. Journal of Guidance，Control，and Dynamics，2014，37(4):1 -17.

［24］Wang X，Wang J. Partial integrated missile guidance and control with finite time convergence［J］. Journal of Guidance，Control，and Dynamics，2013，36(5):1399 -1409.

［25］孙胜. 有限时间收敛寻的导引律［D］. 哈尔滨:哈尔滨工业大学，2010.SUN Sheng. Guidance laws with finite time convergence for homing missiles［D］. Harbin:Harbin Institute of Technology，2010.(in Chinese)

［26］Bhat S P，Bernstein D S. Finite-time stability of continuous autonomous systems［J］. SIAM Journal on Control and Optimization，2000，38(3):751 -766.