随动推力作用下柔性自旋飞行器横向振动响应及失稳分析

荣吉利，徐天富，王玺，殷新喆

(1.北京理工大学宇航学院，北京100081;2. 北京航天发射技术研究所，北京100076)

0 引言

现代火箭或导弹等空间飞行器通常选取较高的推重比，结构长径比设计也越来越大，其目的是为了提高飞行速度及增加有效射程。但这同时也带来不利影响，导致弹箭结构的弹性效应愈加明显，柔性飞行器的结构振动特性和动力学稳定性问题逐渐得到学者们的关注。

Chae 等［1］考虑了多种因素对细长柔性飞行器进行了动力分析以及气动分析，得到了临界推力作用下的发散响应结果。Trikha 等［2］采用两种方法推导了柔性空间飞行器的一般运动方程，其分析结果表明速度、加速度、随动推力等因素对结构稳定性产生重要影响。文献［3 -4］提出了大长径比弹箭柔性弯曲的动力学模型和有限元模型，并研究了弹箭飞行过程中的共振不稳定性问题，得出柔性变形使弹箭的飞行稳定性变坏的结论。许赟等［5］建立了随动推力作用下的非均匀梁振动分析数学模型，通过数值仿真表明随动推力会诱发弹箭飞行器的动力学失稳，同时影响结构的振动频率和振型特性。张雷等［6］引入气动耦合项对有推力的细长导弹的横向弯曲振动进行了数学建模，其分析结果表明气动弹性使得结构稳定性降低。以上这些研究都是针对非自旋类柔性飞行器的，都没有考虑飞行器自旋的作用。

何斌等［7］采用柔体浮动框架和气动弹性小参数摄动法建立了柔性旋转弹箭飞行力学模型，给出了被动段时系统临界状态的条件和临界转速。Zhu等［8］考察了变推力作用下系统质量偏心因素对自旋飞行器系统动力特性的影响，其仿真结果表明结构振动规律与变推力频率密切相关。目前以柔性自旋飞行器为对象考虑随动推力作用的研究还较少。本文在前人工作的基础上，着重考虑飞行器的自身旋转和随动推力的共同作用，对飞行器横向振动响应及失稳情况进行分析。

本文采用剪切变形对轴向位移有贡献的Timoshenko 梁模型，基于有限元方法建立计入陀螺力矩及随动推力影响的系统运动方程，通过数值仿真分析了一定转速时随动推力作用下系统的横向振动响应及结构失稳情况。

1 动能、势能和外力功

1.1 动能和势能

柔性自旋飞行器的简化模型如图1所示，图中Oxyz 为准弹体坐标系，弹体以角速度Ω 绕x 轴自旋;随体坐标系O'ξηζ 固连在轴段微元形心上，跟随弹体微元一起转动。如图2所示，由两坐标系之间的转换关系，轴段微元角速度在随体坐标系下的分量可表示为

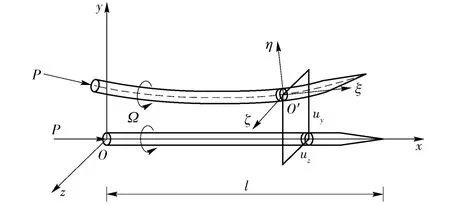
图1 弹体模型Fig.1 Model of flight vehicle

图2 坐标系转换关系Fig.2 The transformational relation between the coordinate systems

忽略弹体的轴向变形，即假设结构无纵向伸缩，但是考虑弯曲和剪切作用对轴向变形的影响。系统动能为

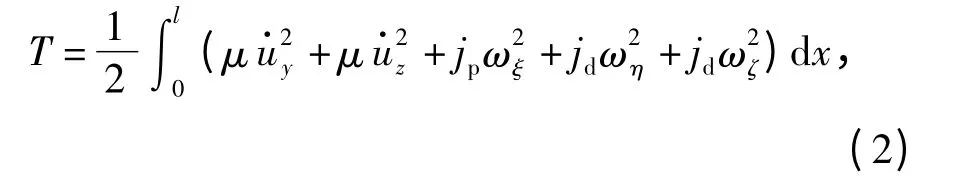
式中:uy、uz分别为梁截面y 向、z 向的横向位移;μ、jd和jp分别为单位长度的质量密度、直径转动惯量和极转动惯量;l 为弹体长度。

当弹体弹性变形较小时，可取近似关系cos θη'≈1和sin θη'≈θη'≈θy，略去高阶小量，得到简化动能表达式

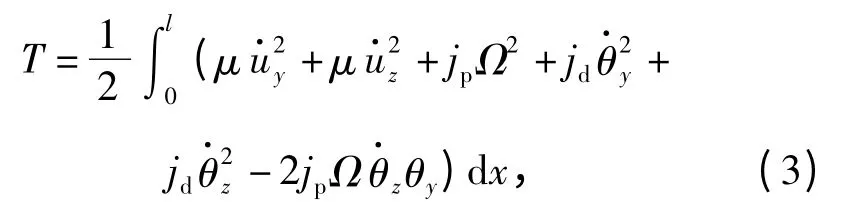
式中:θy、θz分别为该截面的转角;-2jpΩθ·zθy为耦合项，是由陀螺力矩作用引起的。

考虑剪切变形的影响，系统的弹性势能为

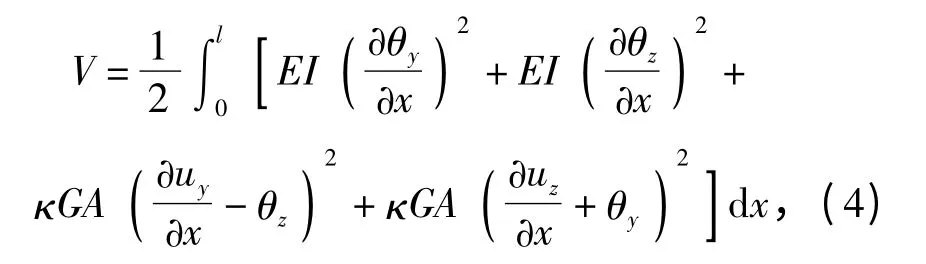
式中:EI 和κGA 分别为弯曲刚度和剪切刚度。

1.2 外力功

考虑剪切变形后，其将与横向弯曲位移共同对轴向位移产生影响［9］，图3所示为Oxy 平面内在剪切力Fsy作用下微元的轴向位移示意图，由图中关系可得Oxy 平面内的轴向位移

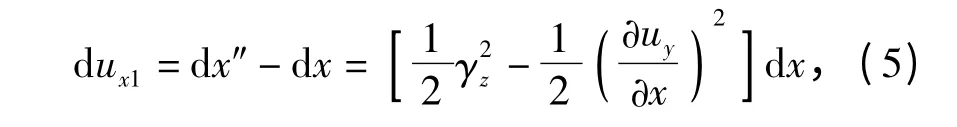
同样地，得到Oyz 平面内的轴向位移

式中:γy为微元中心轴线绕y 轴的剪切角。

忽略气动力作用，将推力P 视为定常随动推力，在推力和惯性力作用下得到轴向力分布表达式

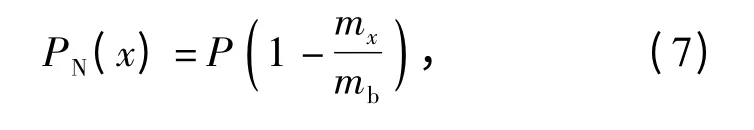
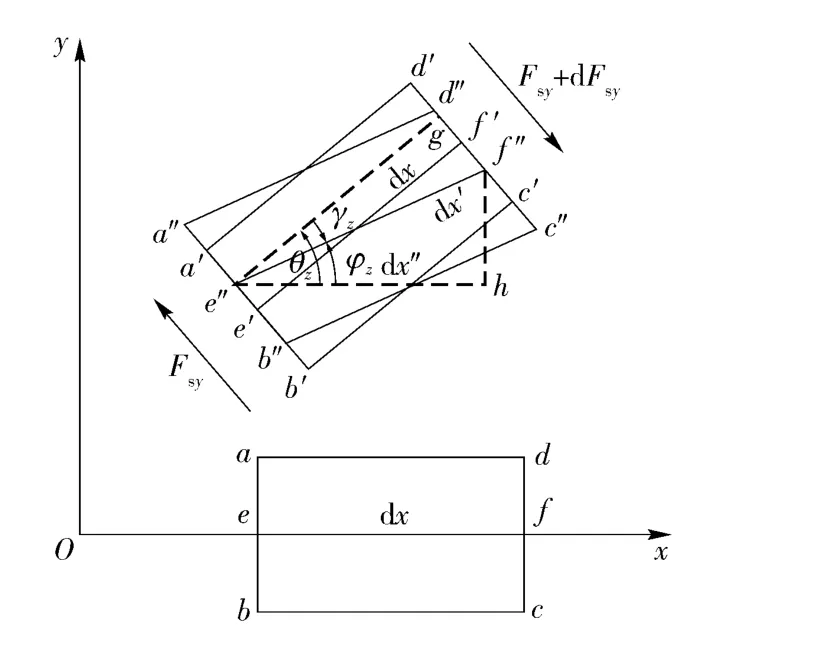
图3 Timoshenko 梁的轴向位移Fig.3 Axial displacement of Timoshenko beam

所以随动推力保守部分所做功为

在弹体尾部，随动推力非保守部分所做虚功为

2 运动方程

按有限元方法的思想，将弹体模型沿轴向进行离散，整体划分为n 个梁单元。为了便于分析，每个梁单元近似为等截面梁。将整体坐标系转换到单元局部坐标系下，采用Timoshenko 梁单元对其横向位移和转角进行插值，得

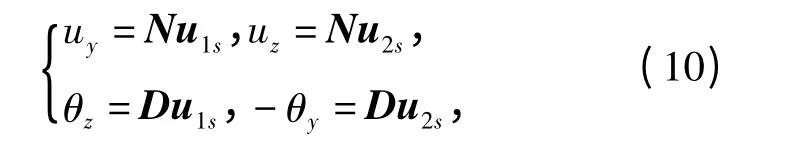
式中:N 和D 分别为位移和转角插值函数矩阵;u1s和u2s分别为y 向和z 向的广义坐标［10］。

离散化后第i 个单元的轴向力可表示为

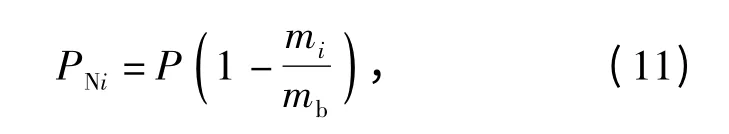
式中:

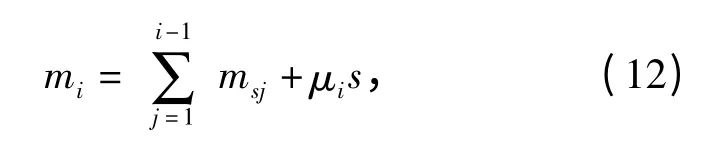
其中msj为第j 个单元的质量，j =1，2，…，i -1，μi为第i 个单元的线密度，s 为单元局部坐标。

非保守系统的Lagrange 方程表达为

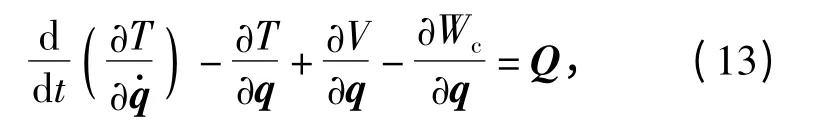
式中:q 和Q 分别为广义坐标和包括非保守力在内的广义力。取q 分别为u1s和u2s，由此得到单元的运动方程

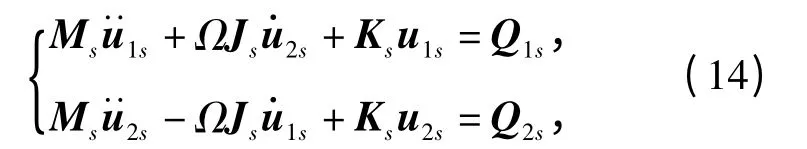
式中:Ms、ΩJs和Ks分别为单元的质量矩阵、回转矩阵和刚度矩阵，此时广义力Q1s和Q2s为不包括随动推力在内的广义力。单元刚度矩阵包含了随动推力的影响，Ks=Kes-Kcs-Kncs，Kes为单元弹性刚度矩阵，Kcs为由推力保守部分得到的单元刚度矩阵，Kncs为由推力非保守部分得到的单元刚度矩阵。单元矩阵Ms、Js和Kes的具体表述请参考文献［10］，这里只给出单元矩阵Kcs和Kncs的表述:

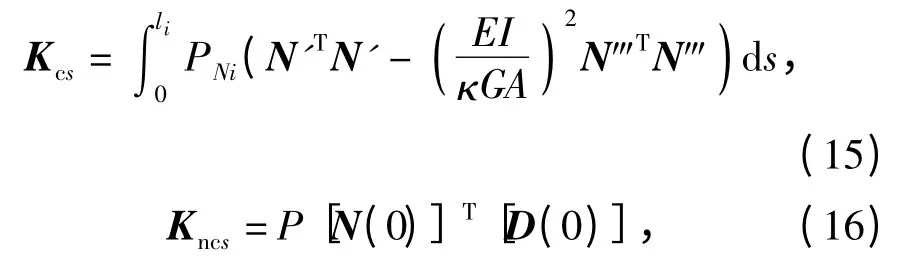
式中:li为单元长度。注意，(16)式表述的Kncs只作用在随动推力所施加的单元上，在其他单元的刚度矩阵中Kncs元素皆为0.

考虑阻尼影响，利用有限元方法，可以得到柔性自旋飞行器运动方程的一般形式，即

式中:M、C、G 和K 分别为系统的质量矩阵、阻尼矩阵、回转矩阵和刚度矩阵;Q 为作用在弹体上载荷列阵。陀螺力矩的作用使得回转矩阵G 为反对称矩阵，而随动推力的作用使得刚度矩阵K 为非对称矩阵。最后施加平均弹轴条件［3］，对自由边界的弹体变形进行约束。

3 数值仿真及结果分析

根据前文得到的细长自旋飞行器系统的运动方程，采用Newmark 方法进行求解，编制了相应的仿真程序，对在推力和自旋作用下的弹体振动情况进行仿真分析。

以长径比为25 的等截面细长回转梁作为弹体仿真模型，整体分为4 段，相关参数见表1. 在不同条件下对此模型分别进行临界转速［10-11］和临界推力分析［12］，结果分别见表2和表3. 表2中:无量纲推力=P/Pcr0，Pcr0为Ω=0 时系统的临界推力，Pcr0=9.84 ×106N;无量纲临界转速= ωcr/ωcr0. 表3中:无量纲临界推力=Pcr/Pcr0;无量纲转速=Ω/ωcr0，ωcr0为P =0 时系统的一阶临界转速，ωcr0=97.16 rad/s. 可见，不同条件下系统的临界转速和临界推力是不同的。

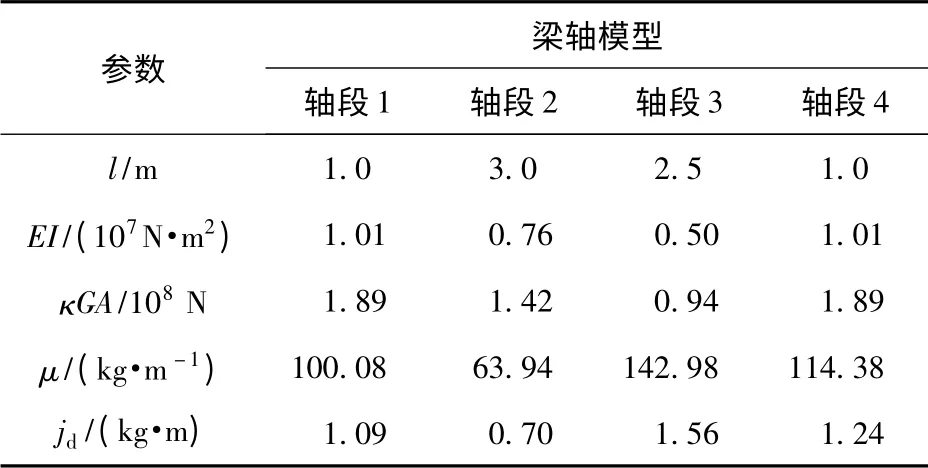
表1 梁轴模型参数Tab.1 Parameters of beam model

表2 临界转速Tab.2 Critical speed

表3 临界推力Tab.3 Critical thrust

分析由质量偏心因素引起的弹箭结构横向振动响应问题，把偏心力作为弹体结构的激振力施加于弹体质心位置处，设偏心距为e =1 mm，激振力频率与自转频率相同，即计算转速分别为0.5、1.0、1.5 时和推力分别为0、0.1 时系统质心的横向位移响应情况，结果如图4所示。

由于随动推力的作用，使得弹体结构的弯曲和剪切变形对轴向位移产生影响，进而减小了系统刚度，所以推力的增加会使结构的振动响应幅值增大。由图4(a)可见，仿真结果与理论相符。图4(b)中结果显示，曲线1 和曲线3 两种情况表明系统发生共振，结构变形发散，因为它们的转速均达到了各自状况下的临界转速(见表2)。图4(b)中曲线2 情况表明结构产生拍振现象，原因是随动推力的增加降低了系统的临界转速，使此时的转速避开了本状况下的临界转速，因此也避免了共振的发生。对应于图4(b)中曲线1、曲线3 两种情况，图5显示了弹体质心横向位移在临界转速下的共振发散轨迹。对比图4(a)和图4(c)，在相同推力作用下，转速的增加使质量偏心力增大，从而使得相应的振动响应幅值增大。

图4 不同条件下系统质心的位移响应Fig.4 Displacement responses of mass center under different conditions

图5 弹体质心轨迹Fig.5 Trace of mass center of flight vehicle

现考察推力接近或超过临界推力时弹体结构的响应问题。图6显示了P=1.00 时在不同转速下系统的位移响应，明显发现此时不论转速如何系统都将产生失稳。因为弹体自旋在一定程度上降低了系统的临界推力，使得此时的推力Pcr0大于任何转速下的临界推力(见表3)，所以不论转速如何最终都将导致系统失稳。图7显示了弹体颤振失稳时质心的发散轨迹。事实上，当推力达到临界推力值后，由于结构振动失稳，图6和图7中的情况会造成系统结构的破坏，而实际位移不会如此之大。取推力=0.76，不同转速下的系统质心位移响应如图8所示。对于图8中曲线1、曲线2 两种情况，推力均未达到各自状况下的临界推力(见表3)，所以振动响应曲线稳定;对于曲线3 情况，由于弹体自旋作用使得此时的临界推力值降幅很大(见表3)，推力已达到临界推力值，所以结构发生颤振失稳。

图6 临界推力作用下系统质心的位移响应Fig.6 Displacement response of mass center under critical follower thrust

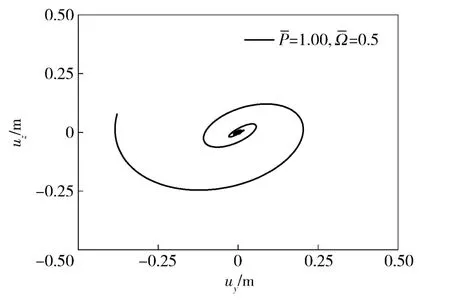
图7 弹体质心轨迹Fig.7 Trace of mass center of flight vehicle

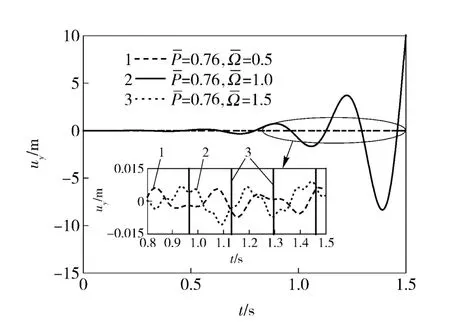
图8 不同转速下系统质心的位移响应Fig.8 Displacement responses of mass center under different spinning speeds

图9为不同梁轴模型的前两阶临界转速随推力增加而变化的曲线，其变化规律与推力作用下的进动频率变化规律相似，发生了频率合并的现象。可以发现，随着推力的增加，不同模型的一阶无量纲临界转速的差异也逐渐增大。图10 为不同梁轴模型的临界推力随转速增加而变化的曲线。可见，均匀梁轴模型的陀螺效应很小，对临界推力的影响可以忽略;而对于非均匀梁轴模型，轴向力的分布发生改变，同时陀螺效应随转速的增加而增大，当转速达到某一值时，使得系统的刚性模态频率与弹性模态频率产生合并，从而使系统的临界推力突然减小。此情况对应于图10 中的阶跃部分，同时与表3数据对应，图8中的振动情况也能得以解释。所以，结构模型的非均匀性对系统的临界转速以及临界推力的影响都非常大。

图9 临界转速变化曲线Fig.9 Variation curves of critical spin speed

图10 临界推力变化曲线Fig.10 Variation curves of critical thrust

4 结论

以柔性自旋飞行器为研究对象，考虑了剪切变形对轴向位移的影响，采用有限元方法对系统进行了离散，推导出含有陀螺力矩及随动推力影响的系统运动方程，通过算例仿真对转速和随动力推力作用下的系统横向振动响应和结构失稳情况进行了分析，得到以下结论:

1)随动推力的增加会减小系统刚度，使振动幅值增大，而且会减小自旋飞行器的临界转速;当激振频率等于系统临界转速频率时，系统产生共振。

2)推力达到或超过系统临界推力时，系统发生失稳;转速的增加会降低系统的临界推力。

3)模型的非均匀性使结构的惯性、刚度和轴向力分布等发生变化，从而对系统的临界转速和临界推力造成很大影响。

综上，弹体自身旋转和随动推力的共同作用使系统的振动特性发生改变，在飞行器设计时需要引起关注。

References)

［1］Chae S，Hodges D H. Dynamics and aeroelastic analysis of missiles［C］∥Proceedings of the 44th AIAA/ASME/ASCE/AHS Structures，Structural Dynamics，and Materials Conference. Norfolk，VA:SIAM，2003:1 -6.

［2］Trikha M，Mahapatra D R，Gopalakrishnan S，et al. Structural stability of slender aerospace vehicles:part Ⅱ:numerical simulations［J］. International Journal of Mechanical Sciences，2010，52(9):1145 -1157.

［3］王良明. 大长径比弹箭在飞行时的柔性变形特性分析［J］. 兵工学报，2000，21(2):108 -111.WANG Liang-ming. An analysis on the flexibility in flight of projectiles or rockets having high L/D ratios［J］. Acta Armamentarii，2000，21(2):108 -111.(in Chinese)

［4］王良明，王中原，易文俊. 大长径比弹箭飞行中的共振条件研究［J］. 弹道学报，2001，13(1):51 -54.WANG Liang-ming，WANG Zhong-yuan，YI Wen-jun. Resonance unstability in ballistics of flexible body［J］. Journal of Ballistics，2001，13(1):51 -54.(in Chinese)

［5］许赟，谢长川，杨超. 推力作用下细长弹箭横向振动及稳定性分析［J］. 工程力学，2009，26(12):211 -215.XU Yun，XIE Chang-chuan，YANG Chao. Transverse vibration and dynamic stability analysis of slender projects under thrust［J］.Engineering Mechanics，2009，26(12):211 -215.(in Chinese)

［6］张雷，王永. 尾部有推力自由梁的振动分析［J］. 弹道学报，2010，22(1):83 -86.ZHANG Lei，WANG Yong. Vibration analysis of free-free beam with end rocket thrust［J］. Journal of Ballistics，2010，22(1):83-86.(in Chinese)

［7］何斌，芮筱亭，陆毓琪. 柔性弹箭飞行力学建模研究［J］. 弹道学报，2006，18(1):22 -24.HE Bin，RUI Xiao-ting，LU Yu-qi. A study on flight dynamic modeling of flexible shell/rocket［J］. Journal of Ballistics，2006，18(1):22 -24.(in Chinese)

［8］Zhu H L，Yu L，Liang S H，et al. Dynamic simulation of a flexible spinning vehicle with the periodic varing thrust［J］. Journal of Shanghai University:English Edition，2008，12(2):115 -119.

［9］Choi S H，Pierre C，Ulsoy A G. Consistent modeling of rotating timoshenko shafts subject to axial loads［J］. Journal of Vibration and Acoustics-Transactions of the Asme，1992，114(2):249 -259.

［10］荣吉利，徐天富，李健. 基于Timoshenko 梁模型的旋转弹箭横向振动模态分析［J］. 北京理工大学学报，2012，32(6):551 -555.RONG Ji-li，XU Tian-fu，LI Jian. Modal analysis of transverse vibration of a spinning rocket based on Timoshenko beam［J］.Transactions of Beijing Institute of Technology，2012，32(6):551 -555.(in Chinese)

［11］荣吉利，李瑞英. 大长径比自旋弹箭横向自振特性的有限元计算方法与结果分析［J］. 兵工学报，2002，23(1):79 -82.RONG Ji-li，LI Rui-ying. Finite element computational method and resultant analysis of the transverse self-oscillation characteristics of a slender spinning rocket［J］. Acta Armamentarii，2002，23(1):79 -82.(in Chinese)

［12］荣吉利，徐天富，王玺，等. 随动推力作用下柔性旋转飞行器动力学稳定性分析［J］. 宇航学报，2015，36(1):18 -24.RONG Ji-li，XU Tian-fu，WANG Xi，et al. Dynamic stability analysis of slender spinning flight vehicles under follower thrust［J］. Journal of Astronautics，2015，36(1):18 -24. (in Chinese)