滑动窗口中数据流最大频繁项集挖掘算法研究

尹绍宏，单坤玉，范桂丹

天津工业大学 计算机科学与软件学院，天津 300387

1 引言

数据流是一组大量的、连续到达的、随时间不断变化的数据序列，比如，金融领域中的股票数据，超市里的售货记录，电信行业的通话记录等等。数据流挖掘就是在这样的一些数据中挖掘出人们事先不知道但又潜在有用的知识和信息的过程。因为数据流是连续到达的而且是大量的数据，这些大量的数据是无法全部保存在内存空间中，只能读取一次或是有限的几次，而且对数据流的查询必须是实时处理的，所以对数据流挖掘算法的要求是只能扫描一次或几次，并且产生的结果通常是近似结果。显然，许多静态的数据挖掘算法并不适合于数据流挖掘。

在现实的实际应用中，人们感兴趣的都是近期的数据，所以数据流挖掘一般都是基于某个时间区间来对数据进行挖掘的，从而出现了窗口模型，常见的窗口模型[1]：界标窗口模型、滑动窗口模型和衰减窗口模型。基于界标窗口模型的代表性算法Lossy Counting[2]；基于衰减窗口模型的代表性算法FP-Streaming[3]；基于滑动窗口模型的代表性算法MineSW[4]。但是基于界标窗口模型和衰减窗口模型的挖掘都没有考虑到数据流出当前窗口的情况，挖掘的结果还是会受过时事务不同程度的影响，在实际应用中，人们关注最多的还是滑动窗口内的数据，因此本文采用的是关注和应用最多的滑动窗口模型。

频繁项集的挖掘是数据挖掘中关联规则的基本，按照频繁项集挖掘的结果，可以将频繁项集挖掘算法分为[1]完全频繁项集挖掘，频繁闭项集挖掘和最大频繁项集挖掘。因为最大频繁项集的项集数目相对很少并且已隐含所有的频繁项集，所以数据流中最大频繁项集的挖掘具有很好的时空效率并且有很大的意义，也受到了业界更多的关注。针对数据流最大频繁项集的挖掘，业内人士提出了很多经典的算法，主要包括estDec+[5]、INSTANT[6]和DSM-MFI[7]等算法，上述算法能一次性扫描流过的数据，但仍然存在不足，而且以上算法都是基于界标窗口的，包含大量的历史数据，但是人们更关心的是近期的数据，即滑动窗口中的数据，如算法FPMFI-DS+[8]等。

算法MFISW[9]提出了基于向量的数据流滑动窗口中最大频繁项集挖掘方法，通过超集检测挖掘最大频繁项集，虽然具有较好的时空效率，但只引用单个频繁二项集矩阵进行相关操作；算法NSW[10]采用二进制矩阵表示滑动窗口中的事务列表，进行频繁项集的挖掘；算法MMI-BET[11]提出数据流中基于滑动窗口的最大频繁项集挖掘算法，采用超集检测和索引链表的方法检测和存储最大频繁项集，但搜索时间效率较低；算法AFMI[12]提出基于事务矩阵挖掘最大频繁项集，但挖掘过程需迭代多个精简矩阵并进行逻辑操作，时间效率较差，同时基于算法AFMI提出滑动窗口数据流最大频繁项集算法AFMI+[12]，基于以上相关算法的研究和启发，本文提出了滑动窗口中数据流最大频繁项集挖掘算法SWM-MFI，同时引入两个矩阵：事务矩阵和二项集矩阵，两个矩阵均采用二进制0-1表示并通过两个矩阵的相关操作和子集检测快速挖掘出最大频繁项集存储到数组MFI中。

2 基本概念

设项I={I1,I2,…,Im}，数据流DS是一组连续不断到达的并且大小可能无限的数据项序列{T1,T2,…,Ti,…,Tn,…}，其中Ti表示第i个到达的事务，而且对于任意Ti，都有Ti⊆I。

定义1项的集合被称为项集，k-项集[13]是指包含k个项的集合。

定义2对于∀X⊆I，把窗口中包含X的事务数目称为X的支持度，记为sup(X)。

定义3滑动窗口W没有明确的起始点，终止点为窗口的当前时刻，窗口的大小即|W|=窗口中包含事物的数目，该值由用户预先自行设定。每当一个新事物到达时，旧的事务就被删除并被新事务直接覆盖，窗口就滑动一次，事务矩阵不断被更新。

定义4给定W和最小支持度min_sup，对于∀X⊆I，若有sup(X)≥min_sup，则称X为滑动窗口W中的频繁项集。

定义5（最大频繁项集）给定滑动窗口W和最小支持度min_sup，∀X⊆I，若sup(X)≥min_sup并且∀(X⊂Y∩Y⊆I)，其中Y为项集X的超集，均有sup(Y)＜min_sup，则称X为滑动窗口W中的最大频繁项集。

定义6[5]全序关系≺。根据字典中的字母顺序，若X小于Y，则记为X≺Y，例如A≺B≺C。同理，定义两个项集的字典顺序为≺，例如A≺ABC≺CD。

假定文中所有的项都是按照全序关系排列的。

3 SWM-MFI算法

3.1 算法使用的数据结构

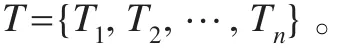
（2）二项集矩阵B：假设项集中有m个项，则构造一个(m-1)×(m-1)的二项集矩阵，首先将矩阵中的每一个元素初始化为0。对于频繁1-项集L1中的两个项Ii，Ij，若Ii≺Ij，则取事务矩阵A中的第i行和第j行进行逻辑与操作，若其支持度大于或等于min_sup，则项集{Ii,Ij}为频繁2-项集，并将Bi,j置为1，否则置为0。

3.2 SWM-MFI算法的基本思想

频繁(k-1)-项集的扩展：频繁(k-1)-项集可以扩展为k-项集，扩展条件如下：设{Ii1,Ii2,…,Ii(k-1)}是频繁(k-1)-项集，在二项集矩阵B中，若B[i(k-1),iu]=1，其中Ii(k-1)≺Iiu，并且B[i1,iu]=B[i2,iu]=…=B[i(k-2),iu]=1，那么{Ii1,Ii2,…,Ii(k-1),Iiu}可被扩展为k-项集，然后对事务矩阵A中这k个项对应的行做逻辑与操作，若所得的值大于或是等于min_sup，则{Ii1,Ii2,…,Ii(k-1),Iiu}就是频繁k-项集。然后对{Ii1,Ii2,…,Ii(k-1),Iiu}中的最后一项Iiu进行扩展，即重复以上步骤，直至不能再扩展为止。

最大频繁项集的产生：子集检测，首先将频繁1-项集的集合L1存储到最大频繁项集MFI中，然后依次检查MFI中是否存在频繁2-项集{Ii1,Ii2}的子集，若有，则删除该子集，然后将该频繁2-项集添加到最大频繁项集MFI中；若没有，则直接添加到MFI中，重复以上步骤，直至将扩展到最后的一个频繁项集检测完MFI是否有其子集为止，算法结束，MFI中存放的就是窗口中所有的最大频繁项集。

例子：以表1所示的事务数据流为例，介绍SWM-MFI算法的基本原理，设min_sup=2，|W|=5。

表1 事务数据流

（1）窗口初始阶段

当窗口内的事务数据小于窗口的大小|W|时处于窗口初始阶段。在此阶段，新的数据事务不断进入窗口，直到窗口满为止。

则表1的事务数据流的事务矩阵A如表2所示。

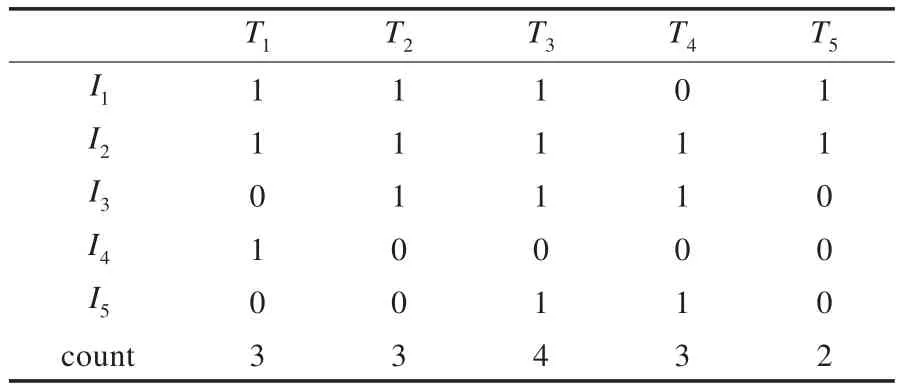
表2 窗口初始阶段构造事务矩阵A

（2）窗口滑动阶段

当窗口已满时处于滑动窗口阶段。算法NewMoment[14]采用左移操作删除旧事务，再将新事务添加到最右边的位置，极大地降低了时间效率。本文采用的方式是将最旧的事务T1被新到来的事务T6直接覆盖，提高了时间效率。则表2中的事务矩阵A更新为如表3。

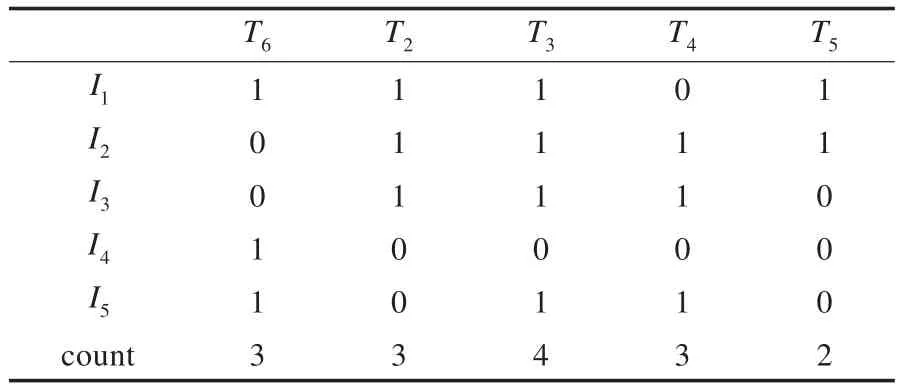
表3 窗口滑动阶段更新的事务矩阵A

（3）最大频繁项集产生阶段

步骤1计算表3中的事务矩阵A每行中1的个数，若大于等于min_sup，则为频繁1-项集。得到L1={I1,I2,I3,I5}，并将频繁1-项集添加到最大频繁项集MFI中，得到MFI={I1,I2,I3,I5}。

步骤2构造二项集矩阵B。表4所示，得到L2={{I1,I2},{I1,I3},{I1,I5},{I2,I3},{I2,I5},{I3,I5}}。

步骤3取出L2中的第一个频繁2-项集{I1,I2}，检测MFI中是否有该项集的子集，有其子集I1和I2，将子集删除，并将该2-项集添加到MFI中，重复以上步骤，得到MFI={{I1,I2},{I1,I3},{I1,I5},{I2,I3},{I2,I5},{I3,I5}}。

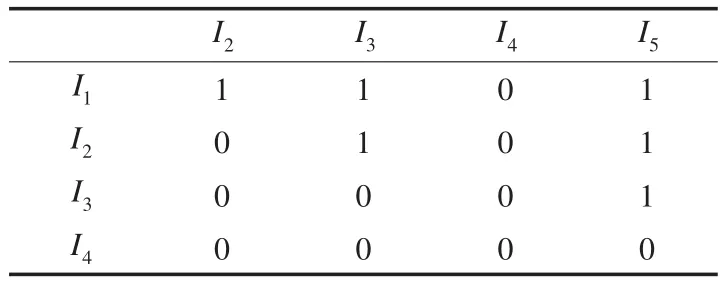
表4 二项集矩阵B

步骤4根据L2中的项和B中的信息，可以将频繁2-项集扩展到3-项集{{I1,I2,I3},{I1,I2,I5},{I1,I3,I5},{I2,I3,I5}}，再将事务矩阵A中的各相关行做逻辑与运算，求其支持度，得到L3={{I1,I2,I3},{I2,I3,I5}}。然后取出第一个频繁3-项集{I1,I2,I3}，检测MFI中是否有其子集，将其子集删除，并将该项集添加到MFI中，重复以上步骤得到MFI={{I1,I5},{I1,I2,I3},{I2,I3,I5}}。本例不能再产生频繁4-项集，算法结束。

最后得到的滑动窗口中的所有最大频繁项集为MFI={{I1,I5},{I1,I2,I3},{I2,I3,I5}}。

3.3 SWM-MFI算法的流程

根据上述例子的分析，该算法大致分为三个关键步骤：窗口初始阶段、窗口滑动阶段，最大频繁项集产生阶段。

算法的伪代码如下：

算法1伪代码如下：

输入：数据流DS，滑动窗口的大小w=|W|

输出：事务矩阵A。最大频繁项集MFI

（1）滑动窗口中的事务Tj

（2）Else//窗口已满，进入窗口滑动阶段

算法2伪代码如下：

算法3伪代码如下：

4 实验结果分析

算法采用的实验环境：Windows XP操作系统，内存2 GB，2.67 GHz CPU的平台；编程语言C#，开发软件是Microsoft Visual Studio 2010。采用的实验数据是由IBM data generator（http：//www.almaden.ibm.com）生成的模拟数据。采用的数据集是稀疏集T10I4D100K和稠密集T40I10D100K，其中T表示事务的平均长度，I表示最大频繁项集的平均长度，D表示数据流中事务的总数，即实验中的事务总数是10万条，最大频繁项集的平均长度为4和10。设定滑动窗口大小为|W|=1 000。

如图1所示，比较了算法在两个数据集上的性能。从图中可以看出，随着处理事务数目的不断增多，两个数据集的运行时间均呈近似线性增长的趋势，而且两个数据集的增长趋势近似相同，但在稠密数据集上的运行时间要远远高于稀疏数据集的运行时间，这是因为稠密数据集事务和最大频繁项集的平均长度都比较长，在滑动窗口，更新以及寻找子集求得最大频繁项集的过程中耗费的时间较长。

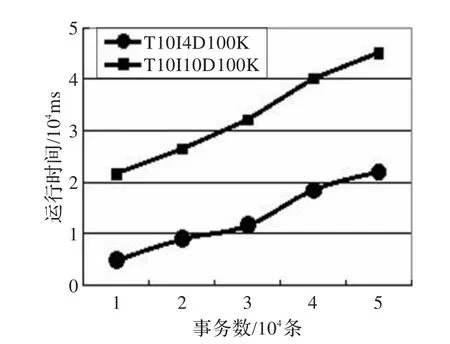
图1 不同数据集上算法的运行时间

图2通过设定不同的最小支持度min_sup来测试min_sup对算法性能的影响。在稀疏集T10I4D100K中分别测试了四个不同的min_sup，从图中可以看出，随着事务数的不断增加，每个min_sup耗费的时间呈平稳增长的趋势。在处理相同事务数的情况下，min_sup越小，算法运行的时间越长，这是因为min_sup越小，所得到的频繁项集越多，在插入以及寻找子集的过程中需要耗费较长的时间。

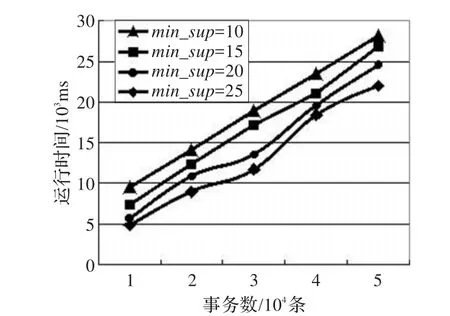
图2 不同最小支持度下算法的运行时间

图3通过设定不同的滑动窗口大小|W|，来测试|W|对算法性能的影响。在两个数据集中分别测试了5个不同的|W|，其中min_sup=80，挖掘10 000条事务。从图中可以看出稀疏数据集中的事务数据随着|W|的增大，运行时间也在增加，但是增速很缓慢；稠密数据集增速相对较快。随着|W|的增大，事务矩阵和二项集矩阵的规模会逐渐扩大，窗口的滑动时间增加，从而造成算法的运行时间增加，但增速还是比较缓和。

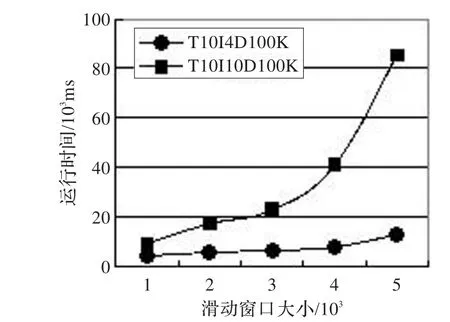
图3 不同|W|算法的运行时间

如图4和图5所示，实验对SWM-MFI和AFMI以及AFMI+算法进行了比较。AFMI是基于事务矩阵初步挖掘最大频繁项集，然后通过事务矩阵的相关操作产生压缩矩阵和交集矩阵，再从交集矩阵中进一步挖掘最大频繁项集，显然此算法在运行过程中需要不断迭代事务矩阵，并在多个矩阵上进行逻辑运算，对事务矩阵进行排序和多次扫描来搜索最大频繁项集，并需要不断剪枝，因此耗费了大量的时间。而SWM-MFI算法在挖掘最大频繁项集的过程中，省去了剪枝操作，只基于两个矩阵进行挖掘，无需迭代和排序，只需一次扫描事务数据，提高了挖掘的时间效率。图4是在挖掘1 000条事务，窗口大小|W|=1 000的前提下，即滑动窗口处于初始阶段，没有数据需要移出，在稀疏集T10I4D100K上进行的实验，相当于是在静态数据集上挖掘最大频繁项集。在不同最小支持度下算法SWM-MFI和AFMI的运行时间比较，如图4所示。通过实验可以看出，随着最小支持度的不断减小，本文算法的时间效率提高的越明显。

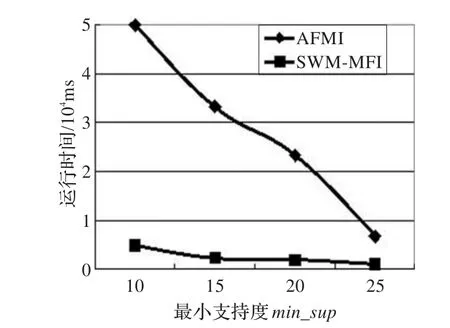
图4 不同最小支持度下，不同算法运行时间的比较

图5是将算法SWM-MFI和AFMI+进行比较，AFMI+算法是基于算法AFMI研究的挖掘滑动窗口中数据流最大频繁项集，存在的不足与算法AFMI相同。本实验的前提是在稀疏集T10I4D100K中，滑动窗口大小|W|=1 000，最小支持度min_sup=9。从图中可以看出，在处理不同数目的事务下，本算法的时间效率要远远高于算法AFMI+的时间效率。

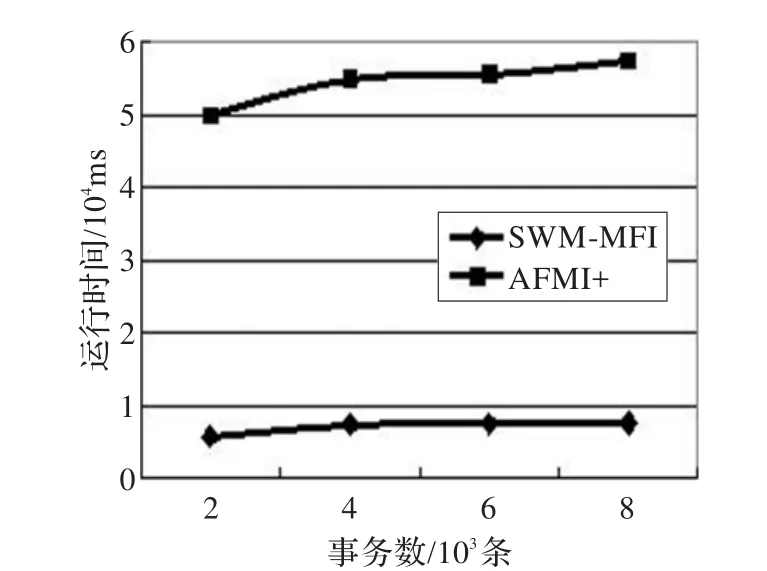
图5 不同事务数下，不同算法的运行时间的比较

5 结束语

本文提出的在滑动窗口中基于矩阵的数据流最大频繁项集挖方法SWM-MFI，引入了两个矩阵：事务矩阵和二项集矩阵，通过两个矩阵的相关操作并采用寻找子集的方法挖掘出最大频繁项集存储到数组MFI中。通过与算法AFMI，AFMI+的比较，证明了该算法具有很好的时效性。

[1]毛伊敏.数据流频繁模式挖掘关键算法及其应用研究[D].长沙：中南大学，2011.

[2]Manku G S，Motwani R.Approximate frequency counts over data streams[C]//Proceeding of the 28th International Conference on VLDB，Hong Kong，2002.

[3]Giannella C，Han J，Pei J.Mining frequent patterns in data streams at multiple time granularities[C]//Proceeding of the NSF Workshop on Next Generation Data Mining，2002：191-212.

[4]Cheng J，Ke Y，Ng W.Maintaining frequent itemsets over high-speed data streams[C]//Proceeding of the 10th PAKDD，2006.

[5]Lee Daesu，Lee Wonsuk.Finding maximal frequent itemsets over online data streams adaptively[C]//Proc of Fifth IEEE InternationalConference on Data Mining.Washington DC：IEEE Computer Society，2005：266-273.

[6]Mao Guojun，Wu Xindong，Zhu Xingquan.Mining maximal frequent itemsets from data streams[J].Joumal of Information Science，2007，33（3）：251-262.

[7]Li Hua-Fu，Lee Suh-Yin，Shan Man-Kwan.Online mining（recently）maximal frequent itemset over data streams[C]//Proc of the 15th International Workshops on Research Issuesin DataEngineering：Stream DataMining and Application，2005：11-18.

[8]獒富江，颜跃进.在线挖掘数据流滑动窗口中最大频繁项集[J].系统仿真学报，2009，21（4）：1134-1139.

[9]徐嘉莉，陈佳，胡庆，等.基于向量的数据流滑动窗口中最大频繁项集挖掘[J].计算机应用研究，2012，29（3）：837-840.

[10]张月琴.滑动窗口中数据流频繁项集挖掘方法[J].计算机工程与应用，2010，46（16）：132-134.

[11]杨路明，刘立新，毛伊敏.数据流中基于滑动窗口的最大频繁项集挖掘算法[J].计算机应用研究，2010，27（2）：519-522.

[12]张月琴，陈东.数据流最大频繁项挖掘方法[J].计算机工程，2010，36（22）：86-90.

[13]韩家炜.数据挖掘概念与技术[M].北京：机械工业出版社，2012.

[14]Li Hua-Fu，Ho Chin-Chuan，Kuo Fang-Fei.A new algorithm for maintaining closed frequent itemsets in data streams by incremental updates[J].Expert Systems with Applications，2009，36（2）：2451-2458.