利用CUDA提高内存数据聚类效能的研究
董丽丽,董 玮,张 翔
西安建筑科技大学,西安 710055
1 引言
聚类分析通常用于将数据划分成有用的或有意义的组或簇,在心理学、生物学、统计学、信息检索、机器学习和数据挖掘中扮演着重要的作用。在心理学领域,特定的人群存在着相应的心理学特征,将此类人群提取特征值并进行聚类,可以帮助心理学专家对此类人群的心理特征进行分析。K-Means算法作为传统的数据挖掘方法,在心理学数据的聚类分析中具有重要作用。但K-Means算法存在初始聚类中心敏感问题,导致聚类有效性降低。针对K-Means算法的中心敏感问题,Bradley P S等学者提出[1],在聚类分析的数据中随机选取多个子样本,对选取的子样本重复执行K-Means算法得到优化的聚类中心,再对整个数据集进行K-Means算法聚类。然而,此方法受到子样本集选取方式的影响,只是一种次优结果。将智能算法与传统数据挖掘方法相结合的方式在近些年来广泛被研究[2-6],可有效提高聚类有效性,但在实际应用当中,执行效率较低。针对传统数据挖掘算法的效率问题,将Mapreduce编程模型运用到提高大规模数据聚类效率方面已经成为热点,薛胜军等学者利用开源组织apache基金会下的hadoop项目[7],实现了K-Means算法的并行化,提高了效率。但在实际运用当中,心理学数据不具备网络数据的即时性、高访问性、交互性和大规模性,利用云平台进行此类数据挖掘并不适合,并且由于网络的延迟性和不可靠性,心理学等内存数据在利用hadoop平台实际挖掘当中,并不比传统方法在执行效率上好多少。
CUDA技术是NVIDIA公司针对其GPU(Graphic Processing Unit)产品所发明的一项高性能计算技术,此技术非常适合心理学等数据规模较小的内存数据挖掘,此项技术为在有限时间内多次聚类,并从多次聚类结果中观察最优结果提供了可能。Kumar等学者[8]利用CUDA实现了高斯混合模型期望最大化算法的并行化,加速比为165倍;张繁等学者[9]将CUDA应用于计算蛋白质分子长,对比CPU加速比为7.5倍;Takahashi等学者[10]利用CUDA加速了三维亥姆霍兹方程,加速比为23倍;Labaki等学者[11]把CUDA应用到二维势问题和二维弹性静力学问题,加速比分别为56.8和39.6倍。
为了解决上述问题,本文提出了一种基于CUDA技术和FP-Tree关联迭代相结合的K-Means聚类算法—AIK-Means(Associated IterationK-means)算法,利用CUDA解决多次聚类的执行效率问题。利用Chameleon层次聚类算法找出K-Means算法的初始中心。Chameleon算法是一种基于层次的聚类图算法,该算法利用基于图的方式得到初始数据的划分,使用簇间的接近性和互连性概念和簇的局部建模,发现具有高质量的不同形状、大小和密度的簇[12]。所以本文首先对内存数据进行初步聚类,得到K-Means算法的初始参数,从而利用Chameleon算法聚类缓解K-means初始聚类中心的随机性和先验性导致聚类结果不稳定的问题。利用FP-Tree对多次聚类结果进行关联分析,从K-Means算法的执行结果入手,降低K-Means算法的中心敏感问题,提高聚类有效性。
2AIK-Means算法
2.1 AIK-Means算法框架
AIK-Means算法主要流程如图1所示。
数据流在显卡设备(GPU)中利用CUDA技术加速计算,在主机设备(CPU)中利用.NET Framework平台进行IO读写和任务处理。AIK-Means算法思想如下。第一步:将心理学数据预处理,以达到层次聚类算法Chameleon所要求的格式。第二步:利用Chameleon算法进行初始聚类,为下一步K-Means算法找出K个初始簇。第三步:将初始簇利用K-Means算法进一步深层聚类,找出K个初始簇的收敛中心点。第四步:重复第二步、第三步n次,得到n个聚类结果。第五步:利用FP-Tree对n次聚类结果进行关联分析,在多次聚类结果中找出最终的稳定结果。
2.2 心理学数据的预处理
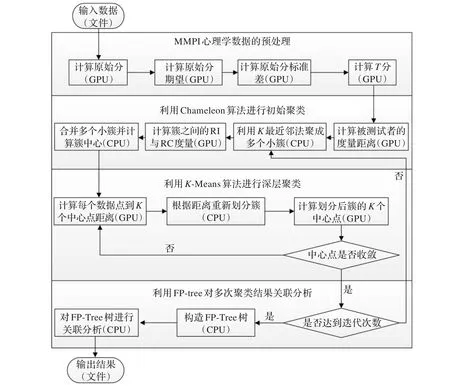
图1 算法流程图
本文利用行为心理学中的MMPI(Minnesota Multiphasic Personality Inventory)量表集,采集某集团单位人群的行为心理学数据,对人群进行聚类,帮助心理学研究者分析人群的多项人格。MMPI是行为心理学最为复杂和繁琐的一种测试,但其准确度与其他量表相比较为准确[13]。MMPI的第一步为获得测试数据,计算每个测试对象的25个测试项目的原始分,分为两种量表,共566道测试题。由于每项测试量表题目数量不同,导致原始分总分分值不同,无法直接比较,需要将各个量表的原始分数进行归一化操作。第二步就需要通过公式(1):

计算出各个量表归一化为标准分T,其中T为向量,向量中每一分量代表各个量表的标准分。X为各个测试量表的原始分组成的原始分向量,M与SD分别为各个测试量表正常组原始分数的期望及标准差所组成的向量。MMPI数据预处理的重点在于将原始分转换为标准T分,求其期望M和标准差SD。
在主机设备中计算期望M和标准差SD需要多次迭代,此时迭代规模随着数据规模的增长而增加。可利用CUDA技术在同样的数据规模中将迭代执行转换为并行执行,从而减少迭代规模,提高执行效率。在CUDA并行环境中,可利用缩减树算法求出期望M和标准差SD,如图2所示。
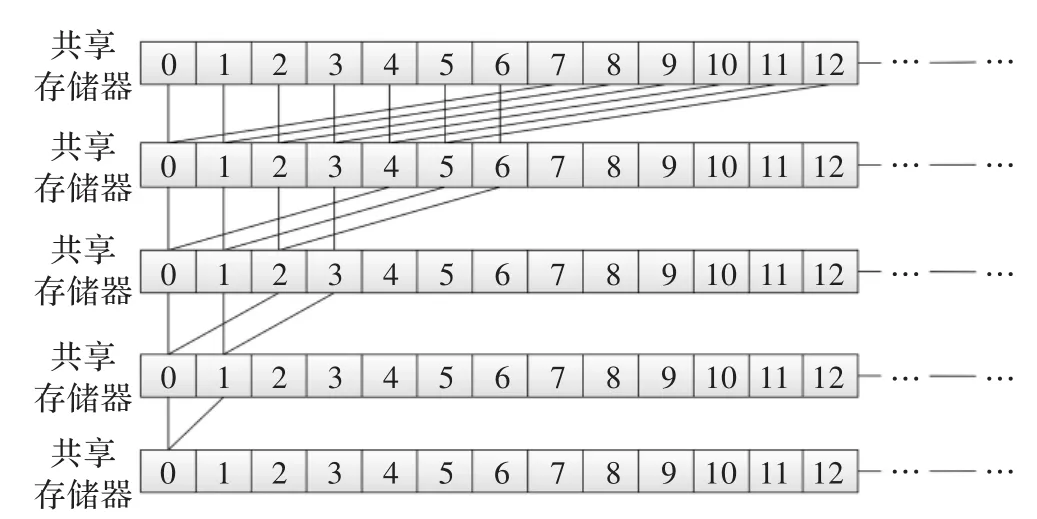
图2 缩减树算法
图2中为前13个被测试者的某一项测试量表原始分通过缩减树算法并行相加,通过5次迭代,将相加结果存入共享数组首元素中,此结果除以数组长度,即为此项测试量表的期望M。具体步骤如算法1所示。
算法1缩减树算法
函数说明:函数Expectation为在GPU上运行的核函数,本文算法函数前若带Kernel function关键字皆为核函数。输出形参R为在CUDA上各个线程块之和的数组,将R拷贝到主机内存中,利用CPU求公式(2)


在算法1中,threadIdx、blockIdx、gridDim、blockDim和shared均为CUDA内置变量。threadIdx为线程块内线程标号;blockIdx为线程格内线程块标号;gridDim为线程格尺寸,通过此变量可计算出线程块的数量;blockDim为线程块尺寸,通过此变量可计算线程块内线程数量;shared为GPU块内共享内存数组;CUDA内置函数synchronize threads为同步函数,使所有线程在当下时刻同步。对于求SD函数Kernel function StandardDeviation(T,M,R),利用函数Expectation求得期望M,作为其第二实参传入。将函数Expectation第4 行shared[tid]←shared[tid]+T[i]改 为shared[tid]←shared[tid]+(T[i]-M)2,即为函数StandardDeviation,利用缩减树算法的结果开平方即可求得SD。
2.3 利用CUDA改进Chameleon算法
Chameleon算法是一种两阶段聚类层次算法,第一阶段采用K最邻近法把点分成多个小簇,把一个点和其最近邻的k个点连接起来;第二阶段根据相近程度合并多个小簇,计算任意两个簇的互联性RI和紧密性RC,当两个指标都较大时合并两个簇。RI的公式(3)与RC的公式(4)如下所示。
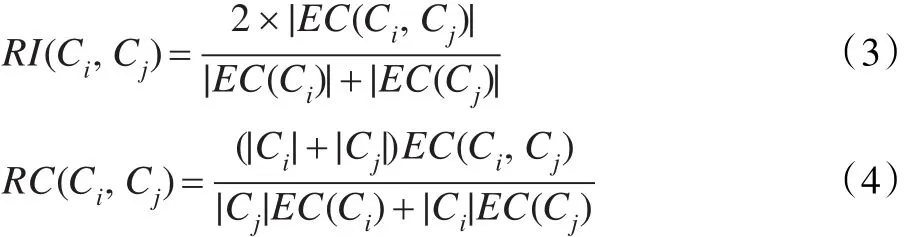
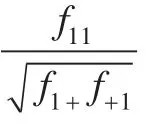

计算出在下三角阵H中的位置(i,j),其中,k为数组R下标,m为当前矩阵的行数,当k及m使不等式成立时,i=m,j=k-m(m-1)/2。利用(i,j)找出向量数组R中的向量Ri与向量Rj,求出两向量间的对称度量距离,存入数组H下标为k的元素中。在每个CUDA线程中,通过上述过程计算得到向量数组R中Ri与Rj向量的距离,存入数组元素Hk中。如图3所示。
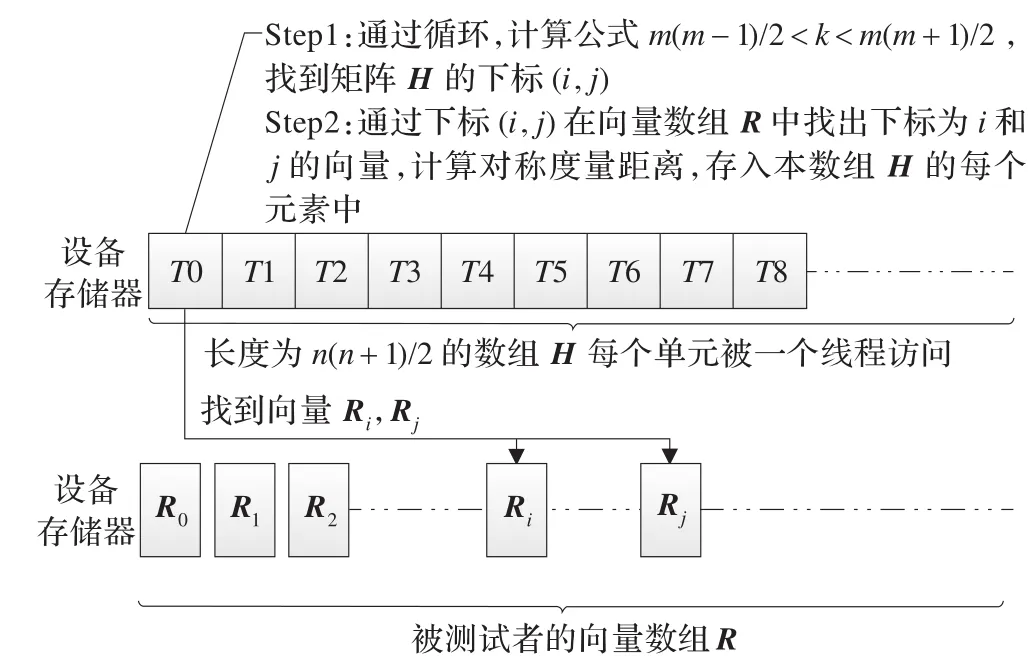
图3 计算向量间距离
将数组H拷贝回主机存储器,遍历数组H,采用K最近邻法构造多个小簇,每个簇的元素数量不大于K,并计算小簇i的信息如点的个数|Ci|,簇内所有边权重和EC(Ci),存入数组R中。具体步骤如算法2所示。
算法2计算向量间距离伪代码

Chameleon算法的第二阶段的第一步与核函数CalculateDistance执行过程相似,R由存储向量组改为存储小簇组,H数组记录小簇之间RI×RC的距离。第二步,将数组R拷贝回主机存储器,设定阈值u,遍历数组H,当元素i中的RI×RC>u时,合并i所代表的两个小簇,将新簇组存入数组R中并且拷贝到设备存储器,重复第一步、第二步过程,直到条件RI×RC>u不再满足条件为止。
2.4 利用CUDA改进K-Means算法
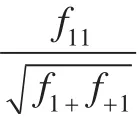
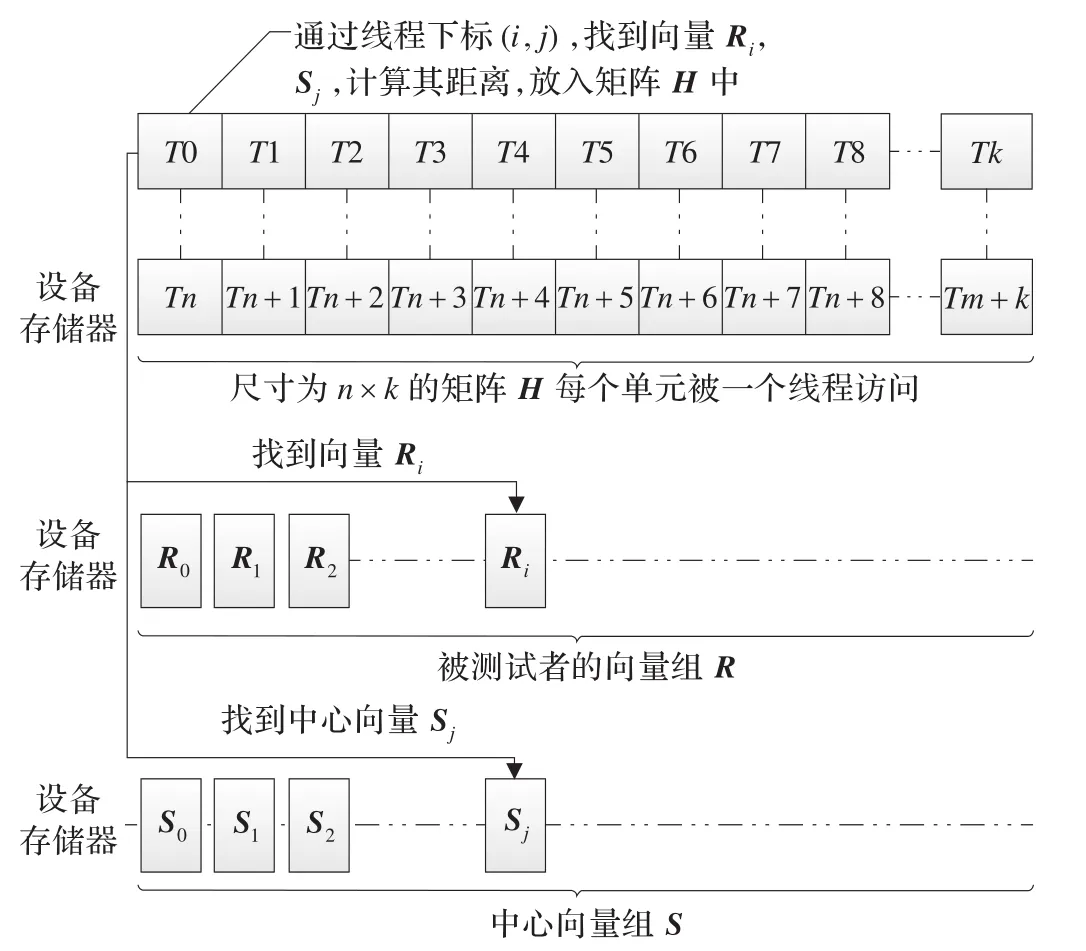
图4 计算向量组R与向量组K每对向量的距离
将矩阵H从设备存储器拷贝回主机存储器中,遍历矩阵H,分别找出与K个中心向量距离最近的向量组R1~k,组成K个簇。具体步骤如算法3所示。
算法3计算中心点与数据点距离伪代码


第二阶段,将每个簇的向量组R拷贝到设备存储器中,利用2.1节介绍的缩减树算法计算新的中心向量,作为下一次迭代第一阶段的K个簇的中心向量。重复第一阶段和第二阶段,直到中心向量收敛为止。
2.5 构造FP-Tree数据结构
将2.3节中的Chameleon算法与2.4节中的K-Means算法运行多次,组成事务型数据,数据格式与内容如图5所示。

图5 事务型数据格式(部分数据)
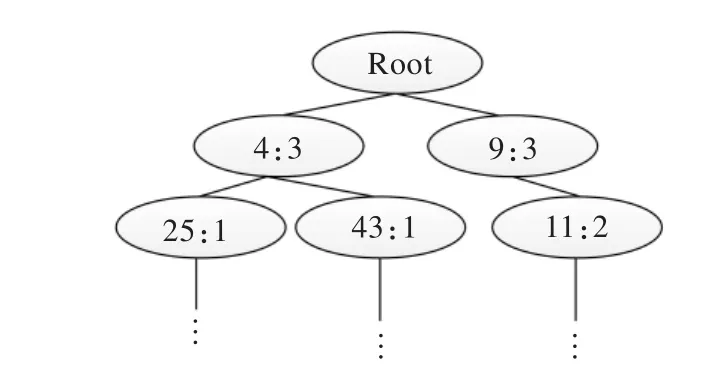
图6 FP-Tree示意图
Root为根节点,Root的每一个子树为一簇,簇中节点包含两部分信息,冒号前部为被测试者编号,冒号后部为被测试者编号在某一簇的多次结果中的某个结果中出现次数。具体步骤如算法4所示。
算法4构造FP-tree伪代码


统计Root的每个子树中每个被测试者出现的次数,当出现次数大于其在整个FP-Tree树中出现次数的1/2时,将每个子树中符合条件的被测试者编号组成频繁项集。具体步骤如算法5所示。
算法5构造频繁项集伪代码

算法6 Traversal函数伪代码
在进行造林之后需要进行及时的验收,但是在实际的验收工作中存在一定的问题。第一,对需要验收的项目没有进行及时的自查验收,没有进行建档工作。第二,一些验收工作只是在表面上进行,没有真正落实到位。第三,验收图纸和实际的情况存在一定才差距。


3 实验
3.1 实验环境
实验环境:CPU:Intel i7-3770;CPU频率:3.4 GHz;CPU核心数/线程数:4/8;主机内存:8 GB;GPU:NVIDIA GTX 660;设备内存(显卡):2 GB;CUDA版本:5.0;操作系统:Windows7。
3.2 实验数据
本文的实验数据为某集团单位员工历年来MMPI心理学测试数据,大小为353 MB,以行为单位,测试数据有907 689条,由5个.csv文件组成,数据格式如图7所示。

图7 某集团单位员工心理测试数据
逗号将每一列分开,第一列为员工测试编号,后面每一列对应于一道MMPI测试题,第一列为第一题,第二列为第二题,以此类推。答题中0代表肯定回答,1代表否定回答。
3.3 实验分析
(1)CUDA并行加速环境与纯CPU串行执行环境下AIK-Means算法的执行效率比较
为比较算法性能,本文分别对AIK-Means算法的各个部分在CUDA执行环境(以下表格中均简称并行加速环境)与纯CPU执行环境(以下表格中均简称串行环境)下进行比较,利用加速比度量算法的效率。数据预处理的实验结果如表1所示。

表1 数据预处理实验结果
由表1可知,在串行环境下CPU计算MMPI中T分的时间主要用在计算其期望及标准差,在并行加速环境下把计算T分期望及标准差交给GPU,CPU主要工作变为IO读写文件,将算法的预处理计算部分用于CUDA并行计算,对程序的加速比有很大提高。Chameleon部分的实验结果如图8、图9所示。
由图8、图9可以得出,当RI×RC阈值递增时,Chameleon算法的串行环境版本和并行加速版本都出现递减情况。经分析,Chameleon算法的串行环境版本不仅需要在算法的第一阶段遍历k最邻近图和在算法的第二阶段遍历最邻近簇,还需要计算第一阶段向量组成的下三角矩阵元素和第二阶段簇组成的下三角矩阵元素。将Chameleon算法经过CUDA并行化后,主要并行化的部分为计算其两个阶段的下三角矩阵,但遍历k最邻近图及最邻近簇依然在CPU上执行,与串行环境算法的遍历部分一致。随着RI×RC阈值增大,满足合并条件的簇越少,合并过程所付出的时间代价就越少,即串行环境版本和并行加速版本算法的遍历部分时间代价都会减少。K-Means部分的实验结果如图10、图11所示。
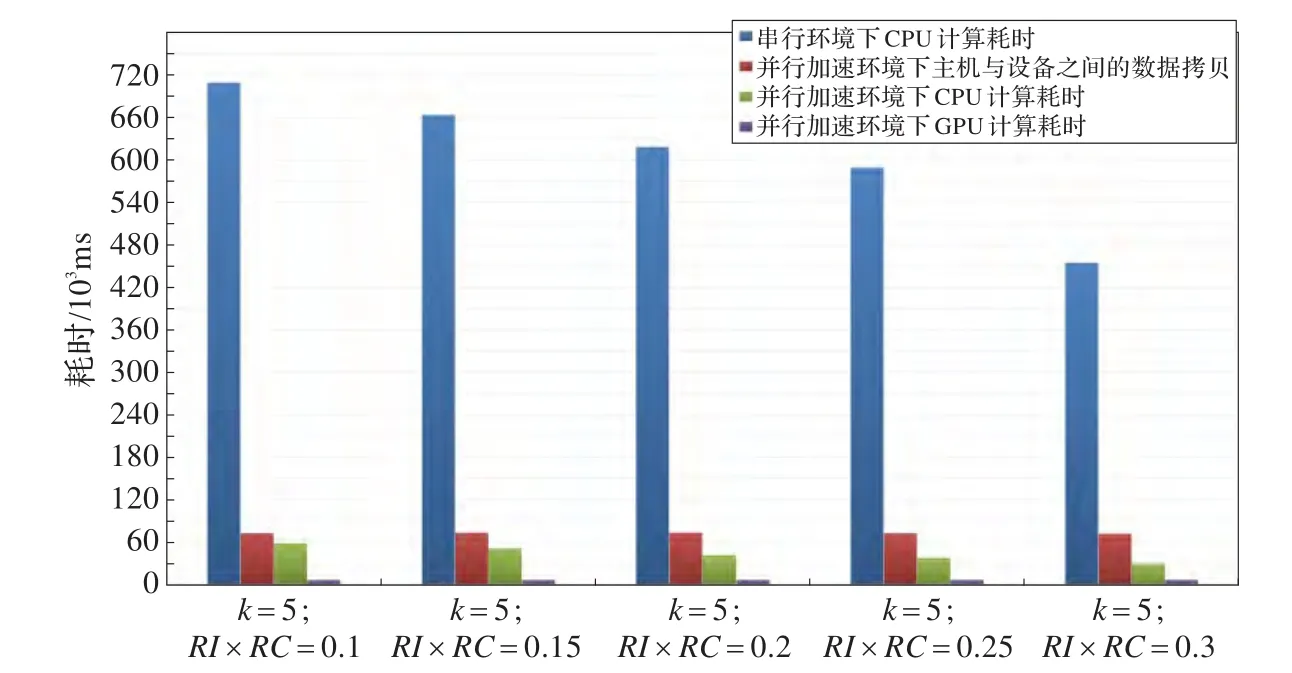
图8 Chameleon算法部分在并行与串行环境下的耗时对比
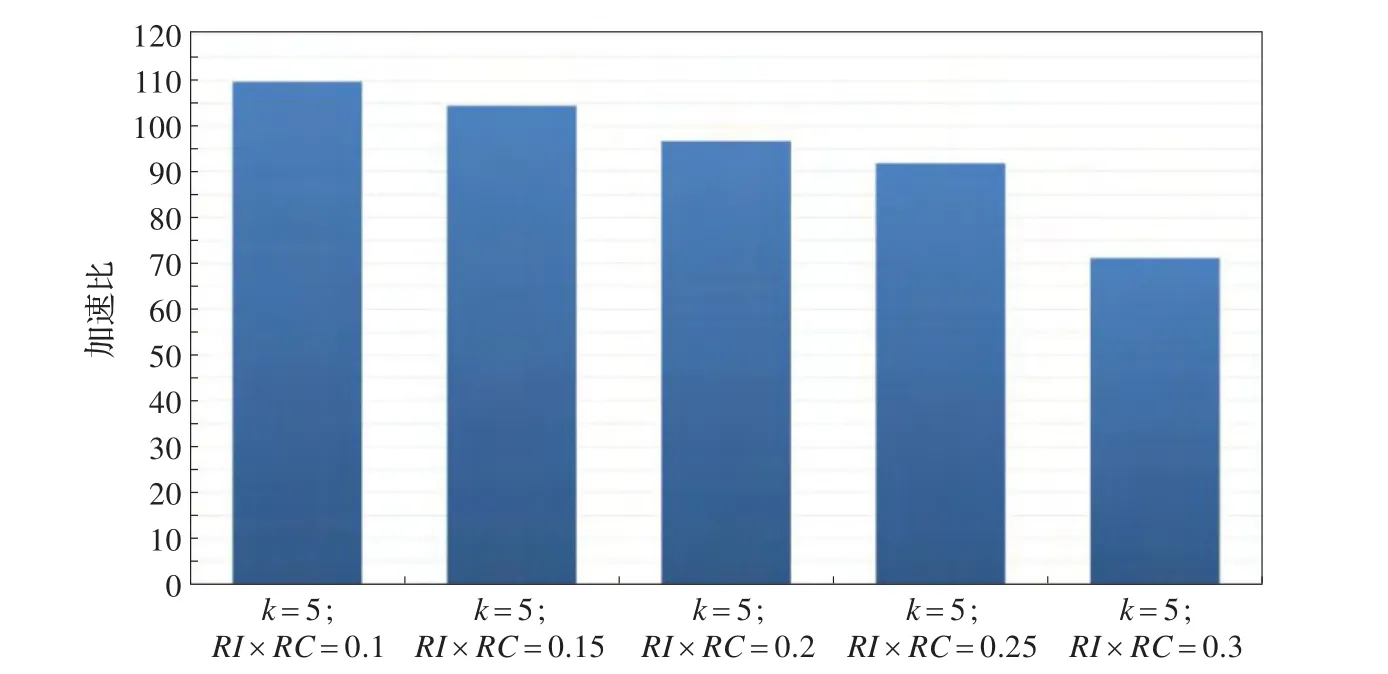
图9 Chameleon算法部分的加速比
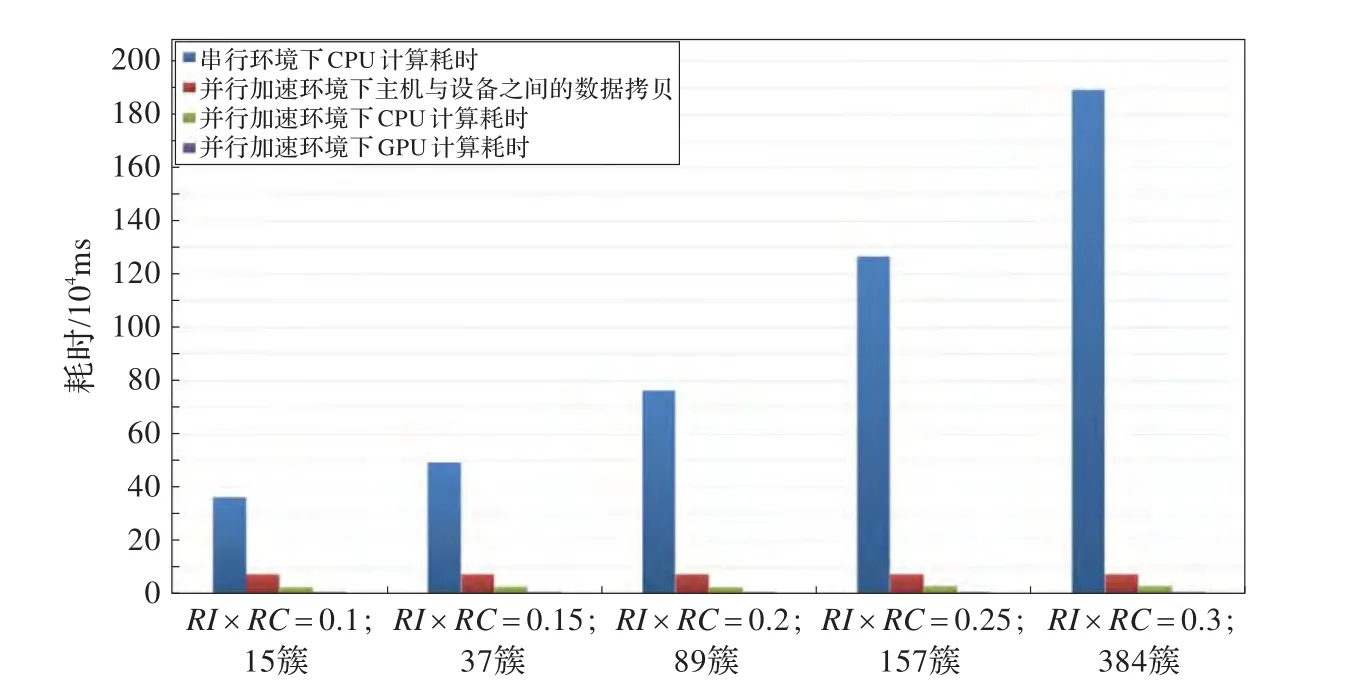
图10 K-Means算法部分在并行与串行环境下的耗时对比
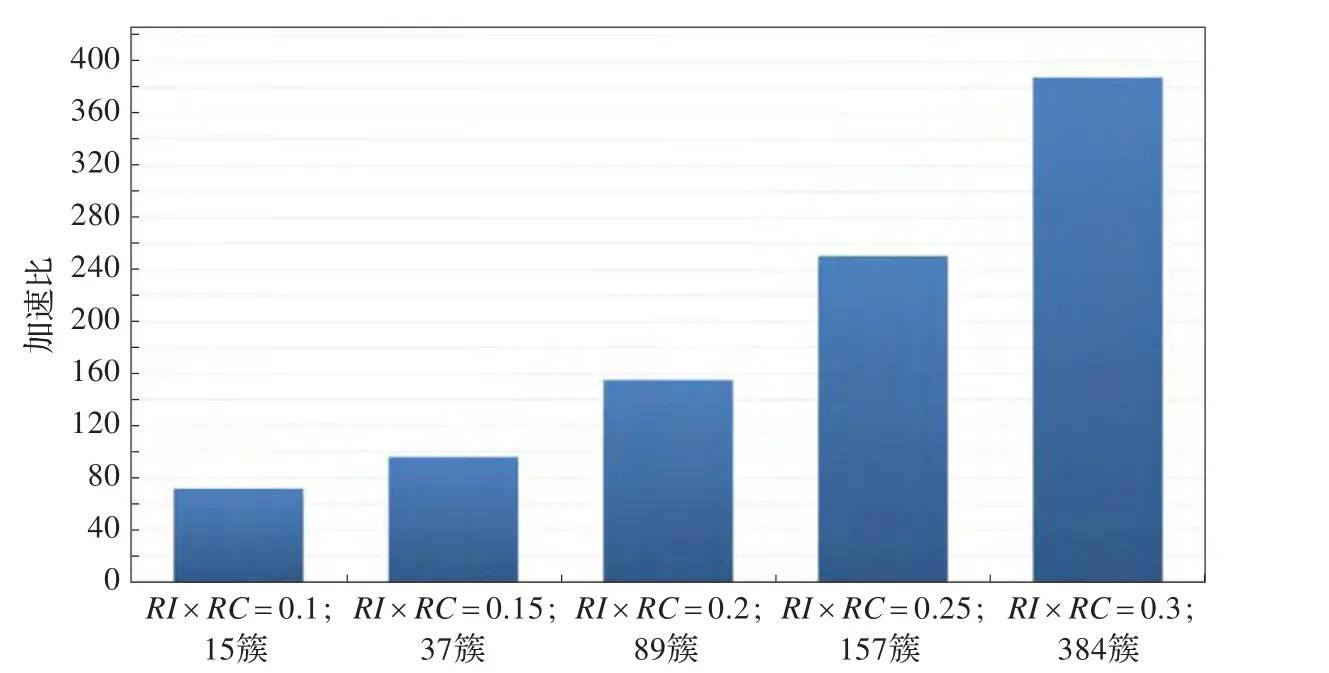
图11 K-Means算法部分的加速比
由图10、图11可以得出结论,随着初始簇的数量K越大,K-Means算法部分的加速比越高。经分析,K-Means算法的两个阶段计算每个点与中心点距离和求中心点都进行了CUDA并行化改进,将算法中所有的数值计算都在GPU上运行,CPU负责数据拷贝与调度,使得算法效率大大提高,尤其是在初始簇越多的情况下,加速比也随之迅速提高。AIK-Means算法的总体比较如图12、图13所示。
从图12、图13上分析,RI×RC阈值的提高,增加了K-Means的初始簇个数K,造成了算法K-Means阶段计算规模增加,加速比也随之增加,由此可得出结论,当AIK-Means算法计算规模和计算数据量增大时,算法效率更高。
(2)AIK-Means算法与K-Means算法聚类纯度的比较
实验采用UCI机器学习数据库的三个权威数据集进行实验,分别为Iris、Wine和Glass。如表2所示。
本文采用纯度标准作为聚类结果的有效性评估方法。设类簇Ci的大小为ni,则该类簇的纯度定义为公式(6):
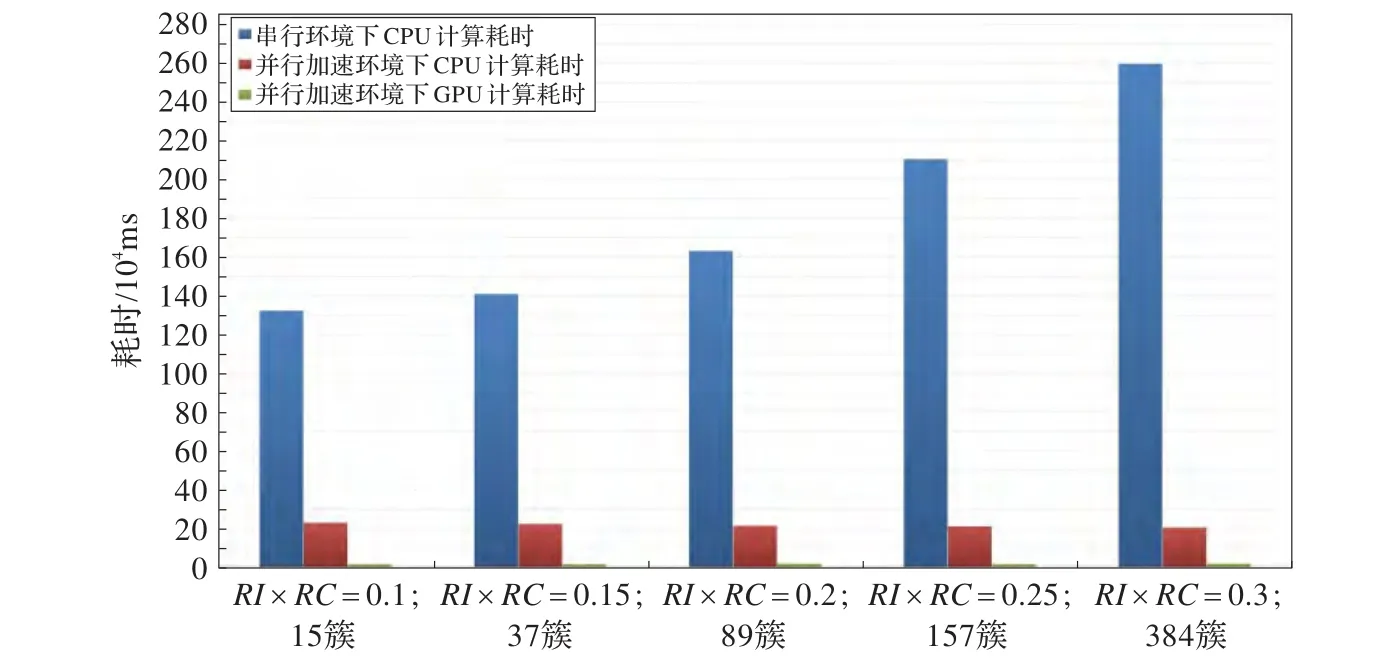
图12 AIK-Means算法总体在并行与串行环境下的耗时对比
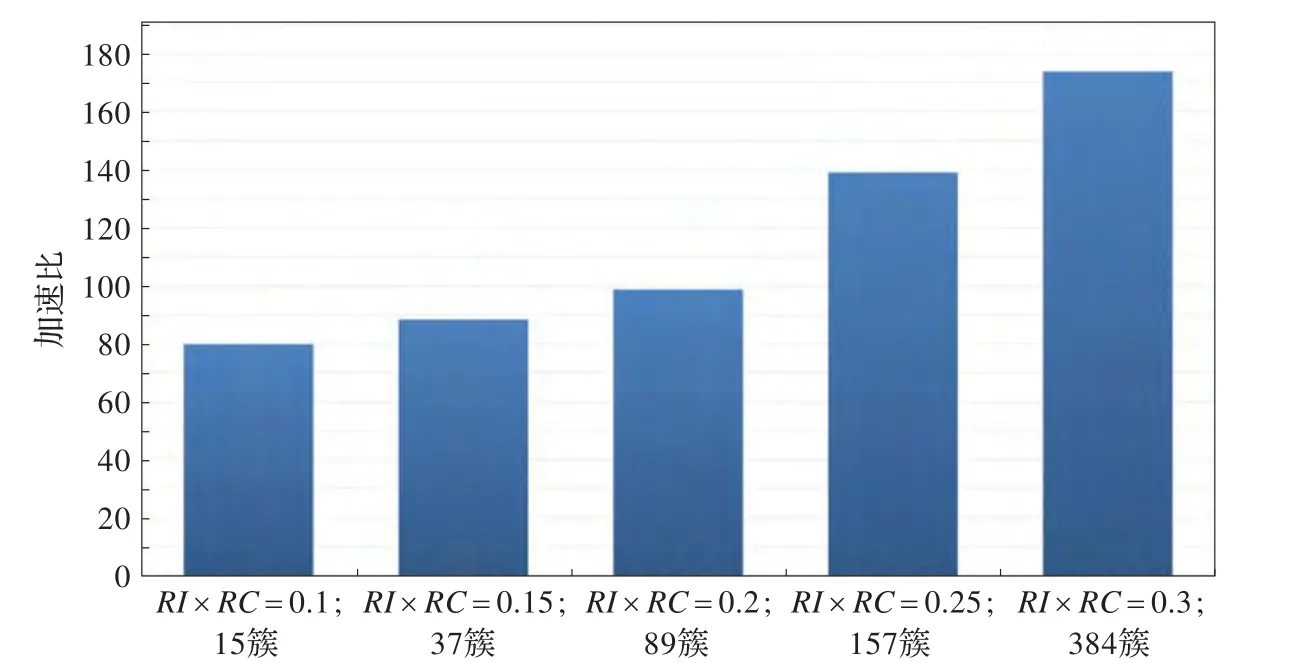
图13 AIK-Means算法总体的加速比
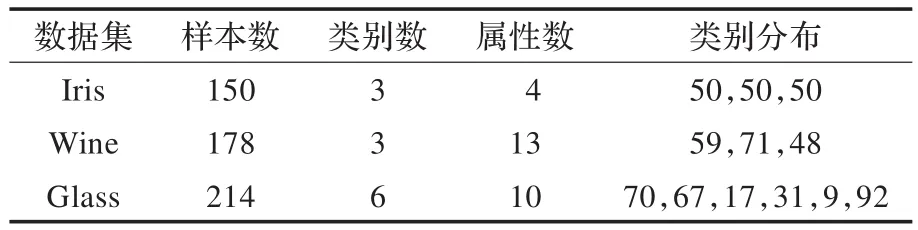
表2 数据及信息统计

其中表示Ci与第j类的交集大小。公式(7):
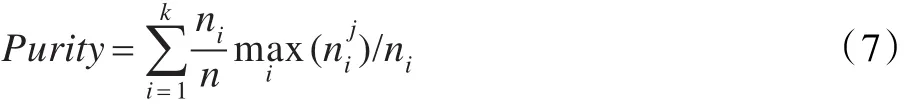
为整个结果的聚类纯度,k为最终形成的类簇数目,纯度越高,聚类算法越有效。本文将AIK-Means算法的迭代参数设定为50次,利用FP-Tree在这50次聚类结果中进行关联分析,得出最终聚类结果。如图14所示。
从图14可以看出,AIK-Means算法比传统的K-Means算法运行结果要好。
4 总结
在内存数据中,利用CUDA技术很好地加速了对内存数据的分析处理效率。在对心理学MMPI数据集的聚类实验中,AIK-Means算法在可接受的时间内执行多次,随着迭代次数的增加,算法的聚类纯度也随之提高,即执行效率的提高有效地支持了聚类纯度的提高。将AIK-Means算法应用到某集团心理学测试系统中,对单位员工的MMPI数据进行了聚类分析,帮助心理学工作者对测试人员进行准确的划分,达到了预期效果。
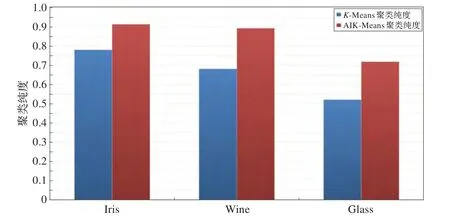
图14 聚类纯度的对比
[1]Bradley P S,Fayyad U M.Refining initial points forK-Means clustering[C]//Proceedings of the 15th International Conference on Machine Learning.San Francisco:Morgan Kaufmann Press,1998:91-99.
[2]Selim S Z,Alsultan K.A simulated annealing algorithms for the clustering problem pattern recognition[J].Pattern Recognition,1991,24(10):1003-1008.
[3]马超,练继建.基于聚类遗传算法的梯级水利枢纽短期电力调度优化[J].天津大学学报,2010,43(1):1-8.
[4]巩敦卫,蒋余庆,张勇,等.基于微粒群优化聚类数目的K-均值算法[J].控制理论与应用,2009,26(10):1175-1179.
[5]刘靖明,韩丽川,侯立文.基于粒子群的K均值聚类算法[J].系统工程理论与实践,2005,25(6):54-58.
[6]王纵虎,刘志镜,陈东辉,等.一种改进的粒子群优化快速聚类算法[J].西安电子科技大学学报:自然科学版,2012,39(5):61-65.
[7]薛胜军,潘吴斌.基于MapReduce的气象数据并行PK-Means算法[J].武汉理工大学学报,2012,34(12):139-141.
[8]Kumar N,Satoor S,Buck I.Fast parallel expectation maximization for Gaussian mixture models on GPUs using CUDA[C]//Proceedings of 11th IEEE International Conference on High Performance Computing and Communications.Piscataway:IEEE Computer Society Press,2009:103-109.
[9]Zhang Fan,Wang Zhangye,Yao Jian,et al.Accelerating the calculation of protein molecular field using GPU cluster[J].Journal of Computer-Aided Design&Computer Graphics,2010,22(3):412-419.
[10]Takahashi T,Hamada T.GPU-accelerated boundary element method for Hemholtz’equation in three dimensions[J].International Journal for Numerical Methods in Engineering,2009,80(10):1295-1321.
[11]Labaki J,Mesquita E,Ferreira S L O.The BEM on General Purpose Graphics Processing Unit(GPGPU):a study on three distinct implementations[C]//Proceedings of the 11th International Conference on Boundary Element Techniques XI.United Kingdom:EC Ltd Press,2010:316-323.
[12]杜新军,王莹.基于双线性对的Chameleon签名方案[J].软件学报,2007,18(10):2662-2668.
[13]聂小晶,邱昌建.焦虑症和抑郁症患者的MMPI对照研究[J].华西医学,2009,24(6):1356-1361.

