SCARA机器人模糊自适应滑模控制

许 凡，白瑞林，过志强，闫文才

1.江南大学 轻工过程先进控制教育部重点实验室，信息与控制实验教学中心，江苏 无锡 214122

2.无锡信捷电气有限公司，江苏 无锡 214072

1 引言

机器人作为复杂的多输入多输出非线性系统，具有时变、强耦合和非线性的动力学特征。传统的PID控制、计算力矩控制依赖精确的动力学模型，很难实现快速、高精度的机器人轨迹跟踪控制。近年来，很多学者结合诸如神经网络[1-2]、迭代学习控制[3-4]、模糊控制理论[5]提出了相关的机器人轨迹跟踪控制算法。神经网络、迭代学习控制在被控对象发生变化时，需要一个学习过程来调整控制策略，不适合快时变的被控对象；模糊控制由于模糊规则大多数取决于经验，存在局限性。

滑模变结构控制的滑动模态运动对系统的参数摄动、外界扰动、系统不确定具有不变性，且控制结构简单，因此非常适用于机器人轨迹跟踪控制。要改善滑模控制的动态品质，一方面要设计合理的滑模面：康宇[6]等提出了一种新的指数滑模面，加快了系统沿滑模面的收敛速度。Xinghuo Yu[7]等人设计了一种快速终端滑模面，实现了初始状态远离滑模面的快速收敛，但是存在奇异性。文献[8]设计了一种改进型的积分滑模面改善系统的跟踪速度和超调量。另一方面需要设计合理的趋近律：高为炳[9]提出了趋近律的概念，为缩短趋近过程时间以及削弱抖振提供了一个有效的方法。Charles J[10]等人在指数趋近律的基础上，设计了一函数代替恒定趋近系数，根据误差大小动态调节趋近系数；王燕[11]等提出了一种改进趋近律的快速非奇异终端滑模控制策略。席雷平[12]等提出了一种模糊幂次趋近律，在保证抖振抑制效果的前提下提高了系统的趋近速度。梅红[13]等提出了一种新的双幂次趋近律，使系统在趋近过程中有较高的速度，并消除了传统滑模的固有抖振。

本文从滑模控制器的滑模面和趋近律两个方面入手，对SCARA机器人滑模控制系统进行了设计。针对快速终端滑模面的奇异性进行改进，设计了一种非奇异的快速终端滑模面；对趋近律进行了改进，同时采用双曲正切函数替代传统的符号函数，有效地消除了抖振；通过自适应模糊控制调节趋近律参数，改善了初始状态力矩冲击问题。

2 SCARA机器人动力学模型

对于一个n关节的机器人系统，其动力学方程可以由以下二阶非线性微分方程描述[14]：

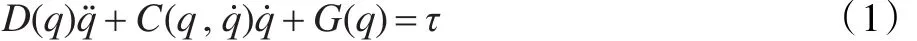
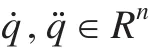
SCARA机器人如图1所示。利用拉格朗日方法，可以求出动力学模型[15]如下：

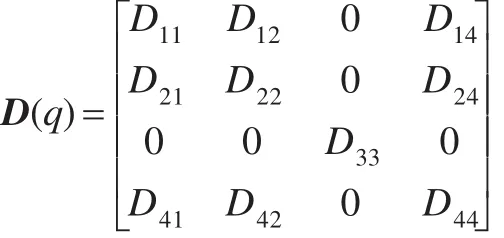
图1SCARA机器人

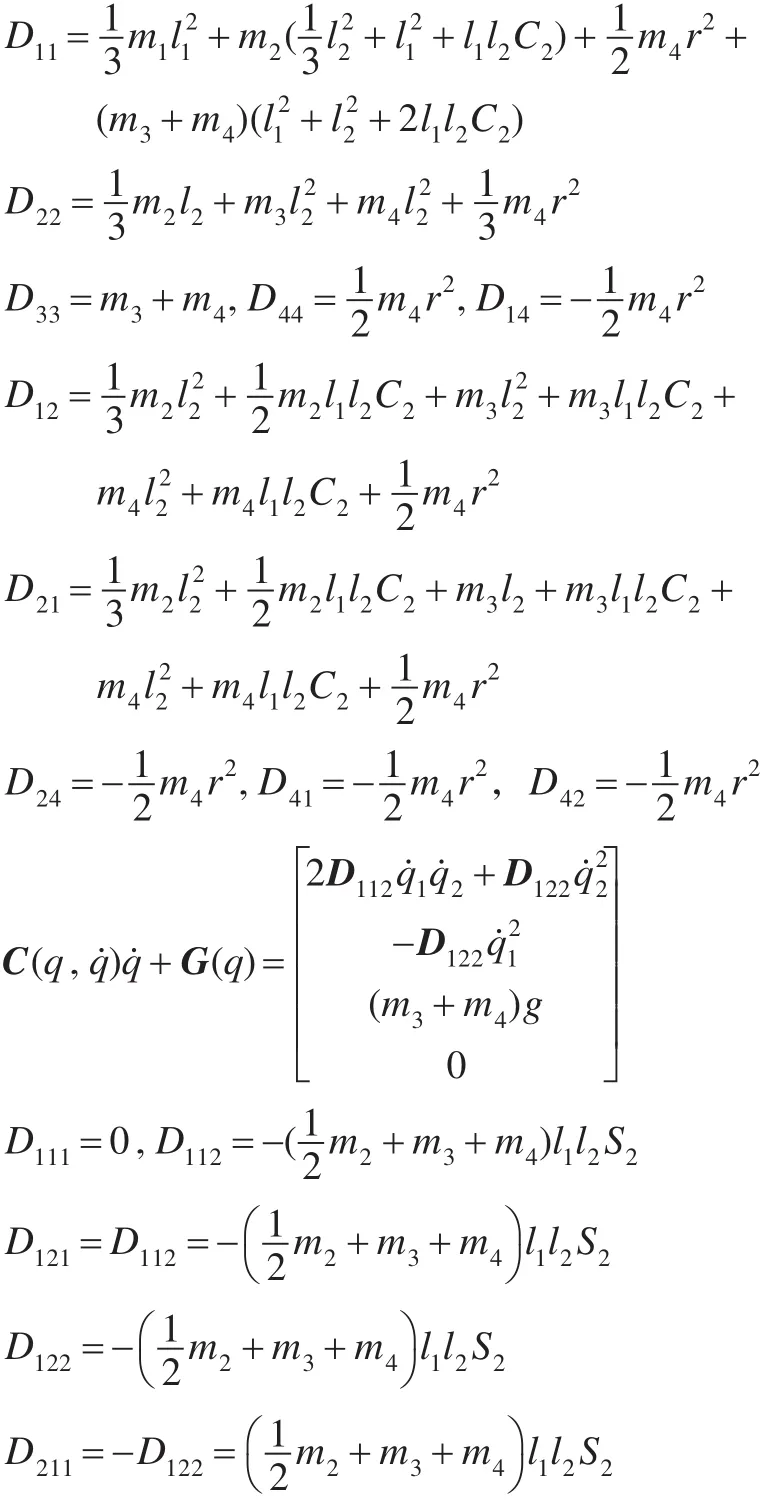
其中，mi代表各连杆的质量，li代表各连杆长度，Ci,Si是cos(qi),sin(qi)的简写。

3 非奇异快速滑模面的设计

滑模控制可分成趋近与滑模运动两个阶段。在滑模运动阶段，闭环系统的动态特性完全由滑动模态决定，系统表现出完全鲁棒性。常见的滑模面有：线性滑模面、终端滑模面，以及快速终端滑模面。其中快速终端滑模面的收敛速度最快：

式中参数α＞0,β＞0,2＞λ＞1。但是当状态变量小于零时，某些情况下可能存在指数项非实数的情况，从而无法在实数域到达滑模面，存在局限性。本文改进了快速终端滑模面：

将机器人关节位置跟踪误差e作为系统的状态变量，定义为：

式中qd为机器人期望的关节位置矢量；q为实际的关节位置矢量。则机器人控制系统的滑模面设计为：

式中为位置跟踪误差的导数。从式（5）知，对于任意状态变量，都不存在和的情况，弥补了式（2）的不足。

下面证明系统将在有限时间内达到平衡点：

令si=0，(i=0,1,…,n)当ei＞0时，由式（5）可得：

于是式（6）改写为：

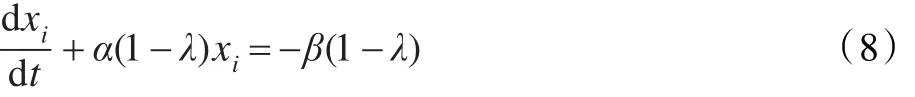
式（8）的通解为：

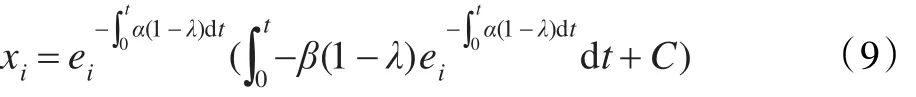
当t=0时，C=xi(0)则式（9）改写为：

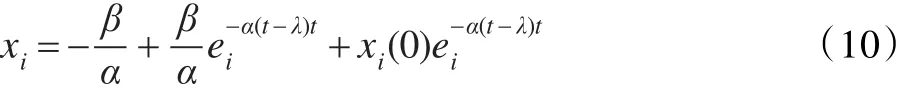
由于ei=0时，xi=0,t=tr代入式（10）可得：

可以求得当ei＞0时，系统从任意初始状态收敛到平衡状态ei=0的时间：

因此，该滑模面s能够使系统在有限时间内达到平衡点。当ei＜0时，同理可证。

4 滑模趋近律的设计

4.1 改进的滑模趋近律

滑模运动阶段的性能主要依靠滑模面的设计来保证，而趋近阶段的性能可以通过趋近律的设计来改善。常见的趋近律有：等速趋近律、指数趋近律、幂次趋近律。其中等速趋近律趋近速度恒定，不能灵活调节参数，且运动品质不够好；指数趋近律能够快速地趋近滑模面，但不能使系统从理论上消除抖振；幂次趋近律能够平滑地进入滑动模态，但是在远离滑模面时在快速性方面存在不足。

结合指数趋近律的快速性与幂次趋近律进入滑动模态的平滑性，设计如下的趋近律：

式中，0＜a＜1，h,k＞0。

趋近律式（13）分成两个部分，以|s|=1为界，当系统远离滑模面时(|s|＞1)趋近速度主要取决于式（13）的第一项；当系统接近滑模面(|s|≤1)时趋近速度主要取决于式（13）的第二项；则该趋近律既保证了远离滑模面时的快速性，也保证了接近滑模面的平滑性，所以在加快到达滑模面的速度的同时，也削弱了系统的抖振。

趋近律式（13）可达性的证明：

滑模控制可达性条件是：

式（13）的趋近律满足：

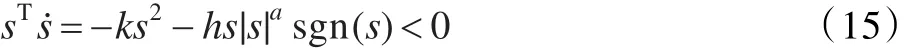
4.2 双曲正切函数改善系统高频抖振

为了进一步消除滑模控制系统的高频抖振，考虑采用双曲正切函数代替符号函数，其表达式为：

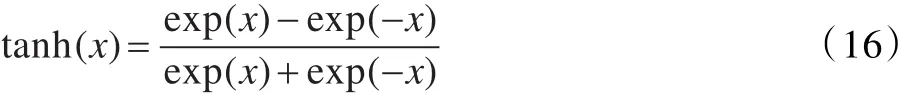
由图2可见，双曲正切函数相比于符号函数，随自变量趋近饱和的变化速度更平缓。同时，可以引入适当的增益系数，调整过零点的斜率，即趋近饱和的速度。用双曲正切函数可有效地消除高频抖振。所以将趋近律改进为：

其中h,k＞0,1＞a＞0,b＞1。

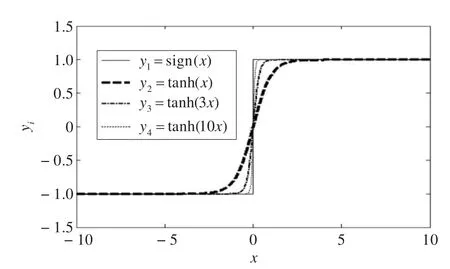
图2 符号函数与双曲正切函数曲线

4.3 趋近律系数的模糊自适应调整

机器人滑模控制系统在初始状态远离滑模面时有较大的误差和误差变化率，此时控制器会产生较大的输出力矩，对机器人系统造成很大的损害。为避免这种情况，对滑模控制的趋近律系数进行模糊控制，通过调节k来达到：当误差及误差变化率大的时候尽量减小k；反之，则增加k。

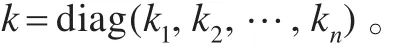
选择e,de,k的论域，将它们模糊化为7个等级，定义如下：

表示为{-3,-2,-1,0,1,2,3}，分别对应负大，负中，负小，零，正小，正中，正大。

建立ki的调整规则，具体的控制规则为：当ei或dei较大时，适当减小ki的值；当ei或dei较小时，则适当增大ki的值。

为使已有模糊控制器具有更强的应变性，采用控制规则可自调整的自适应模糊控制器。对于一个二维的模糊控制器，当其输入变量E、DE和输出量U的论域划分等级相同时，所引入的描述控制规则表达式为：

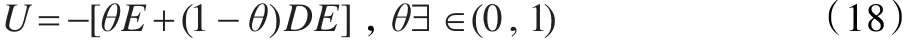
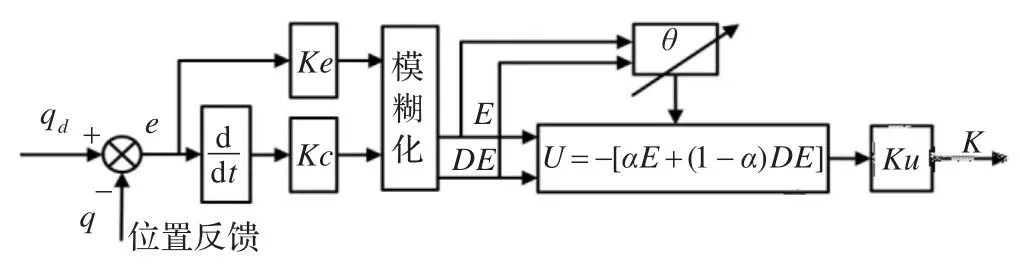
图3 趋律系数的自适应模糊调整

通过调节θ值便可以对控制规则进行调整。θ值的大小直接反应对误差E和误差变化率DE的加权程度。

5 SCARA机器人滑模控制律的设计

对式（5）进行微分可得：

将式（4）代入式（19）可得

由式（1）可知

将式（21）代入式（20）可得

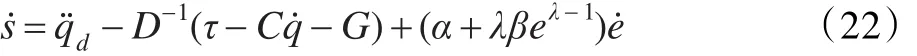
由式（22）和式（13）可知

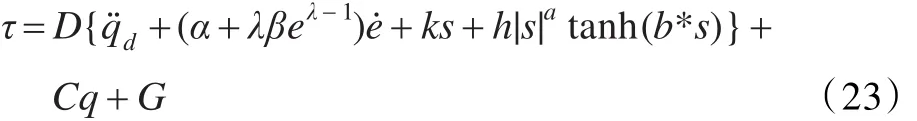
根据式（23）所描述的控制系统，如图4所示。

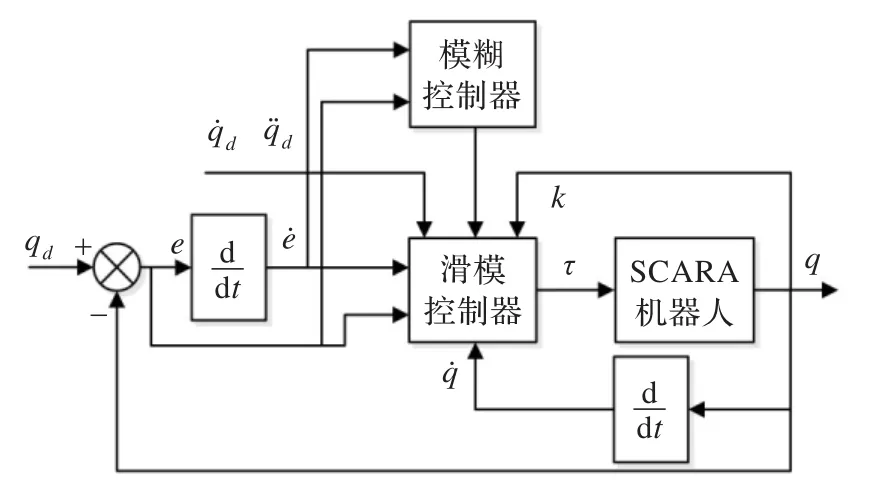
图4 控制器系统框图

6 实验测试与分析

SCARA机器人的物理参数如下：m1=15 kg,m2=12 kg,m3=3 kg,m4=3 kg,l1=0.5 m,l2=0.4 m,r=0.2 m,g=9.8 m/s2。

期望的跟踪轨迹：

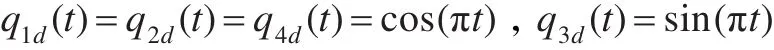
初始条件为：

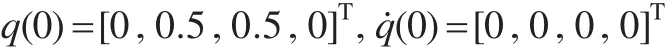
控制参数为：

α=5,β=1,λ=1.9,k=10,h=7,a=0.2,b=5,为方便说明本文控制算法的有效性，将本文的算法与方法（a）（线性滑模面+快速趋近律）、方法（b）（快速终端滑模面+指数趋近律）进行对比。

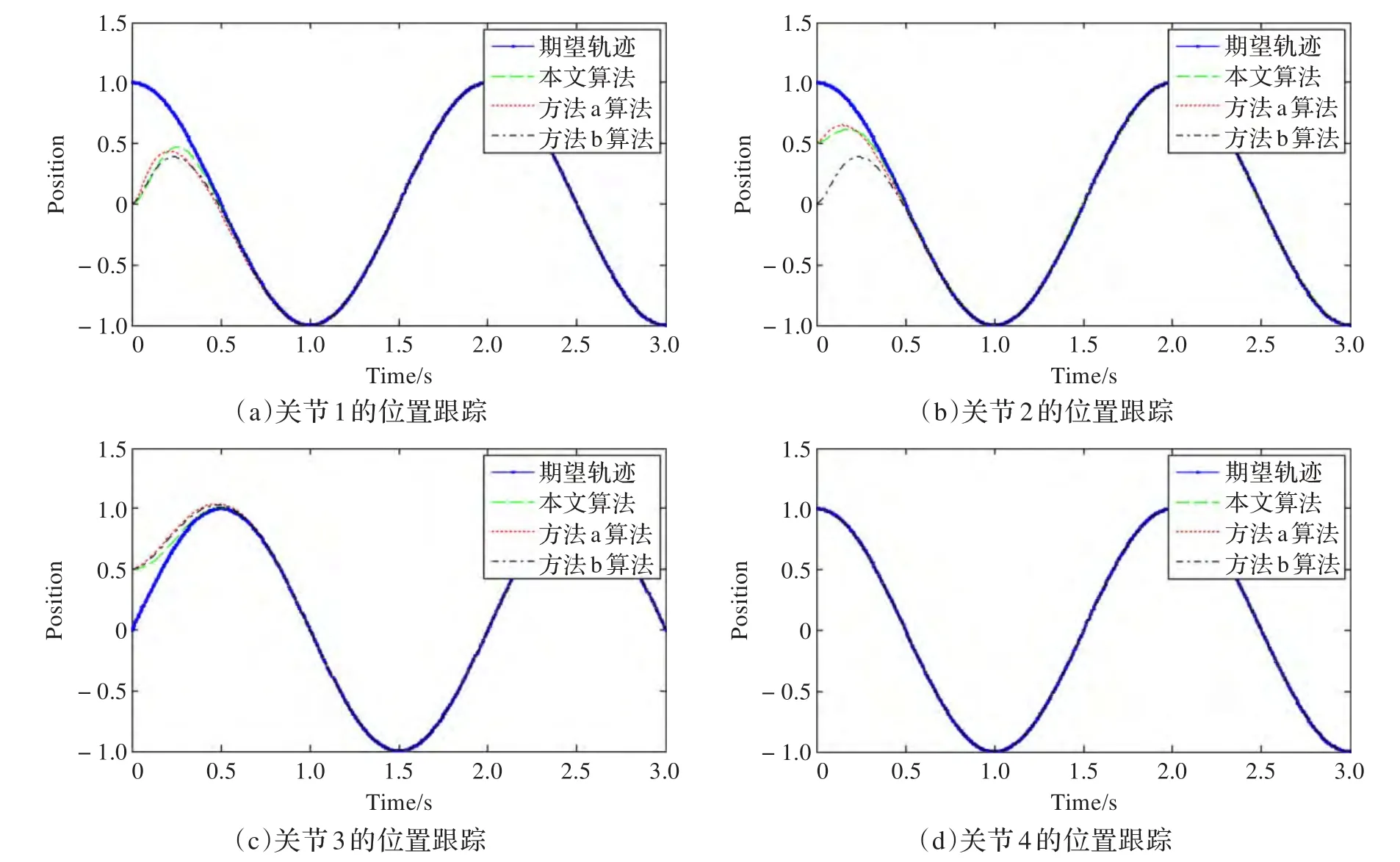
图5 位置跟踪

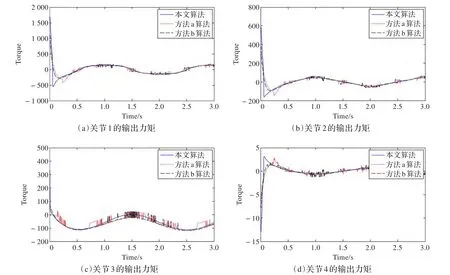
图6 输出转矩

仿真结果如图5、6所示。从图5的（a）、（b）、（c）可以看出，当初始误差不为零时，本文提出的非奇异快速终端滑模面结合改进的趋近律的滑模控制的跟踪速度比方法（a）、方法（b）的趋近速度快，从图5的（d）可以看出，在初始误差为零时，稳态误差接近零，有很好的跟踪效果。结合图5和图6可以看出，在保证跟踪速度的同时，改进的算法很好地消除了系统的抖振，同时降低了初始误差较大时的大力矩。由此可见，本文提出的算法在保留原有快速跟踪的同时，有效消除了抖振，降低了误差较大时的力矩冲击，提高了系统的控制性能。

7 结论

本文以工业上应用极为广泛的SCARA机器人为研究对象，进行了SCARA机器人的基于饱和函数的改进趋近律的模糊滑模机器人轨迹跟踪控制，并通过MATLAB分别对几种算法进行了仿真与对比试验。通过对比分析可知，该方法具有良好的控制性能。

针对快速终端滑模面的当状态变量为负时出现的奇异性，对快速终端滑模面进行了改进，有效提高收敛速度的同时，保证了系统的非奇异性。

结合了指数趋近律和幂次趋近律的优点，对滑模控制的趋近律进行改进，有效地提高了轨迹跟踪控制的收敛速度。

引入了双曲正切函数，代替滑模控制中的符号函数，有效地消除了高频抖振，并且可以通过调节增益系数，即过零点斜率。

采用模糊自适应控制器对趋近律中指数项的系数进行修正，改善了由于大范围的初始位姿偏差而引起的大力矩问题。

[1]Wai Rong-Jong，Yang Zhiwei.Design of fuzzy neural network tracking control with only position feedback for robot manipulator including actuator dynamics[J].Control Theory&Applications，IET，2010，6（2）：1079-1093.

[2]王良勇，杨枭.带有前馈和神经网络补偿的机械手系统轨迹跟踪控制[J].电机与控制学报，2013，17（8）：113-118.

[3]Kazemi H，Ahangarian S，Hashempour A.Fuzzy path tracking control of a 5-DOF experimental robot[J].Information and Automation，2008：436-440.

[4]刘国荣，张杨名.移动机器人轨迹跟踪的模糊PID-P型迭代学习控制[J].电子学报，2013（8）：1536-1541.

[5]Qiao Jihong，Dai Yaping，Liu Jinkun，et al.Robust adaptive fuzzy output tracking control of uncertain robot system using backstepping design[C]//Control Conference，2007：303-308.

[6]康宇，奚宏生，季海波.有限时间快速收敛滑模变结构控制[J].控制理论与应用，2004，21（4）：623-626.

[7]Yu Xinghuo，Man Zhihong.Fast termianl sliding-mode control design for nonlinear dynamical sytems[J].IEEE Transactions on Fundamental Theory and Applications，2002，49（2）：261-264.

[8]李鹏，孙未蒙，李文强.一种改进积分滑模面在飞控中的应用[J].控制工程，2010，17（3）：269-271.

[9]Gao W，Hung J C.Variable structure control of nonlinear system：a new approach[J].IEEE Trans on Industrial Electronics，1993，40（1）：45-55.

[10]Fallaha C J，Saad M，Kanaan H Y，et al.Sliding-Mode robot control with exponential reaching law[J].IEEE Trans on Industrial Electroics，2011，58（2）：600-610.

[11]王燕，芦逸云，葛运旺.基于趋近律的力矩电机终端滑模轨迹跟踪控制[J].华中科技大学学报，2013，41（4）：83-87.

[12]席雷平，陈自立，齐晓慧.具有抖振抑制特性的机械臂快速滑模变结构控制[J].电机与控制学报，2012，16（7）：97-102.

[13]梅红，王勇.快速收敛的机器人滑模变结构控制[J].信息与控制，2009，38（5）：552-557．

[14]蔡自兴.机器人学[M].2版.北京：清华大学出版社，2009.

[15]陆金伟，李跃民.SCARA机器人的完整动力学显方程的推导[J].振动、测试与诊断，1995，15（3）：23-29．