线性时不变系统特性的教学方法探讨

唐普英，陈鹏宇

(电子科技大学 a.光电信息学院;b.通信与信息工程，成都 610054)

·课程教学改革·

线性时不变系统特性的教学方法探讨

唐普英a，陈鹏宇b

(电子科技大学 a.光电信息学院;b.通信与信息工程，成都 610054)

线性时不变LTI系统是一种很重要的系统，它具有4个特性：无记忆性、因果性、稳定性和可逆性。按常用的信号与系统教材中介绍的方法讲授LTI系统特性，学生不容易理解所讲授的内容。授课过程中发现，若利用卷积和的交换律，把LTI系统的输出分为3个部分：与将来的输入有关的输出、与当前的输入有关的输出和与过去的输入有关的输出；然后根据LTI系统特性的定义，结合系统的输出与输入关系，先推导离散时间LTI系统的特性，再将其结论应用到连续时间LTI系统，则LTI系统特性教师既容易讲解清楚，学生也容易理解透彻，取得了良好的教学效果。

线性时不变系统系统; 系统特性; 离散时间; 连续时间

在信号与系统课程中，LTI系统是一类非常重要的系统。LTI系统具有4个特性：无记忆性、因果性、稳定性和可逆性。LTI系统又分连续的和离散的，按常用的信号与系统教材[1-6]中介绍的方法讲授LTI系统特性时，学生不容易理解所讲授的内容。

已知离散时间LTI系统的单位数字冲激序列响应为h[n]，若输入序列为x[n]，则系统的输出序列等于单位数字冲激序列响应h[n]和输入序列的卷积和x[n]*h[n],即：

x[-2]h[n+2]+x[-1]h[n+1]+x[0]h[n]+x[1]h[n-1]+x[2]h[n-2]+…

(1)

对于连续时间LTI系统，已知其单位冲激响应为h(t)，若输入为x(t)，则系统的输出信号等于x(t)与h(t)的卷积积分，即：

(2)

常用的信号与系统教材根据式(1)和式(2)的表示，就直接给出LTI系统特性对系统冲激响应h[n]或h(t)应该满足的条件，学生觉得不容易理解这些条件。授课过程中每次讲授到此部分内容时，总有学生提出疑问。

在教学过程中发现：若利用“卷积和”的交换律，则可以把式(1)的系统输出分为3个部分(如式(4)所示)：与将来的输入有关的输出、与当前的输入有关的输出和与过去的输入有关的输出。

实际上，利用“卷积和”的交换律，式(1)可以表示为：

y[n]=x[n]*h[n]=h[n]*x[n]=

(3)

把式(2)右边的“求和表达式”展开后，得到：

(4)

由式(4)可以很容易地识别出，LTI系统的输出由3个部分组成：第1部分是与将来的输入有关的输出；第2部分是与当前的输入有关的输出；第3部分是与过去的输入有关的输出。

然后根据LTI系统特性的定义，结合系统的输出与输入关系，先推导离散时间LTI系统的特性，其次再将其结论推广到连续时间LTI系统，则教师容易讲解清楚LTI系统特性，学生也容易理解这些特性。

1 LTI系统的无记忆性

根据LTI系统无记忆性的定义：若系统的输出仅仅与当前时刻的输入有关，则该系统是无记忆系统。也就是说：无记忆系统的输出与过去的输入，以及将来的输入均无关。那么LTI系统的无记忆性对系统的冲激响应的要求条件是什么？

从式(4)可以看出，为了使得系统的输出y[n]只与x[n]有关，则式(4)等号右边的第1部分和第3部分应该不出现，即要求：h[n]=0，n≠0。因此，离散时间LTI无记忆系统的输出y[n]=h[0]x[n]，其中h[0]表示某一参量，可用K来表示。所以离散时间LTI无记忆系统的输出也可以表示为y[n]=Kx[n]。故离散时间LTI系统的无记忆性应满足条件：

h[n]=Kδ[n]

(5)

式中，δ[n]表示离散时间的单位冲激信号。把上述结论推广到连续时间LTI系统，得到连续时间LTI系统的无记忆性应满足条件：

h(t)=Kδ(t)

(6)

式中，δ(t)表示连续时间的单位冲激信号。

2 LTI系统的因果性

根据LTI系统因果性的定义：若系统的输出与当前时刻的输入和过去的输入有关，或系统的输出仅与当前时刻的输入有关则该系统是因果系统。也就是说：因果系统的输出与将来的输入无关。那么LTI系统的因果性对系统的冲激响应有何要求？

从式(4)可以看出，为了使得系统的输出y[n]与将来的输入x[n]无关，则式(4)等号右边的第1部分应该不出现，即要求：h[n]=0，n<0，或h[n]=h[n]u[n]。因此，离散时间LTI系统的因果性应满足条件：

h[n]=h[n]u[n]

(7)

式中，u[n]表示离散时间的单位阶跃信号，把上述结论推广到连续时间LTI系统，得到连续时间LTI系统的因果性应满足的条件：

h(t)=h(t)u(t)

(8)

式中，u(t)表示连续时间的单位阶跃信号。

3 LTI系统的稳定性

根据LTI系统稳定性的定义：若当系统的输入有界时，系统的输出也有界，则该系统是稳定系统。那么LTI系统的稳定性对系统的冲激响应有什么要求？

(9)

即离散时间LTI系统的冲激响应是绝对可和的。

把上述结论推广到连续时间LTI系统，得到连续时间LTI系统的稳定性应满足的条件：

(10)

即连续时间LTI系统的冲激响应是绝对可积的。

4 LTI系统的可逆性

根据LTI系统可逆性的定义：若LTI系统对不同的输入得到不同的输出，则该系统具有可逆性。若具有可逆性的LTI系统的冲激响应是h[n]，可以找到该系统的逆系统的冲激响应h1[n]，则原系统与其对应的逆系统级联后的等效系统是一个恒等系统(逆系统的输出就等于原系统的输入，如图1所示)。那么LTI系统的可逆性对系统的冲激响应的要求是什么？

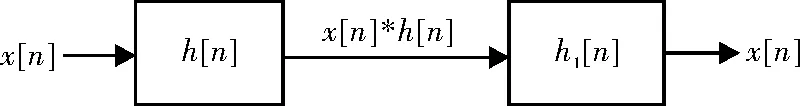
图1 LTI系统可逆性的表示

h[n]*h1[n]=δ[n]

(11)

把上述结论推广到连续时间LTI系统，得到连续时间LTI系统的可逆性应满足的条件：

h(t)*h1(t)=δ(t)

(12)

5 结束语

利用“卷积和”的交换律，把离散时间LIT系统的输出分为3个部分，然后根据LTI系统特性的定义，则比较容易讨论清楚LTI系统的特性。为了能使学生容易理解和接受相关的教学内容，就需要教师吃透教材，经过对知识的深度加工处理，从学生的角度出发，整理出学生容易理解和接受的知识。这是对教师的最基本要求。

[1]OPPENHEIMAV,WILLSKYAS,NAWAHHS.SignalsandSystems[M].2ndEdition.北京：电子工业出版社，2002.

[2] 郑君里，应启珩，杨为理. 信号与系统[M].2版.北京：高等教育出版社，2000.

[3] 陈后金，胡健，薛健. 信号与系统[M].北京：高等教育出版社，2007.

[4] 闵大镒，朱学勇. 信号与系统分析[M].成都：电子科技大学出版社，2000.

[5] 吕幼新，张明友. 信号与系统[M].北京：电子工业出版社，2007.

[6] 张小虹. 信号与系统[M].2版.西安：西安电子科技大学出版社，2008.

Exploration of Teaching Method on the Characteristics of Linear Time-Invariant System

TANG Puyinga,CHEN Pengyub

(a.School of Optoelectronic Information;b.School of Communication and Information Engineering,University of Electronic Science and Technology of China, Chengdu 610054, China)

Linear time-invariant (LTI) system is a kind of important system. It has four characteristics such as memoryless, causality, stability and invertibility. Students are not easy to understand the system characteristics taught by teachers according to the frequently-used “Signals and Systems” textbooks. It is shown that the output of LTI system can be divided into three parts, which are the outputs related to the future inputs, the outputs related to the current input, and the outputs related to the past inputs, if the commutative property of the convolution sum is used. The characteristics of the discrete-time LTI system are derived first, and the conclusion is applied to the continuous-time LTI system according to the definitions of the LTI system characteristics associated with the relationship between system outputs and system inputs. The characteristics of LTI system can be easily taught by teachers, and easy understand by students. The good teaching effect has been achieved.

LTI system; system characteristic; discrete time; continuous time

2015-01-15；修改日期:2015-02-25

电子科技大学教学改革研究项目(2013 XJYSL011)。

唐普英(1965-), 男, 博士, 副教授, 主要从事电子技术的教学与研究工作。

A

10.3969/j.issn.1672-4550.2015.06.056