随机噪声对海洋布里渊激光雷达测量的影响
随机噪声对海洋布里渊激光雷达测量的影响
王元庆1,何炬2,马泳1,余寅1,张念1,梁琨1*
(1.华中科技大学 电子与信息工程系, 武汉 430074; 2.华中光电技术研究所 武汉光电国家实验室,武汉 430074)
摘要:为了分析激光雷达系统中随机噪声对海水布里渊散射谱以及温度反演精度的影响,依据布里渊散射理论及系统噪声特性,对带噪布里渊散射频谱进行了理论分析,并进行了信噪比从1dB~100dB的仿真实验。结果表明,当信噪比大于16dB时,频移和线宽的平均误差和不确定度能够控制在兆赫兹量级,温度误差和不确定度能够控制在0.2℃以内;采用实际应用中多次测量取平均的方法,10次平均能够保证0.2℃的测量精度对信噪比的要求下降到7dB。这为激光雷达在海水高精度遥感提供了指导。
关键词:激光技术;海洋布里渊散射;随机噪声;频移;线宽;温度;测量误差
*通讯联系人。E-mail:liangkun@hust.edu.cn
引言
采用布里渊散射信号检测技术进行海洋探测始于20世纪 60 年代。随着激光及其相关技术的发展,采用布里渊激光雷达系统进行海洋环境的监测已得到了广泛的应用[1-2]。在这些应用中,精确地获取布里渊散射回波信号光谱对于海洋环境参量的测量来说是非常重要的。目前,获取回波信号的方式主要有3种:边缘探测技术[3]、扫描式法布里-珀罗(Fabry-Pérot, F-P)干涉仪[4]、F-P标准具结合增强型电荷耦合器件(intensified charge coupled device,ICCD)[5]。在这些方法中,F-P标准具结合ICCD的方法以其能够在很短的时间内获得完整的布里渊谱而得到广泛的应用和深入的研究[6-7]。
F-P标准具接收到的回波信号在ICCD上呈现为一幅2维干涉圆环图,从中提取到的干涉光谱能够用于获取布里渊散射光谱,通过测量该散射光谱能够获得布里渊频移和线宽,进而反演得到海水的温度、盐度等参量[3,8]。在该过程中,ICCD上的噪声会污染所得到的干涉光谱,是影响测量结果精度的一个重要因素。该噪声主要包括暗电流噪声和散粒噪声两个部分。暗电流噪声是由ICCD硅衬底上的热电子引起的,该噪声比较平稳,可以表示成一个固定值。它只会对光谱线形进行整体抬升,并不影响谱线线形,对于频移和线宽等谱特征参量的测量来说,并不会造成影响。散粒噪声是光的量子特性的根本表现,是从物体发射的光子数目统计波动中反映出来的。该噪声幅度与ICCD每一个像素接收到的光子数即信号强度有关,是一种服从泊松统计的随机噪声。与暗电流噪声相比,散粒噪声会严重影响接收到的光谱谱线的线形,它不但是造成测量误差的主要因素,而且其随机性会使得同一条件下每次测量的结果都不同,造成测量结果的不确定性。因此,分析散粒噪声带来的影响对精确测量海水特性物理参量有重要的意义。
作者的目的是根据散粒噪声的特性来分析该噪声对谱特征参量测量以及海水参量反演的影响。首先理论分析接收到的布里渊散射回波信号以及ICCD噪声的特性。进一步地,结合这些信号与噪声的特性,仿真分析同一幅度噪声的随机性带给测量上的不确定程度,以及不同幅度的噪声对布里渊频移和线宽测量的影响。最后,通过测得的布里渊频移和线宽来反演温度,将温度与已知条件相比较,最终评估ICCD噪声对温度反演的影响,从而为布里渊激光雷达的高精度海洋遥感提供服务。
1理论验证
当激光进入水中时,入射光子会与因水密度波动产生的声模相互作用,从而会产生后向布里渊散射现象。当后向散射光进入F-P标准具时,它会被标准具的两个反射面分成多个光束,当这些光束通过聚焦透镜聚焦,就会产生干涉现象并在增强型电荷耦合器件ICCD上呈现出干涉圆环图像。这个过程如图1所示。
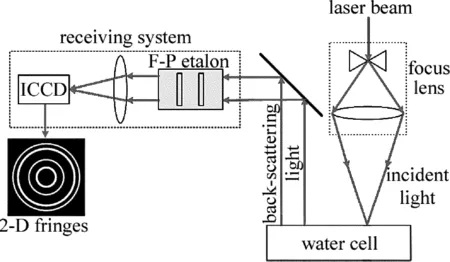
Fig.1 Scheme of Brillouin lidar system using F-P etalon and ICCD
干涉圆环图像上距离圆环中心为r处点的强度值Irec(r)可以表示为布里渊散射光频谱I(ν)与F-P标准具的器件函数A(ν,r)的卷积[9]。即:

式中,ν是散射光的频率。布里渊频谱I(ν)由两个峰组成,可以用两个洛伦兹函数表示[9]:
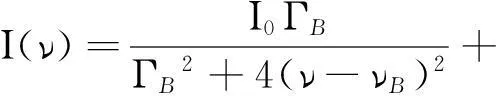

式中,I0是峰值的最大值,νB是布里渊峰中心到相邻瑞利峰中心的频率偏移,称为布里渊频移,ΓB是布里渊峰的半峰全宽(full width at half maximum,FWHM),称为布里渊线宽。I(ν)中前一部分表示散射中的斯托克斯分量,后一部分表示反斯托克斯分量。两种分量对称地分布在激光中心频率两旁,其幅值以及线形函数相同。F-P标准具的仪器函数A(ν,r)可以表示如下:
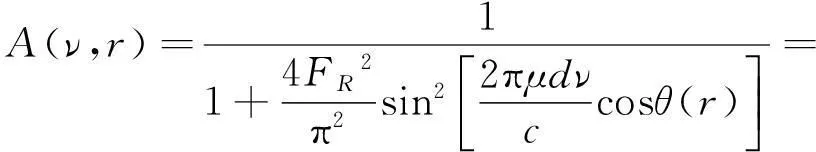
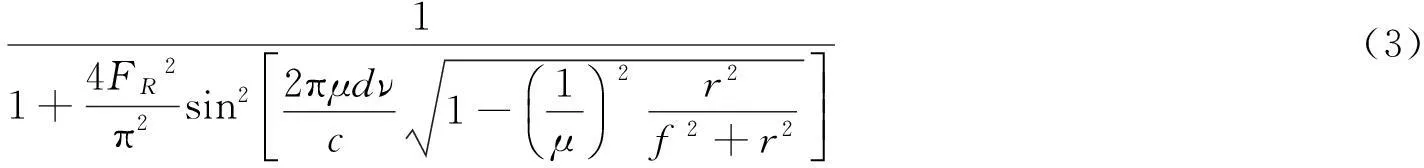
式中,μ是F-P标准具腔内介质的折射率,d是F-P标准具的腔长,c为光速,f是F-P标准具后面聚焦透镜的焦距,该透镜用来在ICCD上聚焦F-P标准具产生的平行光,用于ICCD端成像,θ是光在标准具中的折射角,FR=πR1/2/(1-R)为F-P标准具的精细度,其中的R为F-P标准具的反射率。F-P标准具的腔长d是固定的,可以通过改变折射角θ来改变频率ν,θ与半径r有关,不同的半径r处呈现出不同的频率ν,因而F-P标准具的器件函数也可以由(3)式中第2个等号后边的式子表示。由(1)式能够仿真得到的ICCD输出的纯信号图像,如图2所示。

Fig.2 Schematic of 2-D interference fringe pattern
图2中包含3级完整的条纹,每级条纹包含3个圆环:中间比较亮的是瑞利散射圆环,该圆环所处的位置对应于干涉谱上激光中心频率的位置。在其内外相对较暗的两条干涉圆环分别是布里渊散射的反斯托克斯分量和斯托克斯分量。
ICCD输出干涉圆环图像时会附带产生噪声。DUSSAULT等人的研究工作给出ICCD上的噪声Nn主要分为两个部分:暗电流噪声Ns和散粒噪声Nr,如下式所示[10]:

暗电流噪声Ns是在以硅为衬底的ICCD中热产生的电子引起的,与每一个ICCD像素的特性相关,该噪声是一个固定噪声,可以表示为一个常数。对于一个干涉谱图像来说,Ns可以表示为图像灰度值的总体抬升。散粒噪声Nr是量子光的基本属性,来源于物体发出光子数量的统计上的波动。DUSSAULT等人论证了该噪声的强度服从泊松分布[10]:

式中,G是总体电子增益,F是在得到噪声过程中引入的噪声因子,η是量子效率,用于表征在给定波长下的光电子产生过程,φp表示每一个像素的平均入射光子通量,τ是以s为单位的积分时间。该噪声与每一个像素的强度相关,表现为随机噪声。ICCD输出的干涉图像上每个像素的强度为信号Irec(r)与噪声Nn的叠加,如下式所示:

由(6)式可知,经由F-P标准具和ICCD接收到的布里渊干涉图样主要受到上述噪声的影响。而对于布里渊干涉谱来说,暗电流噪声只会对干涉谱进行整体抬升,不会影响干涉谱的线形;而随机噪声的幅度与每一个像素接收到的光子数即信号强度有关,它对干涉谱线形的影响主要表现在两个方面:一方面,信号越强噪声幅度越大;另一方面,由于随机噪声体现的是光子数量的统计波动,因此表现为整数个光子数量的强度,当整体接收到的光子数过少时,该噪声相对于信号的强度会变大,从而使线形变得更加粗糙,导致后续测量受到影响。因此,为了衡量噪声幅度对后续信号检测及测量的影响,以布里渊干涉图样上的信噪比(signal-to-noise ratio, SNR)RSNR来数学地表示噪声大小,如下式所示:
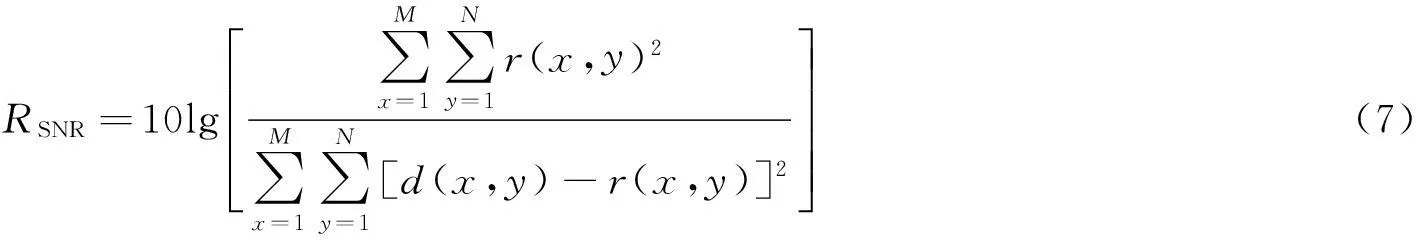
上式是针对一幅大小为M×N的图像来计算的,其中r(x,y)是没加噪时的图像数据,d(x,y)是加噪后的图像数据,其中的x代表数据的行,y代表数据的列。当噪声大时,RSNR会变小,图像会变得更粗糙。反之RSNR会变大,图像中信号将更加清晰。在下一章节中,作者将通过RSNR来说明噪声的幅度对测量的影响。
2仿真分析
为了说明噪声幅度对测量的影响,作者将通过仿真来模拟不同RSNR情况下的干涉谱。由理论部分的分析可知,ICCD接收到的干涉谱主要包括两个部分:回波信号和系统噪声。其中回波信号可用(2)式~(4)式产生,随机噪声可用(6)式产生,暗电流噪声是固定值,是根据以往的实验分析[9]经验性地获得。图3是温度为10℃的清水中,采用180°后向散射获得的布里渊干涉圆环图像,其中图3a~图3d的RSNR分别为0dB,10dB,20dB及30dB。产生干涉圆环图像所需要的实验条件如表1所示。

Fig.3a—interferenceringimageswhenRSNR=0dBb—interferenceringimageswhenRSNR=10dBc—interferenceringimageswhenRSNR=20dBd—interferenceringimageswhenRSNR=30dB
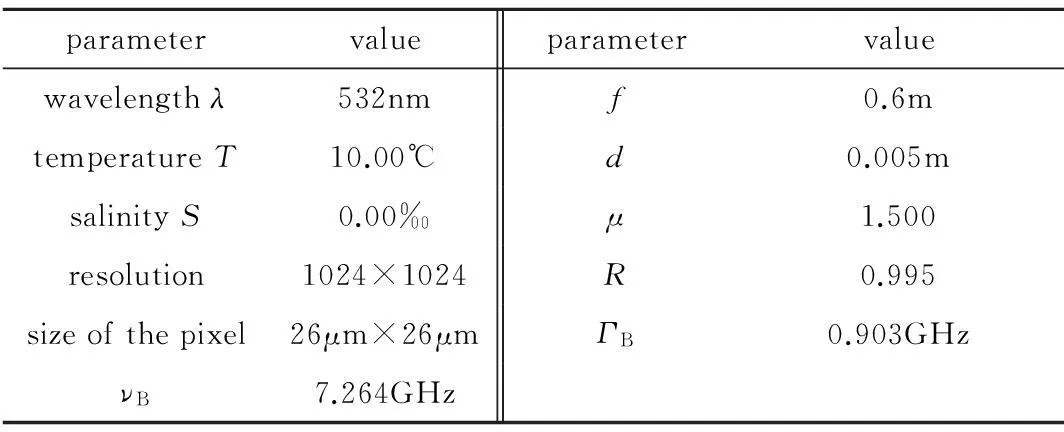
Table 1 Initial parameters when calculating the interference pattern
表1中所示参量是根据参考文献[11]中提到的实验装置来选取的。其中的布里渊频移νB和线宽ΓB是在设定的温度T和盐度S下根据参考文献[8]中提到的方法计算出来的。
通过图3可以看出,图中所示的图像相对于图1来说对比度更低,这是由于暗电流噪声引起的。同时,图3中随着RSNR增大,圆环轮廓变得越来越清晰,这主要是因为信号强度相对噪声来说越来越大。
图3中每一幅干涉圆环图像都包含有布里渊散射光谱的信息,可以用来获得布里渊干涉光谱并测量频移和线宽。作者曾在参考文献[12]中介绍了一种从2维干涉圆环中提取高分辨率光谱图的方法,称为数据折叠方法。该方法充分利用了2-D干涉圆环图像的像素信息,从而增加了谱线上的数据密度,使得图像分辨率达到1/100像素,达到了兆赫兹量级的光谱分辨率。以图3c中RSNR=20dB的干涉图为例,由该方法提取到的干涉光谱如图4中浅色线所示。
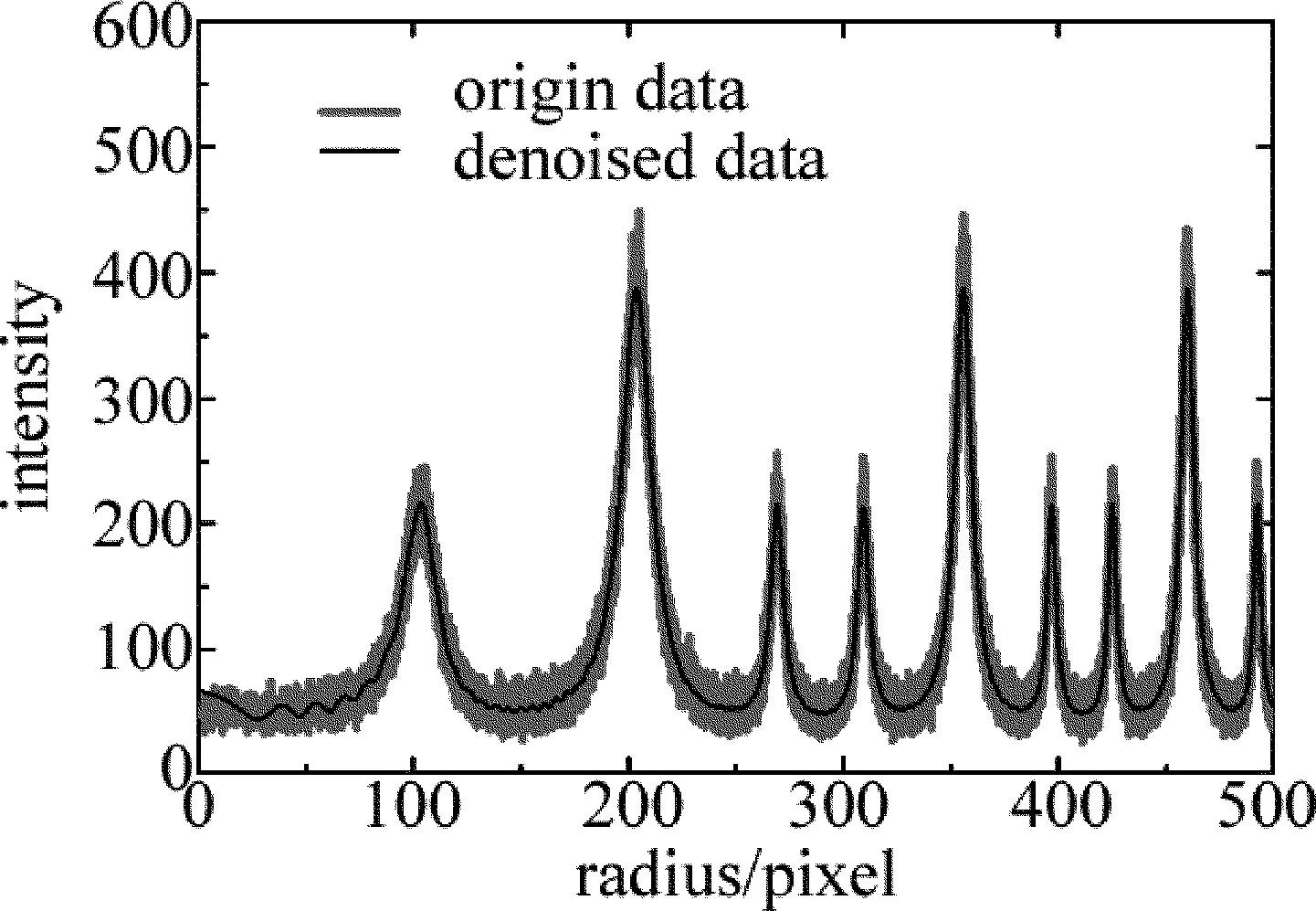
Fig.41-D interference spectrum extracted from Fig.3c and the denoised interference spectrum
从图4可以看出,噪声使干涉光谱变得粗糙。如果直接利用折叠后的数据进行拟合,测得对应的频移与线宽相差比较大,无法满足MHz测量精度的要求。因此,为了在一定程度上抑制噪声过大带来的影响,作者首先对带噪信号进行一次滤波。滤波过程采用的是一个基于频域的理想低通滤波器[12],对折叠后的数据进行滤波,滤波后的曲线如图4中深色曲线所示。
为从谱线上测量出布里渊频移和线宽,对去噪后的干涉光谱(如图4深线所示)进行拟合。拟合所采用的方法为Levenberg-Marquardt拟合算法,得到的布里渊频移和线宽拟合结果如表2所示。表2中νB,f为拟合计算得到的频移值,TνB,f为νB,f反演得到的温度[8],ΓB,f为拟合得到的线宽,TΓB,f为ΓB,f反演得到的温度[1]。
Table 2Parameters with interference spectrum undenoised and denoised respectively calculated frequency shiftνB,f, temperatureTνB,f,linewidthΓB,f, temperatureTΓBf(RSNR=20dB, theory frequency shiftνB=7.264GHz, theory linewidthΓB= 0.903GHz, theoretical temperatureT=10℃)

νB,f/GHzTνB,f/℃ΓB,f/GHzTΓB,f/℃undenoised7.51825.890.94654.92denoised7.26510.080.9049.98
从表2中可以得出,与初始值νB=7.264GHz以及ΓB=0.903GHz相比,未去噪的干涉谱拟合得到的频移值与理论频移值相差在几百兆赫兹,拟合得到的线宽与理论线宽值相差43MHz,频移与线宽反演得到的温度分别与理论值相差在15.89℃和44.92℃;而经过去噪后拟合出的频移νB,f与实际给定的相差1MHz,计算得出对应的温度与实际设定的温度相差0.08℃;拟合的线宽ΓB,f与实际给定的相差1MHz,计算得出对应的温度与实际设定的温度相差-0.02℃,拟合得到的频移与线宽都在兆赫兹量级,计算得出的温度误差在0.1℃以内。这说明通过去噪方法能够得到比较准确的结果。
然而,在加噪的过程中,由于所加的散粒噪声具有随机性,使得相同RSNR情况下的多次测量结果不稳定。为了验证这种不确定性并评估加噪的随机性性对结果带来的误差,作者对RSNR=20dB时重复加噪过程100次,结果如图5所示。
从图5a中可以看出,RSNR基本围绕在20dB上下浮动,浮动值约为0.02dB,说明加的噪声较为稳定;从图5b中可以看出,布里渊频移基本上围绕在7.264GHz上下浮动,浮动值约为5MHz;从图5c中可以看出,布里渊线宽基本上围绕在0.901GHz上下浮动,浮动值约为10MHz。这说所加噪声的随机性会导致RSNR的浮动,从而导致频移和线宽的浮动,即噪声的随机性会导致结果的不确定性。为进一步分析这种不确定性的大小,作者列出了这100次布里渊频移和线宽的均值及频移和线宽平均值对应的温度、100次结果得到的频移和线宽的不确定度及其不确定度对应的温度,如表3所示。其中,νB,ave为重复加噪100时拟合所得布里渊频移的平均值,TνB,ave为νB,ave反演对应的温度,δνB为加噪100次频移的不确定度,δTνB为不确定度δνB对应的温度,ΓB,ave为重复加噪100时,拟合所得布里渊线宽的平均值,TΓB,ave为ΓB,ave反演对应的温度,δΓB为加噪100次线宽的不确定度,δTΓB为不确定度δΓB对应的温度。
由表3可以看出,频移平均值与给出的理论值相同,线宽平均值与理论给出的相差了-2MHz,频移和线宽的不确定度在5MHz范围内,频移平均值反演得到的温度与理论值相同,线宽平均值反演得到的温度与理论值相差0.04℃,这表明在RSNR为20dB时,经过100次平均,平均值与理论值相差在兆赫兹量级,对应的温度与理论温度相差在0.1℃以内。同时频移和线宽对应的不确定度也都小于5MHz,说明单次测量产生的偶然性误差是在可接受范围内,也说明在RSNR=20dB时,单次测量能够从2维干涉圆环图像中得到较为准确的结果。
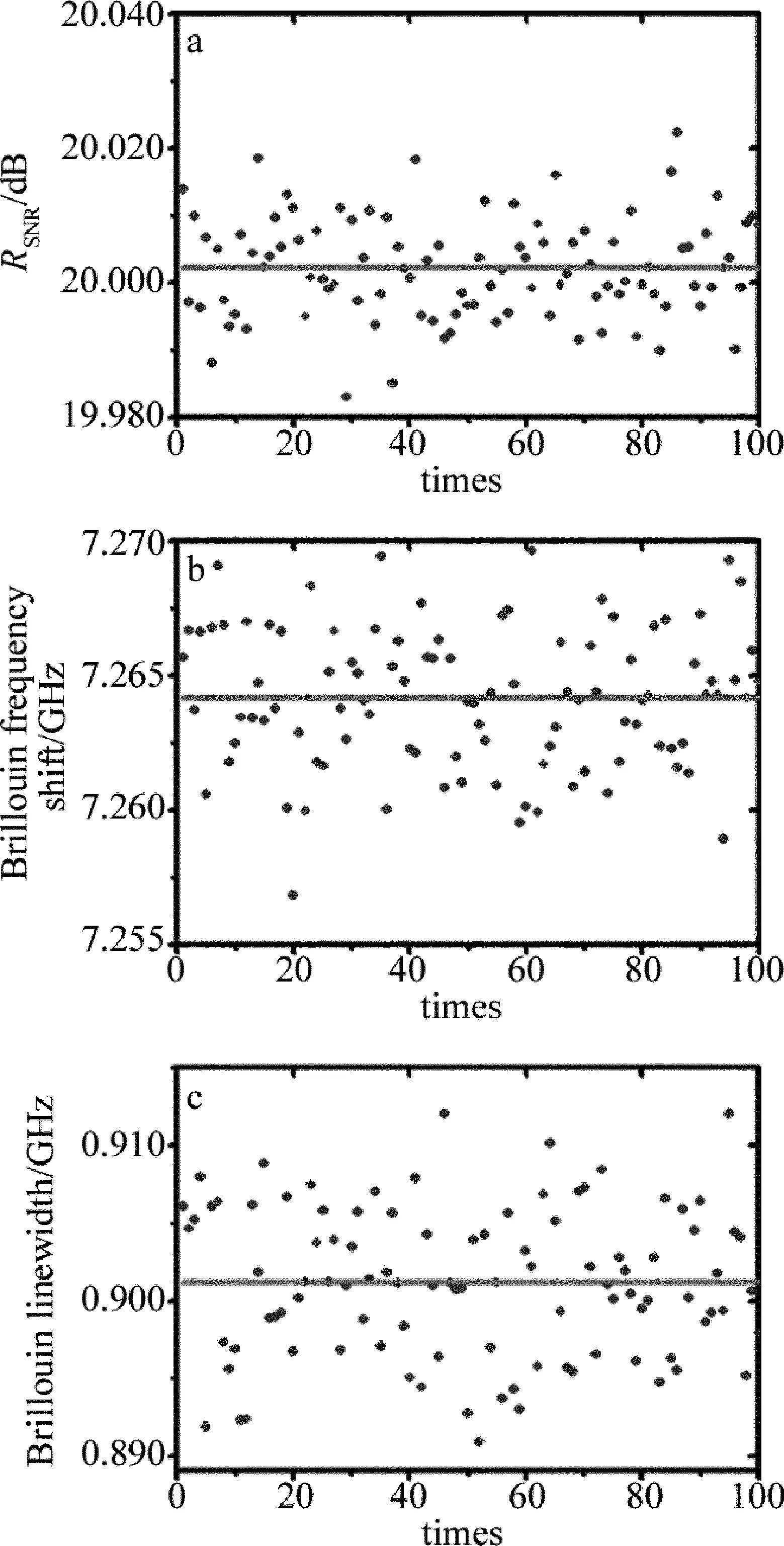
Fig.5a—the calculatedRSNR(dot)while repeating the procedure of adding noise 100 times whenRSNR=20dB and its average value(line)b—the calculated Brillouin frequency shift (dot)while repeating the procedure of adding noise 100 times whenRSNR=20dB and its average value(line)c—the calculated Brillouin linewidth (blue dot)while repeating the procedure of adding noise 100 times whenRSNR=20dB and its average value(line)
Table 3The average frequency shift and linewidth with their corresponding temperatures, the uncertainty of the results of 100 times and its corresponding temperature whenRSNR=20dB
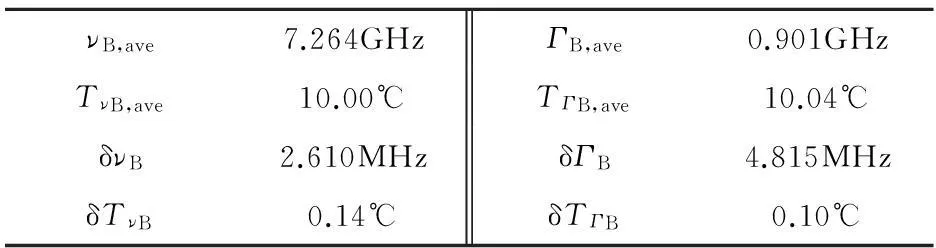
νB,ave7.264GHzΓB,ave0.901GHzTνB,ave10.00℃TΓB,ave10.04℃δνB2.610MHzδΓB4.815MHzδTνB0.14℃δTΓB0.10℃
同样,为了验证不同噪声大小对误差以及不确定度的影响,作者对不同RSNR的噪声进行了仿真,其中RSNR范围为1dB到100dB,每个dB重复了100次的加噪和测量过程,得到的结果如图6所示。图中深色点线为每个dB下100次测量结果的平均值。
从图6a和图6b可以看出,RSNR越小,实验结果产生的波动越大,达到数十到上百兆赫兹的波动范围。这说明噪声的随机性对测量结果确实产生了不确定性的影响。随着RSNR的增大,测量的不确定性逐步减小,当RSNR≥16dB时,频移的不确定度下降到5MHz以内,线宽的不确定度下降到10MHz以内。从图6c和图6d中可以看出,二者对应的温度不确定度在0.2℃范围内,此时的单次测量才能够用于高精度的温度测量应用中。对于这种随机性产生的测量不确定性,一个较好的方法是进行多次测量取平均。如图6中深色点所示,为各个RSNR下100次重复加噪测得结果的平均值。从该平均值来看,各个RSNR下的频移平均值与理论值最大的误差仅在5MHz范围内,而线宽平均值与理论值相差也在10MHz范围内,二者对应的温度误差在0.2℃范围内,这说明噪声的随机性虽然会对单次测量造成较大影响,但随着测量次数的增加,该随机性不会从统计上对其测量结果造成整体偏差。因此,采用多次测量取平均能够有效地降低随机性带来的影响,使精确测量对于谱线RSNR的要求降低。
然而,在真实测量应用中,由于多次测量耗时过多,往往不会对每次测量都重复进行100次,但可以满足重复测量10次的要求,因此,为了分析10次测量对测量精度的提升情况,作者对1dB~100dB的带噪谱进行了10次测量取平均,频移和线宽的测量结果如图7所示,其中浅色的点为每次测量的结果,深颜色的点为10次平均的结果。
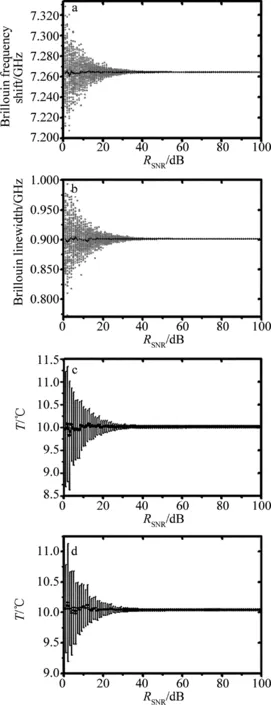
Fig.6a—the calculated frequency shift (dot) of each dB repeated 100 times withRSNRfrom 1dB to 100dB and their average value (dot-line)b—the calculated linewidth (dot) of each dB repeated 100 times withRSNRfrom 1dB to 100dB and their average value (dot-line)c—the corresponding temperatures (dot-line) and uncertainties (dark line) of the average frequency shift of Fig.6a withRSNRfrom 1dB to 100dBd—the corresponding temperatures (dot-line) and uncertainties (dark line) of the average linewidth of Fig.6b withRSNRfrom 1dB to 100dB
从图7a和图7b可看出,当RSNR≥7dB时,10次平均计算的布里渊频移和线宽的平均值与理论频移值相差均小于5MHz,频移平均值与线宽平均值对应的温度与理论温度值相差都小于0.2℃。这说明经过10次平均,能够降低对得到2-D干涉圆环图像RSNR的要求,在相同RSNR条件下能够有效地提高测量结果的准确度。
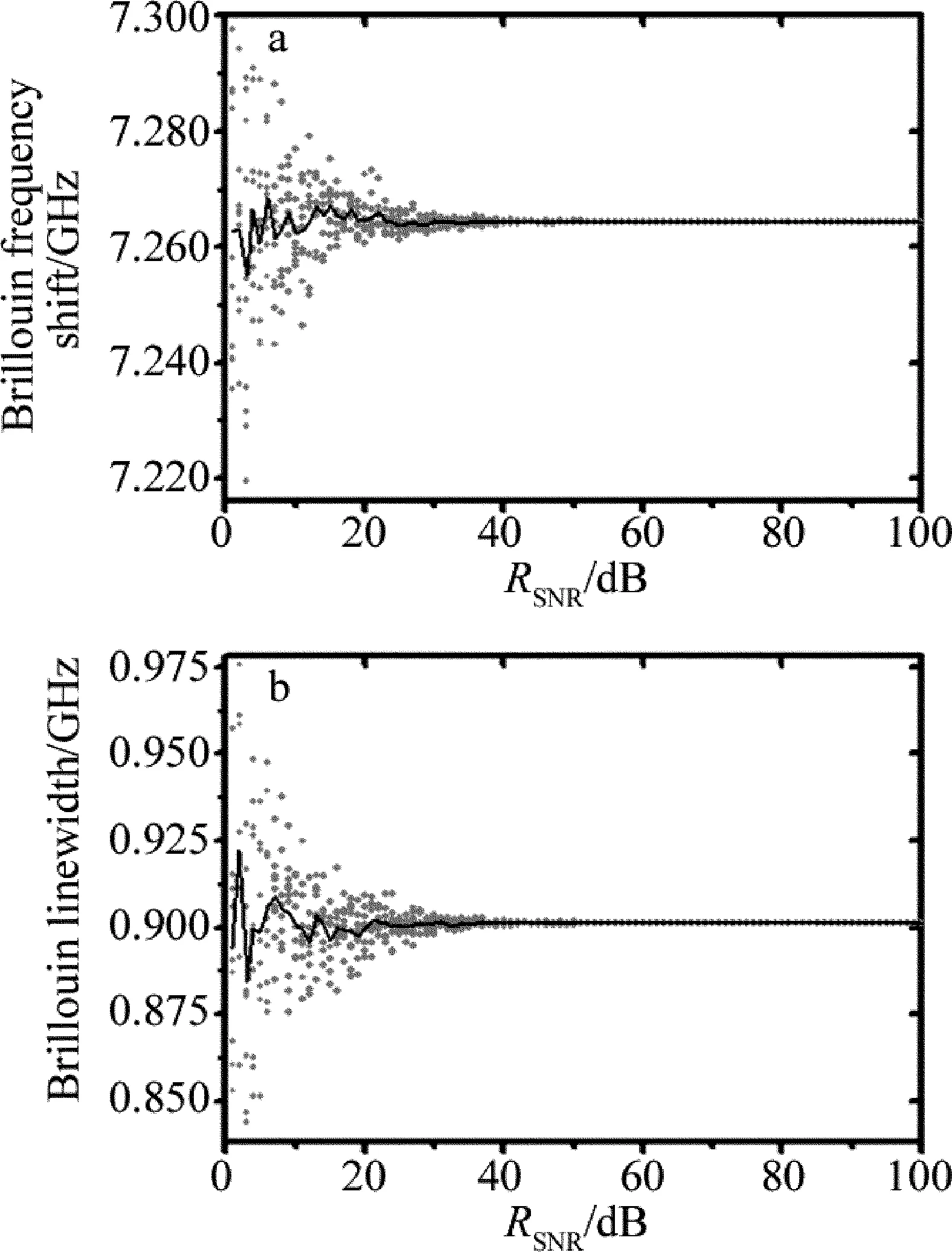
Fig.7a—the calculated frequency shift (dot) of each dB repeated 10 times withRSNRfrom 1dB to 100dB and their average values (dot-line)b—the calculated linewidth (dot) of each dB repeated 10 times withRSNRfrom 1dB to 100dB and their average values (dot-line)
由以上分析可以看出,单次测量受到RSNR的影响非常大,带来的误差达到几十到上百兆赫兹的误差。只有当谱线RSNR≥16dB时,单次测量温度才能达到0.2℃精度。而采用10次平均后,当RSNR≥ 7dB时,即可满足该温度测量精度。
3结论
讨论了布里渊激光雷达系统中ICCD上散粒噪声对海水布里渊散射频谱特征参量测量的影响。通过对SNR从1dB到100dB的仿真带噪布里渊谱进行仿真,并对每一个SNR进行100次的重复加噪和测量,发现散粒噪声的随机性会对布里渊频移和线宽的测量造成不确定性,进而对温度反演造成不确定性,该不确定性随着SNR的增大而减小,当SNR大于16dB时,频移和线宽的测量不确定度进入10MHz以内,带来的温度不确定度为0.2℃,此时的单次测量结果才能够满足高精度的测量要求。而考虑到实际应用中会进行多次测量取平均,讨论了10次平均后的散粒噪声对测量精度的提升情况。结果表明,10次平均能够使得该精度对谱线SNR的要求下降到7dB,这为以后的测量应用提供了一个理论参考。由于实验条件的限制,作者没有进行实际数据的分析,在以后的工作中,将结合实际数据对结果作进一步验证分析。
参考文献
[1]GAO W, LV Z W, DONG Y K,etal. A new approach to measure the ocean temperature using Brillouin lidar[J]. Chinese Optics Letters, 2006, 4(7): 428-431.
[2]XIE Z L, WANG Y M, WANG Q,etal. Inversion of seawater temperature based on variable Brillouin linewidth [J]. Laser Technology, 2012, 36(4):536-539(in Chinese).
[3]LIANG K, MA Y, CHEGN F,etal. Error analysis of measuring sea surface temperature based on brim detecting technology[J]. Opto-Electronic Engineering, 2008, 35(8):92-96(in Chinese).
[4]SCHORSTEIN K, POPESCU A, GOBEL M,etal. Remote water temperature measurements based on Brillouin scattering with a frequency doubled pulsed Yb∶doped fiber amplifier[J]. Sensors, 2008, 8(9):5820-5831.
[5]SHI J W, OUYANG M, GONG W P,etal. A Brillouin lidar sys-
tem using F-P etalon and ICCD for remote sensing of the ocean[J]. Applied Physics, 2008, B90(3/4): 569-571.
[6]LIU J, BAI J H, NI K,etal. Attenuation characteristics of laser beam in water[J]. Physics, 2007, 57(1):260-264(in Chinese).
[7]HE X D, XIA J, SHI J L,etal. Influences of effective gain length and attenuation coefficient on output energy of stimulated Brillouin scattering in water[J]. Physics, 2011, 60(5): 054207(in Chinese).
[8]LIANG K, MA Y, YU Y,etal. Research on simultaneous measurement of ocean temperature and salinity using Brillouin shift and linewidth[J]. Optical Engineering, 2012, 51(6): 066002.
[9]MA Y, YU Y, LI H,etal. Accurate measurement of high resolution spectrum obtained by F-P etalon and ICCD[J]. Applied Physics B, 2013:10.1007/s00340-013-5736-3.
[10]DUSSAULT D, HOESS P. Noise performance comparison of ICCD with CCD and EMCCD cameras[J]. Proceedings of the SPIE, 2004, 5563:195-204.
[11]LIANG K, MA Y, HUANG J,etal. Precise measurement of Brillouin scattering spectrum in the ocean using F-P etalon and ICCD[J]. Applied Physics, 2011, B105(2): 421-425.
[12]HUANG J, MA Y, ZHOU B,etal. Processing method of spectral measurement using F-P etalon and ICCD[J]. Optics Express, 2012, 20(17): 18568-18578.
Effect of random noise on oceanic Brillouin lidar measurement
WANGYuanqing1,HEJu2,MAYong1,YUYin1,ZHANGNian1,LIANGKun1
(1.Department of Electronics and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; 2. Wuhan National Laboratory for Optoelectronics, Huazhong Institute of Electro-Optics, Wuhan 430074, China)
Abstract:In order to analyze effect of random noise of lidar system on oceanic Brillouin scattering spectroscopy and temperature inversion precision, Brillouin scattering spectrum with noise was analyzed theoretically based on Brillouin scattering theory and system noise characteristics. Simulation experiment of signal-to-noise ratio (SNR) from 1dB to 100dB was conducted. The results showed that average error and uncertainty of frequency shift and linewidth can be controlled to the order of MHz when SNR is greater than 16dB. Temperature error and uncertainty can be controlled within 0.2℃. In actual application, the average of multiple measurements is taken. The average of 10 times can ensure the requirement of SNR is smaller than 7dB with measurement accuracy of 0.2℃. The study provides the guidance for lidar remote sensing precision in seawater.
Key words:laser technique; oceanic Brillouin scattering; random noise; frequency shift; linewidth; temperature; measurement error
收稿日期:2014-03-18;收到修改稿日期:2014-03-24
作者简介:王元庆(1989-),男,硕士研究生,现主要从事激光雷达在大气和海洋遥感方面的研究。
基金项目:国家自然科学基金资助项目(61108074)
中图分类号:TN247;TN958.98
文献标志码:A
doi:10.7510/jgjs.issn.1001-3806.2015.01.002
文章编号:1001-3806(2015)01-0006-07 1001-3806(2015)01-0013-06

