典型场景下电波传播特性建模

郭淑霞，单雄军，张 政，高 颖

(1.西北工业大学无人机特种技术重点实验室，西安710065;2.西北工业大学航海学院，西安710072)

对 Q

引 言

无论是雷达、卫星导航系统，还是电子对抗，都依赖于无线电波传输，避免不了对电波传播特性的分析。不能使用微扰、基尔霍夫法等传统方法来求解掠入射时粗糙的表面散射性能。近期有一些使用改进的算法来解掠入射问题的方法，能够定量分析掠入射多重散射特性，从而很好地求解大入射角散射系数问题［1］，但较难把大气波导影响加入其中;且需要利用积分数值法进行计算，计算量相当大［2］。利用抛物方程计算求解复杂大气条件，可应用于电波环境中。其中，阻抗边界条件可用混合傅里叶变换(mixed Fourier transform，MFT)处理，进而用离散混合傅里叶变换(discrete mixed Fourier transform，DMFT)实现。

中国电波研究所已对森林中的电磁波传播情况进行了实测和分析，并提出了经验模型。但是经验模型并不能准确预测地形与多径的传播特性影响［3］。LI等人对森林中的4层模型进行了研究［4］。然而，很难运用解析方法来分析森林与大气波导等电磁环境特性。

在森林电波环境分析中，对森林的电磁波的传播问题采用抛物方程进行求解，并且利用计算的结果和Tamir模型结果相互比较，证明抛物方程法在森林电波环境中可行性［5］。

采用抛物方程法对正常的大气分布、动态分析地海面情况下电波传播损耗的分析和计算，表明电波传播特性对特定环境中雷达和通信系统的正常工作产生重要的影响;但它未考虑粗糙表面及大气不均匀等因素的影响［6-8］。

基于抛物方程法分析粗糙海面上的电波传播特性，对于海面电波环境分析有较好的借鉴作用［9］。

以上仅考虑采用抛物方程法求解某一特定场景下电波传播损耗的问题。针对典型场景(如海上、山区、丘陵、城区)问题，无法使用已有典型场景下的基础模型来全面表达电波传播特性［10］。本文中建立一种适用于不同传输场景、基于确定性抛物方程的统一电波传播模型，可求解典型场景下的电波传播衰落问题。

1 典型场景分析

目前武器装备面临的场景主要有海上、山区、丘陵、城区，因此，这4个场景是本文中需要研究的典型场景。通过介电常数和电导率来划分武器装备所在的不同场景。当武器装备依次从海上、山区、丘陵、城区区域经过时，介电常数和电导率会发生变化，即抛物方程的边界条件发生变化，抛物方程的解相应发生改变。

针对本文中的典型场景，画出典型场景(海上、山区、丘陵、城区)的示意图，横坐标为区域，纵坐标为高度。如图1所示。

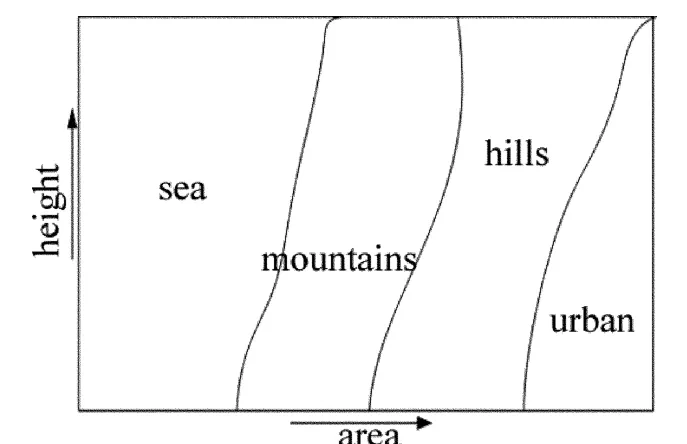
Fig.1 Schematic diagram of typical scenarios

以无人机为例。处于无人机的角度上，横坐标的区域表示无人机所在的区域，纵坐标的高度表示无人机远离研究对象的高度。假设无人机从海上、山区、丘陵、城区区域依次飞过时，通过介电常数和电导率的变化，即可得知无人机所在的区域。表1是典型场景下的介电常数和电导率的分布表。

Table 1 Dielectric constant and conductivity distribution under typical scenarios

已知典型场景下的介电常数和电导率，即可确定边界条件，运用统一电波传播模型可求得特定的解。得出仿真结果与相应的模型进行比较，验证统一电波传播模型的正确性。

2 基于抛物方程建立统一电波传播模型

电磁场谐因子是 e-iωt，其中，ω 为角频率，t为时间。所有电磁场分量和方位角都没有关系，方位角相互对称。方程在直角坐标系中可表示为:

式中，z为高度，x为距离，U为波函数，k为真空中的传播常数，n为折射指数。

根据微分算子理论对(1)式进行因式分解，可得:

式中，电波的前向传播对应前一个微分算子;电波的后向传播对应后一个微分算子，选取抛物方程的前向传播为研究对象，忽略后向传播的影响。得到近似抛物方程为:

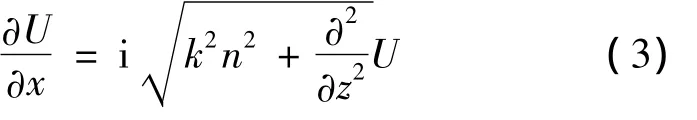
对 Q

用Fourier分步步进法求解窄角抛物方程(电波传播仰角小于15°)时，在x+Δx的场可似为:

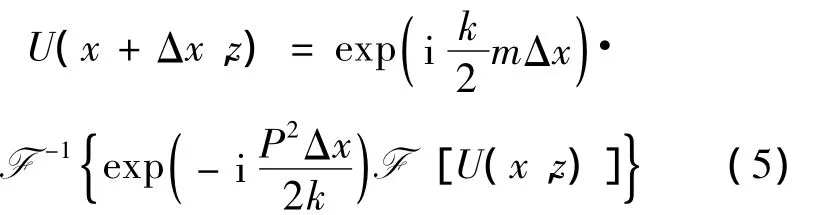
式中，m=n2-1+2z/ae，包含了地球曲率的影响，设地球的半径是ae为Fourier变换是相应的Fourier逆变换;P为Fourier变换的频域变量，通常P=ksinθ，θ为电波传播方向到水平方向的角度［11-12］。可以用合适的Fourier变换来表示其中的阻抗边界条件。

模型精度受电波传播仰角的影响比较大，当电波传播仰角大于15°时，应用窄角抛物方程建立的计算模型会产生较大误差。所以该模型合适的仰角小于15°。在推导方程解时，将场量进行分解，分解后结果为两个不同因子的乘积。根据以上理论，传播损耗L在数值上等于传播空间的传播损耗LBF与发射天线的空间发散损耗LPF之和。

式中，c为光速，d为传播距离，f为频率。

用分布步进法来求抛物方程(parabolic equations，PE)时，在相应的谱域中通过Fourier变换加入边界条件。对完纯导电平面，磁场或电场分别满足Neumann或Dirichlet的边界条件。通过镜像理论分析，边界条件的满足需边界有偶对称或奇对称。因此，Fourier变换可以变为单边余弦变换或正弦变换。

对导电的平面而言，电磁场的分量应满足Leontovich边界条件:

式中，

式中，Γ是边界Fresnel反射系数，θj是电波入射角。采用Fourier变换法求解满足阻抗边界条件(7)式的抛物方程时，通过引入混合Fourier变换就可满足边界条件，进而可以采用DMFT进行快速的求解。

基于PE建立统一电波传播模型，求解典型场景下电波传播衰落问题，即求解不同传输场景下抛物方程的边界条件问题。

分析典型的场景对电磁波传播的影响，可把典型的场景对应等效为损耗介质层［4，13］，并且用等效的反射系数ξ来表示:

式中，ε和σ分别是把典型的场景等效为损耗介质层的介电常数与电导率，λ为波长。

图2表明，在4种不同的水平传播距离(分别为10km，50km，100km和150km)情况下，电磁信号随高度变化的传播损耗。

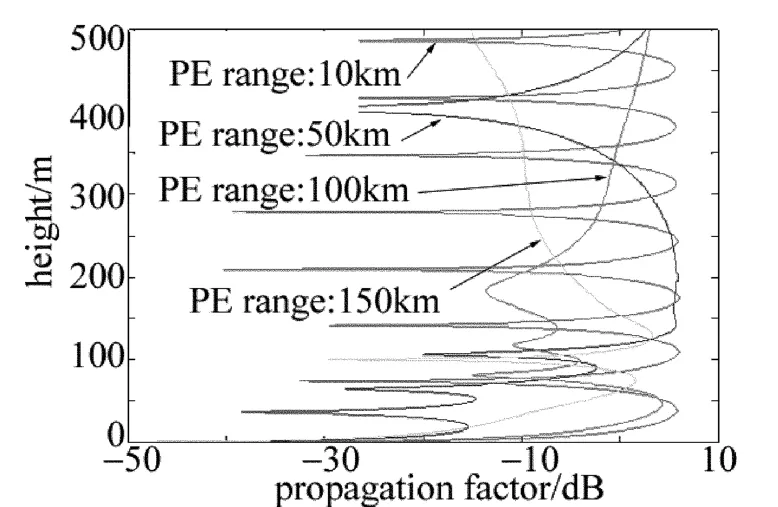
Fig.2 Attenuation characteristics of electromagnetic signal based PE equation

图3 表明采用水平极化方式，在不同距离及不同高度情况下，电磁信号传播随水平距离及高度变化的传播损耗。图中，蒸发波导高度为35m。不同的损耗值对应相应的颜色，可知传播损耗值随着距离增加而增大。

Fig.3 Signal propagation loss under horizontal polarization with different distance and different height

3 仿真分析

为了进一步验证统一电波传播模型的正确性，下面用统一电波传播模型计算典型场景下电波传播特性，并与相应的模型进行比较。

3．1 海上场景分析

假设海面上大气折射率为1、天线类型是高斯天线、发射天线水平极化、高30m、频率900MHz;海水介电常数为70、电导率为5S/m;最大传播距离为200km。用统一电波传播模型计算风速为10m/s的海面电波传播特性，距离为5km，海浪为中浪，浪高2.5m，海面的高度均方根差为0.63m，电波传播仰角小于15°。

图4显示传播因子随高度的变化，同时给出了Miller-Brown模型的结果。结果显示，两种方法结果较吻合，峰值与零点位置也一致。

Fig.4 Comparison between uniform radio propagation model and Miller-Brown model

此算例采用统一电波传播模型及阻抗边界条件的方法，仿真显示了统一电波传播模型能求解该问题。为验证统一电波传播模型的正确性，本文中计算了海面上的电波传播因子，并且和Miller-Brown模型相互的比较，二者能够很好地吻合。统一电波传播模型也可以分析海面的复杂电磁波环境和地形，而且也能分析复杂海洋环境的传播特性。

3．2 城区场景分析

以双射线模型作为基准参考模型，验证了统一电波传播模型的正确性。双射线模型的传播因子理论值为:

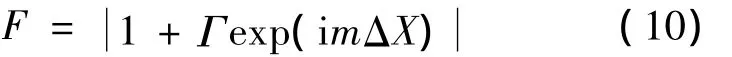
式中，ΔX为直射波与反射波的路程差，m为自由空间波数。

计算了一个简单小区内电波传播情况，其中，频率为900MHz，垂直极化的发射天线高度为5m，在小区内位于(41.8m，7.41m)处，长方体建筑尺寸为17m(长)×17m(宽)×24m(高)，街道的宽度为12m，接收点距发射天线的距离为850m，建筑表面的介电常数为4，电导率为0.05μS/m，电波传播仰角小于15°。采用统一电波传播模型的计算结果与射线追踪模型结果比较，如图5所示。

为了验证统一电波传播模型的正确性，此算例计算了城区建筑物上的电波传播因子，并与射线追踪法进行比较，二者吻合较好，验证了模型的正确性。这样的结果符合电波传播的物理机制。

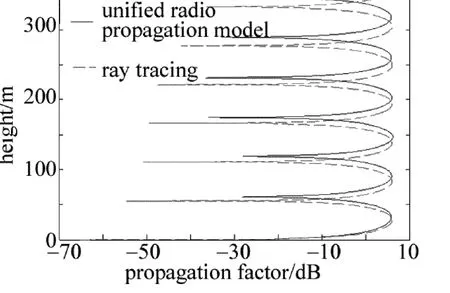
Fig.5 Comparison between uniform radio propagation model and ray tracing model

4 结束语

不同的电波传播场景需建立相应的传播模型，针对不同型场景问题，无法使用已有典型场景下的基础模型来全面表达电波传播特性。作者建立了一种适用于多传输场景、基于确定性抛物方程的统一电波传播模型，求解典型场景下的电波传播衰落问题，即求解不同边界条件下抛物方程的解。分析典型场景对电波传播的影响时，可把典型场景等效为损耗介质层，得到抛物方程的边界条件，进而可得到电波在典型场景下的传播损耗。在不同输场景下，将统一电波传播模型与Miller-Brown模型、射线追踪模型进行比较，结果较吻合，验证了其正确性。

［1］ HUAN Z G，TONG Ch M，HU G P.Study of low-grazing angle scattering effect from gaussian rough surface［J］.Electronics ＆ Information Technology，2007，29(2):482-485(in Chinese).

［2］ GUO J Y，WANG J Y，LONG Y L.Analysis of radio propagation over rough sea surface with parabolic equation［J］.Journal on Communications，2009，30(6):47-52(in Chinese).

［3］ GUO J Y，WANG J Y，LONG Y L.Analysis of radio propagation in partly forested terrain environment using parabolic equation approach［J］.Chinese Journal of Radio Science，2008，23(6):1045-1050(in Chinese).

［4］ LI L W，LEE Ch K，YEO T S，et al.Wave mode and path characteristics in a four-layered anisotropic forest environment［J］.IEEE Transactions on Antennas and Propagation，2004，52(9):2445-2455.

［5］ GUO J Y，WANG J Y，LONG Y L.Parabolic equation model for wave propagation in forest environments［J］.Chinese Journal of Radio Science，2007，22(6):1042-1046(in Chinese).

［6］ FENG K Sh，GE D B，LUO X Y，et al.Study on effects of the complex environment on radar and communication propagation with the method of parabolic equation［J］.Chinese Journal of Electronics，2000，28(6):68-71(in Chinese).

［7］ LI D X，YAN R J，GUAN W，et al.Research on two-way parabolic equation modeling under irregular terrain environment［J］.Journal of Astronautics，2012，33(2):235-241(in Chinese).

［8］ CHEN H F，CHEN Y，LI Y Y，et al.Simulation of atmospheric transmission characteristics of laser at 1.06μm［J］.Laser Technology，2014，38(2):266-269(in Chinese).

［9］ WANG Z L，FAN W Sh，ZHENG L H.Study and simulation on sea-surface propagation prediction model［J］.Chinese Journal of Radio Science，2008，23(6):1095-1099(in Chinese).

［10］ WANG K，YAN Y Q，LONG Y L，et al.Two-way parabolic equation approach for modeling radio wave propagation in the presence of multiple knife edges［J］.Chinese Journal of Radio Science，2011，26(6):1058-1064(in Chinese).

［11］ CAO S P，WANG W F，XUE X Ch.Dynamic 3-D shape measurement based on de-interlaced images by Fourier transform［J］.Laser Technology，2013，37(6):736-741(in Chinese).

［12］ MO X F，SHI J L，CHEN X G，et al.Measurement of SBS linewidth based on time-domain Fourier transform［J］.Laser Technology，2013，37(5):561-564(in Chinese).

［13］ HOLM P，LUNDBORG B，WAERN A.Parabolic equation technique in vegetation and urban environments［J］.IEEE Transactions on Antennas and Propagation，2003，32(3):464-468.